考虑多控制目标的IIDG低压穿越控制方法

何晋， 李智轩， 左金花， 李维希， 孙琮岳， 李光耀

(云南民族大学电气信息工程学院，云南 昆明 650031)

0 引言

随着新能源发电在电网中所占比重的不断增加，采用逆变器接口与电网相连的光伏、风电等逆变型分布式电源(inverter-interfaced distributed ge￣ne￣ra￣tors,IIDG)以其控制的高效性和灵活性等受到广泛的关注和应用[1—4]。在电网发生不对称故障时，若不对并网运行的IIDG采取合理的控制，将可能导致IIDG的大规模解列，严重影响电网运行安全。因此并网规程要求，IIDG应能在电网发生不对称故障时支撑电网电压，实现低压穿越运行[5—6]。

国内外学者对此进行了大量研究，文献[7—10]基于光伏、风电并网规程，提出正序分量控制法，在IIDG公共连接点(point of common coupling,PCC)电压跌落时，注入一定比例正序无功电流，但这一方法在三相电压不平衡度较高时的电压支撑效果较弱。文献[11]中提出正负序无功电流注入的电压支撑控制方法，但须对故障情况和IIDG出力情况进行运行场景划分，控制较为繁琐。文献[12]提出采用序列二次规划对所需正负序无功电流进行求解，但未考虑有功功率的控制。文献[13]提出正负序无功功率注入的电压支撑方法，同样未考虑有功功率输出控制。文献[14—15]提出了在αβ坐标系下，含系数分配的正负序分量控制方法，可有效提升PCC正序电压，降低三相电压不平衡度，同时考虑了故障时IIDG的有功功率输出，但未能给出有效的有功和无功功率参考值计算方法。文献[16]在实现有功和无功功率的灵活调节时，有效解决了变流器过流问题。文献[17]提出一种IIDG有功功率控制方法，但故障时，IIDG应优先向电网注入无功功率。文献[18—19]分析了不对称故障下对IIDG有功和无功功率振荡抑制的控制，实现有功和无功振荡抑制的灵活控制，但未考虑IIDG的电压支撑控制。文献[20—21]提出一种动态调整正负序电压参考值的正负序无功电流注入方法，虽然电压支撑效果较好，但未考虑有功输出振荡抑制控制。

分析上述文献可知，目前针对IIDG的低压穿越控制或是单独考虑电压支撑和电流限幅控制，或是只考虑有功和无功功率振荡抑制控制，控制策略均存在一定缺陷。因此文中提出一种考虑多控制目标的IIDG低压穿越控制方法，实现了电网发生不对称故障时IIDG的电压支撑控制、有功输出振荡抑制控制，最大有功功率输出和电流限幅控制这3个控制目标，有效提升了IIDG的运行稳定性。最后在PSCAD/EMTDC中搭建仿真模型，验证了该控制策略的可行性。

1 不对称故障下IIDG输出特性

图1为IIDG并网结构拓扑，由DG发电单元、直流升压电路、逆变电路、LC滤波器构成。PWM为脉宽调制；Vdc为直流母线电压；Rf,Lf，Cf分别为LC滤波器的等效电阻、电感和电容；Rg，Lg分别为电网线路等效电阻和电感；iabc，Vabc分别为PCC电流和电压相量；mabc为PWM调制波信号；vg为电网侧电压相量；PDG为IIDG发电单元输出功率。

图1 IIDG并网拓扑Fig.1 IIDG grid-connected topology

当电网侧出现短路故障或是突然接入不对称大容量负载时将会导致IIDG的并网点电压出现不对称跌落。对于电网中任意不对称故障，PCC处电压相量在αβ坐标下由正负序分量可表示为式(1)。考虑到IIDG多并入三相三线制配电网运行，故下文分析中忽略零序分量[5]。

(1)

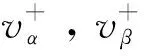
(2)

进一步将式(1)中的正负序电压分量进行Park变换，可得到正负序电压dq分量为：

(3)

同理，对式(2)中正负序电流分量进行Park变换，可得到正负序电流dq分量为：

(4)

由图1所示网络结构可列出PCC电压与电网侧电压vg在αβ坐标系下的关系为：

(5)

将式(1),式(2)和式(4)代入式(5),可得到电压支撑幅值为：

(6)

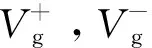
图2 电流内环控制框图Fig.2 The block diagram of the current inner loop control

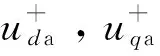
2 IIDG电压支撑控制

在IIDG容量充足和电网线路阻抗并不是特别小的情况下，通过对IIDG输出电流进行合理的控制，PCC三相电压幅值可较为准确地控制在限定电压范围内，确保不出现过电压或电压低于限值的情况。同时做出2点假设：(1) 电网线路阻抗Zg已知；(2) 电网侧电压vg已知。实际上Zg和vg可利用电网阻抗检测技术获得[25]，但计算Zg和vg不是讨论重点，故假设这2个值为已知条件。根据并网规程规定，设定相电压上、下限值Vset，max，Vset，min分别为1.1 p.u.和0.9 p.u.。因此电压支撑控制应满足以下约束条件：

(7)

在电压不对称跌落情况下，PCC三相电压幅值可表示为：

(8)

式中：Va，Vb，Vc分别为PCC三相电压幅值；相角φ=φ+-φ-，为正负序电压相量初相角差，其值可由下式求出：

(9)

由式(8)可定义不对称电压跌落时PCC三相电压幅值最大和最小值为：

(10)

其中：

(11)

根据式(7)的相电压约束条件，可定义正负序电压参考限值Vref，max和Vref，min为：

(12)

将式(12)中Vref，max和Vref，min反代入式(10)，替换式(10)中的Vmax和Vmin即可求解得出正负序电压参考值为：

(13)

其中：

(14)

将式(13)所求的正负序电压参考值代入电压支撑方程式(6)中，即可求出实现电压支撑目标所需的正负序电流参考值，其计算如下：

(15)

由上式同样可以得到上文分析中的结论，即在Xg>>Rg时，有功电流分量几乎不起电压支撑作用，电压支撑完全由无功电流分量实现。但当线路电阻不能被忽略时，有功电流分量也将起到电压支撑作用，电压支撑控制框图如图3所示。

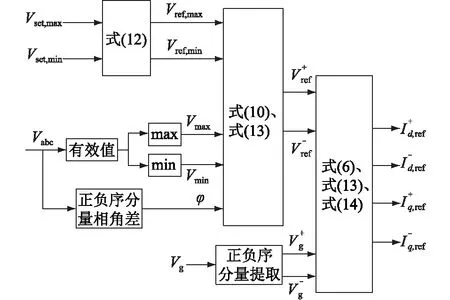
图3 电压支撑控制框图Fig.3 The block diagram of voltage support control

在感性网络条件下，为实现有功输出振荡抑制控制和最大有功功率输出和电流限幅控制，需要对负序无功电流分量和正序有功电流分量进行额外的控制。

3 有功输出振荡抑制控制

在电网发生不对称故障期间，IIDG将向电网注入负序电流。这将导致IIDG的瞬时有功功率输出出现二倍频波动，同时有功输出中的倍频分量将使得IIDG直流侧母线电压出现波动，影响系统运行安全。直流母线电压振荡峰值和有功输出振荡峰值之间的关系如下[19]：

(16)

不对称故障时，IIDG的瞬时有功功率为：

(17)

其中：

(18)

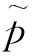
(19)

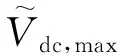
(20)

4 最大有功功率输出和电流限幅控制

(21)

其中：

(22)

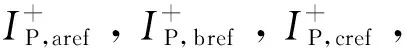
(23)

由此即获得了实现最大有功功率输出的正序有功电流参考值，同时可将IIDG输出的三相电流幅值控制在Iset，max内。感性网络条件下的多目标低压穿越控制框图如图4所示。

图4 感性条件下多目标低压穿越控制框图Fig.4 The block diagram of multi-target low voltage ride-through control under perceptual conditions

5 仿真算例验证

为了验证上文所述控制策略的可行性，同时对比传统低压穿越控制，根据图1所示IIDG并网结构图，搭建仿真测试平台。为了还原不对称故障时IIDG所采用不同控制策略对直流母线电压的影响，IIDG发电单元采用光伏发电模型[25]。考虑到不对称故障持续时间较短，故设定为恒定光照和温度条件，而最大功率点追踪控制(maximum power point tracker，MPPT)采用恒定电压观察法来实现。仿真测试一共设置3个测试案例，主要为验证以下3点：(1) 文中控制方法与传统正序无功电流注入控制方法在感性网络条件下的电压支撑控制效果对比；(2) 在感性网络下，电压支撑控制和有功输出振荡抑制控制之间的关系；(3) 文中所提低压穿越控制在阻感性网络条件下的电压支撑效果。系统参数和测试参数如表1所示。

表1 系统参数和测试参数Table 1 The system parameters and test parameters

5.1 算例1：电压支撑控制对比传统正序无功电流注入控制

本算例目的是对比文中控制方法与传统正序无功电流注入法面对不对称故障时的电压支撑效果，线路阻抗设置为Zg=j0.3 Ω。设置在仿真0.5 s时电网发生不对称故障，故障共持续1 s，在1.5 s时切除故障，故障期间共发生5种不同情况的电压跌落,网侧电压跌落情形如图5所示。

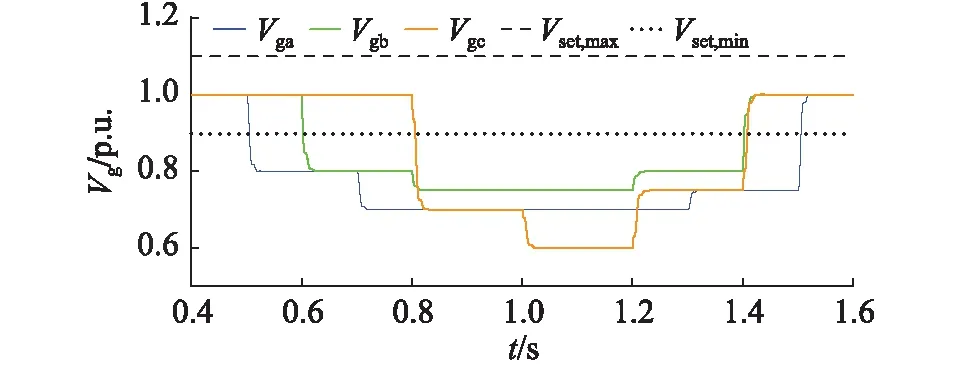
图5 网侧三相电压幅值Fig.5 Grid-side three-phase voltage amplitude

仿真结果如图6—图10所示，其中0.5～1.0 s为电压支撑控制结合有功功率振荡抑制控制作用结果，在1.0 s投入最大有功功率输出和电流限幅控制。

图6 PCC三相电压幅值(算例1)Fig.6 Three-phase voltage amplitude of PCC (example 1)

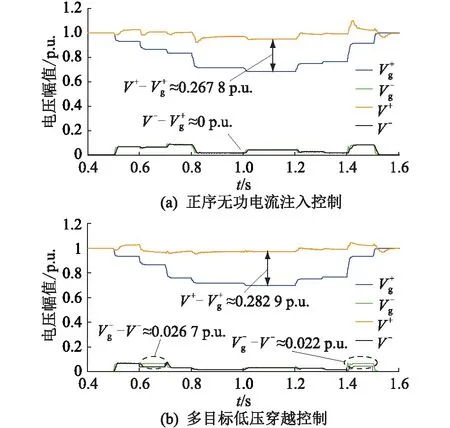
图7 PCC与Vg正负序电压幅值(算例1 )Fig.7 Positive and negative sequence voltage amplitude of PCC and Vg(example 1)

图8 PCC三相电流(算例1)Fig.8 Three-phase current of PCC (example 1 )

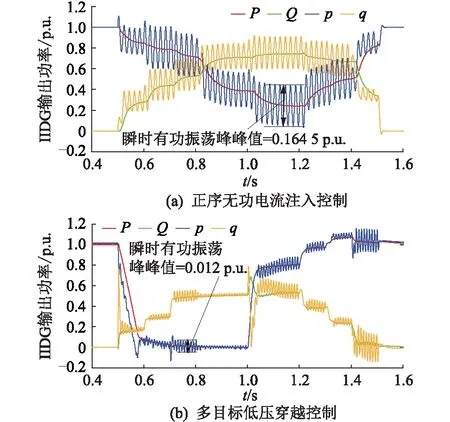
图9 IIDG输出功率(算例1)Fig.9 Output power of IIDG (example 1)

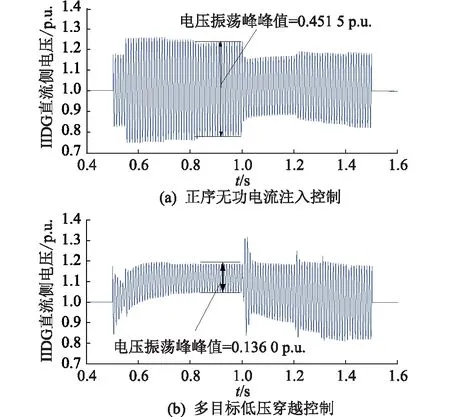
图10 IIDG直流母线电压(算例1)Fig.10 DC bus voltage of IIDG (example 1)

由图6(a)可以看到，正序无功电流注入控制在0.5～1.5 s故障期间，出现多处电压越出限值范围的情况；对比图6(b)可知，在多目标低压穿越控制策略的控制下，PCC三相电压幅值较为准确地被控制在限值范围内。忽略暂态过程，主要对比稳态控制效果，可以看出，文中所提多目标低压穿越控制较传统正序无功电流注入控制有更好的电压支撑效果。

根据图7对比2个控制的正序电压幅值提升程度和负序电压幅值降低程度。由图7(a)可以看到，正序无功电流注入控制将PCC正序电压幅值较网侧正序电压幅值提升了0.267 8 p.u.，但PCC负序电压幅值与网侧负序电压幅值差值近似为0;而由图7(b)可以看到，文中所提控制将PCC正序电压幅值较网侧正序电压幅值提升了0.282 9 p.u.，同时负序电压幅值在2个取样点分别减少了0.026 7 p.u.和0.022 p.u.。由此可以看到文中所提控制可有效提升PCC正序电压，同时减小三相电压不平衡度。

由图8(a)、(b)可知，2种控制方法均能有效地将IIDG输出的三相电流控制在限值范围内，且由图8(b)可以看到，在1.0 s时投入最大有功功率输出和电流限幅控制后，IIDG输出的三相电流立即抬升至1.1 p.u.，仿真结果与理论分析一致。

由图9(a)可以看到在正序无功电流注入控制的作用下，IIDG的瞬时有功功率p和无功功率q输出出现了较大程度的波动，其中取样点处瞬时有功功率振荡峰峰值为0.164 5 p.u.。与图9(b)对比可以看到，在有功输出振荡抑制控制的作用下，IIDG的瞬时有功和无功功率输出波动程度明显较小，在取样点处瞬时有功振荡峰峰值仅为0.012 p.u.。同时也可以看到在1.0 s最大有功功率输出和电流限幅控制投入后，瞬时有功功率输出从0 p.u.抬升至0.8 p.u.附近，与理论分析一致。

同理分析图10，由图10(a)可以看到，在正序无功电流注入控制的作用下IIDG直流侧母线电压出现了较大的波动，在取样点处的电压振荡峰峰值为0.451 5 p.u.，而由图10(b)可知，在文中所提控制方法作用下，取样点处的电压振荡峰峰值仅为0.136 0 p.u.，IIDG直流母线电压振荡程度较小。

综合上述分析可知，对比传统正序无功电流注入，文中所提多目标低压穿越控制方法在电压支撑控制、有功输出振荡抑制控制和最大有功功率输出控制方面具有更好的控制效果。

5.2 算例2：电压支撑控制结合有功输出振荡抑制控制

前文对电压支撑控制和有功输出振荡抑制控制之间的关系进行了理论分析，本算例对此进行验证，此时线路阻抗设置为Zg=j0.3 Ω。设置ab两相电压跌落故障，故障设置在0.4 s发生，故障持续时间0.4 s，前0.2 s控制为电压支撑控制加最大有功功率输出控制，0.6 s时投入有功输出振荡抑制控制，且控制考虑以有功输出振荡抑制为第一控制目标，设定有功振荡峰峰值的限值为0.15 p.u.，仿真结果如图11—图14所示。

图11 PCC与Vg三相电压幅值(算例2 )Fig.11 Three-phase voltage amplitude of PCC and Vg(example 2)

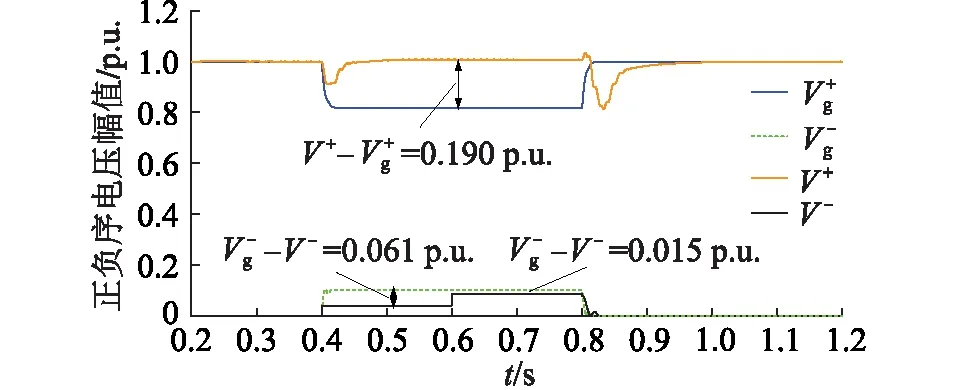
图12 PCC与Vg正负序电压幅值(算例2)Fig.12 Positive and negative sequence voltage amplitude of PCC and Vg(example 2)

图13 PCC三相电流(算例2)Fig.13 Three-phase current of PCC (example 2)

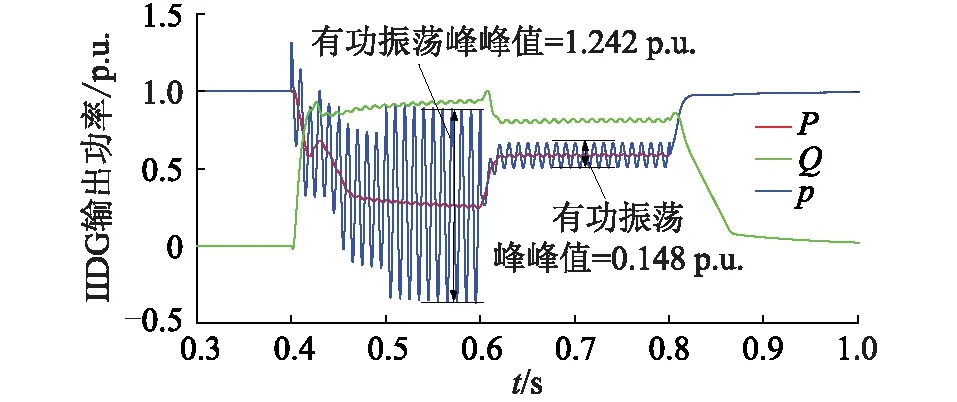
图14 IIDG输出功率(算例2)Fig.14 Output power of IIDG (example 2)

由图11可知，在0.4～0.6 s，PCC三相电压幅值在故障稳态被较好地控制在限值范围内，在0.6 s，有功输出振荡抑制控制投入后，PCC处c相和b相电压幅值略微超出限值，仿真结果符合理论分析。

分析图12可知，在电压支撑控制的作用下PCC正序电压幅值较网侧电压幅值提升了0.190 p.u.。同时可以看到，在0.4～0.6 s，PCC处和网侧负序电压差值为0.061 p.u.，0.6 s有功振荡抑制控制投入后，负序电压差值减小为0.015 p.u.，这是由于有功输出振荡抑制控制的投入减小了IIDG输出的负序无功电流，使得PCC负序电压幅值上升。仿真结果符合理论分析。

由图13可知,IIDG输出的三相电流均被控制在限值范围内。进一步分析图14可知，0.4～0.6 s期间，IIDG瞬时有功功率输出出现了较大振荡，其中取样点处的有功振荡峰峰值为1.242 p.u.，在有功输出振荡抑制控制投入后，瞬时有功功率振荡程度明显减小，其中取样点处的有功振荡峰峰值仅为0.148 p.u.，小于设定的有功振荡峰峰值限值。此外还可以看到，在0.6 s时有功输出振荡抑制控制投入后，IIDG无功功率输出略微减小，而有功功率输出略微上升，这是因为IIDG注入的负序无功电流减小，导致整的无功输出减小，同时多出的容量则转换为有功功率注入电网。综上所述，仿真结果符合理论分析结果，验证了电压支撑控制和有功输出振荡抑制控制之间的关系。

5.3 算例3：阻感性网络条件下电压支撑控制

本算例目的为验证电压支撑控制在阻感性网络条件下(R/X=1)电压支撑的效果，此时线路阻抗设置为Zg=0.21+j0.21 Ω。设置仿真0.4 s时发生故障，共持续0.7 s，在1.1 s时切除故障，期间设置发生6种不同的电压跌落情形。仿真结果如图15—图18所示。由图15可见，PCC三相电压幅值被较为良好地控制在限值范围内。由图16可见，PCC处正序电压幅值较网侧正序电压幅值在取样点处提升了0.137 p.u.，同时PCC处负序电压幅值较网侧负序电压幅值在取样点处减小了0.03 p.u.。

图15 PCC与Vg三相电压幅值(算例3)Fig.15 Three-phase voltage amplitude of PCC and Vg (example 3)

图16 PCC与Vg正负序电压幅值(算例3)Fig.16 Positive and negative sequence voltage amplitude of PCC and Vg(example 3)

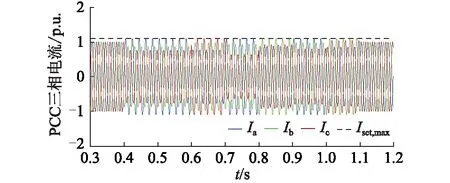
图17 PCC三相电流(算例3)Fig.17 Three-phase current of PCC (example 3)

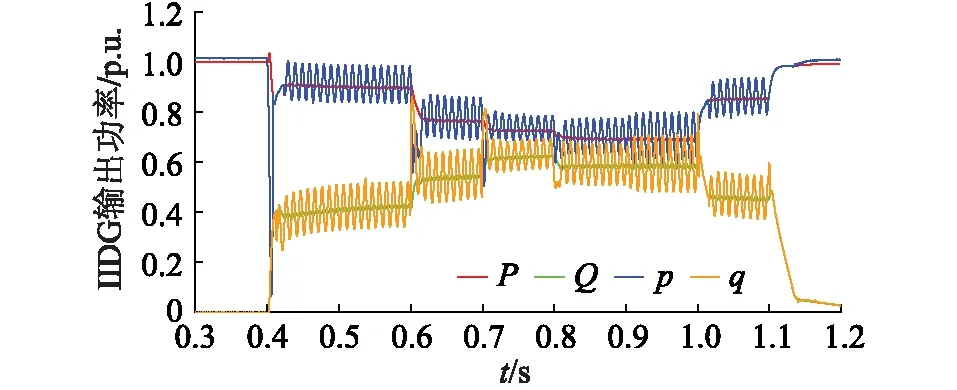
图18 IIDG输出功率(算例3 )Fig.18 Output power of IIDG (example 3)

由图17可知，IIDG输出的三相电流均被控制在限值范围内。在之前的测试中，电网被设定为感性网络，电压支撑控制只通过注入无功电流实现电压支撑目标，在算例3中，根据式(15)分析可知，在电网为阻感性时，电压支撑控制通过注入正负序有功和无功电流实现电压支撑，因此由图18可知，有功和无功功率被同时输出注入电网。综上分析可知，仿真结果符合理论分析。

6 结语

针对目前IIDG低压穿越控制存在的电压支撑效果不理想，控制目标单一等缺陷，提出一种考虑多控制目标的IIDG低压穿越控制，通过控制IIDG向电网注入合适比例的正负序有功和无功电流，分别实现以下控制目标：(1) 任意阻感性网络条件下的电压支撑，确保PCC三相电压幅值可较好地控制约束在电压范围内；(2) 感性网络条件下有功输出振荡抑制控制，有效抑制有功输出出现的波动，提升系统运行稳定性；(3) 最大有功功率输出和电流限幅控制，充分利用IIDG的剩余容量。

本文得到云南省教育厅科学研究基金项目(2021Y654)资助，谨此致谢！