HFMI 处理的钢制焊接接头疲劳评估模型探讨

胡鑫，李艳青，黄进浩

(中国船舶科学研究中心,深海载人装备国家重点实验室,无锡,214082)

0 序言

为解决焊接结构对整体结构在循环载荷下的疲劳寿命的削弱问题[1-3]，通常需要对焊接结构进行焊后处理，以改善焊缝拐角处切口形状并引入压缩残余应力.当前常见的焊后处理技术有：锤击、打磨、非熔化极气体保护焊(tungsten insert gas welding,TIG 焊)熔修以及高频机械冲击(high frequency mechanical impact，HFMI)等，其中HFMI 以可靠、有效、易操作的特点在工程领域备受青睐.技术的发展也助推HFMI 的手段的多样化，包括高频冲击、超声喷丸、超声速冲击、气动冲击等[4].

目前国内外对于HFMI 处理的钢制焊接接头疲劳试验和评估两个方向的研究取得了一定的进展.Deguchi 等人[5]对经超声速冲击处理后的焊接接头疲劳强度进行试验研究，结果表明处理后的焊接接头疲劳S-N曲线相较于未处理接头具有更低的倾斜度，因此小应力范围下疲劳寿命的提升更为显著，同时利用超声喷丸处理在疲劳寿命上获得的获益与应力比相关.Yildirim 等人[6]通过对应力比R=0.1、承受轴向疲劳载荷的3 种焊接接头形式、共计228 个数据点的综合性分析发现，经高频冲击处理后的接头疲劳强度随着材料屈服强度的增加而增加，并推荐材料静屈服强度每增加200 MPa，则疲劳等级FAT 增加12.5%(视为增加一个疲劳等级).Wang 等人[7]对几种经超声喷丸处理后的接头疲劳强度开展试验研究，基于名义应力系统，推荐S-N曲线斜度取为10，并拟合出了Q235B 材料的接头疲劳等级FAT 与应力比R之间的线性方程.上述试验研究均集中于单轴疲劳方向.针对HFMI处理的钢制接头的疲劳评估，一般做法是将材料屈服强度划分若干个区间，赋予每个区间不同的FAT值[4,6,8].然而，其至少存在两点不足：①忽略了应力比对疲劳寿命的影响；②由于推荐FAT 值的“跳跃性”，这种疲劳评估方法将会有一定的偏差，尤其当材料屈服强度处于区间的左右边界时，偏差将更为显著.鉴于此，广泛选取了经HFMI 处理的接头疲劳试验数据，接头材料具有不同的屈服强度，试验在不同应力比条件下开展.将缺口应力法与SWT(smith-watson-topper)与Walker 两种精度较高的平均应力修正模型相结合，并采用ABAQUS 有限元软件对试验数据进行了重新分析，提出了能同时考虑不同屈服强度和应力比的疲劳评估模型，具有一定的工程实际应用价值.

1 缺口应力法与平均应力修正模型

1.1 缺口应力法

缺口应力法是源于Radaj 等人[9]提出的微观支持理论，即焊趾(或焊根)局部范围内的平均应力是影响焊接接头疲劳的主要因素.为了便于分析，一般采取在缺口处构建一个半径为 ρf的圆弧，如图1 所示.基于线弹性理论，用圆弧段上应力最大值代表微结构约束长度范围内的应力平均值.虚拟半径 ρf满足式(1).

图1 虚拟圆弧定义Fig.1 Definition of fictitious notch rounding

式中：ρ为结构实际缺口半径；S为约束因子；ρ*为微结构约束长度.

理论上虚拟半径的取值与诸多因素有关，为了便于实际的应用，国际焊接学会推荐了统一化的取值方案[10]：板厚t≥5 mm 时，虚拟半径 ρf取1 mm；板厚t＜5 mm 时，虚拟半径 ρf取0.5 mm，以避免造成接头承载能力出现过度削弱.

相比于名义应力法与热点应力法，缺口应力法考虑除焊趾(或焊根)实际缺口外所有的局部焊接特征对疲劳强度的影响，包括焊趾倾角、焊接错边、焊缝轮廓、尺寸效应等，因而评估精度较高.与此同时，该评估方法仅用一条S-N曲线就可以评估所有种类焊接接头的疲劳寿命.

1.2 SWT 模型与Walker 模型

一般认为，拉应力会加速裂纹的萌生与扩展，而压应力则相反.因此，相同的应力幅作用下，应力比R越大，则疲劳寿命越小.为了预测不同R下结构疲劳寿命，几种评估模型相继被提出，其中SWT 模型与Walker 模型评估精度较高.两种评估模型形式如下.

SWT 模型为

Walker 模型为

式中：σar为疲劳损伤参量；σmax为循环加载时应力最大值；σa为循环加载时应力幅值；γ为材料相关参数，其值越小，表示材料对平均应力越敏感.

2 试验数据选取与分析

2.1 数据选取

鉴于材料屈服强度fy与应力比R对HFMI 处理的焊接接头疲劳寿命均有明显影响，在选择试验数据时遵循两个基本原则：①焊接接头的材料多样化；②同一材料的焊接接头需在不同的应力比下开展试验.在此基础上，选取的经HFMI 处理后的焊接接头疲劳试验包含120 个疲劳试验数据点，材料屈服强度fy在272～ 719 MPa 之间，应力比R在-1～ 0.5 范围内.试验基本信息统计如表1 所示.

表1 试验基本信息Table 1 Basic information of fatigue tests

2.2 名义应力系统下试验数据分析

图2 为表1 中5 组试验的名义应力疲劳试验数据.从图2 可以看出，应力比R越大，疲劳寿命越短；材料屈服强度fy越高，疲劳寿命越长，这与焊后未处理接头(as-welded)疲劳寿命特点表现出明显差异.

图2 名义应力疲劳试验数据Fig.2 Nominal stress test data.(a) cruciform joints;(b)longitudinal fillet joints;(c) butt joints

为了更进一步描述HFMI 处理接头疲劳寿命与R以及fy三者之间的关系，注意到各组试验均含有R=0.1 与R=0.5(其中Wang 等人[11]的试验中用R=0.45 的数据点近似代替R=0.5)这两种工况，这为分析R与fy对疲劳寿命的影响创造了条件.按照以下3 个步骤对各组数据进行分析工作.

(1)提取R=0.1(R=0.5)下各组试验数据点，明确名义应力范围Δσ与R的对应关系.

(2)各组试验数据点逐一进行线性回归分析，得到存活率PS=50%的S-N曲线，获取相应的疲劳等级FAT(循环次数N=2×106次所对应应力范围).

(3)将得到的FAT 值和相对应的屈服强度fy作为一个新的数据点，并将这些数据点再做一次回归分析，进而得到FAT 与fy的关系式.

图3 为FAT，R，fy三者之间的关系，并可以用方程(4)描述.

图3 不同R 与fy 下的疲劳等级Fig.3 Fatigue level with different R and fy values

式中：M(R)为与应力比R有关的参数.当R=0.1时，M(R)可取为190 MPa；当R=0.5 时，M(R)可取为120 MPa.

3 缺口应力系统下的疲劳评估

3.1 有限元模型

利用ABAQUS 2018 软件进行有限元建模，模型全部采用二次六面体单元.沿着焊接接头的表面与靠近焊趾的方向，网格密度逐渐增大.由于所有试件板厚均大于5 mm，故采用1mm 的虚拟半径.根据国际焊接学会关于网格划分的推荐[10]，需保证焊缝局部区域网格小于0.25 mm，模型网格划分情况如图4 所示，非承载式角焊缝接头焊趾焊根处有限元划分细节如图5 所示.依据试验中的试样夹紧及加载位置对有限元模型施加约束与载荷，基于线弹性理论进行有限元分析,并采用最大主应力强度准则进行疲劳评估.

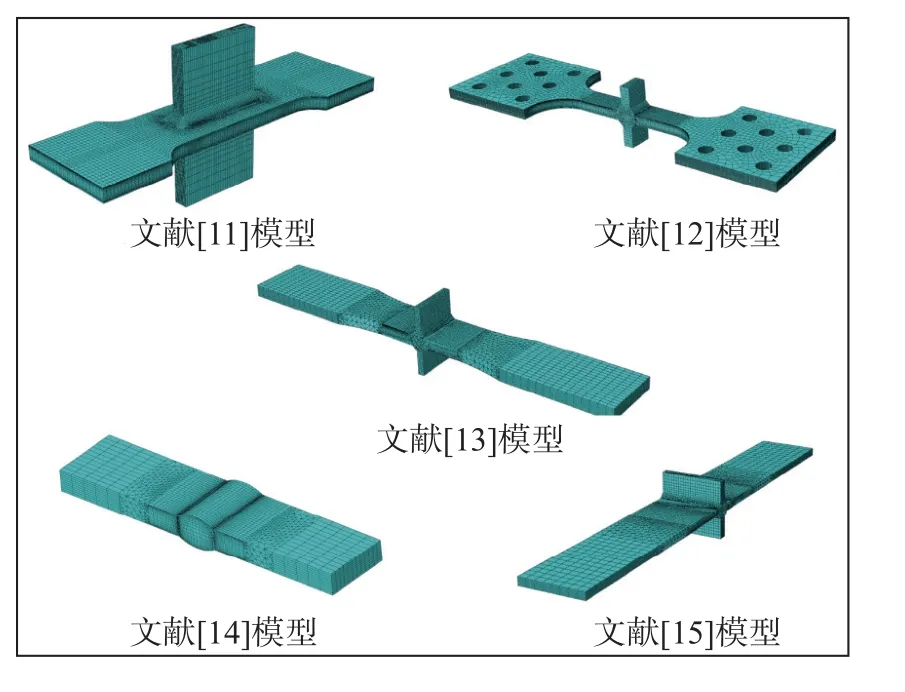
图4 有限元模型Fig.4 Finite element models

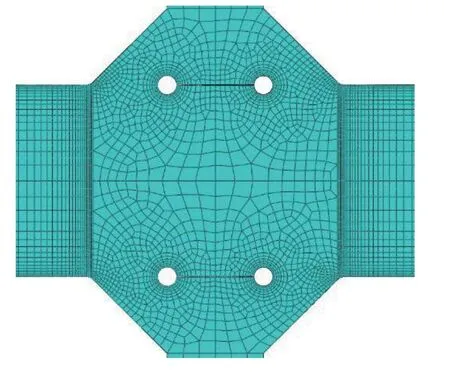
图5 非承载式角焊缝接头划分细节Fig.5 Mesh details for unloaded fillet joints

有限元计算结果如表2 所示，其中对于对接接头，考虑到其在焊接过程中容易产生焊接错边，对计算结果乘以1.1 的修正系数.

表2 有限元计算结果Table 2 Finite element results

结合图2 中名义应力数据，利用式(5)和式(6)得到循环加载时缺口应力系统下的两个应力参量.

式中：σmax为循环加载应力最大值；σa为循环加载应力幅值；Δσn为循环加载名义应力范围.

结合式(2)、式(5)和式(6)可以得到SWT 模型的疲劳损伤参量而Walker 模型的疲劳损伤参量的取值关键在于参数γ，其值可通过以下方法来确定.

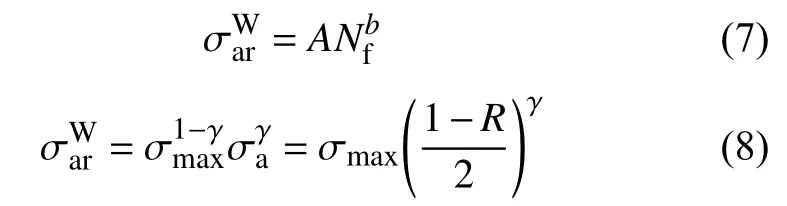
式中：Nf为疲劳寿命；A与b均是通过试验数据在对数坐标系下拟合确定的参数.

结合式(7)和式(8)可得式(9).

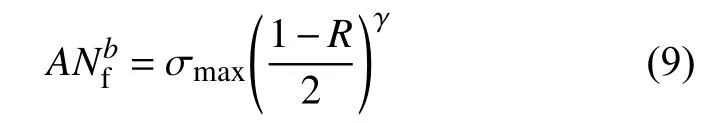
对式(9)左右两边取对数可得式(10).

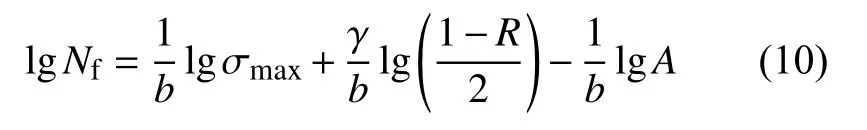
3.2 疲劳评估结果

图6～ 图9 为基于缺口应力法的SWT 模型与Walker 模型的试验数据点分布情况，对各组试验数据点进行线性回归分析，分别计算得到存活率PS=97.7%/50%/2.3%的疲劳评估S-N曲线以及数据分散带带宽Tσ，其是衡量数据点离散性的一个重要参数.Tσ表达式为

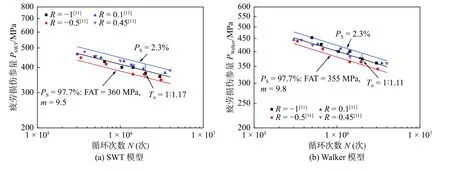
图6 文献[11]试验疲劳评估结果Fig.6 Fatigue assessment results of reference[11].(a) SWT model;(b) Walker model

图7 文献[12-13]试验疲劳评估结果Fig.7 Fatigue assessment results of reference[12-13].(a) SWT model;(b) Walker model

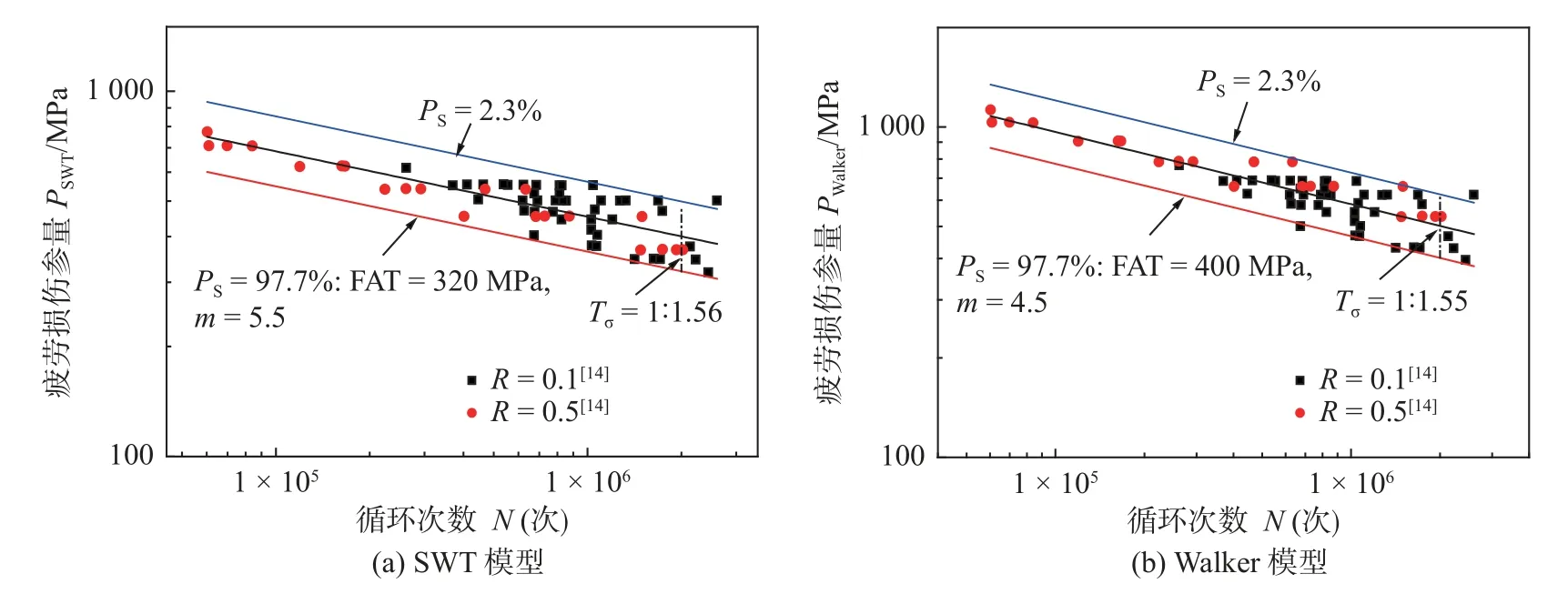
图8 文献[14]试验疲劳评估结果Fig.8 Fatigue assessment results of of reference[14].(a) SWT model;(b) Walker model

图9 文献[15]试验疲劳评估结果Fig.9 Fatigue assessment results of of reference[15].(a) SWT model;(b) Walker model

表3 为SWT 模型与Walker 模型评估结果.表3 的分析结果呈现4 个特征：①与名义应力系统相比，无论是SWT 模型还是Walker 模型，各组试验不同应力比下的数据点分布未出现明显的分层，同时分散带带宽较窄，数据点离散性较好；②相较SWT 模型，Walker 模型分析的数据分散带更窄，因此利用该模型得到的S-N曲线进行疲劳评估的精度较高；③Walker 模型中的参量γ因材料而异(有研究认为γ与材料屈服强度有关，相关关系仍尚不明确，表3 中γ与fy也没有明显相关关系)；④无论哪种模型，材料不一致时，分析得到的S-N曲线斜度m也不同(从目前数据分析的结果上看m随着屈服强度fy增大而减小).鉴于以上4 个特征可以推断，使用Walker 模型进行评估的前提条件是被研究对象的母材需要有相同材料制成的接头疲劳试验数据作为支撑.当需要评估的钢制焊接接头缺乏同种材料接头的疲劳数据时，考虑到SWT 模型形式固定，将所有试验数据点利用SWT 模型置于一个分析系统中，得到如图10 所示的评估结果.从图10 可以看出，不同R与不同fy的数据点分布没有出现明显分层，这意味着该模型能综合反映二者对疲劳寿命的影响.经线性回归分析后，得到存活率PS=97.7%的S-N曲线，其FAT=325 MPa，斜度m=6.5.

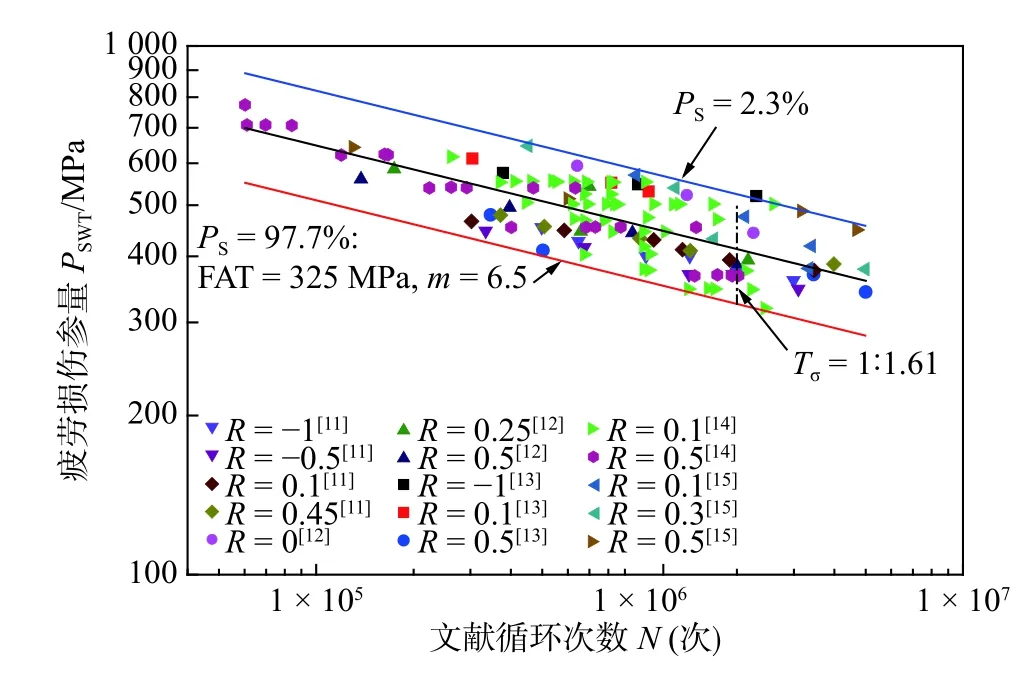
图10 SWT 模型下试验数据点评估结果Fig.10 Fatigue assessment results based on SWT model

表3 SWT 模型与Walker 模型评估结果Table 3 SWT model and Walker model evaluation results

4 结论

(1)经HFMI 处理的钢制焊接接头的疲劳寿命与应力比R、材料屈服强度fy有很强的相关性，更小的应力比和更高的屈服强度将具有更长的疲劳寿命.名义应力系统下，疲劳等级FAT 与R，fy三者之间可以近似用关系式FAT=0.1fy+M(R)来描述，M(R)是与R有关的参数.

(2)当被研究对象的母材有相同材料制成的接头疲劳试验数据作为支撑时，可以使用精度较高的Walker 模型并结合缺口应力法进行评估.

(3) SWT 模型疲劳损伤参量形式固定，能综合反映应力比R与屈服强度fy对疲劳寿命的影响，线性回归得到了SWT 模型下存活率PS=97.7%的S-N曲线，其FAT=325 MPa，斜度m=6.5，用该SN曲线进行疲劳评估时不限制被研究对象的加载应力比和母材材料的屈服强度.