The First Photometric Analysis of Two Low Mass Ratio Totally Eclipsing Contact Binaries:TIC 393943031 and TIC 89428764

Yan-Ke Tang ,Ya-Ni Guo ,Kai Li ,Ning Gai ,and Zhi-Kai Li

1 College of Physics and Electronic Information,Dezhou University,Dezhou 253023,China

2 Shandong Provincial Key Laboratory of Optical Astronomy and Solar-Terrestrial Environment,Institute of Space Sciences,Shandong University,Weihai 264209,China;yanierguo@163.com

Abstract Photometric analysis of the contact binaries TIC 393943031 and TIC 89428764 was carried out using Transiting Exoplanet Survey Satellite and SuperWASP data for the first time.Using the Wilson–Devinney code,we have found that TIC 393943031 is a low-mass-ratio deep contact binary with a fillout factor of 50.9(±1)% and a mass ratio of q=0.163±0.001.TIC 89428764 is a medium and low-mass-ratio contact binary with a fillout factor of 34.5(±1)%and a mass ratio of q=0.147±0.001.Furthermore,the period study reveals both the stars exhibit continuously increasing periods,the increasing rate is 4.21×10-7 day yr-1 for TIC 393943031 while 6.36×10-7 day yr-1 for TIC 89428764.The possible reason is mass transfer from the secondary component to the primary component for both stars.Meanwhile,we discussed their evolutionary phases and orbital angular momenta.

Key words:Stars–(stars:) binaries:eclipsing–stars:low-mass

1.Introduction

Contact binaries surrounded by a common envelope are predominantly active systems that show interaction between both primary and secondary components.According to Binnendijk (1970,1977),contact binaries can be divided into A-subtype and W-subtype binaries.A-subtype binaries refer to the systems that the more massive stars have higher temperature,on the contrary,the less massive stars are hotter for W-subtype binaries.Contact binaries are speculated that they may have evolved from detached binaries through angular momentum loss via magnetic braking (Guinan &Bradstreet 1988;Bradstreet &Guinan 1994;Qian et al.2017).Contact binaries with mass ratio less than 0.25 and fillout factor more than 50%are called deep low mass ratio contact binaries(Qian et al.2005a,2006;Yang &Qian 2015).They may be the bridge between binary stars and single stars,and may evolve into fast rotating single stars,such as blue stragglers,when the mass ratio is lower than the critical mass ratio (Rasio 1995;Qian et al.2005b;Arbutina 2007;Jiang et al.2010;Zhu et al.2016).However,many of the details of the evolution of contact binaries are not clear,for example,period cut-off(Rucinski 1992;Weldrake et al.2004;Li et al.2019b),the thermal relaxation oscillation theory (Flannery 1976;Lucy 1976).Solving these problems requires us to study much more contact binaries.

Excellent photometric data are provided by Transiting Exoplanet Survey Satellite (TESS) (Ricker et al.2014,2015),which was launched in 2018,and performing a near all-sky survey for planets.Moreover,its excellent photometric precision,combined with its fine time sampling and long intervals of uninterrupted observations,enables searching for low mass ratio contact binaries.Meanwhile,the mass ratio of the contact binaries can be reliably obtained from the totally eclipsing light curves (Pribulla et al.2003;Terrell &Wilson 2005;Li et al.2019a,2021).

TIC 393943031 and TIC 89428764 are two totally eclipsing contact binaries which were first discovered by Pojmanski(2002).He pointed out that both of them were contact binaries,and their Vmag,period,amplitude variation in V-band were 10.9 mag,0.44978 day,0.4 mag for TIC 393943031,while 10.2 mag,0.37660 day,0.33 mag for TIC 89428764.After that,Lohr et al.(2015) regained their periods and gave the period variation rates for the first time.The values of periods wererespectively.The rates of period variation were 5.88×10-7and 8.80×10-7day yr-1.In this paper,their photometric solutions were carried out for the first time.Combining the TESS and SuperWASP data,we reanalyzed their orbital period changes.

2.Observations

2.1.TESS Observations

We used the Simple Aperture Photometry (SAP)light curve and Pre Data Search Conditioning SAP light curves of TESS from the Mikulski Archive for Space Telescopes in this paper.We downloaded the light curves from sector 2 and sector 28 of TESS for TIC 393943031 and TIC 89428764.The time span is from BJD 2458354 to BJD 2459087 for TIC 393943031,while from BJD 2458325 to BJD 2459084 for TIC 89428764.The data included 2 minutes cadence and 10 minutes cadence.

The Generalized Lomb–Scargle periodogram (Zechmeister&Kürster 2009) method is employed to calculate the periods.Figure 1 shows the power spectra of the orbital periods of TIC 393943031 and TIC 89428764.In the figure and sub-figure,the maximum peaks marked with black dashed lines are corresponding to the half value of orbital period.The derived periods are 0.449941 day for TIC 393943031 and 0.376610 day for TIC 89428764,respectively.In Section 3,both of the periods are corrected according to the O-C analysis.The corrected value is 0.449797 day for TIC 393943031,while the value stays the same for TIC 89428764.

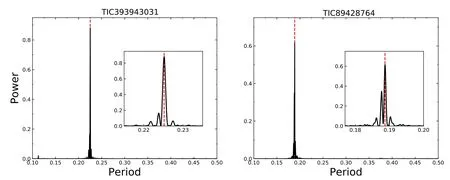
Figure 1.The power spectra of period about TIC 393943031 and TIC 89428764 calculated by GLS.The insert box is an enlarged figure around the peaks,and the red dotted lines represent the peak values.

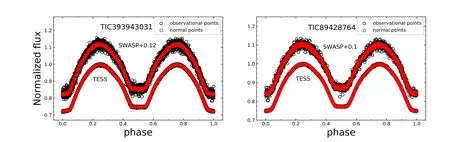
Figure 2.The phase-fold light curves of TIC 393943031 and TIC 89428764,which are folded with the corrected period.The black hollow circles represent observational points,and the red hollow circles represent the normal data.

All the time domain light curves are folded to phase ones according to the corrected periods,and are shown in Figure 2.In order to obtain the photometric solutions quickly,the observational data are combined into 1000 normal points,and these normal points are weighted according to the number of the observations during the following light-curve synthesis.The observational points and normal points are shown in Figure 2.The black circles in the figure display the observational points,while the red ones show the normal points.As seen in the figure,the two sets of light curves are completely consistent.

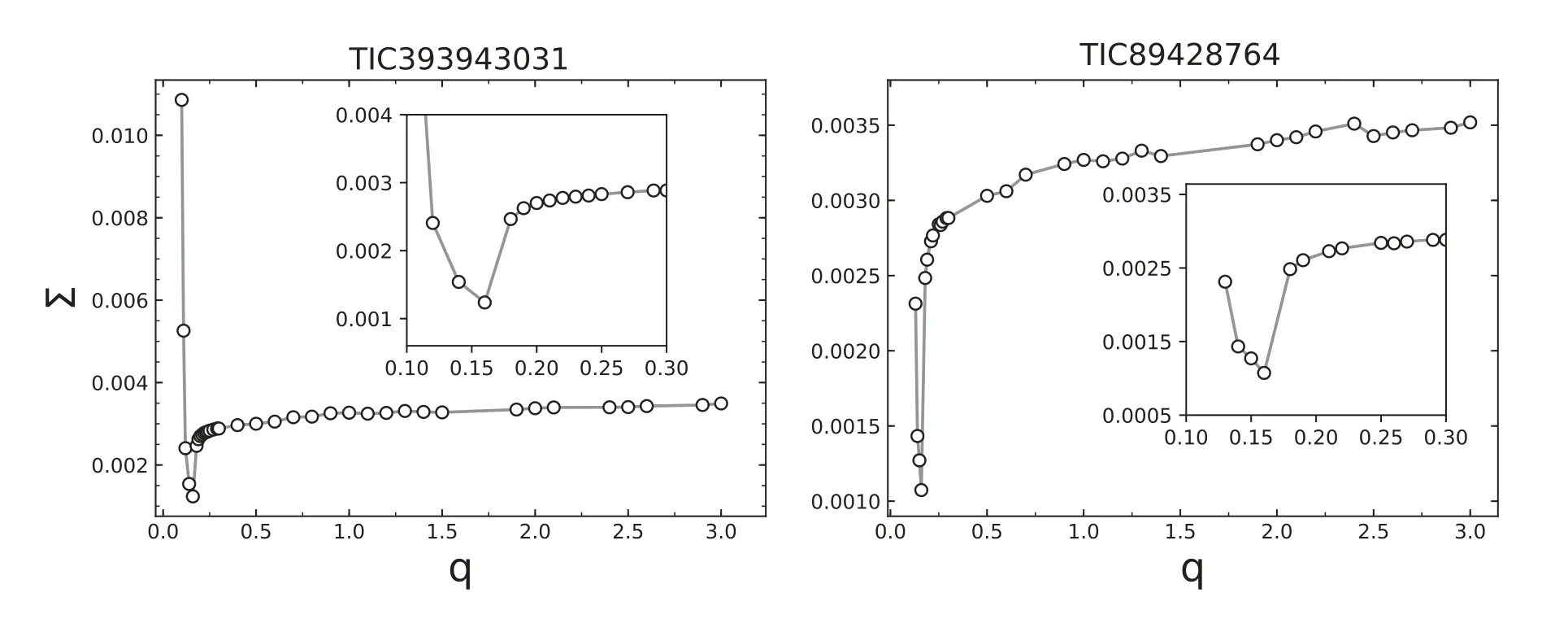
Figure 3.The q-search figures.The “q” represents mass ratio.The “∑” refers to sum squares of residuals.

2.2.SuperWASP Observations

Meanwhile,we download all the data of the two targets from SuperWASP (Butters et al.2010).The time span is from BJD 2453862 to 2456998 for TIC 393943031 and from BJD 2453862 to 2456972 for TIC 89428764.All the data are used to calculate the minima and some high-precision data are selected to obtain the photometric solution.The data observed by camera ID:221 and 222 of TIC 393943031 and camera ID:222 of TIC 89428764 were selected to obtained the photometric solution.

According to the corrected periods,the SuperWASP time domain light curves are folded to phase ones.Then we apply a 1σ limit to exclude the bad-points in SuperWASP data using Gaussian processes (Bishop 2006;Rasmussen &Williams 2006).After exclude the bad-points,the observational points are combined into 1000 normal points,and these normal points are also weighted according to the number of the observations during the following light-curve synthesis.The observational data and the normal ones are displayed in Figure 2.

3.Photometric Solutions

The Wilson–Devinney(W-D)program(Wilson&Devinney 1971;Wilson 1979,1990) was used to simultaneously model the weighted light curves of TESS and SuperWASP.The primary effective temperatures were estimated by color index,and the mean temperatures were adopted as the temperatures of primary stars.The details are listed in Table 1.In the processing,the value of E(B-V) and the interstellar extinctions of different filters were obtained according to Green et al.(2018).Then,the corresponding temperatures were determined according to Pecaut &Mamajek (2013) of B-V,g′ -i′,and the one of J-K was obtained based on Covey et al.(2007).According to Table 1,the mean temperatures are set to the primary temperatures,6430 K for TIC 393943031 and 7030 K for TIC 89428764.The gravity-darkening coefficients and the bolometric albedos were g1,2=0.32 according to Lucy(1967)and A1,2=0.5 according to Ruciński(1969),and the bolometric and bandpass limb-darkening coefficients were from van Hamme (1993)'s table.

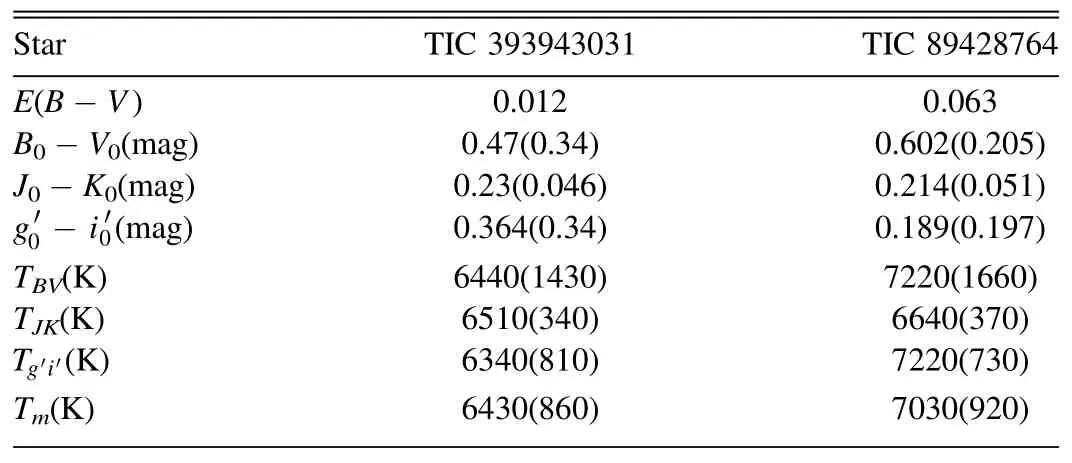
Table 1 Temperatures of TIC 393943031 and TIC 89428764

Mass ratio is a significant parameter for obtaining a credible photometric solution.Due to lack of the spectral observation,we adopted the q-search method to determine the mass ratio.The value of sum squares of residuals will return each time when the mass ratio changes.Finally,the value corresponding to the minimum sum squares of residuals was adopted as the initial mass ratio,and as an adjust parameter input into the W-D code.The q-search result is shown in Figure 3.

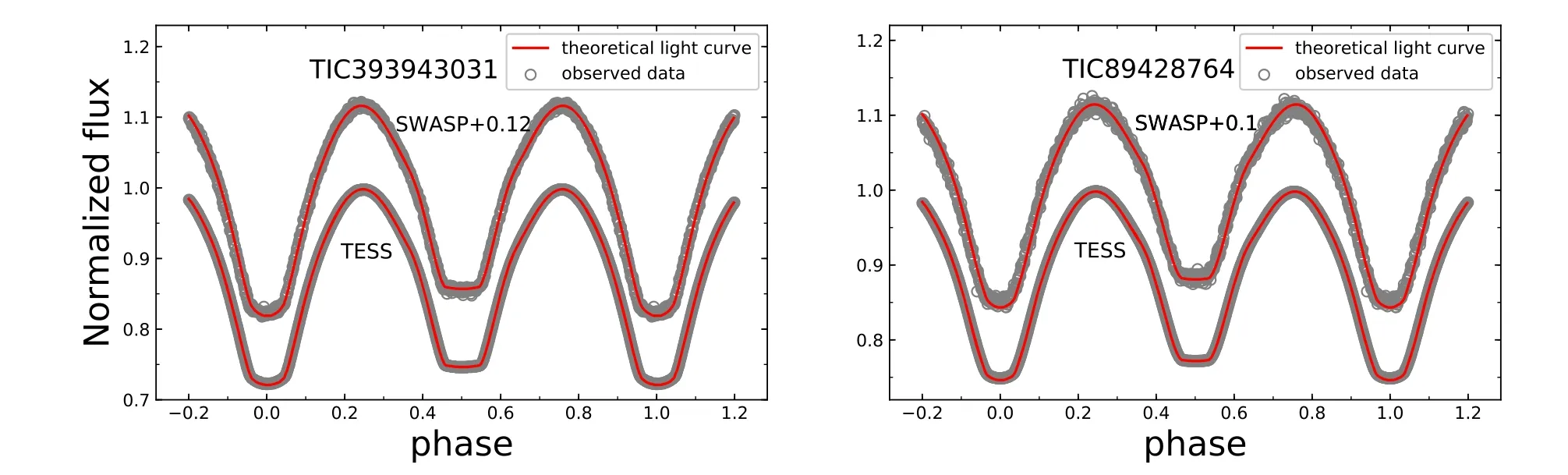
Figure 4.The fitting light curves of TIC 393943031 and TIC 89428764.The observed data are normal data.The “SWASP” refers to SuperWASP data.

In fact,the mean temperatures estimated by color index are the average values of the primary and secondary stars,and cannot be regarded as the primary temperatures,strictly.So the correction was carried on after obtained the radius ratio k=r2/r1and the temperature ratio T2/T1.The temperatures of the primary and secondary stars can be determined according to the following equation (Zwitter et al.2003;Christopoulou &Papageorgiou 2013):

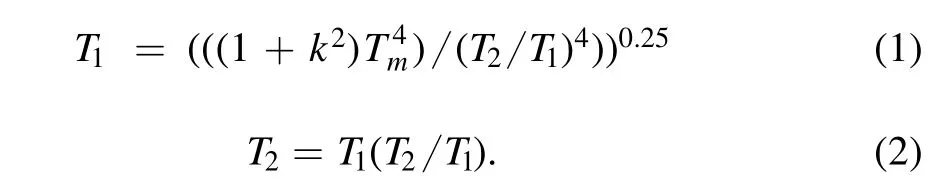
The primary temperatures calculated by the above equations are set as fixed parameters in the process of the re-running W-D code,while the temperatures of secondary stars are set as the adjusted parameters.The final photometric solutions are shown in Table 2.The fitting light curves are shown in Figure 4.The uncertainties of primary and secondary stars were obtained through the error propagation of Tm.The errors of the other parameters in Table 4 are not real but formal ones,and they are underestimated (Prša &Zwitter 2005).We can see the observed light curves and theoretical light curves of both targets display a very high degree of coincidence.

4.Orbital Period Investigations

4.1.TIC 393943031

The data of TESS and SuperWASP were used to calculate minima according to the K-W method (Kwee &van Woerden 1956).There are totally 366 minima,151 from SuperWASP and 215 from TESS.The minima are listed Table 3.The O-C method was applied to analyze period variation.“O”refers to the observation minimum,while“C”is the value of calculation.In this processing,the initial linear ephemeris is as follows:

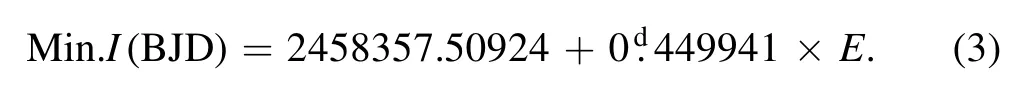
According to Equation (3),O-C values were obtained and shown in the left panel of Figure 5.From the figure,we can see the data in the rectangle,showing an obvious linear variation.It is most likely due to the inaccuracy of the period.Therefore,a linear fit was used to this part of data.The fitting result is shown in the right panel of Figure 5.The linear equation is:

According to Equation(4),the O-C values were recalculated and listed in Table 3.Then we used the least square method to fit the O-C values.The fitting result is shown in the left panel of Figure 6.The fitting equation is as follows:In the figure,we can see that the period shows a long-term increasing trend.From Equation (5),the period increasing rate can be calculated as dP/dt=4.21×10-7day yr-1.

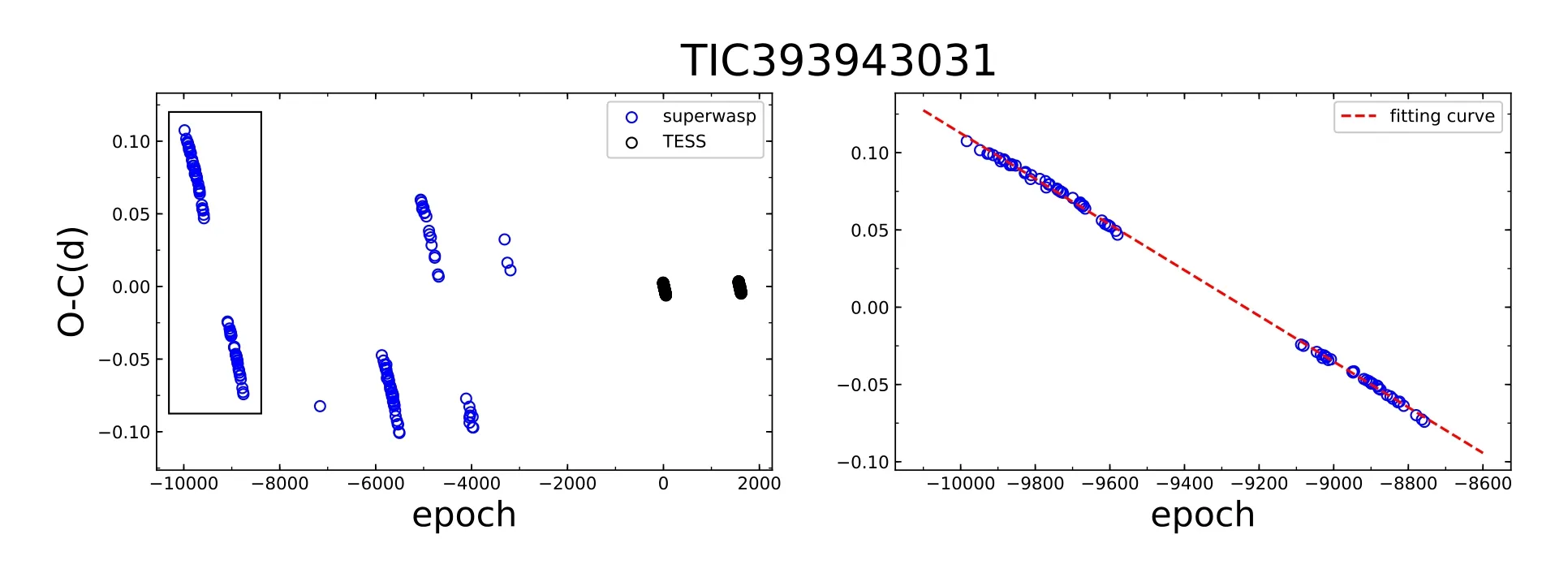
Figure 5.The left panel is the O-C values of TIC 393943031 calculated by the period of GLS.The right one is the linear fitting light curve of the data circled by the rectangle in the left panel.

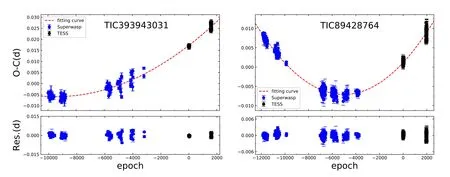
Figure 6.The O-C values and the fitting light curves of TIC 393943031 and TIC 89428764.

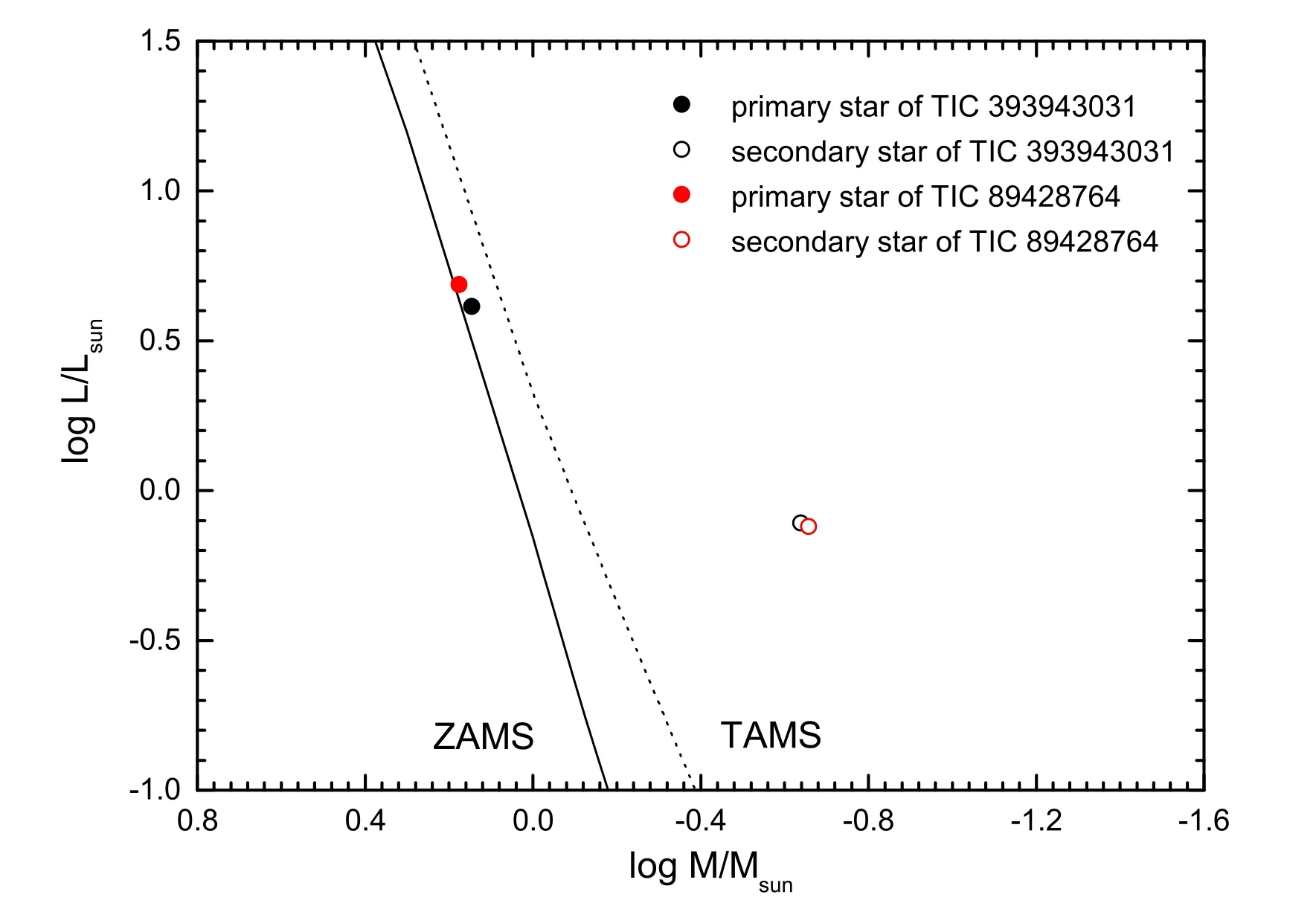
Figure 7.This figure displays the M-L diagram of TIC 393943031 and TIC 89428764.

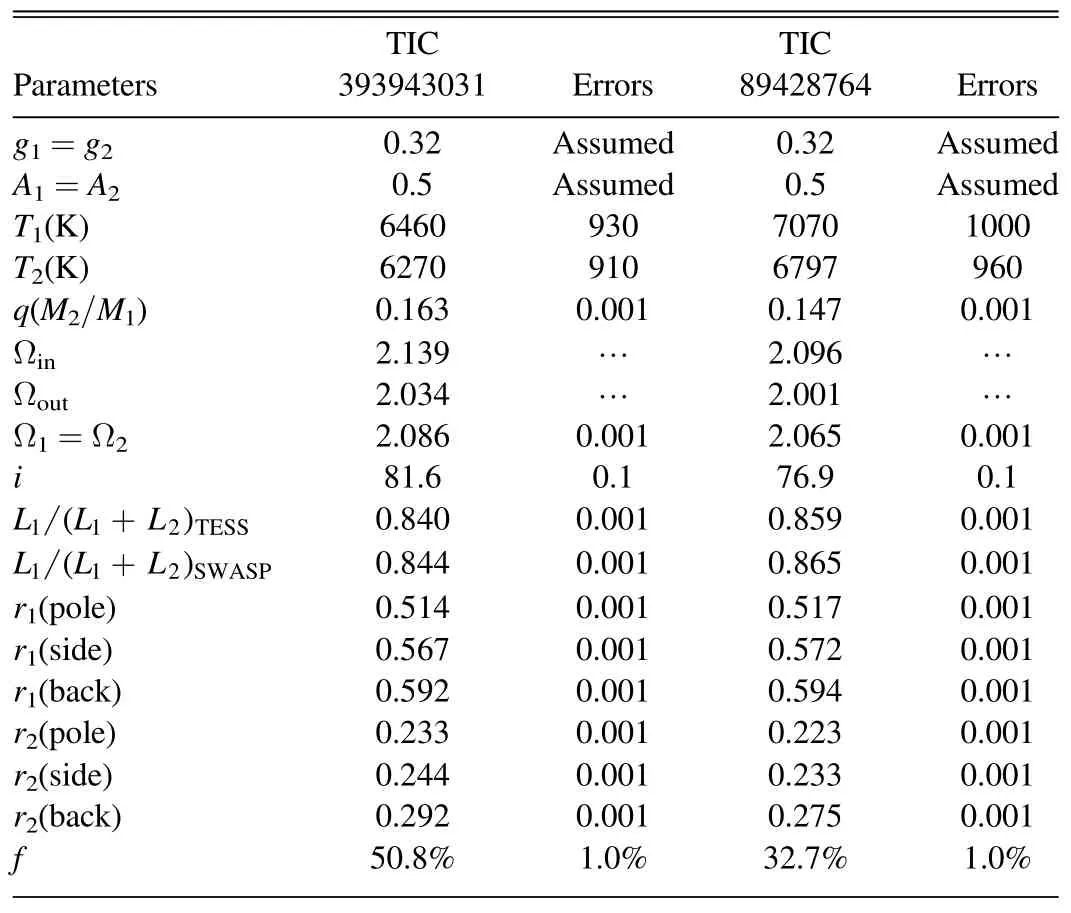
Table 2 Photometric Results of TIC 393943031 and TIC 89428764

4.2.TIC 89428764

All the minima of TIC 89428764 were calculated,including 225 minima from SuperWASP and 225 minima from TESS.To obtain the details of the period variation of TIC 89428764,the O-C values were calculated.The linear ephemeris used to calculate the O-C values is:

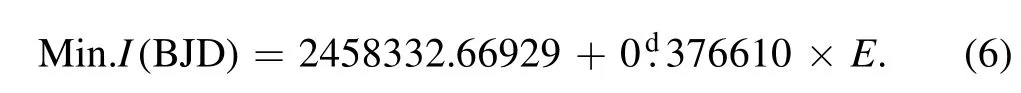
The minima and corresponding O-C values are listed in Table 4.In order to quantify the period variation,the least square method was used for fitting the O-C values.The fitting equation is

Table 3 The Minimum Moments of TIC 393943031

Table 4 The Minimum Moments of TIC 89428764

The right panel of Figure 6 shows the O-C values and the fitting curve.The bottom is residuals of the fitting.From Figure 6,TIC 89428764 shows a long increasing period variation,and the rate is dP/dt=6.36×10-7day yr-1.

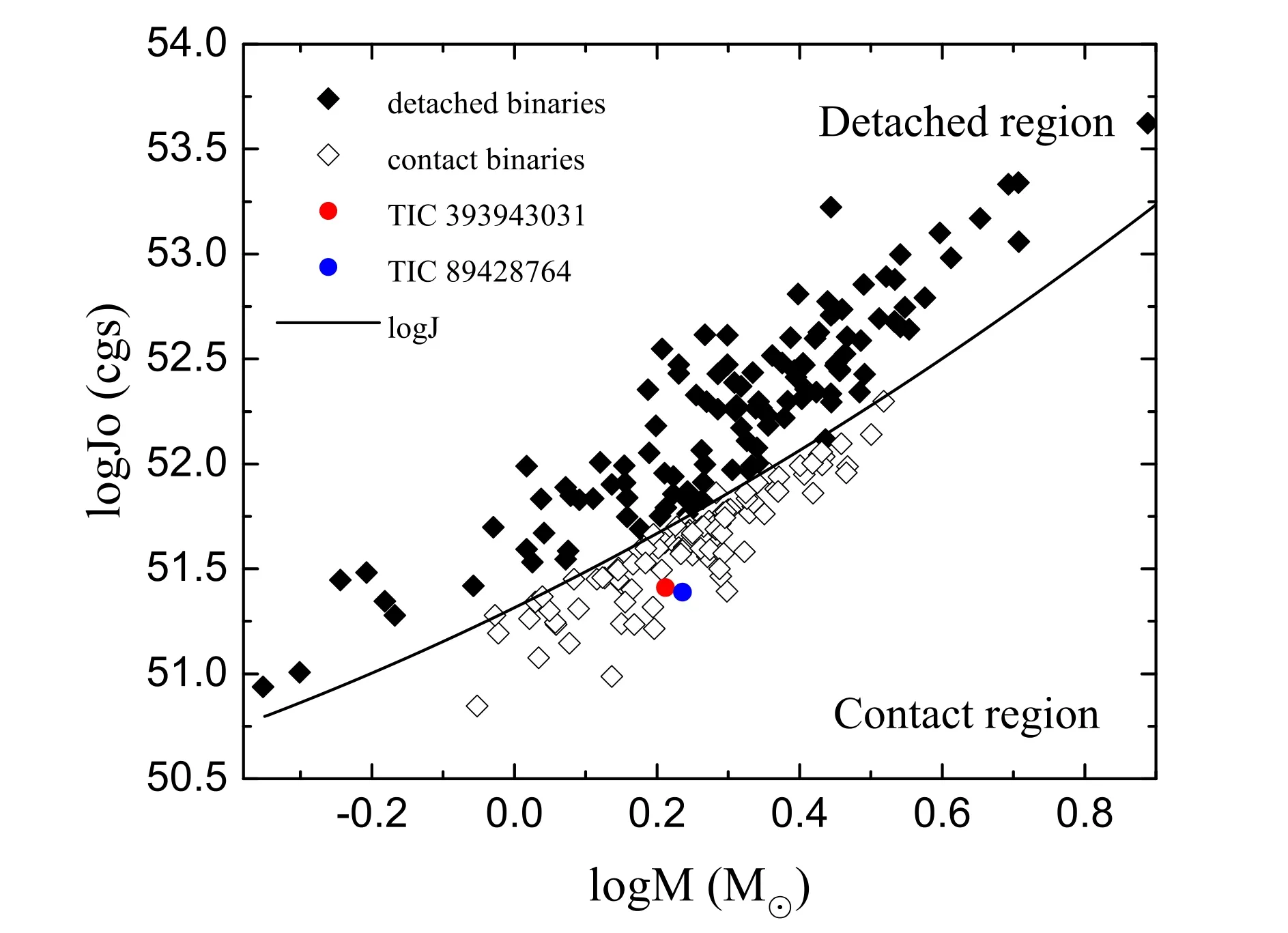
Figure 8.This figure displays the log M–log J0 diagram of TIC 393943031 and TIC 89428764.

5.Discussion

The photometric solutions of two eclipsing binaries TIC 393943031 and TIC 89428764 are presented for the first time.TIC 393943031 is a low-mass-ratio deep contact binary with a mass ratio of q=0.163±0.001,a fillout factor of f=50.8%,while TIC 89428764 is a low-mass-ratio medium contact binary with a mass ratio of q=0.147±0.001,a fillout factor of f=32.7%.Both the stars are A-subtype contact binaries.Through the analysis of minima,both of them display increasing periods,and the increasing rates are 4.21×10-7day yr-1and 6.36×10-7day yr-1,respectively.These are the same order of magnitude as the results obtained by Lohr et al.(2015).The reason for the long-term increasing in periods may be that the secondary star transfers mass to the primary star for the two binaries.The spectral type of TIC 393943031 is F5,while TIC 89428764 is F1.If the primary stars are main sequence stars,we can estimate their masses of primary and secondary.According to Cox(2000),the primary mass of TIC 393943031 is M1=1.40M⊙,while that of TIC 89428764 is M1=1.50M⊙.Then according to the mass ratio,their secondary masses can be calculated as M2=M1×0.163=0.23M⊙for TIC 393943031,and M2=M1×0.147=0.22M⊙for TIC 89428764.The mass transfer rates of TIC 393943031 and TIC 89428764 can be calculated as dM2/dt=7.12×10-8M⊙yr-1and dM2/dt=1.31×10-7M⊙yr-1using following Equation (8)

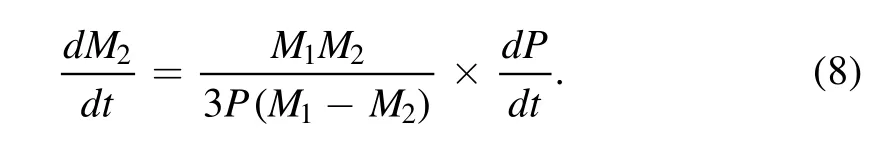
The distances between primary and secondary of the two targets can be deduced as a=2.91R⊙for TIC 393943031 and a=2.63R⊙for TIC 89428764 based on M1+M2=0.0134a3/P2.The radii of the primary and secondary stars of the two stars can be obtained according toa=0.63R⊙for TIC 89428764.Then,according to Stefan-Boltzmann’s law,the luminosities of primaries are respectively calculated as 4.12L⊙and 4.87L⊙.Those of their secondaries are determined as 0.78L⊙and 0.76L⊙.

In order to directly discuss the evolution state of the primary and the secondary stars,the mass–luminosity diagram of the two stars is displayed in Figure 7.In the figure,“ZAMS” and“TAMS” represent the zero-age main sequence and terminalage main sequence,respectively (Hurley et al.2002).Both primary stars of the two binaries are located between“ZAMS”and“TAMS”and the position of two secondary stars are above the “TAMS” line.From Figure 7,the primary stars are at the main sequence stage.The secondary stars may have evolved out of the main sequence,or the luminosity-excess of the secondaries can be the result of energy transfer from the primary to the secondary.

The orbital angular momentum is significant for the evolution of contact binaries,so we made an estimation for the orbital angular momenta of the two targets.The orbital angular momenta of the two stars have been determined asfor TIC 393943031 and logJ0=51.39for TIC 89428764 based on Eker et al.(2006)'s formula as follows,

The border line of contact and detached phase combined with the stars from Eker et al.(2006) are displayed in logM–logJ0diagram as Figure 8.From the figure,both stars are located in contact region.

In summary,TIC 393943031 and TIC 89428764 are both extremely low-mass-ratio A-subtype contact binaries.Using the O-C method to analyze their period variation,we found that both stars display long term increasing periods.The possible reason is that the secondary component transfers mass to the primary component.Furthermore,we estimated their absolute parameters and calculated the mass transfer rates.As the periods increasing,mass transfer will be carried on from the secondary stars to the primary stars,and the mass ratios will be lower and more extreme.Finally,they may merge into single stars (Qian et al.2005a).

Acknowledgments

We are grateful to the referee for the valuable suggestions and comments.This work was funded by the National Natural Science Foundation of China (grant Nos.U1931106 and U1931103),Shandong Provincial Natural Science Foundation of China (grant No.ZR2019YQ03) and Project of Shandong QingChuang science and technology plan (grant No.2019KJJ006).Great thanks to Dr.Wang,Z.H.for sending us the van Hamme (1993)’s table that has been added the TESS-band.This work includes data collected by the TESS mission.Funding for the TESS mission is provided by NASA Science Mission directorate.We acknowledge the TESS team for its support of this work.Thanks to Dr.Andraw Norton and Dr.Marcus Lohr for sending us the SuperWASP data.