基于孪生通道自相参的LPI 通信信号侦察方法
王 伟 ,王钦钊 ,郭傲兵
(1.陆军装甲兵学院兵器与控制系,北京 100072;2.北京特种车辆研究所,北京 100072)
0 引言
为适应日益复杂的电磁环境,无人平台测控链路信号要求具有较好的低截获性和抗干扰性能。低截获概率(LPI)通信信号以特殊的调制方式在非常宽的带宽上对信号频谱进行扩展,故LPI 信号也称扩谱信号或扩频信号,具有选择性寻址、传输隐蔽、抗干扰能力强的特征,采用常规方法的接收机很难探测。通常LPI 信号有三类:跳频信号、Chirp 信号和直接序列扩频(DSSS)信号。为提高传输安全性和抗干扰能力,一个LPI 信号可以组合使用多种扩频技术(也称为LPI 混合技术)。
无人系统的遥控遥测链路常使用LPI 信号,且调制方式和编码不易提前获取,因此通过辐射源侦测方式对其进行探测,需要采用可适用于信号参数未知的LPI 信号侦测方法。
李国华分析了LPI 扩谱信号的侦收问题,并提出了在电子侦察接收机上的改进思路;何如龙等针对跳频通信信号的侦察和分选方案进行了探讨;胡来招给出了侦收弱信号时的极限接收灵敏度,并指出了如何减少灵敏度损失;李斌等提出利用大数据、智能化等技术对电磁侦察数据进行挖掘,以得到更多高价值情报数据信息并提出了大数据挖掘的内容及主要处理技术;Lu Tingting 对正交频分复用(OFDM)系统中带有虚拟载波的空间交替广义期望最大化(SAGE)算法进行了研究,为解决虚拟载波的信道频率响应问题,通过迭代技术来最小化CFR 的误差以改善信道估计;Gouda 提出使用传统的三阶自相关累积量对直序扩频信号进行盲检测,但对频偏敏感;Shi针对直扩信号检测提出了基于四阶累积量的新算法,但性能不佳;Jin Yan 提出使用传统循环平稳谱进行检测,但复杂度较高;Fei 应用分形理论进行了直扩信号的检测;Uysal 提出了利用多天线的相位变化特征进行检测的算法;刘万贤则使用了基于波动自相关的检测算法对突发直扩信号进行检测。上述研究虽然均不同程度地实现了对直扩信号的侦收,但均存在性能欠佳、需要先验知识或参数估计、处理增益不高等问题;欧阳鑫信利用多跳信号互模糊函数进行相参积累,提升了时频差参数的估计性能,但在信噪比低于-1 dB 时与非相参方法区别不大。
本文提出了一种基于孪生通道自相参的LPI 通信信号接收方法,实现了较高的接收灵敏度。
1 扩谱调制信号的低截获特性
扩谱通信的产生主要依据香农定理和抗干扰理论。
根据香农定理,连续信道容量公式为:
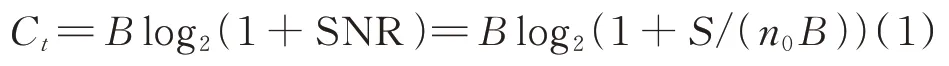
式中,为信道带宽,为噪声单边功率谱密度,=表示噪声平均功率,为信号平均功率。可以看出,在信道容量C一定的条件下,信道带宽与信噪比SNR 成此消彼长的关系,想要提高抗截获能力即降低SNR,可以通过增加来实现。
根据通信抗干扰理论,信息传输差错概率是关于SNR(B/B)的函数,B、B分别表示信号带宽和信息带宽。根据通信系统的抗干扰能力要求,通常限定其最大信息传输差错概率,以保证信息传输质量。由此处亦可看出扩谱调制与信噪比的关系。且在B一定时,SNR 直接与B有关。用如下公式表征扩谱系统的抗干扰能力,以代表其处理增益,它与B/B大致相当。
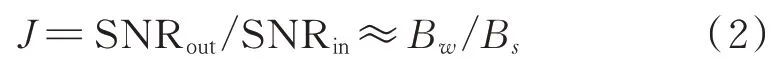
在信号理论中,电子侦察接收机灵敏度为:=KTB FM。其中,是玻尔兹曼常数,是接收机工作温度,B为接收机噪声带宽,KTB是电子侦察接收机通道内的噪声功率,为接收机信号通道的噪声系数,为信号检测所需的最小信噪比。减小接收机带宽B,可降低接收机通道内噪声功率,提高接收机的微弱信号检测能力,即提高其灵敏度。在常规通信侦察接收机中,B可小至 5 kHz,比 1 MHz 的接收机,其灵敏度要高10 lg(1 MHz/5 kHz)=23 dB。
对功率为P的信号,扩谱前后带宽分别为B和B。在频域观察信号,其功率将从B扩散到B,频谱密度下降到原来的B/B,这描述了扩谱信号的低截获特性。
从图1 可以看出,信号扩谱前后其频谱密度发生较大变化。电子侦察接收机带宽从B减小到B的过程中,接收机噪声带宽减小,接收机通道内噪声线性减小,进入接收机的功率不变,电子侦察接收机对该信号的灵敏度提高。
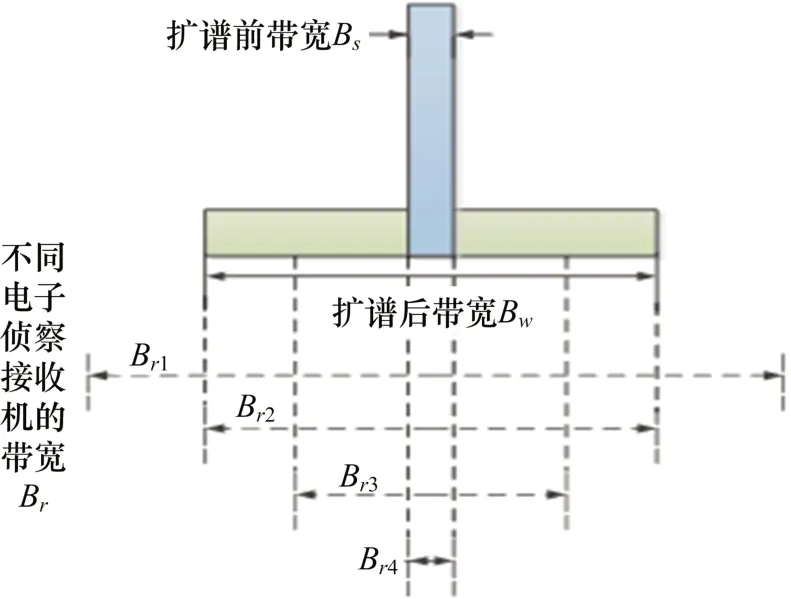
图1 不同电子侦察接收机带宽对扩谱前后信号带宽的比较
在接收机带宽由B减小到B的过程中,侦察接收机内噪声持续减小,进入接收机的未扩谱信号功率不变,接收机对未扩谱信号的灵敏度持续提高。而对扩谱信号,随着接收机带宽减小,进入到侦察接收机的信号功率相应减小,带宽为B、B、B的接收机对扩谱信号的灵敏度一样,侦察接收机的灵敏度没有提升。
因此,对于扩谱信号,侦察接收机对扩谱信号的最高灵敏度被限制在=KTB FM。
信号扩谱后,其带宽B越宽,信号被电子侦察接收机截获的灵敏度越低,这体现了扩谱信号的低截获特性。
以某国外小型无人平台的测控链路为例,其参数如下:通信距离:10 km;发射功率:0.1~0.5 W;图像数据率:1.1 Mbps;指令数据率:6.4 kbps;信号带宽:图像数据链信号20 MHz,指令数据链信号1 MHz。
在示例链路信号中,图像信号扩谱后带宽为20 MHz,扩谱前带宽为1.1 MHz(在BPSK中等于数据率),其低截获特性提升了 10 lg(20 MHz/1.1 MHz)=12.6 dB;指 令链路的低截获特性被提升了10lg(1 MHz/6.4 kHz)=21.9 dB。
从上面分析可见,图像链路和指令链路信号采用扩谱调制后,提高了链路信号的低截获特性。
2 侦察扩谱信号存在的问题
对小型无人平台测控链路进行侦察,面临2 个难题:
1)信号的低截获特性,降低了电子侦察的作用距离;
2)信号发射功率小,使得所需的接收机处理增益和灵敏度更高。
通常情况下,相参处理或匹配滤波处理,能够通过对信号的能量积累提高侦察灵敏度,但需要掌握信号的调制参数,获取信号处理增益。由于多数情况下被侦察的链路信号的扩谱调制参数未知,不能通过匹配滤波方式对其进行相参积累处理以提升接收机灵敏度。通常的做法是:
1)以非相参积累方法进行处理,提高接收机灵敏度;
2)采用体积更大、增益更高的接收天线以提高系统灵敏度。
以上做法带来的问题是:
1)采用非相参积累方法,如果对信号进行次非相参积累,信噪比提升约为,想要得到与相参处理相当的灵敏度,需要的时间开销将更大(如,要提高10 dB 的灵敏度,对链路信号的积累次数=100 次,时间开销增加100 倍);
2)采用更大的接收天线,如果系统灵敏度要提高10 dB,则根据天线理论,天线增益=4π/,天线有效接收面积将增加10 倍。
因此,受限于物理尺寸的约束,通常采用提高接收机灵敏度的方法来提高对链路信号的侦察能力。
3 基于孪生通道自相参的高灵敏度接收方法
3.1 非相参积累处理
为了充分说明孪生通道自相参的效果,将其与现有的时频域非相参积累增益进行对比。
2 个通道中信号的通用模型为:
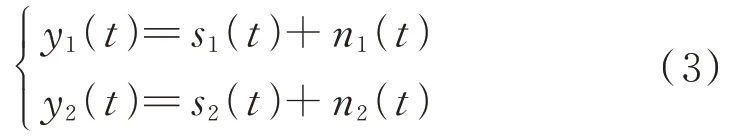
式中,()为待处理的信号,()为参考信号,()、()为互不相关的独立噪声信号。
2 个信号()和()的共轭乘法运算用⊗代表,则有:
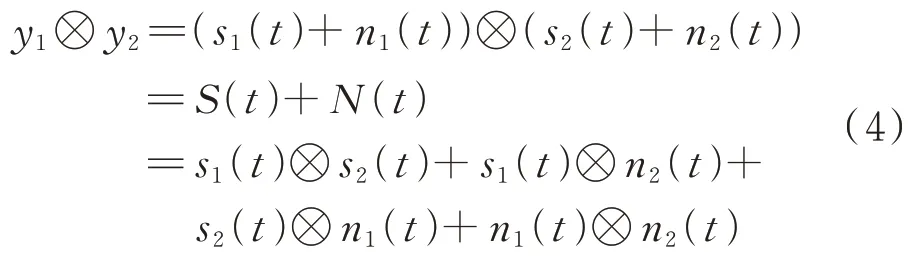
式中,()为有效信号,()为新噪声。
共轭乘法后,信号()的处理增益为:
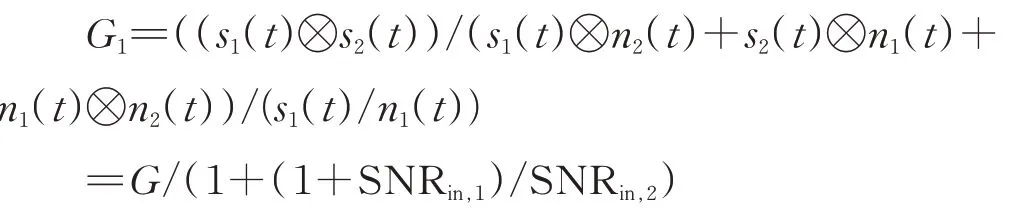
式中,=()⊗()表示共轭乘法的处理增益,SNR表示接收通道1 的输入信噪比,SNR表示接收通道2(其中的信号取为参考信号)的输入信噪比。
对于通信和雷达而言,信号处理是协作的,参考信号对应的信噪比SNR=+∞,即理想的孪生通道自相参处理增益等于。对于未知参数的链路信号,信号处理是非协作的,参考信号对应的信噪比SNR是一个有限值,这使得共轭乘法后处理增益损失为1+(1+SNR)/SNR。
3.2 相参积累处理及孪生通道自相参处理
基于孪生通道自相参处理的高灵敏度接收方法(以下简称“自相参处理”)原理如图2 所示。
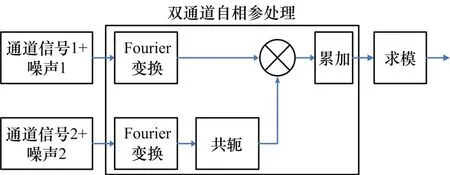
图2 基于孪生通道自相参处理的高灵敏度接收原理图
首先,需要满足以下2 点:
1)参考通道的信号()与接收通道的信号()的关系满足()=(-),其中为延迟时间,为幅度,这可以通过对信号的预先采样来实现;
2)参考通道信噪比SNR不小于接收通道信噪比SNR,这可以通过设计2 个完全相同的接收机来保证,采用相同的硬件设计和器件,并对通道噪声水平进行标定和校正,以保证2 个通道的一致性。
然后,将2 个通道中信号()的Fourier 变换与()的Fourier 变换的共轭相乘,并进行累加。
信号()的Fourier 变换为:
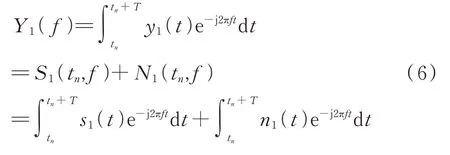
信号()的Fourier 变换为:
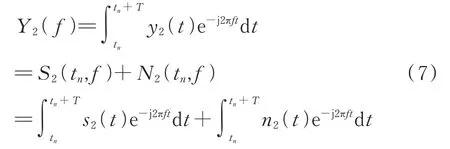
于是,时频域相参积累表达式为:
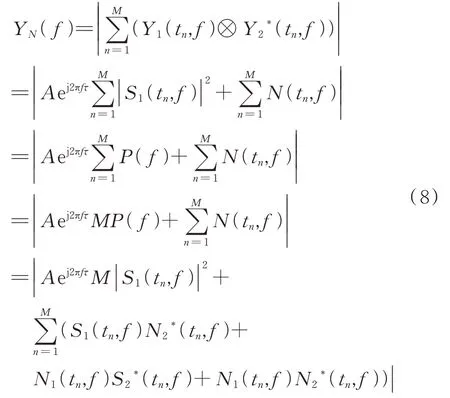
式中,*表示共轭运算;()表示信号()每次Fourier 变换后在频域上的功率形式;()表示信号()在频域上的能量表现形式,为次的能量叠加结果。
从式(8)可以看出,信号处理后包含 2 项:第 1 项为信号能量的频域表现形式,第2 项为新的噪声。经过次积累后,频域上的功率()变为能量·(),信号处理增益为。
自相参处理积累包含共轭乘法和相参积累2 个过程,因此相对于理想的相参积累增益,总的处理增益损失为:
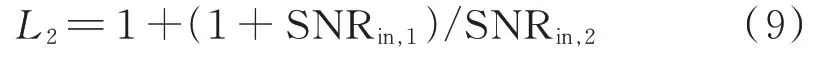
式(9)表明,相同条件下,SNR越大,则处理增益损失越小。显然,自相参处理积累的信号处理增益损失与积累次数无关,只与积累前的信噪比有关。相同条件下,SNR=SNR时,SNR越大则处理增益损失越小,反之越大,如图3 所示。
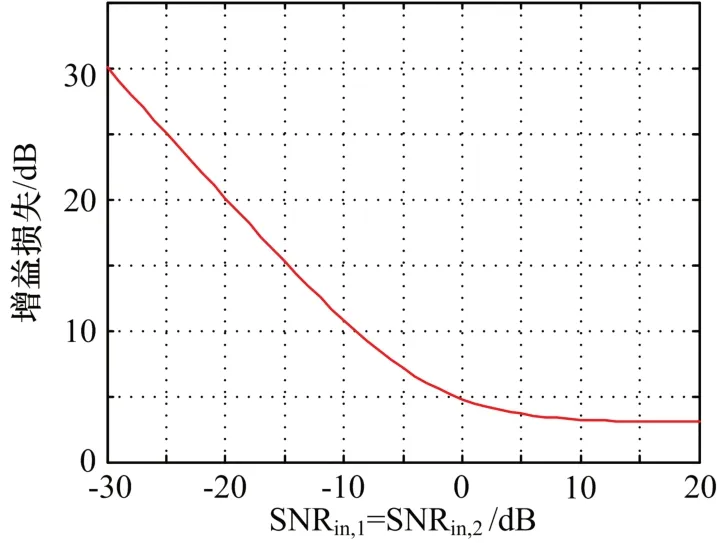
图3 自相参处理的积累损失与输入信噪比关系
从理论上分析,非相参处理、常规相参处理、自相参处理等辐射源侦察信号处理方法的特点及对比如表1 所示,表中为对接收信号的积累次数。

表1 辐射源侦察的信号处理方法对比表
从表1 可以看出,自相参处理具有以下特点:
1)与非自相参处理方法相比,在相同的信号积累次数和相同的信号处理时间下,自相参处理信号处理增益更高,提高了接收灵敏度;
2)与常规相参处理方法相比,自相参处理的参考信号为时刻前接收到的自身信号,因此无需事先知道信号调制参数,尤其是对扩谱调制信号,作用对象范围更广;
3)信号处理增益损失与积累次数无关,只与积累前的信噪比有关,弥补了现有非相参积累方法的信号处理增益损失随积累次数增加而增加的不足;
4)当积累次数足够大时,自相参积累比非相参积累能适应更低的输入信噪比,对电磁环境要求更低,应用场景更广泛。
4 仿真实验
通过仿真实验对比以下几种典型的高灵敏度接收处理体制的特点。
假设信号脉冲宽度为40 μs,系统采样率为500 MSPS,数据点数为20 000。4 种处理体制对应的参数如表2 所示。

表2 典型信号处理体制及参数设置
仿真实验一:单载频脉冲信号,样本点20 000,中频50 MHz,输入信噪比SNR=-17 dB(因第三种、第四种方法需要进行2 路自相参处理,会有预期额外增益,故将其每路的信噪比设置为-20 dB),试验结果如图4 所示。
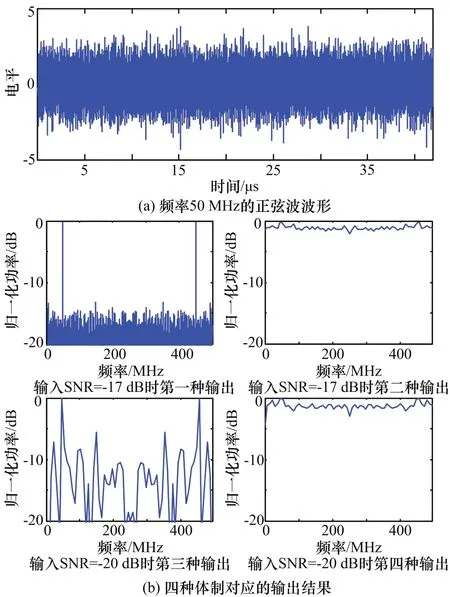
图4 几种体制对应的正弦波信号信噪比改善情况
从图4(b)四种处理方法的输出信号可以看出,对常规连续波信号,第一种处理方法(大点数FFT)输出信噪比最好,第三种处理方法输出信号可检测,第二、四种方法不能检测信号。
仿真实验二:线性调频信号,样本点20 000,初始频率50 MHz,调制带宽10 MHz,输入信噪比同仿真实验一,试验结果如图5 所示。
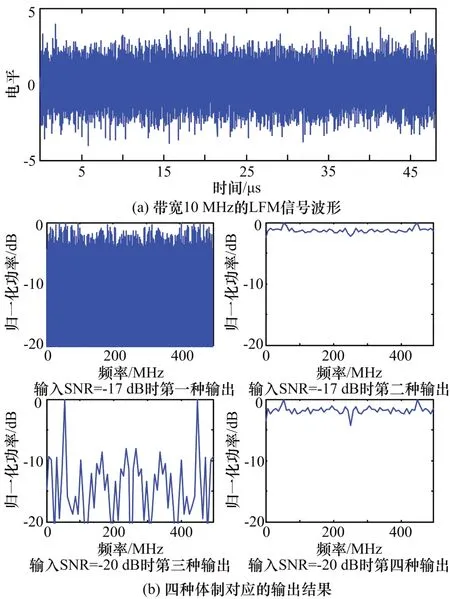
图5 几种体制对应的LFM 信号信噪比改善情况
从图5(b)四种处理方法的输出信号可以看出,对调频信号,仅采用“自相参处理+相参积累”的第三种处理方法输出信号具有可检测性,其它方法不能检测信号。
通过对比仿真实验一和仿真实验二的结果可以得出结论:
1)“大点数FFT”体制,难以适应低信噪比下的宽带信号检测与参数测量;
2)“小点数FFT+非相参积累”体制,对宽带信号低信噪比信号检测的适应性有所提高;
3)“自相参处理+相参积累”体制,在低信噪比条件下信号检测的适应性高于“小点数FFT+非相参积累”体制;
4)“自相参处理+非相参积累”体制,在低信噪比条件下信号检测的适应性低于“自相参处理+相参积累”体制。
可以看出,“小点数FFT+非相参积累”和“自相参+相参积累”比其余2 种方式获取的处理增益更高,“自相参处理+相参积累”的处理方法具有如下特点:事先无需信号调制参数、更高的处理增益、较低的增益损失、较高的接收灵敏度、很好的宽带信号适应性。
以上仿真实验表明,基于孪生通道自相参的处理方法,在一定条件下具有更高的接收灵敏度,可以用于侦收具有低截获特性的扩谱链路信号,可有效提高对地面无人平台及测控站的侦察距离和探测概率。
5 结束语
在日益复杂的电磁环境下利用传统的信号侦察方法对LPI 通信信号进行侦察,面临着信号参数未知、接收灵敏度低、对输入信噪比要求较高等问题。本文提出的基于孪生通道自相参的LPI 通信信号接收方法,能够提高复杂电磁环境下对LPI 通信信号的侦察接收能力,实现对无人平台测控链路的高效侦察探测,进而对无人平台或其操控站进行侦察定位,并对其实施干扰反制,对开展反制无人平台研究具有较重要的参考价值。

