基于SVD与机器学习的华南降水预报订正方法

谢 舜 孙效功 张苏平 熊朝晖 魏晓敏 崔丛欣

1)(中国海洋大学海洋与大气学院， 青岛 266100)2)(中国气象科学研究院， 北京 100081)3)(武汉大学测绘学院， 武汉 430079)4)(陕西省气象局机关服务中心， 西安 710014)

引 言

华南前汛期(4—6月)是我国进入夏季雨季的第一阶段，也是暴雨频发时期，该阶段总累积降水量超过1000 mm，约占华南地区全年降水量的一半[1]。过程频发和降水量大等特征导致该时期华南地区极易发生洪暴、山体滑坡等气象灾害，造成人员财产重大损失。因此，提高华南降水预报准确率，是当前预报业务中的重要工作之一。降水是数值预报难度较大的气象要素之一，具有复杂的非线性过程、不服从正态分布、不连续等特点，相较于温度、风等气象要素预报难度更大[2-3]。目前，降水预报主要参考数值预报产品，但大气运动的高度非线性、机理认识有限等原因，模式预报仍然存在误差[4]。许多研究表明:华南前汛期降水可分为锋面性降水和热带季风性降水。以南海季风爆发时间为转折点，南海季风爆发前，华南上空受西风带低压槽扰动影响，高纬度干冷空气与低纬度暖湿空气相遇，形成强度大、持续时间长、范围广的锋面性降水；南海季风爆发后，由于水汽源地发生改变，水汽输送通量增强，降水类型转变成强度更大、对流更剧烈、雨区范围变小的暖区中尺度强对流降水[5-7]。受降水成因的复杂性和机理认识不足等限制，数值模式降水预报能力的提高受到很大制约，导致降水预报技巧提升相对缓慢[8]。如何减少模式预报的系统误差影响，探讨更加有效的模式降水预报误差订正方法，提高模式预报产品的解释应用水平，一直是气象科研和业务关心的热点问题。近年模式预报误差订正技术不断发展与完善，模式后处理预报订正多基于传统的统计订正方法[9]。李莉等[10]采用分区订正方法发展的T213降水预报订正系统，可有效针对不同地区降水控制系统的差异，多个研究也发展了更具针对性的区域降水订正技术[11-12]。苏海晶等[13]根据文献[14-15]提出的历史数据动力-统计思路的基础，采用历史降水观测数据与动力模式降水预报资料进行奇异值分解(singular value decomposition,SVD)方法，对我国夏季降水进行误差预测订正，结果表明：SVD方法对降水预报有一定改进作用。SVD方法是研究两个空间场相关关系的诊断方法，王建新[16]、刘宗秀等[17]将其用于我国长江梅雨期降水场与500 hPa高度场的诊断分析，也被用于因子场与预报场的预报或订正[18-20]。随着机器学习方法的发展，机器学习也为降水订正研究工作开辟了新途径。机器学习方法是基于统计学原理，能自主学习样本各特征之间的关系，在降水预报以及订正工作中均得到广泛应用[21-22]。Krishnamurti等[23]首次提出超级集成方法后，许多研究也相继采用该方法对多模式进行降水集成订正[24-27]，该方法能有效融合模式的各种信息提高预报技巧。本文将SVD、机器学习和加权集成相结合，提出模式降水预报产品的订正方法。其中，SVD方法用于获取模式降水预报产品与观测场之间的耦合信息，机器学习方法用于构建耦合信息与降水观测值的超函数关系订正模型，加权集成用于多个订正模型的输出集成，以寻求更优的模式降水预报产品订正方法。

1 数据与方法

1.1 数 据

本文采用欧洲中期天气预报中心(European Centre for Medium-Range Weathre Forecasts, ECMWF，以下简称EC)确定性降水预报产品，该产品为20：00(北京时，下同)起报的24 h累积降水数据，空间分辨率为0.25°×0.25°。观测数据为中国地面基本气象要素日值数据集(V3.0)中华南区域20:00—次日20:00日降水数据。经过数据整理筛选后，得到445个气象观测站信息(图1)。将EC模式预报产品与站点观测数据进行时空匹配，空间匹配采用双线性插值方法，将EC模式预报产品插值到站点，插值过程中个别站点出现负值，且其数值接近于零，为避免负降水现象发生，此类站点的降水插值全取为0。本文研究的华南区域范围为18°～28°N，105°～120°E，时间范围为2007—2019年4月1日—6月30日。

图1 华南地面气象站分布Fig.1 Distribution of ground sites in South China

1.2 订正方法

首先将数据集分成训练集(2007—2017年)与测试集(2018—2019年)，训练集用于构建最优参数订正模型，测试集用于订正模型的检验与分析。SVD方法用于获取模式降水预报产品和观测场之间空间模态与时间系数，机器学习用于构建时间系数与降水观测值的函数关系，最后将加权集成方法用于融合多个订正模型，获得更优的降水预报订正值(图2)。

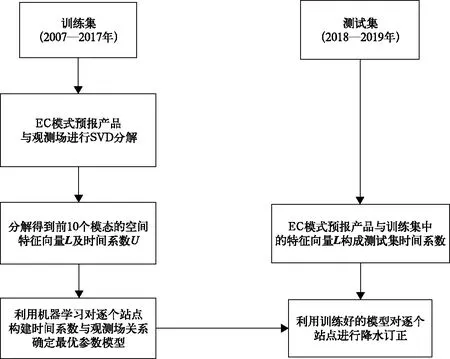
图2 订正流程Fig.2 Correction process

1.2.1 奇异值分解(SVD)

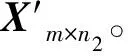
(1)

(2)

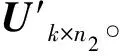
S=XYT=LART，

(3)

A=diag(σ1,σ2,…,σr)，r≤m，

(4)

(5)

(6)

表1 前10个模态累计方差贡献Table 1 Cumulative variance contribution of the top 10 modes

1.2.2 基于机器学习方法构建时间系数与降水观测值关系

机器学习是一种基于统计学的计算机建模方法，它可根据给定损失函数不断地迭代更新权重，进而建立输入量与输出量的最优超函数关系[31]。

本研究尝试采用十折交叉验证和网格搜索的方法构建最优参数模型。十折交叉检验是将样本随机分成相等的10份，采用其中9份用于模型训练，剩余1份用于检验，如此不重复进行，从而获得最优参数模型。网格搜索是将模型进行多参数排列组合，利用十折交叉检验方法，确定最优参数。本研究已尝试的机器学习方法包括线性回归、K近邻算法(K-nearest neighbor)[32]、随机森林(random forest)[33]、反向传播神经网络(back propagation neural network)[34]。结果发现，K近邻算法、随机森林与反向传播神经网络在构建时间系数与降水观测值关系上不如线性回归方法，订正后的华南降水平均均方根误差高于EC模式预报产品。这说明并非模型算法结构越复杂效果越好，此前已采用SVD方法对输入量进行降尺度处理，复杂模型此时更容易出现过拟合现象，因此需要针对不同数据集寻找合适的订正模型。基于上述原因，本研究采用多元线性回归(multiple linear regression，MLR)、套索回归(LASSO regression)、岭回归(Ridge regression)，3种机器学习方法及矩阵求解法，分别与SVD结合构建订正模型。将模型应用于测试集，可求得每个订正模型的降水订正值Xm,i(i=1,2,3,4)。

多元线性回归、套索回归、岭回归以及矩阵求解法的目标函数一般表达式如式(7)所示，其中U为经过SVD分解获得的前10个模态的时间系数。对求取最优回归系数，传统方法运用矩阵求解方法获得(式(8))[30]，而机器学习方法则以梯度下降法求解获得。套索回归、岭回归则是在多元线性回归的损失函数基础上加入正则化因子，通过不断迭代达到最优参数模型。研究表明：加入正则化处理能很好地解决因子间共线性问题，有利于防止过拟合，具有更强的鲁棒性，关于上述模型详细的算法见参考文献[35-36]。

k=1,2,…,10，

(7)

θ=(UTU)-1UTY。

(8)

其中，f(u)为订正模型目标函数值，θ为回归系数αi组成的列向量，U为时间系数ui组成的列向量，k为模态序号,ε为偏置系数，Y为降水观测序列矩阵。

1.2.3 加权集成方法

将SVD与多元线性回归、套索回归、岭回归、矩阵求解法相结合的多个订正模型所得到的降水订正值及EC模式预报产品进行加权集成，具体计算方法分别如式(9)～式(10)所示。为充分利用样本，这里采用十折交叉检验中验证集均方根误差的平均值作为定权依据。

(9)

(10)

2 订正结果

2.1 EC模式降水预报产品误差

由于地形、下垫面性质差异，华南不同区域EC模式降水预报产品的均方根误差分布存在差异(图3)，2018—2019年模式预报产品在华南的区域平均均方根误差为13.82 mm·d-1。总体上，误差相对较小的站点主要位于华南的西北部，误差相对较大的站点主要分布在珠江三角洲河口地区、各省交界地带、海南北部等地。珠江三角洲特殊的喇叭口地形，有利于大气中水汽辐合上升进而增加了降水的剧烈变化，导致预报误差较大。福建与广西交界的武夷山、湘赣粤桂4省交界的南岭，受复杂地形影响也难以达到较高的预报精度。此外，该时期由于南海扰动云团较为活跃，在东风波引导下，海南北部处于云团下游地带，加之海峡效应的作用，使得海南北部附近站点出现不稳定天气过程较多，以致该区域模式降水预报偏差相对较大。

2.2 机器学习降水预报误差订正

基于SVD与机器学习相结合的订正模型，对2018—2019年测试集进行降水订正试验。其中，SVD与多元线性回归相结合的订正模型定义为模型Ⅰ，SVD与套索回归相结合的订正模型定义为模型Ⅱ，SVD与岭回归相结合的订正模型定义为模型Ⅲ，SVD与矩阵求解法相结合的订正模型定义为模型Ⅳ。本文利用优化率定量评估模型订正效果，优化率定义为EC模式预报产品与订正后的均方根误差之差，与EC模式预报产品均方根误差之比(单位：%)。上述各订正模型订正后的华南区域降水预报均方根误差均小于EC模式预报产品，且误差最大优化率达4.2%(表2)。图4为不同模型(方法)与EC模式预报产品的均方根误差差值对比。其中，负值表示订正后的均方根误差小于EC模式预报产品，说明订正有效(以下称为正订正)；正值表示订正后的均方根误差大于EC模式预报产品，说明订正无效(以下称为负订正)。

试验结果表明：各订正模型对华南区域降水的订正效果总体上表现为正订正，尽管部分站点存在负订正现象，但大部分站点(超过69%)的均方根误差小于EC模式预报产品。

表2 不同模型(方法)订正效果Table 2 Correction effect in different models and method

图4 不同模型(方法)与EC模式预报产品均方根误差差值对比(a)模型Ⅰ,(b)模型Ⅱ,(c)模型Ⅲ，(d)模型Ⅳ,(e)加权集成方法Fig.4 Comparison of root mean square error difference of different models,method to EC product before and after correction(a)model Ⅰ,(b)model Ⅱ,(c)model Ⅲ,(d)model Ⅳ,(e)weighted ensemble

比较发现，不同模型订正幅度区间占比相近，存在细微差异(图5)。对于正订正，以正订正幅度越大越优，总体占比越高越优；对于负订正，以负订正幅度越小越优，总体占比越低越优。基于以上原则，从正订正看，SVD与机器学习相结合的订正模型(模型Ⅰ～模型Ⅲ)效果更优，虽然模型Ⅳ在正订正幅度最大区间占比最高，但该区间的站点基数小，整体订正优势不显著；从负订正看，SVD与矩阵求解法订正模型仅在订正幅度区间(3,5]优于其余模型。

总体而言，虽然模型Ⅳ最大幅度的正订正占比高于其他订正模型，但其负订正相对更为显著；而模型Ⅰ～模型Ⅲ订正效果相对保守，订正幅度虽小，但其整体区域正订正效果的占比更高，负订正的占比更小，订正效果更为理想。

2.3 多订正模型加权集成降水预报误差订正

由于不同订正模型各有优势，这里按照式(9) ～式(10)将EC模式预报产品与以上4种订正模型降水订正值进行加权集成。结果表明：应用加权集成方法得到华南降水均方根误差为13.01 mm·d-1,小于EC模式预报产品，也小于任一订正模型，优化率达到5.7%，为所有订正模型最高。加权集成后，正订正累计占比超过77%(图5)。可见，加权集成方法能进一步降低华南降水预报的均方根误差，扩大订正优势，订正效果更优。

图5 正负订正幅度站点数占比(a)模型Ⅰ,(b)模型Ⅱ,(c)模型Ⅲ,(d)模型Ⅳ,(e)加权集成方法Fig.5 Ratio of positive and negative sites to the correction amplitude(a)model Ⅰ,(b)model Ⅱ,(c)model Ⅲ,(d)model Ⅳ,(e)weighted ensemble

2.3.1 正、负订正个例站点对比

为探寻个别站点大幅度正、负订正的原因，这里选取加权集成的广东天等、广东徐闻、海南儋州、广东三水4个负订正代表站点及广东和平、贵州镇远、广西平南、广西武宣4个正订正代表站点(图6)，进行个例分析。图7为上述代表站点对应的EC模式预报产品、观测值以及集成订正值的序列。由图7可见，正订正的4个代表站存在模式产品空报强降水，经过订正可优化由此引起的均方根误差偏大的问题。而负订正的代表站点普遍存在1次日累积降水量大于200 mm的极端降水过程。2018年6月9日前后，三水、徐闻及儋州出现由台风艾云尼(1804)引起的强降水过程。由于华南前汛期降水以锋面性降水和热带季风性降水为主，台风系统引起的降水主要集中发生在华南后汛期，当用SVD选取空间特征时会以噪音的信息滤掉，所以对于台风降水的订正仍需单独探讨，以获得针对台风系统引起强降水的更优订正模型。

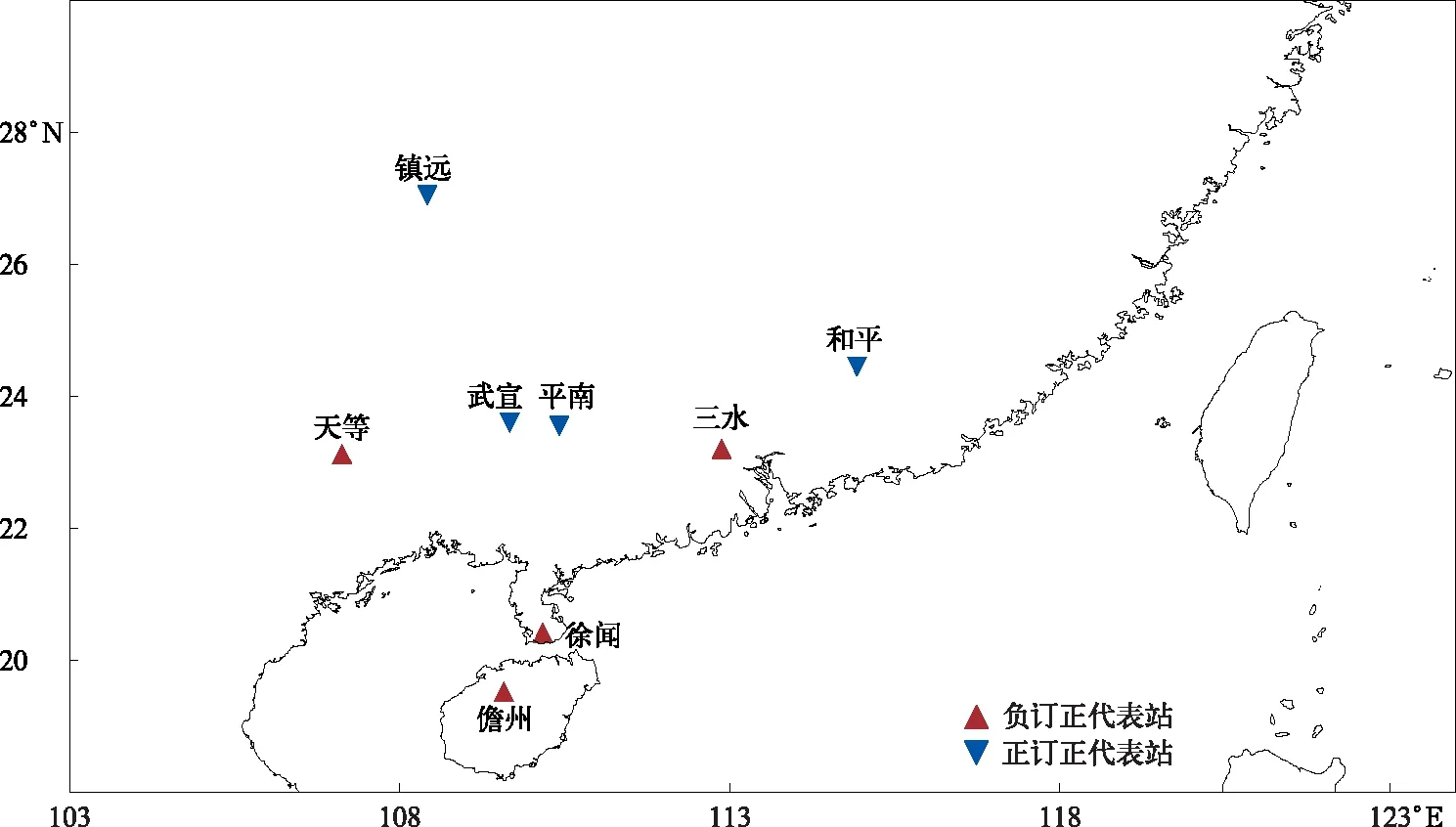
图6 个例代表站点位置分布Fig.6 Distribution of individual representative sites

图7 正、负订正单站对比(RMSE1为EC模式预报产品的均方根误差，RMSE2为加权集成订正后的均方根误差)Fig.7 Comparison of positive and negative correction sites(RMSE1 is root mean square error of the EC product，RMSE2 is root mean square error of weighted ensemble)

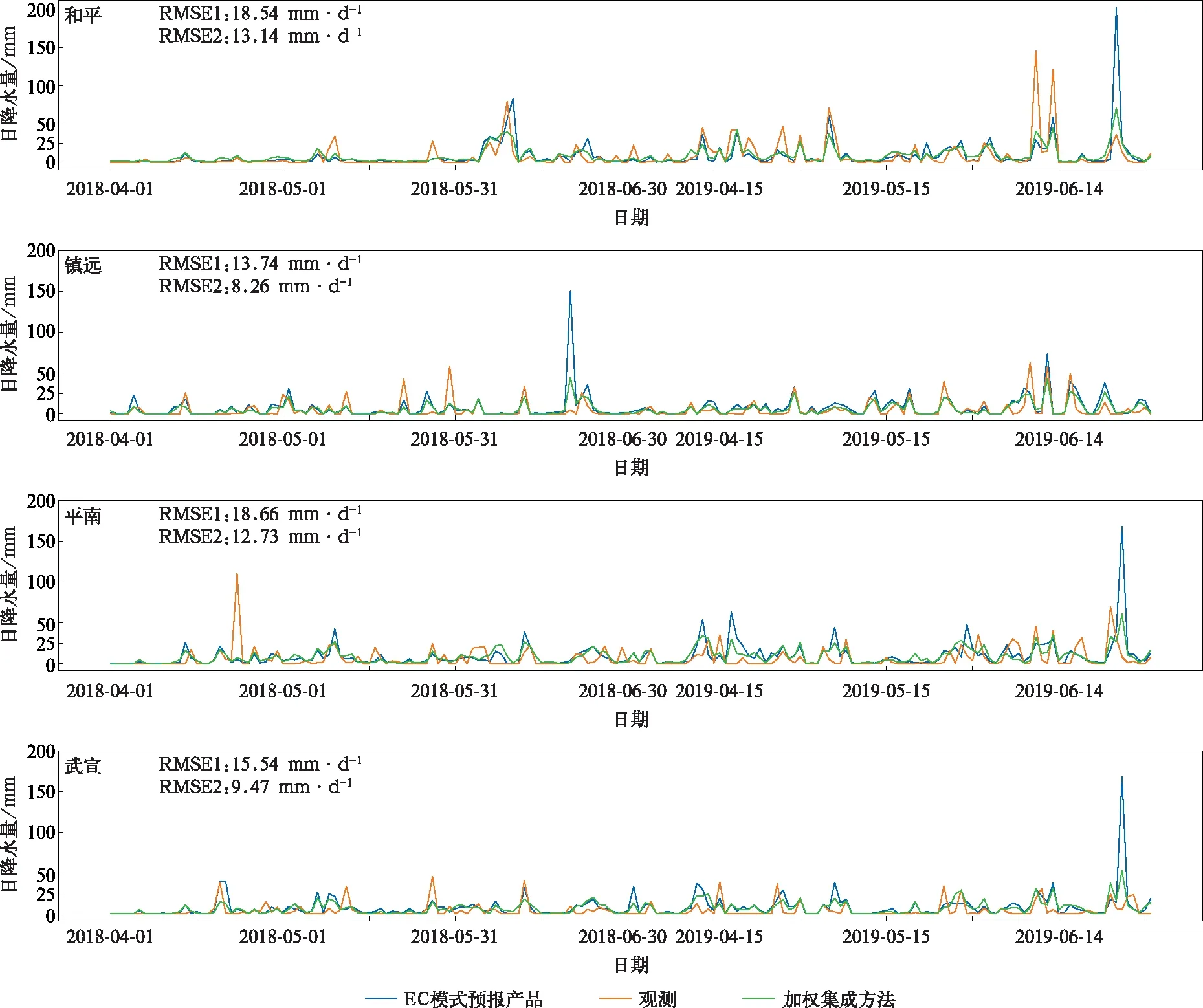
续图7

2.3.2 降水个例订正

图8展示加权集成订正前后的两次降水个例。2018年6月12日的降水个例是以华南中西部为降水中心的降水过程，图8中显示EC模式预报产品对降水预报存在雨区范围偏大、部分站点降水量高估的现象。经过加权集成订正后，虽然降水落区无明显优化，但在降水定量预报上改善明显，部分降水高估的站点订正后更接近降水观测值。对于2019年5月9日的降水个例，此次降水中心出现在华南东南部沿海和海南，图8中显示EC模式预报产品对该日降水落区预报范围、降水量预报偏小。通过加权集成订正后，两个降水中心得到更好体现，基本能完全覆盖所有出现降水的站点，虽然订正后落区范围较实际略偏大，但基本上能确保所有出现降水的站点不存在漏报。

图8 2018年6月12日和2019年5月9日两次降水个例订正Fig.8 Comparison of two precipitation cases on 12 Jun 2018 and 9 May 2019 before and after correction

续图8

3 结论与讨论

本文基于SVD与机器学习(多元线性回归、套索回归、岭回归)及矩阵求解法相结合构建订正模型，将多个订正模型进行加权集成，并对EC模式预报产品在华南前汛期降水预报进行订正研究，得到以下结论：

1) 文中提出的订正模型(模型Ⅰ～模型Ⅳ)对华南前汛期模式降水预报产品订正均具有一定订正效果，订正后的整体均方根误差均优于EC模式预报产品。

2) 相比于SVD与矩阵求解法相结合的订正模型，SVD与机器学习方法相结合的订正模型(模型Ⅰ～模型Ⅲ)效果更优，累计正订正的占比更高。机器学习方法能自主地对样本进行经验学习构建超函数关系，同时对损失函数添加正则化项能更好地处理因子共线性问题，鲁棒性更高。

3) 鉴于不同订正模型的差异，通过对不同订正模型赋予不同权重，进行多个订正模型的加权集成。加权集成方法在华南区域整体均方根误差小于EC模式预报产品，也小于任一订正模型。表明加权集成方法能更好地融合多个订正模型优势，将优势进一步扩大。

4) 从单站个例分析结果看，加权集成方法能减小EC模式预报产品对强降水空报引起的预报误差，使订正后的降水量与降水观测值更接近。

值得注意的是，华南前汛期降水主要以锋面性及热带季风性降水为主，使用SVD提取特征时，会将台风等其他在华南前汛期占比贡献较小的模态以噪音形式滤掉。从单站个例分析发现，该方法对极端强降水订正效果不佳，极端降水的控制系统复杂多样，需寻求其他的订正方法单独加以订正。