基于OpenFOAM的桩基透空堤结构尺度其透射系数的影响
夏曦,张可新,桂劲松
(大连海洋大学 海洋与土木工程学院,辽宁 大连 116023)
透空式防波堤不同于传统的实体式防波堤,堤身透空,便于海水交换,有利于改善港内水质,是保护生态环境的防波堤主要形式之一,其透水率高、挡浪效果好,对海底地质要求不高,可建于软弱地质区域,且结构简单、施工方便。目前,随着人们对海洋环保意识的提高及国家海域使用政策的调整,在主要海区已不支持新建实体式围填海工程,因此,今后大量采用透空式海岸工程结构已成为一个必然选择。
关于桩基透空堤,国内外学者已做了一些研究工作,并取得了一定成果。1947年,Ursell[1]最早提出该结构,并与Wiegel[2]从理论上研究了挡板透空式防波堤的透射和反射性能。Newman[3]在假定无限水深,两个挡板间的距离很小的情况下,建立了波浪透射系数的渐进理论。Chakrabarti[4]对桩基透空堤结构进行了物理模型试验,当水粒子通过挡浪板时,能量耗散发生,两组板内的波损失了较大的能量,并揭示了其透射系数的机理。很多学者研究了双垂直板防波堤在不同工况下相对堤宽、相对水深对消浪性能的影响[5-6]。Brossard等[7]研究了在不规则波作用下,透空堤结构的透射效应与波数之间的关系。对梯形防波堤[8]、多层水平挡板透空式防波堤[9]透射系数也进行了深入研究。胡亚娴[10]利用OpenFOAM软件建立二维数值水槽,研究了挡浪板相对入水深度对透空堤消浪特性的影响。才瀚涛等[11]应用特征函数展开法研究了孤立波作用下透空堤的透射解析解,孤立波作用下透空堤消浪性能的研究也是目前学者重点研究的内容[12]。
尽管针对双挡板透空堤的研究已较多,但未发现类似《防波堤与护岸设计规范》(JTS-2018)[13]的可供设计参考的双侧挡浪板结构定量关系,所以对双侧挡浪板桩基透空堤的堤顶宽度、挡浪板入水深度的合理取值范围进行深入探讨具有重要意义。本研究中,主要针对相对堤宽(B/L,B为堤宽L为波长)及挡板相对入水深度(Δ/H,Δ为挡浪板入水深度,H为入射波高)对双挡板透空堤透射系数的影响开展了系统的研究,并确定相对堤宽和挡板相对入水深度的合理取值范围,以期为实际工程设计提供科学参考。
1 数值模型控制方程及边界条件
控制方程为连续性方程、引入相体积分数α的动量方程及流体体积法(VOF)方程,其计算公式为
∇·u=0,
(1)
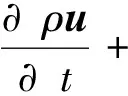
ρg∇x-∇pρgh+S*,
(2)
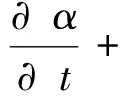
(3)
ρ=αρ1+(1-α)ρ2,
(4)
μ=αμ1+(1-α)μ2。
(5)
其中:u为平均速度矢量;t为时间;Ck∇α为表面张力项,C为表面张力系数,k为自由面的曲率;g为重力加速度;x为位置矢量;ur为相对速度,含有ur的项为人工压缩项,只在二相交界面处起作用;p为压力;S为阻尼项;h为波高;v为速率;ρ和μ分别为二相流的平均密度和平均动力黏度系数,ρ1为水的密度,ρ2为空气的密度,μ1为水的动力黏度系数,μ2为空气的动力黏度系数。
另外,除仿物理造波边界,本研究中只用到了固壁边界,故速度和压力采用不可滑移边界条件:
u|wall=0,
(6)
∂p/∂n|wall=0。
(7)
2 模型验证
2.1 物理模型试验设计
表1为某交通码头改扩建工程模型试验波浪要素,本研究中基于该工程对桩基透空堤进行了拓展研究。
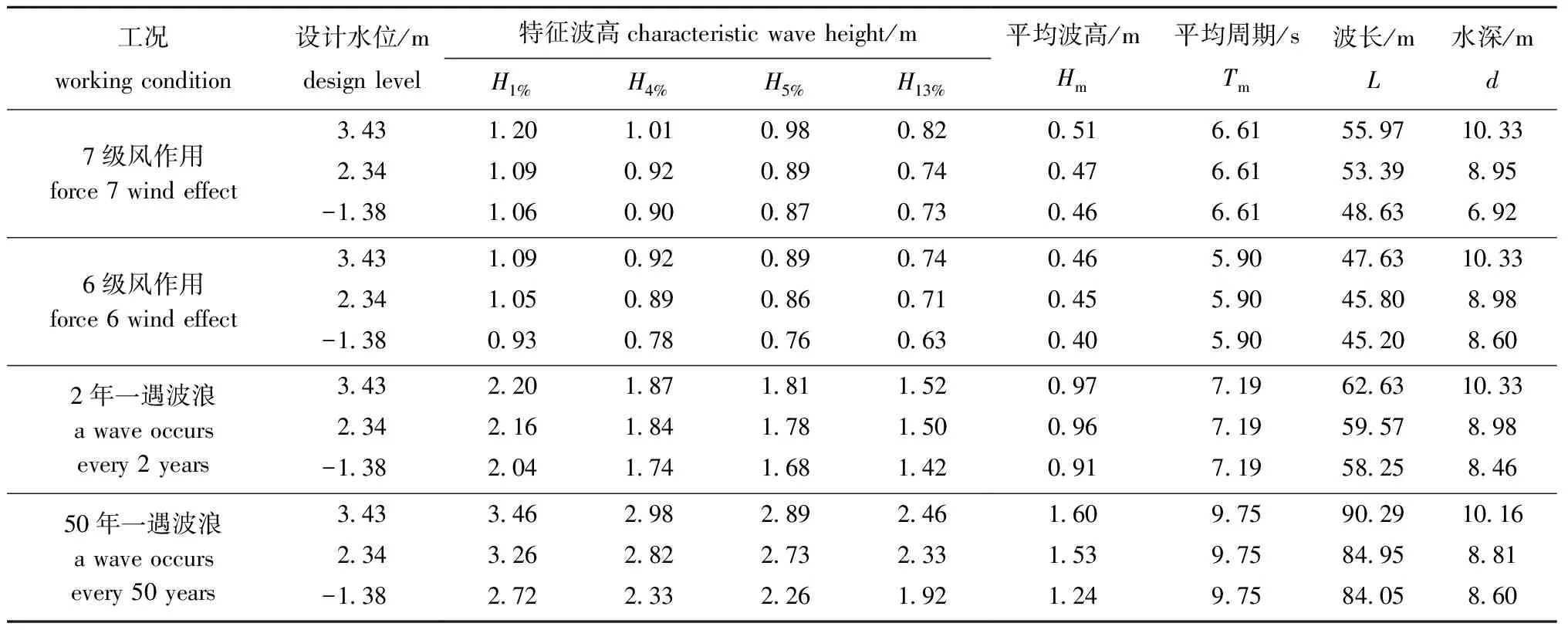
表1 某交通码头改扩建工程模型设计波浪要素
物理模型试验在大连海洋大学辽宁省海岸工程重点实验室进行,试验水槽条件采用恒定水深d=0.3 m,考虑表1及实际工程的需要,将实际工程中的水深条件暂定为7~12 m,故物理模型试验所选定的试验比例尺为1∶23~1∶34。参考《水运工程模拟试验技术规范》(JTS/T 231—2021)[14]对物理模型试验的要求,采用正态模型,按照Froude数相似定律设计,经过论证本试验的模型尺度取为1∶25,试验水深取0.3 m,相当于实际水深7.5 m。
物理模型试验采用规则波,根据表1原型波浪周期为5~9 s,考虑尽量包括长短周期,所以模型中波浪周期拟定为1.0、1.2、1.8 s。在水深d=0.3 m下的波长分别为1.37、1.77、2.89 m。根据表1设计波高并结合物模试验比例尺,物理模型中波高分别取为0.04、0.06、0.08、0.10、0.13 m。物理模型试验中使用的波浪要素见表2。

表2 试验工况
试验水槽布置如图1所示,水槽的左端是造波机,右端设有消波区;在结构的左端放置两个浪高仪(WG1、WG2)测量入射波高,防波堤后放置两个浪高仪(WG3、WG4)测量透射波高;结构物在水槽中后区域放置,距水槽前端造波区域约28 m。结构物主要由前挡浪板、后挡浪板组成,前、后挡板固定尺寸为0.700 m×0.300 m×0.025 m。试验中通过挡浪板下端有机玻璃条的拆装来控制挡浪板的入水深度,每条尺寸为0.700 m×0.025 m×0.025 m。波浪测量采用波高水位测量仪(DS30),波面数据采集使用多功能监测系统(DJ800),在试验前对浪高仪进行校准。

图1 物理模型试验布置图
2.2 数值模拟试验设计
数值模拟采用OpenFOAM水动力学软件,运用有限体积法进行空间离散。数值波浪水槽的尺寸为21.7 m×0.7 m×0.8 m,水槽的左端为造波区,右端为阻尼消波区,结构物距离造波端3L,阻尼消波区长度1.5L。由于采用动网格模拟物理模型试验中的推板造波,造波区距结构物不宜过远,故数值模拟水槽的长度小于物理模型试验水槽。在结构物前后各设置两个波面测点,测点距结构物位置与图1一致,利用VOF法捕捉波面。采用BlockMesh程序生成背景网格,水槽上部为空气,下部为水,在水气交界面网格采用SnappyHexmesh程序,对网格进行局部加密处理。
在确定牛羊患口蹄疫症后,应该在对其进行隔离的同时进行积极的治疗,最大程度提升牛羊恢复健康的可能。在进行治疗的过程中,要针对牛羊实际发病情况来进行处理,例如牛羊出现口腔溃疡的时候,可以通过在溃疡面上涂抹冰硼散或者碘甘油来进行处理。在如果在治疗的过程中出现牛羊病死的情况,应及时对尸体进行焚烧或者深埋,并进行消毒处理,降低其他牛羊感染的可能。
本研究中对数值模型的网格收敛性进行了验证,数值波浪水槽水深(d)恒定为0.3 m,波浪参数中,波高H=0.08 m,周期T=1.8 s。选择4种尺度的网格计算了波面变化。网格参数见表3。
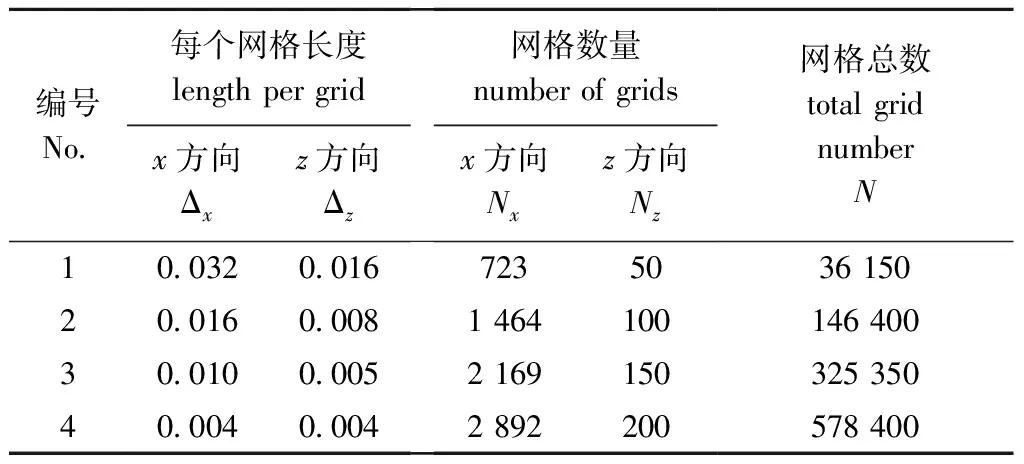
表3 网格参数
2.3 验证结果
图2为空水槽时结构物测点位置处采用4种网格尺度所计算的波面结果,当网格尺度(长×宽×高)分别为0.010 m×0.005 m×0.005 m和0.008 m×0.004 m×0.004 m时,波面已平稳,表明网格已收敛,考虑到计算效率等问题,本研究中选取0.010 m×0.005 m×0.005 m作为网格尺度。
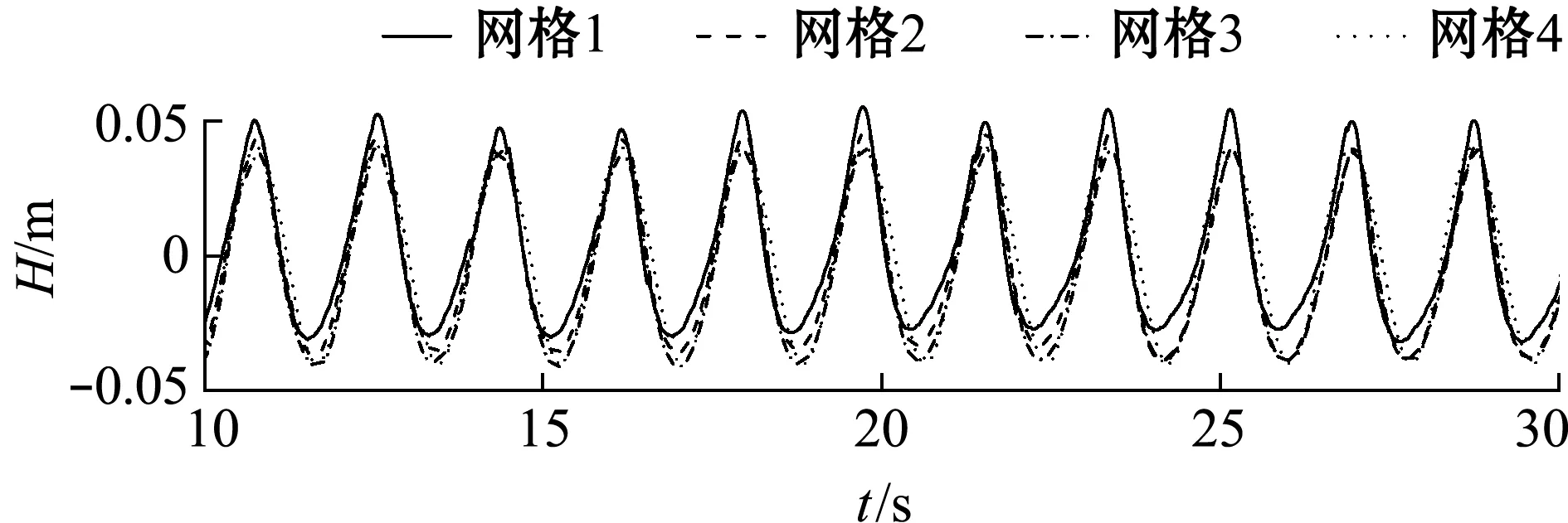
图2 不同网格尺度的波面历时曲线比较
图3为T=1.8 s、d=0.3 m、H=0.06 m时,物理模型试验波面与数值模拟试验波面入射波、反射波和透射波的对比结果,反射波分别为WG1和WG2测得的合成波分离的波面,透射波为WG3测得的波面,由于WG3测得的透射波和WG4测得的透射波基本一致,故在本研究中只选择WG3波面进行对比。从图3可见,物理模型试验和数值模拟试验波面吻合良好。
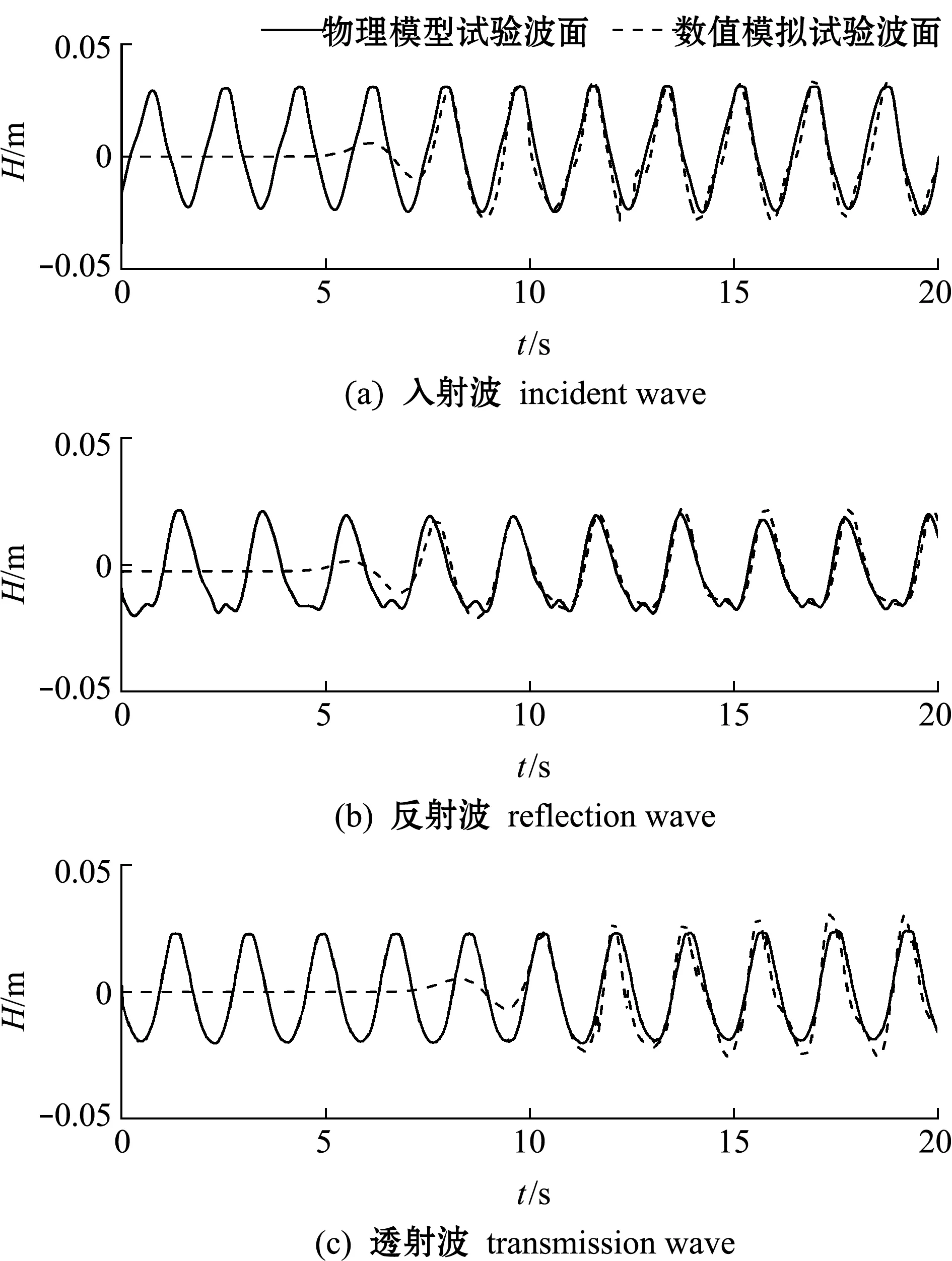
图3 不同波的波面对比
数值模拟采用规则波。利用VOF法获取波面数据,并用下式计算透射系数和反射系数:
Kt=Ht/Hi,Kr=Hr/Hi。
(8)
其中:Ht为透射波高;Hi为入射波高;Hr为反射波高。
图4为波高H=0.13、0.04 m,透射系数试验中前挡板入水深度相同而后挡板入水深度不同时,透射系数随相对堤宽(B/L=0.24、0.40、0.51)的变化,数值模拟和物理模型试验透射系数吻合良好,随着相对堤宽的增大,透射系数不断减小。
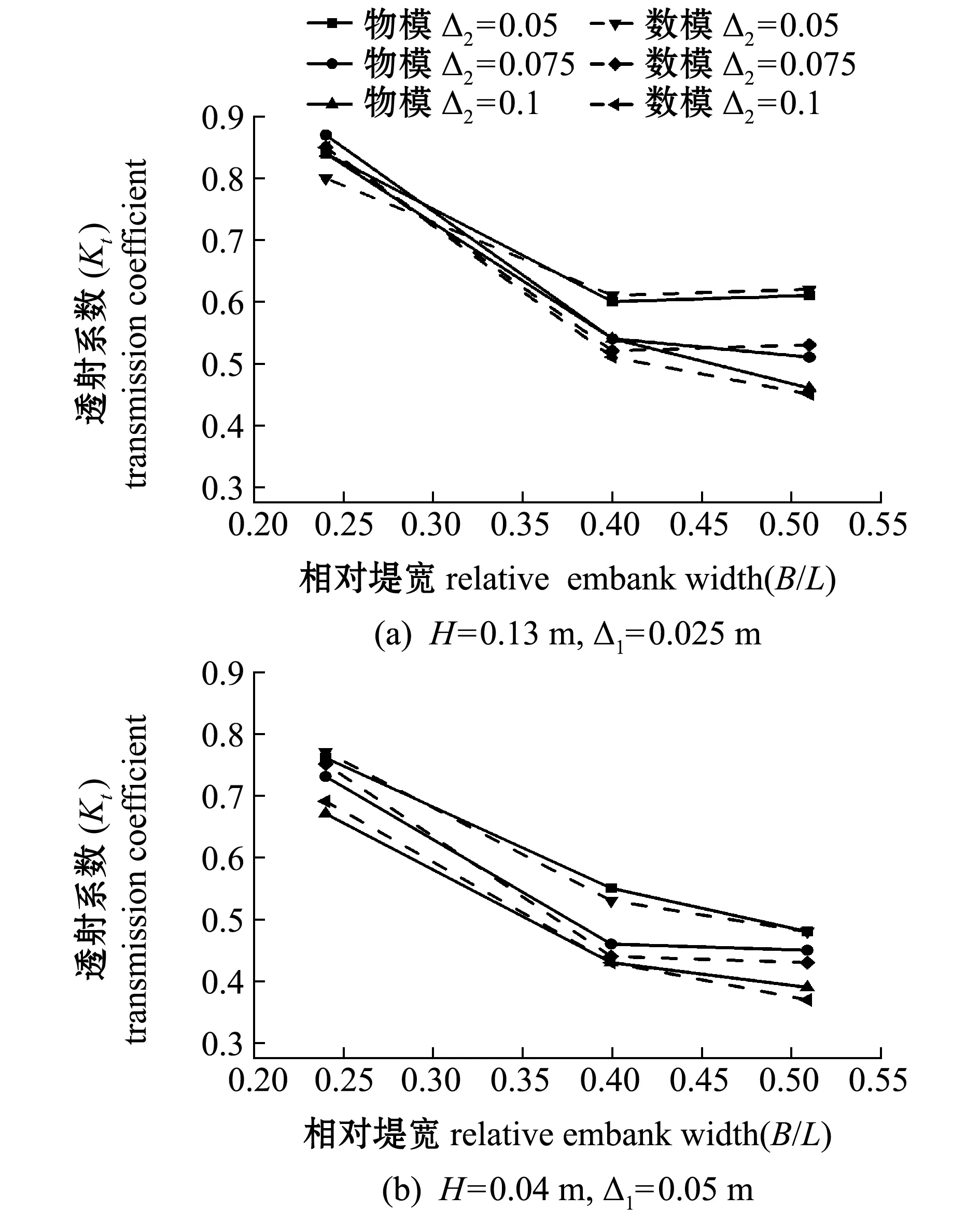
图4 相对堤宽对透射系数的影响
图5为T=1.8、1.2、1.0 s,d=0.3 m时,物理模型试验和数值模拟试验中透射系数随相对波高(H/d=0.13、0.20、0.27、0.33、0.43)的变化,透射系数吻合良好,随着相对波高的增大透射系数不断减小。当H/d<0.3时相对波高对透射系数影响较大,当H/d>0.3时相对波高对透射系数影响较小。可见,挡板式透空堤对大波高波浪掩护效果更好。
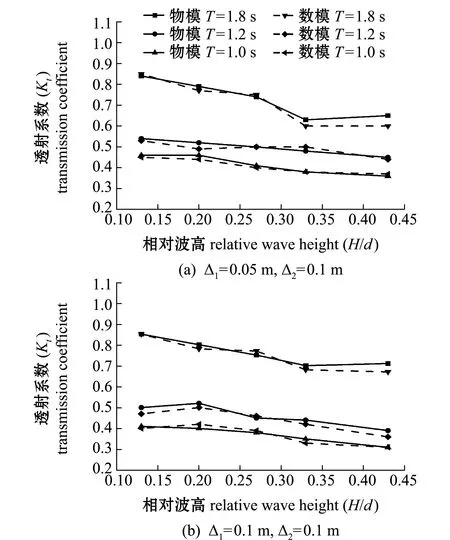
图5 相对波高对透射系数的影响
3 数值模拟试验
3.1 相对堤宽对透射系数的影响
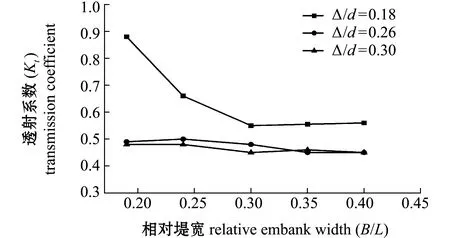
图6 相对堤宽对透射系数的影响
3.2 挡板相对入水深度对透射系数的影响
图7为前后挡板相对入水深度(Δ/H=0.5、1.0、1.5、1.9、2.3)对透射系数的影响,试验采用数值模拟的方法,前后挡板入水深度相同的条件下对结构进行了无量纲化处理,由于规范规定相对堤宽应大于0.25L,故在进行Δ/H的研究时,防波堤的堤宽取0.25L。由图7可见,随着Δ/H的增大,无论是长周期波浪还是短周期波浪,透射系数均减小。当挡板入水深度Δ小于1倍入射波高(H)时,透射系数减小的幅度较大,当挡板入水深度大于1倍波高时,透射系数下降幅度逐渐减小。在1倍波高后再增加挡浪板入水深度,周期为1 s的短周期波透射系数几乎无变化,且透射系数在数值上也较小,而周期为1.8 s的长周期波透射系数有略微的减小,这说明双侧挡板入水深度的增大对于短周期波浪的削减效果明显且效果优于长周期波。图7中Δ=1H为明显拐点,这一现象也符合波能主要集中在水面上下1倍波高附近的理论。
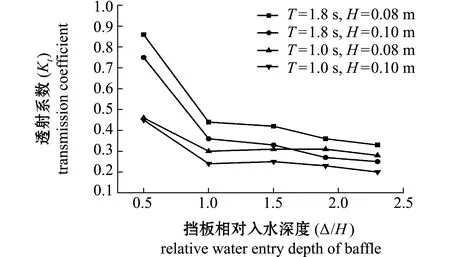
图7 相对入水深度对透射系数的影响
3.3 流场分析
图8为T=1.8 s、H=0.13 m一个周期内前后垂直挡板入水深度不同时,透空堤流场的变化。从图8可见:t=0时,波浪开始与结构物作用时波浪微小,入水深度大的后挡板对水体扰动明显强于前挡板;t=1/4T时,前垂直挡浪板迎浪方向的水体处在波峰位置,此时结构物后方水体增高,前挡板挡住部分水体;t=3/4T时,挡板迎浪方向的水体开始进入波谷状态,波谷和结构物反射回的波开始作用,反射最大;t=1T时,挡板前水体进入波谷后期,消浪室内水体较高。这表明,堤宽较大时会使波浪在挡板间发生紊乱从而使部分能量耗散掉,挡板入水深度增大时也会使挡板对水体的扰动面积加大从而消耗波浪更多能量,故透射系数减小。
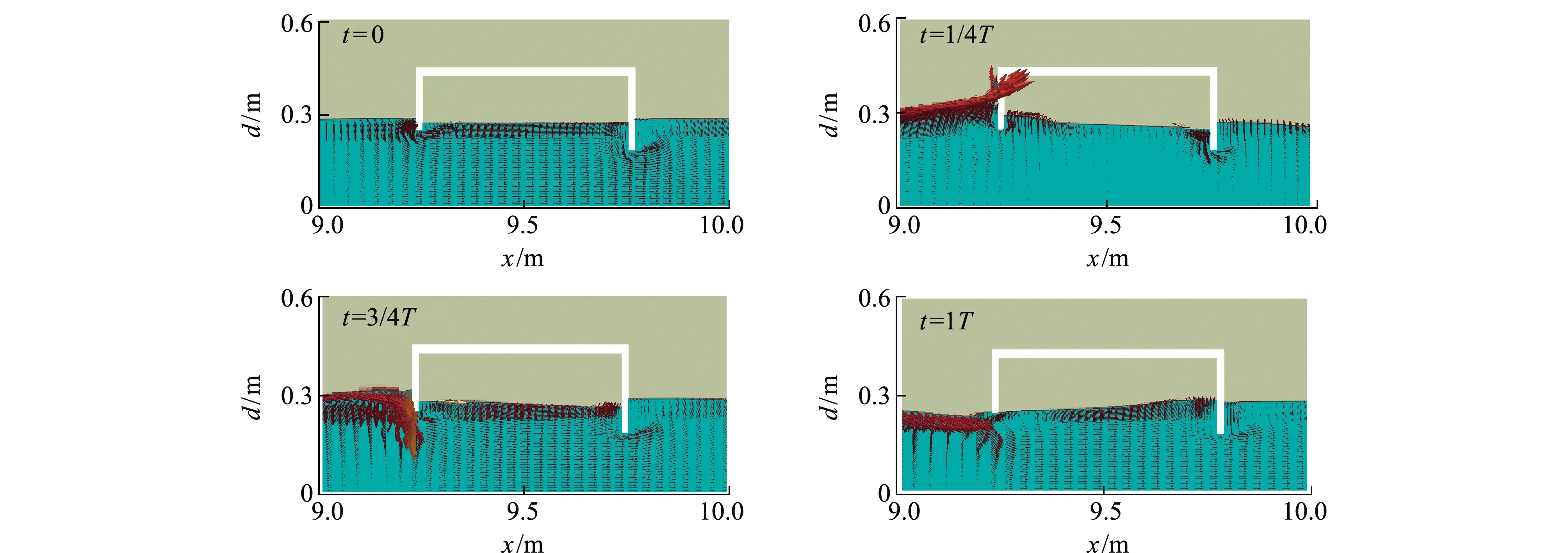
图8 T=1.8 s、H=0.13 m一个周期内透空堤的流场图
4 讨论
4.1 OpenFOAM数值模拟方法的优势
本研究中主要采用OpenFOAM开源软件进行数值模拟,且经物理模型试验验证了其有效性。以前较多类似研究大多采用物理模型试验,冯卫兵等[15]通过物理模型试验探究了相对堤宽和相对波长等对双挡板透空堤透射系数的影响,范骏等[16]通过物理模型试验探究了相对堤宽和挡板入水深度对透射和反射的影响,但是物理模型试验费用较高,试验中不易改变模型结构,有较大的局限性。OpenFOAM软件基于 CFD原理,应用灵活、方便且准确,可以根据自己的需求编写代码开发求解器。李钦等[17]基于OpenFOAM中的InterDyMFoam求解器模拟对比了开孔及无孔板式防波堤的消浪状况,证明开孔板式消浪性能更优。本研究中采用的求解器为项目组前期开发的DutFoam求解器,经证明有效[18],在试验中可以设置不同的水槽长度、水深、波高、波长及周期等试验参数,可模拟任何需要的结构模型,并能清晰地观察整个数值模拟的过程。
4.2 透空堤透射系数及流场变化机理
近年来,中国越来越重视保护海洋,提出了建设绿色港口的理念,传统的实体式防波堤存在不利于水体交换且对港内水环境影响较大的缺点。透空式防波堤下部透水,虽有利于港内水域环境,但与实体式防波堤相比其掩护效果较差。目前对挡板式透空堤的研究资料较少,故研究挡板式透空堤在工程上有重要意义。本研究中主要探究了透空式防波堤相对堤宽和挡板相对入水深度在工程应用时的合理取值范围,并通过物理模型试验和数值模拟试验对透射系数展开了全面研究。冯卫兵等[15]和范骏等[16]虽均对双挡板透空式防波堤透射系数进行了研究,但其只探讨了相对波高、相对波长等工况对透射系数的影响,未研究其在工程应用时的具体合理取值范围和分析透射系数变化的机理。本研究中补充研究了相对堤宽和挡板相对入水深度的合理取值范围,并利用数值模拟分析了透空堤流场的变化,提出相对堤宽B/L取值范围应为0.25~0.35L,挡板相对入水深度应大于1.0H。规范中规定相对堤宽B/L应大于0.25L,这与本研究中得出的相对堤宽取值范围一致,且本研究中更加准确地提供了相对堤宽的取值范围,波浪理论中提出波能主要集中在水面上下1倍波高附近,此观点与本研究中总结的挡板相对入水深度取值范围相吻合,证明了本结论的正确性。
通过观察透空堤流场图可见,前后挡板及上挡板形成了消浪室,当波浪进入消浪室内会在其中来回震荡,波浪发生紊乱,当相对堤宽增大时震荡空间变大,波浪消耗能量变多,但当相对堤宽增加到一定值时,波浪震荡趋于稳定,使得波浪耗能也稳定,透射系数不再大幅度减小。挡板相对入水深度不同时,对波浪的扰动深度和面积也不同,挡板相对入水深度增加时扰动面积增大,从而使波能消耗增加,透射系数减小,但当挡板入水深度增加到一定时耗能趋于稳定,透射系数不再大幅度减小。本试验是实际工程的拓展研究,所得结论均可应用在实际工程中。由于前后双挡板透空堤透射系数相比实体防波堤透射系数相对较大,今后的研究中可以改善其透空堤结构,增大结构与波浪作用时波浪的耗散能量,使透射系数更小,增加港内水体稳定性。
5 结论
1)随着相对堤宽B/L的增大,透射系数减小,当B/L大于0.35时透射系数趋于稳定,结合规范给出了实际工程上相对堤宽的适宜范围为0.25~0.35L。
2)随着挡板相对入水深度Δ/H的增加,透射系数减小,当挡板相对入水深度大于1.0H后透射系数趋于稳定,在实际工程上可将挡板相对入水深度设为大于1.0H。
3)透空堤相对堤宽较大时,或挡板相对入水深度增大时,均会使波浪耗散部分能量,从而减小透射系数。这说明相对堤宽和相对入水深度是透射系数减小的主要影响因素。

