挡土墙抗滑键抗滑作用研究综述

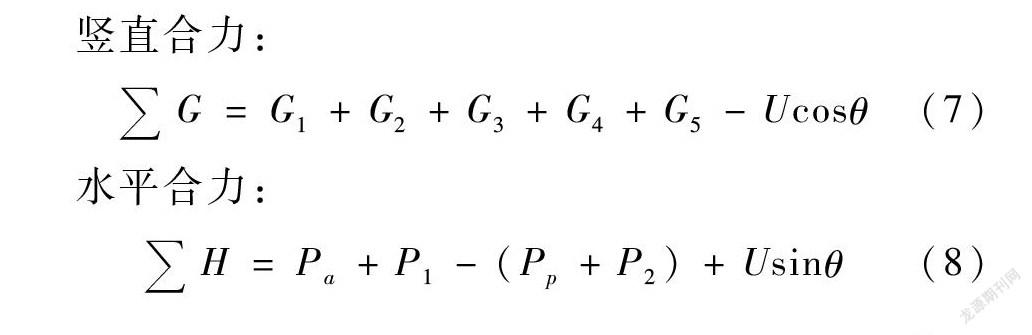
摘要：基于国内外挡土墙抗滑键的研究成果，讨论了挡土墙设键对提高抗滑稳定性的影响，介绍了抗滑键作用机理及国内外抗滑键设计计算方法。各抗滑键设计方法差别较大，多数在底板中部或墙踵附近设键，但现场观测却发现正常工作荷载下键设在底板中部时键前被动土压力远小于设计预想，而在墙趾设键的抗滑作用则得到现场观测和模型试验的验证。基于对抗滑力仅与地基土抗剪强度有关的理解，根据传统的极限平衡法推导了墙趾设键挡土墙的抗滑稳定计算公式，该公式与《水工挡土墙设计规范》中底板向填土方向落深倾斜的抗滑稳定计算公式本质一致。对于护岸挡土墙，在墙趾设键可相应抬高底板，改善基础应力，还可起到改善基底扬压力和防冲作用，因此在护岸工程中得到广泛应用。

关 键 词：挡土墙; 抗滑键; 抗滑穩定; 墙趾; 墙踵

中图法分类号： TU476+.4

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.04.022

0 引 言

挡土墙抗滑键，也称为阻（防）滑键，国内工程界一般多称为凸榫（如《铁路路基支挡结构设计规范》[1]《水闸设计规范》[2]）。水工专业对位于底板两端的抗滑键常称为齿墙（如《水工挡土墙设计规范》[3]）。也有部分专家学者把抗滑键称为齿坎，但在水工上齿坎一词常用于齿状消能构造设施，因此，笔者认为对于水工挡土墙抗滑键不宜称为齿坎，以免造成概念混乱。下文中“齿墙”指位于底板两端的抗滑键，“凸榫”指位于底板墙踵和墙趾以外部位的抗滑键。

水利工程中的挡土（水）建筑物，当位于软弱地基中时，常通过设置齿墙来满足防冲抗渗目的（如水闸底板的上下游端一般都设有齿墙），但其抗滑作用往往不予考虑，设计时仅作为安全储备。《水工挡土墙设计规范》[3]建议：“土质地基上的挡土墙底板底部宜设置齿墙，齿墙深度可采用0.5～1.0 m”（4.2.10）;当挡土墙基底面抗滑稳定安全系数计算值小于允许值时，建议采取的抗滑措施包括“适当加深基底齿墙的深度”（6.3.13）。当沿岸墙、翼墙基底面抗滑稳定安全系数计算值小于允许值时，《水闸设计规范》[2]建议采取包括“在基底增设凸榫”等抗滑措施（7.4.7）。可见，抗滑键的设置有助于提高挡土墙的抗滑能力，而不必增加其底板宽度。不少文献[4-7]也介绍了利用抗滑键提高挡土墙抗滑稳定性的工程案例。但设键后，抗滑键到底能提供多大的抗滑力，设计时应如何考虑，在工程设计中尚无统一的认识，国内规范对此也未作出规定。可见有关这种结构的设计理论还很不成熟，导致经常将抗滑键视为构造措施，不考虑其对结构稳定性所起的作用或仅作为安全储备[8]。因此，正确地分析理解抗滑键对挡土墙抗滑的作用，对提高现有的工程设计水准有着积极的工程意义。

1 抗滑键提高挡土墙抗滑稳定作用讨论

根据传统分析方法和工程师在实践中使用的参数值，所需挡土墙底板宽度通常是由水平滑移所决定。为减少挡土墙底板宽度，大多数设计者使用抗滑键。在岩石基础或坚实土基上设键是很有利的，所提供的阻力变成是将键从底板剪断所需的力。美国海军设施工程司令部设计手册《基础及土工构筑物》[9]（DM-7.02，NAVFAC 1986）建议刚性挡土墙“当地基为岩石或非常坚硬的黏土时，可以在基础下面设置一个键来提供额外的抗滑力。”实际上，对于岩石地基，挡土墙底板与地基岩面犬牙交错，岩基与混凝土底板之间的摩擦系数比较大，一般不存在抗滑问题，如美国规范《挡土及防洪墙》[10]（EM 1110-2-2502）就指出挡土墙“对土基可设键以提高抗滑力，对岩基通常不设键。”但在软弱地基设键究竟对挡土墙抗滑能起到多大的作用，还是存在不同认识。

国内设键挡土墙文献大多数均认为键的抗滑作用明显。屠毓敏等[11]以一系列现场试验为基础，研究在墙趾设键对位于软弱地基中的航道护岸挡墙抗滑稳定性的作用，发现尽管齿墙较短，但对护岸结构的抗滑作用甚大。钱铁柱[4]介绍了防滑凸榫挡土墙在北京马草河治理工程中的应用实例，认为采用防滑凸榫挡土墙可以大幅度提高抗滑能力，减小挡土墙断面，节省工程投资。赵乃志等[12]通过对沈大高速公路某段带凸榫结构的重力式挡土墙进行力学分析，也认为凸榫可以显著提高挡土墙抗滑力。陈妙福等[5]介绍了杭申线崇福市河道改线工程中采用齿墙式护岸优化结构后，不仅保证了护岸的顶部位移与沉降量满足规范要求，而且为整个工程节约了大量资金。杜永峰等[6]通过挡土墙其他防滑措施的对比分析，认为防滑凸榫具有构造相对简单、工程量相对较少、防滑效果佳、经济效果好等优点。

国外文献则有所不同，有些工程师并不认为抗滑键能按预期起作用，如Elman等[13]就认为只有对非常坚硬的地基土键才能充分发挥作用，他们提出了一种倾斜基础的替代方案，即挡土墙基底面由墙趾往墙踵向下倾斜。Horvath[14]通过对砂基上不同底板型式（平底板、倾斜底板和抗滑键分别位于墙趾、墙身下部、墙踵3种不同设键情况）钢筋混凝土悬臂挡土墙进行数值模拟分析发现：不同底板型式的挡土墙荷载-位移、荷载-旋转曲线很相似，特别是在典型负荷水平处于主动状态到静止状态的墙后土压力范围内时;只有在更高的荷载作用下在墙踵设键才稍微显示出优势。Horvath认为，通常平底板挡土墙之所以比带键挡土墙抗剪力小的原因是大多数设计者选取保守的基底摩擦系数（或内摩擦角），而Horvath在研究中则选取更贴近真实的参数;考虑到设键增加的工程量，抗滑键并没有优势，不如研究如何采用更合理的不保守的土-混凝土底板摩擦参数。Camp等[15]通过大爆炸算法对带键和平底板悬臂钢筋混凝土挡土墙进行优化设计，发现带键挡土墙成本略有下降：当以底板范围内的堆载（0～40 kPa）为函数时，带键挡土墙的优势不明显;当以墙后填土地面倾斜角（0～25°）为函数时，带键挡土墙比没有键的挡土墙成本平均节约4%左右;当以墙后填土内摩擦角（28°～36°）为函数时，带键挡土墙比没有键的挡土墙成本平均节约3%左右。总的来说，底板设键的挡土墙往往比那些没有键的挡土墙更为划算。Gandomi等[16]对一4.5 m高的挡土墙进行基于进化算法的优化设计，研究抗滑键的作用，认为在荷载小时基底设键是没有意义的;在荷载大时，基础设键可以作为一种更优的设计选择。F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

对位于软弱地基的挡土墙，在水平推力作用下，挡土墙可能连同地基发生深层滑动。刘金龙等[17]基于强度折减有限元法，通过变换参数与改变挡土墙结构型式，分析键的作用机理与影响因素。他发现：软弱地基上设键挡土墙的滑裂面为一通过底板及键后缘的近似圆弧面;键的作用实际上是使土体的破裂面向更深更远的地方发展，类似于锚杆、抗滑桩的作用;随着键长度的增加，挡土结构物的安全系数增大;键布置在墙踵更容易影响与改变滑裂面的位置，从而使挡土结构物的稳定性得以提高。

2 抗滑键作用机理

挡土墙必须提供足够的抗滑力以保证抗滑安全，挡土墙的抗滑力主要是由墙底和基础材料的摩擦提供，部分是由挡土墙墙前土体可能产生的被动土压力提供。如果發现挡土墙抗滑安全性不足，则可在底板下设置抗滑键，设键的主要目的是增加由键高度产生的额外的被动土压力。根据挡土墙相对于填土的位移方向和大小，将产生3种不同性质的土压力，分别为静止土压力、主动土压力和被动土压力。其中主动土压力最小，被动土压力最大。根据朗肯土压力理论，对于内摩擦角φ=30°的回填砂土来说，被动土压力系数是主动土压力系数的9倍。可见，如能充分利用被动土压力将是非常有效的一种抗滑手段。

一般认为，极限土压力的发生条件与墙体位移、墙体结构型式、地基条件、填土种类、填土密实度等因素有关，其中最主要的因素是墙体相对填土位移。表1列出美国《基础工程手册》[18]中所给出的数值可供参考，H为挡土墙高度。

由表1中数值可见，产生主动土压力所需位移量较小，而产生被动土压力所需位移量则大得多。对大多数挡土墙来说，在墙后土压力或其他荷载作用下往往会产生离开填土方向的位移或偏转，墙背所受土压力较接近主动土压力，因而中国现行设计标准对此大多采用主动土压力进行设计[19]。而产生被动土压力的位移值比较大，特别是当墙体发生绕墙底转动时（软弱地基挡土墙容易产生的位移模式）产生被动土压力所需位移值更大。挡土墙与前后土体既相互作用又互为一体，墙后填料作用于挡土墙呈主动土压力状态时，墙前土体的作用难以完全进入被动状态，其实际作用力比计算的土压力小，因此通常为保证抗滑稳定安全，设计计算时一般不考虑墙前被动土压力的作用，只有在埋置较深（埋深大于1 m）且能确定不受冲刷或其他扰动破坏时才计入部分被动土压力值。如《铁路路基支挡结构设计规范》[1]规定墙前土体抗力可取1/3被动土压力值，《公路路基设计规范》[20]规定墙前被动土压力对结构有利时分项系数为0.30。多数设计将键设在底板中部或墙踵附近，认为由于被动土顶部的竖向压力较高可以调动更大的被动土压力，不对键前被动土压力进行折减或折减不多，据此计算的抗滑键作用很明显。

此外，抗滑键的作用还体现在增强了土体破坏面的局部加深，挡土墙基础滑移破坏面将下移到键底面，使得滑动面只有在土体中发展。通常在设计计算时，挡土墙基底面与土质地基之间摩擦角φ0值和黏结力c0值要小于地基土的摩擦角φ和黏结力值c，《水工挡土墙设计规范》[3]（6.3.8）规定：对于黏性土，φ0=0.9φ，c0=（0.2～0.3）c;对于砂性土，φ0=（0.85～0.9）φ，c0=0;φ和c为室内饱和固结快剪试验测得的内摩擦角（°）和黏结力（kPa）。当滑动面发生在地基土内部时，计算采用的指标可直接采用地基土摩擦角φ和黏结力c，由此计算的安全系数值有所提高。

3 抗滑键设计计算方法

抗滑键设计包括键位置、宽度和深度等，而土压力计算与键位置、破坏面假定等密切相关。下面介绍国内外典型的抗滑键设计计算方法。

3.1 国内凸榫设计

国内不少设计手册[21-22]和参考书[23-24]主张在墙底中部某一位置设置凸榫，并给出位置确定和凸榫高度hT的估算方法：为了增大凸榫前被动阻力，应使凸榫前被动土楔不超出墙的前趾;同时，为了防止因设凸榫而增大墙背的主动土压力，应使凸榫后缘与墙踵的连线同水平线的夹角不超过地基土内摩擦角φ，因此，应将整个凸榫置于通过挡土墙前趾并与水平线成45°-φ/2角线和通过墙踵与水平线成φ角线所形成的三角形范围内。凸榫的高度hT也要求不超出以上三角形范围，如图1所示。凸榫宽度可按满足截面弯矩和剪力要求确定。凸榫前的被动土压力强度pp按下式作近似计算：

pp=12（p1+p3）tan2（45°+φ2）（1）

式中：p1，p3为墙趾和凸榫前缘处基底压力强度。

通常挡土墙的抗滑验算不考虑墙趾以上土体的抗滑作用，而将它作为安全储备。由图1可知，加凸榫后榫前被动土压力与榫后挡土墙基底摩擦力共同抵抗挡土墙滑移，榫前土体与挡土墙基底摩擦力不再计入，因此可得到加凸榫挡土墙的抗滑稳定性验算公式：

Kc=Pp+0.5（p2+p3）（B-BT1）fPH（2）

式中：Pp为凸榫前被动压力，Pp=pp hT;PH为墙后土压力水平分量;B为挡土墙基底宽度;BT1为凸榫前墙基底宽度;f为挡土墙基底摩擦系数。

《铁路路基支挡结构设计规范》[1]条文说明7.2.3指出：“由于被动土压力的存在，在进行滑动稳定性验算时，平衡作用组合中不考虑BT1段（榫前底板段）的摩擦力”，这样一来，必然导致“从计算公式来看，凸榫位置越靠近墙趾（只要墙前能形成被动土压力），抗滑能力越大”，这说明凸榫设计计算方法是有问题的。最大的问题是采用由式（1）计算的榫前被动土压力强度，其值远大于墙趾前面的土压力值。实际可能的破坏面存在于沿键底端和墙趾的斜面与沿键底端水平面之间，合理的做法是假设几个可能滑动面计算出相应的安全系数，取其小值作为挡土墙的抗滑稳定安全系数。用某些商业软件设计挡土墙，对比是否设置凸榫，会发现设置凸榫的抗滑效果很明显，如果设计者不加以分析，那么容易得出虚假的安全系数，导致挡土墙达不到设计所需的安全度。

3.2 英美等国家及地区带键挡土墙设计F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

3.2.1 假设挡土墙沿键底水平面滑动

（1） 底板设键后墙前被动土压力从键底部起算，墙后土压力仍然从墙底板底部起算。

对于钢筋混凝土悬臂挡土墙，在工程实践中常将键放在墙体之下，基底抗滑键靠近墙身使墙身的钢筋可以直接进入键内，以方便施工。由于键离墙踵较远，设计计算时墙前被动土压力从键底部起算，墙后土压力仍然从墙底板底部起算。如《基础及土工构筑物》[9]规定刚性挡土墙的抗滑稳定分析，不考虑墙前被动土压力，当抗滑稳定安全系数不满足要求时，在基础下面设置一个键来提供额外的抗滑力，如图2所示，假设从墙趾底部起算的墙前埋深h，键高hT，键前被动土压力平均强度为

pp=（γh+12γhT）tan2（45°+φ2）（3）

砂性土：

F=fG+ Pp（4）

黏性土：

F=tanφ0G+c0（B-BT1）+cBT1+ Pp（5）

挡土墙的抗滑稳定安全系数

Kc=F/PH（6）

式中：G为作用在挡土墙基底上全部垂直于水平面的荷载，包括图2键前原状土块的重力;BT1为键前墙基底宽度;c为地基土的黏结力;φ0，c0为底板与地基土之间的摩擦角和黏结力。

美国设计手册《挡土墙设计基础》[25]建议抗滑键设置在墙底板中心附近，键深小于1/4挡土高度且不大于2英尺，键宽在12～18英寸之间。计算时墙后土压力仍然从墙底板底部起算，墙前被动土压力从键底部起算，挡墙底板顶部以上的被动土压力不考虑其作用，墙前被动土压力设计值只取计算值的50%。

（2） 被动土压力、主动土压力都从键底部起算。

显然，在设键位置离墙踵较近时不考虑键深引起的墙后土压力是不合适的。澳大利亚《钢筋混凝土砌块悬臂式挡土墙设计和施工指南》[26]推荐把键设置在墙踵，认为这样设置简化钢筋布置，方便施工。计算时规定水平力均从键底部起算。

3.2.2 综合考虑两种破坏机理确定最小抗滑安全系数

美国加州规范《桥梁设计规范：第5节挡土墙》[27]规定：对于底板设键的挡土墙，当键深度大于键后侧面到墙踵的距离时，墙后土压力必须从键的底高程开始计算。在结构寿命期内，如果能保证墙前基土不被移除或冲刷，可考虑底板和键前面被动土压力的作用。对于带键的挡土墙，水平和倾斜的滑动面都必须考虑，以确定最小抗滑安全系数。

英国规范BS 8002：1994《挡土结构实用规程》[28]规定键应位于底板后半部，如图3所示，墙后主动土压力从键底部起算（即应考虑作用在EF额外的主动土压力），分别计算沿BCD破坏和沿ACD破坏两种破坏形式的抗滑安全系数，取其小值作为挡土墙的抗滑稳定安全系数。如图3所示设键挡土墙，当出现沿AC滑动情况，键埋深较浅且设置位置比较靠近墙趾时，采用抗滑键对提高挡土墙抗滑稳定性的帮助不大;而键的位置越靠近墙踵，抗滑距离就越大，因此，J.E.波勒斯在其编著的《基础工程分析与设计》[29]中认为最好的设键位置是在踵部，此位置不但由于向上倾斜的面而增加了一个附加分力，而且抗滑距离也稍大些。但正如香港《挡土墙设计指南》[30]所提醒的：“在选择键位置时，考虑最大滑动阻力目标的同时应权衡破坏临时开挖稳定性的风险，当键的位置太靠近墙踵时可能发生这种情况。”

4 现场观测和模型试验

（1） 现场观测发现凸榫前土压力远小于设计预期。

Bentler等 [31]对一墙身高7.9 m（从底板底部起算墙高8.5 m，墙身下部设置一0.3 m×0.3 m的凸榫，墙前土埋深从底板底部起算有1.5 m）的钢筋混凝土挡土墙进行现场观测（应力仪器埋设布置见图4）。记录随墙后回填过程的测点应力变化过程，发现底板趾前（埋深1.2 m处）的土压力比凸榫前的土压力大得多（见图5），表明墙趾比凸榫提供更多的滑动阻力。EPC_趾记录的墙趾前最大土压力约为67%的理论被动土压力，而EPC_键记录的榫前土压力则小于设计值的10%，表明在底板设置凸榫对正常工作负荷的悬臂挡土墙作用不大。Bentler对此的解释是：由于墙前土埋深比墙后面的小得多，底板墙趾前面土体产生被动土压力所需要的位移量也要小于凸榫位于墙身与墙踵之间任何位置产生被动土压力所需要的位移量[31]。考虑到实验观测到底板墙趾前可观的抗滑力，只要能保证墙前土不会被扰动破坏，那么在计算抗滑安全系数时考虑墙前土的抗滑作用是合理的。

由表1数值可知：挡土墙不管是平移还是绕墙底转动，产生主动土压力所需墙顶位移是一样的，但产生被动土压力的位移值则差别甚大。对于砂土填料，绕墙底转动达到被动土压力状态所需位移是平移模式的两倍以上。对于土基擋土墙，地基刚度越小，越容易发生绕墙底转动;基底设键后，转动点一般位于键底部，此时，当墙后填料作用于挡土墙呈主动土压力状态时，键前土体的位移量远小于产生被动土压力所需的位移值，其实际作用力也因此远小于被动土压力计算值。

（2） 现场和室内模型试验证明墙趾设键对提高挡土墙抗滑能力作用明显。

俞亚南等[32]在淤泥质土地基上对高2.8 m、底板宽1.8 m厚0.4 m的单宽长度挡土墙进行一系列现场试验，研究发现：当墙趾设键（齿墙）时，挡土墙的抗滑稳定性有大幅度的提高，在试验齿长（1.0 m）范围内，其抗滑力随着齿长的增加近似地呈线性增加，就摩擦系数而言，设0.7 m长的键比无键的大1倍。由现场试验结果，根据工程设计中的摩擦系数概念，可以求得混凝土与淤泥质黏土和淤泥质粉质黏土之间的摩擦系数分别为0.528和0.484，这远大于规范所规定的数值（水利规范规定软弱黏土摩擦系数值为0.20～ 0.25，《建筑地基基础设计规范》规定可塑性黏土摩擦系数值为0.25～0.30）。可见，设计采用的摩擦系数值确实过于保守。对比土压力的实测值和理论值可见：当齿长较长时，其相对误差较大，且理论值大于实测值;当齿长较短时，实测值与理论值相当。齿长愈长，则齿墙下部的齿前土压力发挥得愈不充分，故实测土压力比理论值要小。由试验和理论分析可得：当水平推力达到极限值时，齿后的主动土压力为0。F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

屠毓敏等[33]通过室内模型试验发现：位于软弱地基中的无齿挡墙，当墙重较小时，极限抗滑力与基底压力分布无关。但当墙重较大时，基底压力分布对极限抗滑力产生较大的影响，此时表现为倾斜荷载作用下的地基稳定性。当挡土墙在前趾设置齿墙时，由于齿墙的嵌固作用，可有效地提高地基的承载能力，从而进一步提高挡土墙的抗滑作用，此时齿墙起着抗滑和地基加固双重作用。为此，在软弱地基中建造重力式挡土墙时，应优先考虑设置齿墙。当带齿挡墙达到基底滑动破坏时，齿前的被动土压力值比朗肯被动土压力值要小，存在着折减系数，其值可取0.7左右，而基底抗滑力完全可按土的抗剪强度理论计算，土体强度指标宜取固结不排水剪或固结快剪强度指标。

5 墙趾设键挡土墙

5.1 最佳设键位置

由前面对各抗滑键设计方法的介绍可知，目前对于设键最佳位置存在不同看法。当键位于底板后半部，特别是位于墙踵附近时，墙后土压力从键的底高程开始计算，对于软弱地基还有可能出现通过键底前缘往墙前倾斜向上的斜面滑动破坏情况;当键位于墙趾附近时，墙后土压力仍从墙底板底部起算，即设键没有增大墙后土压力，只是增加了键前被动土压力，这样看来在墙趾设键是个好的选择。然而多数规范和设计手册并不建议在墙趾设键，主要是担心开挖可能会使墙前土被移走，导致土的侧向阻力很难被调动起来，影响键功能正常发挥。同时，对位于底板后半部的抗滑键，通常认为由于被动土顶部的竖向压力较高而可以调动更大的被动土压力。对于在国内工程界得到广泛应用的凸榫设计方法，榫前的被动土压力主要是利用了基底产生的附加应力，由此计算出的凸榫前被动土压力比较大，凸榫产生的抗滑效果很明显。但Bentler等 [31]现场观测发现凸榫前的土压力远小于设计预期，墙趾比凸榫提供更多的抗滑动阻力。而俞亚南和屠毓敏[32-33]的现场试验和室内模型试验均表明墙趾设键对提高挡土墙抗滑能力作用明显。

一些学者经过研究也认为墙趾是最佳设键位置。俞亚南等[34]采用D-P弹塑性薄层单元模型数值模拟方法，研究带键挡土墙的抗滑稳定性，认为键位置对挡墙的极限抗滑力存在着一定的影响。从极限抗滑力来看，键在墙踵和底板中间的挡墙差异不大，键在墙趾的挡墙极限抗滑力要小些。但从变形情况来看，在同样推力下，键在墙踵和底板中间的挡墙的位移比键在墙趾的挡墙大些，这与基底面水平推力绕键底端产生的转动变形有关。为减少挡墙的水平位移，对于具有一定黏聚力的黏土地基上的带键挡土墙，将键设置在墙趾更为合适。Nisha等[35]利用Plaxis软件分析悬臂挡土墙抗滑键位于不同位置（墙趾、墙身下部和墙踵）时的作用，发现键位于墙趾时效果最好，键位于墙踵时效果最差;而且安全系数随着键深度的增加而变大。吴周明等[36]运用传统的极限平衡法对挡土墙抗滑键作用效果的影响因素及影响程度进行研究，认为墙趾处是最佳的设键位置，同一尺寸的抗滑键结构离墙趾距离越大，挡土墙的抗滑动稳定系数越小，抗滑键设在墙踵处效果最差。

5.2 斜坡挡墙的最佳设键位置

对修建于斜坡上的挡土墙，当键设在墙踵时，增加了开挖边坡的高度，从而增大了破坏临时开挖稳定性的风险，对于软弱地基更是如此。为了减小临时开挖稳定风险，将不得不放缓开挖边坡或采取支护措施，从而增加开挖工程量或支护费用。而在墙趾设键，则可以相应抬高底板，减少开挖土方;降低挡土墙高度，节省挡土墙材料，对于软弱地基还可节省或减小地基处理费用。对于河道护岸挡墙，在墙趾设键可起到截水墙改善基底扬压力分布、减小渗流梯度的作用，对底板下部地基土还可起到防冲保护作用。

在杭嘉湖地区广泛应用的挡板式护岸结构，就是出于防止地基土体淘刷目的，在不断总结实践经验的基础上形成的[37]。挡板式护岸结构分为两大部分，下部是混凝土Γ型底座，上部是直立的浆砌块石挡土墙。所谓的“挡板”实际上就是在基础底板前趾设置深入到岸坡设计最低冲刷线以下一定安全富裕度用以防冲保土的齿墙，而护岸底板基础高程一般稍低于常水位，齿墙的深度一般大于1/2底板宽度，齿墙厚度相对单薄呈板状。工程实践表明，挡板式护岸具有如下突出的优点：① 挡板（齿墙）面水且深入土中，可防船行波冲刷，避免岸坡塌方;② 抗滑性能好，岸墙下部混凝土Γ型底座能较好地抵抗滑移;③ 抗倾性能好，结构重心在岸侧，有利于抵抗倾覆变形;④ 由于底板上抬，减小了挡土墙断面，省工省料，施工简便，经济效益明显，每延米挡板式护岸结构比不带齿墙的岸墙结构节约投资20%～25% [38];⑤ 护岸结构牢固，质量可靠。桐乡市南排工程中有挡板式护岸工程在运行过程中有些区段岸边堆放了1～2 m高的砖堆，其护岸结构也无破坏迹象[37]。1999年在青浦县拦路港最差地质条件下的河岸修建500 m长的试验段（其中浆砌块石低护岸330 m，钢筋混凝土高护岸170 m），工程段竣工后，分别观测墙顶上36個测点的沉降及水平位移，结果发现：低护岸墙顶的最大水平累计位移为1.1 cm，最大累计沉降量为0.9 cm;高护岸墙顶的最大水平累计位移为1.2 cm，最大累计沉降量为0.4 cm，以上观测结果均满足规范要求。试验结果表明挡板式护岸结构是安全可靠的[37]。

5.3 墙趾设键的挡土墙抗滑稳定分析

墙趾设键（特别是深键）挡土墙结构比较复杂，其稳定性分析最好采用有限元法，但对一般设计者来说可能还不具备应有条件。因此，有必要研究计算简便、精度较好的实用简化计算方法。

对于在墙趾设键的挡土墙抗滑稳定分析，离心机试验和有限元分析都验证了最危险滑移面将贯穿键底端与墙踵底端地基土[38]，接近于图6中的AB线。因此，一般均假定结构沿贯穿键底端与墙踵底端的平面滑动，在此基础上对结构进行极限平衡分析。程展林[39]提出一种基于极限平衡理论的稳定性分析方法，土压力均采用朗肯理论计算，被动土压力没有进行折减，没有考虑墙前后水位差的影响。王润富等[38]对作用于齿墙的被动土压力进行折减，即被动土压力实际值为计算值乘以折减系数β，同时令实际滑动面土体的抗滑力T=β（cL+Ntanφ），通过分析结构力的平衡条件可求解出β值，由此求得抗滑安全系数Kc=1/β，但同样没有考虑墙前后水位差的影响。黄荣卫等[40]对程展林分析方法作了改进，考虑了墙前后水位差的影响，但对扬压力的作用方向理解有误。F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

对于抗滑稳定分析中的抗滑力不同规范有不同理解[41]：水利规范认为抗滑力仅与地基土抗剪强度有关;公路部门的设计规范认为滑动面上与滑动方向相反的所有力都是抗滑力，既包括与地基土抗剪强度有关的抗滑力又包括与抗剪强度无关的水平抗滑力（如墙前被动土压力）。前面介绍的抗滑键计算方法均采用后一种理解，但黄岳文[41]经过论证，认为前一种理解更合理，按前一种理解抗滑稳定安全系数实质是基底土抗剪强度折减系数。下面在前人基础上，按水利规范对抗滑力的理解，推导墙趾设键挡土墙的抗滑稳定计算公式。

如图6所示，假定滑动面与AB线吻合。当护岸向前滑动时，墙踵底部至顶面土体对护岸的侧压力为主动土压力，且作用在通过墙踵后侧的垂直面上;挡板前土压力为被动土压力;土压力按规范规定计算;通常AB段坡角小于破裂角，故可不考虑该段主动土压力。将图6所示部分隔离体进行分析（取延长l m计），受到重力G（包括墙体自重G1、底板自重G2、抗滑键自重G3、墙后外伸底板以上土体自重G4、AB段与底板间土体自重G5）、扬压力U（包括浮托力和渗透压力）、主动土压力Pa、被动土压力Pp（取被动土压力计算值的1/3作为设计值）、水压力P1和P2、滑动面上法向压力N、剪应力T的作用，其中：

竖直合力：

G=G1+G2+G3+G4+G5-Ucosθ（7）

水平合力：

H=Pa+P1-（Pp+P2）+Usinθ（8）

考虑到通常规范要求浸水挡土墙填料采用砂性土，式（7）～（8）是按水土分算考虑的。对于黏性土应采用水土合算，此时水面线以下采用土的饱和重度计算总的水、土压力，式中的P1不再考虑，P2仅按墙前水深计算。

设x轴水平向右为正，y轴竖直向上为正，设力F在x轴的分力为Fx，在y轴的分力为Fy。分析AB线以上结构力的平衡条件：

Fx=0，H=Tcosθ-Nsinθ（9）

Fy=0，G=Tsinθ+Ncosθ（10）

求解以上方程组可得：

T=Hcosθ+Gsinθ（11）

N=Gcosθ-Hsinθ（12）

根据莫尔-库仑破坏准则，AB滑动面抗滑力为

Tf =cL+Ntanφ=cL+（Gcosθ-Hsinθ）tanφ（13）

挡土墙的抗滑稳定安全系数：

Kc= Tf /T（14）

把式（11）和式（13）代入式（14），可得：

Kc=cL+（Gcosθ-Hsinθ）tanφHcosθ+Gsinθ（15）

对于砂性土，取c=0，f=tanφ，代入式（15），可得：

Kc=f（Gcosθ-Hsinθ）Hcosθ+Gsinθ（16）

结构安全系数的取值（许用安全系数）是和其所用计算方法以及参数取值方法密切相关的，三者不可分割地组成一个工程安全评价系统。规范对结构安全规定的许用安全系数是与规范规定的计算方法和参数取值方法相对应的。由推导过程可知式（15）和（16）与规范公式本质上是一致的，把式（16）分子的“-”改为“+”，分母的“+”改为“-”，就变成《水工挡土墙设计规范》底板向填土方向落深倾斜的抗滑稳定计算式（6.3.7），两者差别主要是由基底倾斜方向不同引起。只要参数按规范取值方法取值，那么式（15）和（16）就可采用规范规定的许用安全系数。

6 结 论

（1） 现场试验表明：混凝土与地基土之间的摩擦系数远大于规范所规定的数值，设计采用的摩擦系数值过于保守;而且一般设计时不考虑墙前土体的抗滑作用，导致计算得到的安全系数偏小，容易造成抗滑安全度不足的错觉;设键后计算得到的安全系数满足要求，但实际上在设计荷载作用下可能无需设键就已满足要求。因此，通常情况下在正常工作荷载下键的抗滑作用可能没有预期的那么大，只有在挡土墙发生较大水平滑移时键的抗滑作用才能得到充分发挥。

（2） 在墙底设键以提高抗滑力的设计理论还不成熟，存在多种不同的设计方法。其中国内常用的凸榫设计计算方法，利用基底产生的附加应力，计算出的榫前被动土压力比较大，给人凸榫产生的抗滑效果很明显的感觉。但现场观测却发现正常工作荷载下榫前被动土压力远小于预想，凸榫的作用很小。

（3） 键起到的作用与具体设置位置有关。当挡土墙最可能的破坏模式是整体滑动破坏时，在墙踵设键可降低滑裂面位置，从而提高挡土墙稳定性。对于斜坡上的挡土墙，在墙趾设键可相应抬高底板，改善基础应力。对于河道护岸挡墙，在墙趾设键还具有防冲作用。室内模型试验和现场试验均证明在墙趾设键能大幅度提高挡土墙抗滑稳定性;现场观测也表明在正常工作荷载作用下墙前被动土压力可得到有效调动。对在挡土墙基底中部和墙踵设键的现场试验还有待进一步研究。

（4） 基于对抗滑力仅与地基土抗剪强度有关的理解，根据传统的极限平衡法可推导出墙趾设键挡土墙的抗滑稳定计算公式，该公式与《水工挡土墙设计规范》中底板向填土方向落深倾斜的抗滑稳定计算公式本质一致。

参考文献：

[1] 国家铁路局.铁路路基支挡结构设计规范：TB 10025-2019[S].北京：中国铁道出版，2019.

[2] 中华人民共和国水利部.水闸设计规范：SL 265-2016[S].北京：中国水利水电出版社，2016.

[3] 中华人民共和国水利部.水工挡土墙设計规范：SL 379-2007[S].北京：中国水利水电出版社，2007.

[4] 钱铁柱.防滑混凝土凸榫与浆砌石重力挡土墙的联合运用[J].水利水电技术，2003，34（9）：66-68.

[5] 陈妙福，褚明生.内河航道齿坎式护岸结构分析及应用[J].水道港口，2006，27（6）：368-372.F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

[6] 杜永峰，趙广强，李慧，等.防滑凸榫挡土墙的防滑探讨[J].兰州理工大学学报，2007，33（2）：112-115.

[7] 陶源，谢龙，牛兴伟，等.防滑凸榫在重力式护壁码头中的应用[J].现代交通技术，2014，11（5）：67-69.

[8] 唐金忠.水工结构设计常见问题解析[M].北京：中国水利水电出版社，2011：81.

[9] NAVFAC （Naval Facilities Engineering Command）.Design Manual 7.02，Foundations & Earth Structures[R].Washington，D.C.：U.S.Government Printing Office，1986：82-84.

[10] US Army Corps of Engineers.EM 1110-2-2502 Retaining and Flood Walls[S].Vicksburg：US Army Corps of Engineers，1989.

[11] 屠毓敏，俞亚南.齿坎式护岸结构抗滑稳定性分析[J].土木工程学报，2000，33（5）：97-99，106.

[12] 赵乃志，张敏江，才华.带凸榫重力式挡土墙的滑移分析[J].公路交通科技，2005，22（10）：44-46.

[13] ELMAN M T，TERRY C F.Retaining walls with sloped base[J].J.Geotech.Engrg.，ASCE，1987，113（9）：1048-1054.

[14] HORVATH J S.Effect of footing shape on behavior of cantilever retaining wall[J].J.Geotech.Engrg.，ASCE，1991，117（6）：973-978.

[15] CAMP C V，AKIN A.Design of retaining walls using big bang-big crunch optimization[J].Journal of Structural Engineering，2011，138（3）：438-448.

[16] GANDOMI A H，KASHANI AR，ROKE D A，et al.Optimization of retaining wall design using evolutionary algorithms[J].Struct. Multidisc. Optim.，2017，55：809-825.

[17] 刘金龙，陈陆望，王吉利.软弱地基上齿坎式挡土结构物抗滑特征分析[J].西北农林科技大学学报（自然科学版），2012，40（6）：24-229.

[18] H.F.温特科恩.基础工程手册[M].钱鸿缙，叶书麟，等译.北京：中国建筑工业出版社，1983：551.

[19] 中华人民共和国水利部.水工建筑物荷载设计规范：SL 744-2016[S].北京：中国水利水电出版社，2016.

[20] 中华人民共和国交通运输部.公路路基设计规范：JTG D30-2015[S].北京：人民交通出版社，2015.

[21] 铁道部第一勘测设计院.铁路工程设计技术手册瘙簚路基[M].北京：中国铁道出版社，1995：436-437.

[22] 尉希成，周美玲.支挡结构设计手册[M].2版.北京：中国建筑工业出版社，2004：107.

[23] 管枫年，薛广瑞，王殿印.水工挡土墙设计[M].北京：中国水利水电出版社，1996：48-50.

[24] 李海光.新型支挡结构设计与工程实例[M].北京：人民交通出版社，2004：79-80.

[25] HUGH B.Basics of retaining wall design[M].8th ed.Publisher：HBA Publications，Inc.，2010：55-56.

[26] Concrete Masonry Association of Australia（CMAA）.Reinforced concrete masonry cantilever retaining walls-design and construction guide[S].ISBN 0909407495，2003.

[27] CALTRANS.Bridge design specifications：SECTION 5-Retaining Walls [S/OL].[2021-01-21]http：∥www.dot.ca.gov/des/techpubs/bds.html.

[28] BIS Standards Publication.Code of practice for earth retaining structures：BS 8002：1994[S].1994.

[29] J.E.波勒斯.基础工程分析与设计[M].童小东，译.北京：人民交通出版社，2004：608.

[30] Geotechnical Engineering Office.Guide to retaining wall design （Second Edition）[R].Hong Kong：Government Publications Centre，1993：89.

[31] BENTLER J G，LABUZ J E.Performance of a cantilever retaining Wall[J].Journal of Geotechnical and Geoenvironmental Engineering，2006，132（8）：1062-1070.F3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3

[32] 俞亞南，屠毓敏.齿坎式路基挡土墙抗滑稳定性的现场试验研究[J].中国公路学报，2000，13（2）：27-30.

[33] 屠毓敏，俞亚南.齿坎抗滑作用的模型试验研究[J].水利学报，2000（12）：68-71.

[34] 俞亚南，高庆丰.齿坎式挡土结构抗滑稳定性分析[J].浙江大学学报（工学版），2003，37（6）：652-656.

[35] NISHA S，SHIVASHANKAR R，RAVI SHANKAR A U.Role of shear keys in cantilever retaining wall[C]∥Proceedings of Indian Geotechnical Conference，Kochi，2011：627-630.

[36] 吴周明，傅军健.带凸榫挡土墙的稳定性影响因素分析[J].工程建设与设计，2015（10）：67-69.

[37] 姚杰，潘永明，蒋天华.挡板式护岸的结构特征及在平原河网中的应用[J].浙江水利水电专科学校学报，2000，12（3）：30-31.

[38] 王润富，任青文.挡板式护岸结构稳定性分析方法[J].水利水电科技进展，1997，17（6）：18-20，36.

[39] 程展林.挡板式护岸稳定性研究[J].长江科学院院报，1994，11（2）：41-48.

[40] 黄荣卫，翁葆忠.挡板式护岸的设计与施工[J].浙江水利科技，1998（3）：7-10.

[41] 黄岳文.挡土墙沿基底面抗滑稳定计算的讨论[J].人民黄河，2016，38（2）：108-113.

（编辑：郑 毅）

Research review on slide-resistance of shear key in retaining walls

HUANG Yuewen

（Guangzhou Water Engineering Technical Center，Guangzhou 510640，China）

Abstract：

Based on the domestic and foreign research on retaining walls with shear key，the influence of shear key on improving sliding resistance stability of retaining walls is discussed.The mechanism of shear key and its design calculation methods at home and abroad are presented.There are large differences among different key design methods，most of the methods recommend setting shear key at the wall heel or middle of bottom plate.However，field observation found that the passive earth pressure in front of the key that is set at the middle of bottom plate under normal working loads is much less than the design expectation，while the effect of setting shear key at wall toe is verified by field observation and model tests.Based on the understanding that the anti-sliding force is only related to the shear strength of foundation soil，an anti-sliding stability formula for retaining wall with key at toe is deduced according to limit equilibrium method，and this formula is consistent with the anti-sliding stability formula of the bottom slab inclined to the filling direction proposed in Design Specification for Hydraulic Retaining Wall.For the retaining wall of revetment，the key located at wall toe can not only elevate the bottom plate and improve the foundation stress，but also alleviate base uplift pressure and improve the scour resistance，so it is widely used in the revetment engineering.

Key words：

retaining wall;shear key;anti sliding stability;toe of retaining wall;heel of retaining wallF3AE4F15-55CE-4E5B-BEE4-BC3C74BBADE3