岩石物理相约束下的砂砾岩岩性粒级精细划分 ——以准噶尔盆地乌尔禾组为例

梁则亮，毛晨飞，肖华，陈国军，高衍武，高明，张啸

1.中国石油新疆油田分公司勘探开发研究院，新疆 乌鲁木齐 836413 2.中国石油集团测井有限公司测井应用研究院，陕西 西安 710077

砂砾岩普遍具有近源、快速堆积的特点，其岩性变化较快，结构成熟度和成分成熟度普遍偏低[1,2]，而且还保留了部分母岩的性质，其砾石成分、粒径大小等因素综合反映在测井曲线上，使得砂砾岩储层普遍具有高密度、低声波时差、高电阻率的特征，导致常规测井资料精细划分砂砾岩岩性时的误差较大，如在交会图版中各岩性分布区间重叠度高，岩性精细划分存在较大困难。

目前砂砾岩岩性判别的方法主要有以下几种：赵宁等[3]、张永健等[4]基于岩性敏感曲线结合模型运算建立岩性识别图版进行岩性划分，该方法受限于重构曲线模型的准确度；袁照威等[5]、林香亮等[6]应用支持向量机、神经网络和决策树等模式识别算法进行岩性划分，该类方法所需样本较多，且模型分析及建立过程无法控制；罗兴平等[7]、张明等[8]基于电成像测井图图像特征提取技术，采用图像特征值进行岩性划分，该方法虽然可以直接反映岩石颗粒形态特征，定性识别岩性，但电成像资料测量成本偏高，难以广泛使用。因此，如何进一步深入挖掘常规测井曲线中包含的丰富岩性信息越来越受到研究人员的重视。

综合前人研究思路，该研究以准噶尔盆地乌尔禾组实际测井资料、取心资料等数据为基础，首次将岩石物理相分析技术与粒度中值曲线相结合，采用主成分分析、聚类分析、Fisher判别分析等数学方法，实现对岩性的初步划分；再在岩石物理相约束下，结合粒度曲线对岩性粒级进行细分，建立了一种能够有效划分砂砾岩岩性粒级的方法。

1 研究区砂砾岩特征

准噶尔盆地乌尔禾组砂砾岩储层粒度分布范围广、非均质性强(见图1)。前人研究表明，不同粒径的砂砾岩体，其物性、电性、含油性均存在较大差异[9]，受粒径变化影响，测井精细评价难以开展，且储层电阻率主要受岩石粒径影响，导致流体性质难以准确识别。该研究通过岩石物理相划分结合粒度中值曲线实现岩性粒级的精细划分，为后期测井精细评价等工作奠定基础。

图1 研究区JL20井储层岩性图

2 岩石物理相划分

岩石物理相是指具有相似的岩石学特征、沉积-成岩作用特征及孔隙类型和结构特征等岩石物理性质的储集层单元，是沉积、成岩、成藏和后期构造等作用的综合效应[10-12]。因此，具有一组特定的测井参数值的岩石物理相所对应的岩性为同一类的概率是较大的。

2.1 主成分分析

首先采用主成分分析法将多条测井曲线转化为少数几个综合的特征向量，使其尽可能多地反映岩性信息，并消除各特征向量之间的相关影响[13，14]。

首先采用零-均质规范化(Z-Score标准化)对测井曲线进行标准化处理，处理后的测井数据均值为0，标准差为1，公式如下：

(1)

进行主成分分析时，提取多少个主成分，应综合考虑各主成分的贡献率、累计贡献率以及特征根的大小，一般取累计贡献率达到85%～95%、特征根大于1的因子。在该研究中，综合考虑累计贡献率及特征根大小后，将提取的主成分数量确定为3个，累积贡献率及特征根大小如表1所示，各主成分的系数矩阵如表2所示。

表1 主成分累计贡献率

表2 主成分系数矩阵

各主成分值为标准化后的测井曲线值与其相应系数的乘积的累加，以主成分1为例，计算函数式为：

主成分1=0.405ZqAPI+0.580ZUsp+

0.767Zρt-0.959ZΔt+

0.766Zρ-0.917Zφnc

(2)

2.2 岩石物理相聚类划分

目前主要的聚类分析方法有2种：系统聚类法和K-均值聚类法。由于K-均值聚类法具有高执行效率、可自行确定聚类数的优点，因此选取K-均值聚类法进行聚类分析，并对岩石物理相的聚类数进行优选[15]。

由于各样本点到聚类中心的总距离减小的快慢在一定程度上可以反映出聚类数的合理性。因此，该次研究采用K-均值聚类法对提取的3个主成分进行聚类分析时，分别使聚类数K=3、4、5、…、10，然后分别计算不同聚类数下，各样本点到聚类中心的总距离，可得到不同聚类数下样本点到聚类中心总距离的变化情况图(见图2)。由图2可知，随着聚类数的增加，样本点到聚类中心总距离的变化率逐渐降低，当聚类数为6时，其变化率接近于1。因此，确定最优岩石物理相的聚类数为6。

图2 样本点到聚类中心总距离随聚类数的变化图

表3为各岩石物理相的测井响应特征参数。岩石物理相2和岩石物理相3的自然伽马平均值相近，分别为54.2117API和54.0739API，但其电阻率、密度、补偿中子孔隙度平均值相差较为明显；岩石物理相4和岩石物理相5的电阻率平均值分别为5.3845Ω·m和6.3098Ω·m，相差较小，但其自然伽马、密度、补偿中子孔隙度平均值相差较为明显；岩石物理相1和岩石物理相2的自然伽马平均值相差较大，分别为71.5851API和54.2117API，但两者的电阻率、声波时差、密度、补偿中子孔隙度平均值差异性较小，测井响应特征区分度较低，如图3所示。由图3可知，岩石物理相1和岩石物理相2除自然伽马外，其余测井曲线特征值分布区间及平均值均较为相近，且岩石物理相1具有高自然伽马特征，因此认为岩石物理相1受高泥质含量影响，导致其他测井曲线响应特征不明显，与岩石物理相2的测井响应特征分布区间发生重叠。

表3 各岩石物理相测井响应特征参数

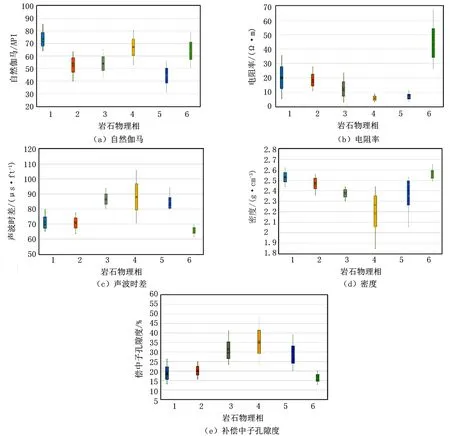
图3 岩石物理相测井响应特征箱形图

2.3 岩石物理相标定

为建立起岩石物理相与岩性之间的对应关系，以准噶尔盆地乌尔禾组的244个岩心样品点的岩性描述为基础，结合粒度分析定名结果，绘制岩性与岩石物理相的直方图(见图4)。由图4分析发现，中砾岩主要以岩石物理相6为主，细砾岩主要以岩石物理相3为主，粗砂岩主要以岩石物理相5为主，中砂岩主要以岩石物理相2为主，泥岩主要以岩石物理相4为主；而细砂岩中所包含的各岩石物理相差别不大，但岩石物理相1相对较多，因此将岩石物理相1代表的主要岩性定为细砂岩。

图4 岩性与岩石物理相的柱状图

由图4可知，各类岩石物理相与岩性并不是严格一一对应的，其中岩石物理相5代表的粗砂岩类别中，粗砂岩实际占比为90%；岩石物理相6代表的中砾岩类别中，中砾岩实际占比为85%；岩石物理相3代表的细砾岩类别中，细砾岩实际占比为83%；岩石物理相4代表的泥岩类别中，泥岩实际占比为81%；而岩石物理相1和岩石物理相2中，其代表的岩性实际占比均远远低于80%。因此，在岩性划分过程中，岩石物理相1和岩石物理相2会使岩性划分的误差增大。因此，该次研究将进一步结合粒度分析数据，建立粒度参数计算模型，在岩石物理相1和岩石物理相2所代表的大类岩性约束下，进一步实现岩性细分。

2.4 岩石物理相判别方程建立

经过聚类分析后，岩石物理相划分类别已经确定，但缺乏明确的判别公式，难以实现对单井储层段的岩性划分。为此，进一步采取Fisher判别分析法建立岩石物理相的判别方程。

图5为Fisher判别分析运算后得到的典则判别函数散点图，可以看到岩石物理相1和岩石物理相2的组质心相近，分布区间重叠度高，与岩石物理相1和岩石物理相2的测井响应分布特征相一致。

图5 Fisher判别分析散点图

运用Fisher判别分析法建立的研究区岩石物理相判别函数计算公式如下：

Fn=anqAPI+bnUsp+cnρt+dnΔt+enρ+fnφnc+gn

(3)

式中：Fn为各岩石物理相的判别函数计算值；n=1、2、…、6，分别对应岩石物理相1、岩石物理相2、…、岩石物理相6；an、bn、cn、dn、en、fn分别为各岩石物理相判别函数中每条曲线对应的系数；gn为各岩石物理相判别函数的常数项。Fisher判别函数系数如表4所示。

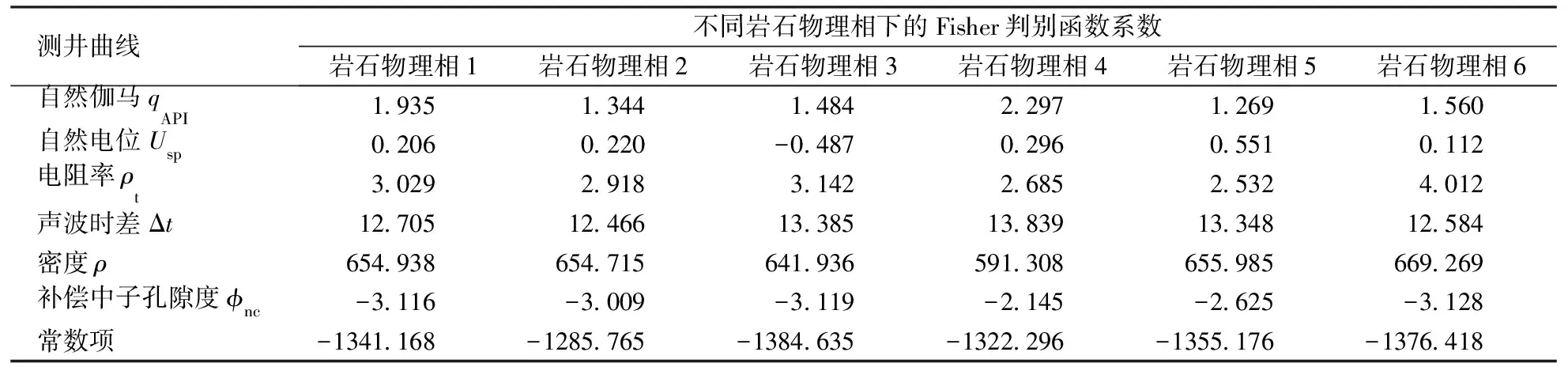
表4 Fisher判别函数系数

对未知岩性进行判别时，把该层段对应的测井曲线数值分别代入各岩石物理相的判别函数中进行计算，根据最大似然原则，计算得到的哪个岩石物理相判别函数得分最高，则该层段就归属于哪个岩石物理相。

为检验该判别模型的准确性，对研究区聚类分析划分出的岩石物理相分类数据进行回判，判别结果如表5所示。

表5 Fisher模型回判结果统计表

总体来看，误判主要出现在岩石物理相1和岩石物理相2的识别中，该结果与测井响应特征分析结果一致，这2类岩石物理相除自然伽马外，其他测井曲线响应特征分布区间相似度较高，导致Fisher判别法识别出现误判。岩石物理相4由于样本数较少，个别样本出现误判时对总体准确率影响较大，导致该类样本识别准确率偏低。

3 粒度参数的计算及模型建立

前人研究认为粒度中值在描述浊流相、河流相等碎屑岩岩性时具有一定代表性[16，17]，为此，研究在岩石物理相1和岩石物理相2代表岩性的约束下，进一步建立粒度中值计算模型，实现岩性的精细划分。

在各类测井曲线中，自然伽马测井曲线值主要受沉积物泥质含量、分选性和粒度变化的影响，因此该条测井曲线被广泛应用于泥质含量的计算中，而“泥质”是一种粒度概念，即自然伽马与粒度之间应有一定的联系。考虑到实际地质状况的复杂性，采用单一自然伽马建立的粒度中值计算模型受到的影响因素较多，可靠性较差。在综合对比分析后，选取自然伽马曲线与电阻率曲线进行多元回归分析，建立粒度中值(采用对数粒级表示，粒度中值=-log2D,D为粒径)与自然伽马、电阻率的关系模型：

计算粒度中值=0.05×qAPI-0.09×ρt-0.706

(4)

为了检验回归公式的模型精度，将研究区4口井取心段粒度分析得到的粒度中值与测井计算得到的粒度中值进行对比分析，结果如图6所示。图6所示数据表明，计算粒度中值与分析粒度中值符合度较高，证明了该粒度中值计算模型的可靠性。

图6 计算粒度中值与分析粒度中值交会图

用上述粒度中值模型对J206井进行计算，效果如图7所示，计算粒度中值与分析粒度中值符合度较高，且曲线变化趋势大体一致，进一步说明粒度中值曲线划分岩性的可靠性。但受限于模型精度产生的计算误差影响和不同岩性粒度中值分布区间难以准确划分的影响，单独采用粒度中值划分岩性的可靠性较低，因此笔者借助粒度中值曲线相对值对岩石物理相1和岩石物理相2的代表岩性进行进一步识别。

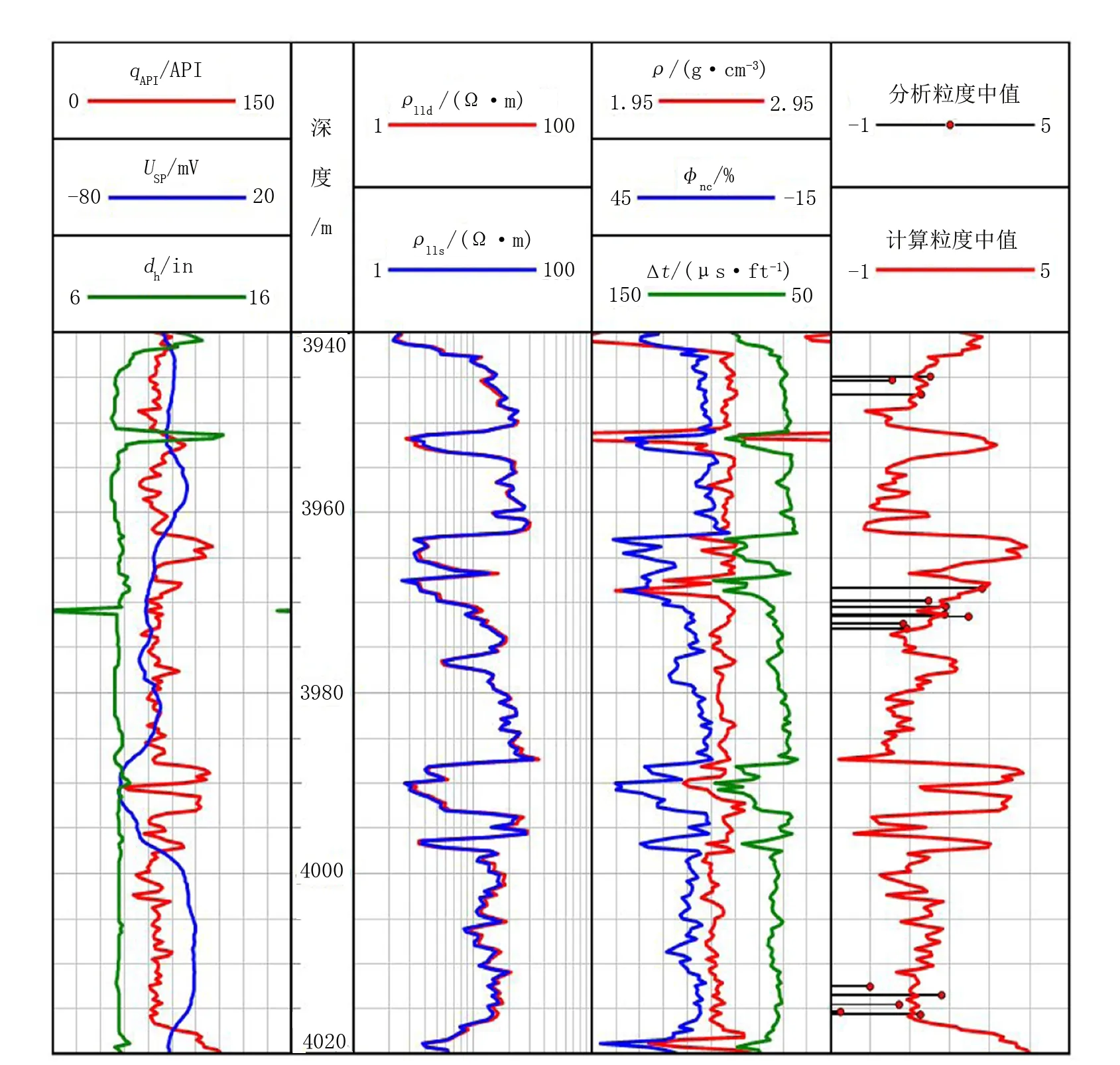
注：dh为井径；ρlld为深侧向电阻率；ρlls为浅侧向电阻率。

4 岩石物理相约束下的岩性粒级划分效果

根据研究区岩石物理相与岩性分类统计结果对比分析发现，岩石物理相1与岩石物理相2中包含的主要岩性分别为细砂岩、中砂岩、粗砂岩、细砾岩，上述4类岩性占岩石物理相1与岩石物理相2样本数的97.5%；再结合岩石物理相1与岩石物理相2的粒度中值曲线变化情况，可将岩性按以下粒度中值变化范围进一步划分：细砂岩，粒度中值≥1.5；中砂岩，1≤粒度中值<1.5；粗砂岩，0.5≤粒度中值<1；细砾岩，粒度中值≤0.5。

图8是该研究区J206井某一层段取心岩性剖面、录井岩性剖面与运用笔者所提出的岩石物理相与粒度中值相结合的岩性粒级划分方法确定的岩性剖面对比图。由图8可知，岩性较粗的粗砂岩、细砾岩、中砾岩段(图8中②、③、④)完全对应，泥岩段(图8中①)基本对应，在中-细砂岩段(图8中⑤、⑥)存在少许差异，岩性划分符合率如表6所示，总体符合率为88.9%，证明运用该方法进行岩性精细划分是可靠的。

表6 研究区J206井岩性划分符合情况统计表

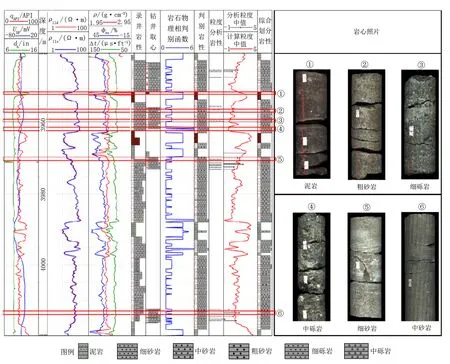
图8 研究区J206井岩性综合划分成果图

5 结论

1)结合聚类分析、Fisher判别分析等方法进行岩石物理相划分后，再根据粒度分析岩性与岩石物理相的统计关系，对岩石物理相进行标定，实现了研究区岩性的识别划分，但岩石物理相1与岩石物理相2标定效果较差。

2)沉积岩粒度中值的变化范围和规律可以反映岩性的粗细与结构。该研究采用自然伽马曲线与电阻率曲线，建立了粒度中值计算模型，结合岩性判别函数，对识别效果较差的岩石物理相1与岩石物理相2的岩性进行了进一步的精确划分。划分结果与岩心描述岩性符合度较高，证实了该方法划分岩性的可靠性。