基于KPCA与IHHO-LSSVM的电力变压器故障诊断方法研究*

宋立业 范抑伶 王燚增

(1. 辽宁工程技术大学电气与控制工程学院 葫芦岛 125105；2. 国网冀北电力有限公司检修分公司 北京 102488)

1 引言①

电力变压器作为维持电网系统安全稳定运行的重要设备，其运行状态会时刻影响着电力系统运行的稳定性与可靠性[1-2]。另外，在当代对电力系统运行可靠性与稳定性的要求逐渐提高的时代背景下，对电力变压器进行实时监控与运行状态分析显得尤为重要。

油浸式变压器因其容量大、节能低噪以及可靠性高等优势在电网系统中得到广泛应用，当其发生故障时，绝缘油中会产生H2、CH4、C2H6等多种气体，其气体含量与故障类型呈现较强的非线性特征相关性。因此，油中溶解气体分析(Dissolved gas analysis, DGA)技术普遍用于变压器故障诊断之中[3]。通过对油中各种气体浓度分析来识别变压器运行状态的传统方法主要有Roger’s法以及IEC三比值法[4]等，这些方法虽然已经被广泛应用，但是普遍存在因判定边界绝对化以及故障数据缺漏而导致的识别准确率低的问题。随着智能算法的不断发展，利用DGA与智能算法相结合对变压器运行状态进行识别的方法已经得到了广泛的关注，目前研究较多的智能诊断方法主要有极限学习机[5-6]、人工神经网络方法[7-9]以及支持向量机(Support vector machine，SVM)方法[10-11]等。文献[12]以DGA气体比值作为输入，采用NSGA2对极限学习机的参数进行优化求解，提高了模型的稳定性和诊断精度；文献[13]通过胶囊网络中卷积层将变压器故障原始数据映射到特征空间，实现关键特征的自动提取，从而进行变压器故障诊断，该模型误判率低，稳定性高；文献[14]通过托梅克链接移除和自适应样本合成的方法对原始数据进行降噪处理及少数类样本数据合成，并将均衡化后的故障数据作为模型输入，结合SVM进行变压器故障诊断，取得了较好的诊断效果。上述方法虽然在变压器故障诊断中均取得了相对不错的效果，但极限学习机存在识别精度易受随机选择的隐藏层权值与偏移值参数的影响；人工神经网络存在系统复杂以及收敛效率低等问题[15]；SVM方法其本质为二分类器，对变压器多分类问题的诊断效果不佳。

最小二乘支持向量机(Least square support vector machine, LSSVM)是SVM的一种扩展，能够将二次规划问题转化为线性方程组求解。相比于SVM，LSSVM降低了计算复杂性，并提升了收敛速度与精度，对多分类问题的处理能力较强，但LSSVM的惩罚因子C和核参数σ对分类结果有非常重要的影响，人工调参需要有专业的知识背景及相关经验，由此，本文先对变压器原始数据进行非线性降维，然后采用哈里斯鹰(Harris hawk optimization，HHO)群体智能优化算法对LSSVM的参数进行寻优，以期获得更高的变压器故障诊断的准确率

针对上述LSSVM参数不易确定的问题，提出基于核主成分分析(Kernel principal component analysis, KPCA)与改进哈里斯鹰算法(Improved Harris hawk algorithm, IHHO)优化最小二乘支持向量机的变压器故障诊断方法。为提高识别效率，首先利用KPCA对原始数据进行预处理，去除冗余数据；其次结合Sigmoid变形函数与点对称策略对哈里斯鹰算法进行改进，平衡算法的全局搜索与局部开发以及跳出局部最优的能力；然后采用经KPCA特征提取后的数据作为模型训练样本集对LSSVM模型进行网络训练，以加快模型收敛，同时采用IHHO算法对LSSVM的惩罚因子以及核函数进行优化求解，从而获取最优诊断识别模型。最后，通过实例分析验证了本文所提方法的有效性。

2 油中溶解气体成分特征的提取

KPCA将变压器原始故障数据映射到高维特征空间，进行主成分分析，得到低维特征[16-17]，从而提取出变压器故障诊断模型输入的主成分。

C为

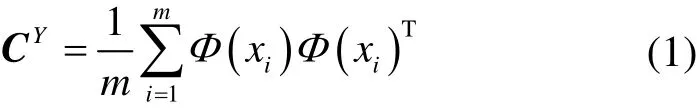
对Y中数据进行主成分分析求解，方程如下

式中，特征向量为v，特征值为λ。特征向量v可由高维空间Y中样本点集Φ(xi)(i= 1,2,… ,m)线性表示为所对应的权值。式(2)两边左乘Φ(xv)(v= 1,2,… ,m)，可以得到

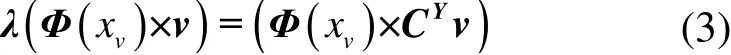
进一步地，把特征向量v代入式(3)，可得到式(4)

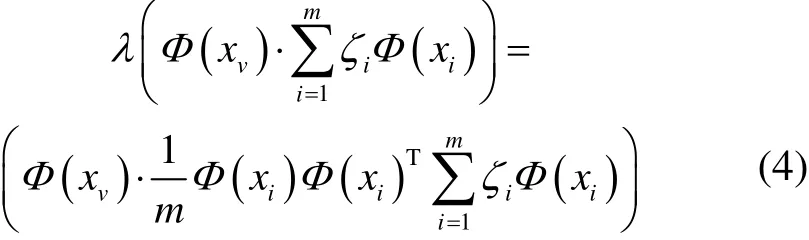
令 矩 阵K= (Φ(xμ) ⋅Φ(xv))，把CY、v代 入式(4)，式(4)可简化为λKζ=K2ζ，则得到CY的特征值和特征向量。则Φ(x)在νk上的投影为

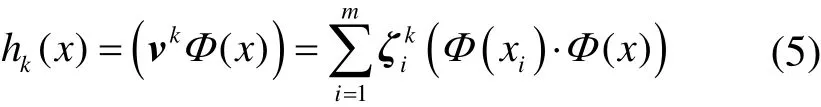
3 LSSVM算法原理

给定变压器故障数据集(xi,yi)x∈Rl,y∈R，i= 1,… ,m，其中xi是变压器故障输入数据，yi为对应的故障类别。LSSVM回归求解最优化问题的目标函数[18-19]如下

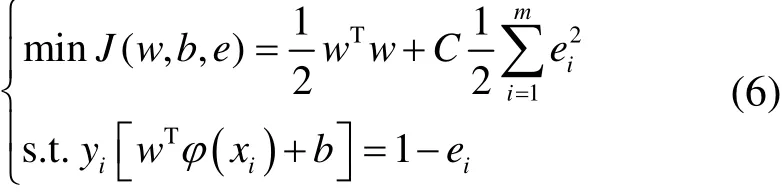
式中，ϕ为xi在特征空间的映射；w为权值向量；b为偏置量；ei为误差变量；C为惩罚因子。

式(6)中对应的拉格朗日函数为

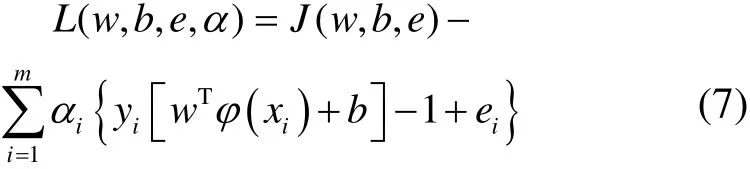
式中，L(w,b,e,α)为解决无约束优化问题的目标函数。对式(7)中的每个变量求偏导，根据Mercer定理[20]，采用径向基核函数(Radial basis function，RBF)

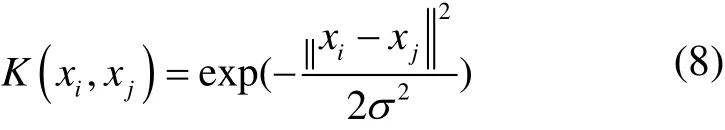
对偏导结果中的ϕ(x)Tϕ(x)进行替换，得到LSSVM的分类函数的表达式如下

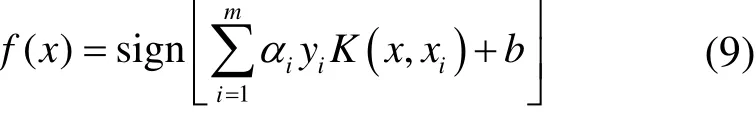
由LSSVM算法建模过程可以看出，LSSVM算法分类精度的高低主要取决于其惩罚因子C和核参数σ，因此，为提高LSSVM算法的分类精度与泛化能力，采用IHHO算法对两个超参数进行智能优化。

4 IHHO-LSSVM算法建模

4.1 HHO算法

HHO算法是2019年仿哈里斯鹰觅食行为而提出的一种仿生智能算法，具有收敛速度快、调节参数少、全局搜索能力较强的优点[21]。该算法主要分为探索阶段和开发阶段，并通过逃跑能量|E|≥1来判断算法是否执行探索行为。HHO算法的建模过程如下。

4.1.1 探索阶段

当|E|≥1时，哈里斯鹰个体之间分别依据相互之间与猎物之间的距离以概率γ进行个体选择性的更新。个体位置更新方式如下

式中，X(t)为哈里斯鹰个体第t次迭代时的位置；Xr(t)、Xbest(t)与Xave(t)分别为随机哈里斯个体位置、当前最优的个体位置以及所有个体平均位置；lb和ub分别表示上下界；ri(i=1, 2, 3, 4)与γ均为服从[0, 1]均匀分布的随机数。

哈里斯鹰探索阶段与开发阶段的转换是由猎物能量因子E控制的。能量因子计算如下所示

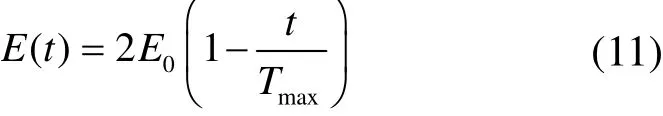
式中，E0为初始能量因子，取值服从(-1, 1)的均匀分布；Tmax为最大迭代次数。

4.1.2 开发阶段

若|E|≥1，算法此时按式(10)执行全局的探索行为；若|E|＜1，则根据不同情况执行局部的开发行为。另外，算法还定义了一个考虑猎物能否逃逸成功的逃逸因子β，并结合|E|与0.5的大小关系，使得算法采取下列4种不同的局部寻优策略。

(1) 软包围。当|E|≥0.5且β≥0.5时，猎物有足够的能量逃逸，哈里斯鹰个体将以软包围的方式进行捕食，个体位置更新公式如下所示

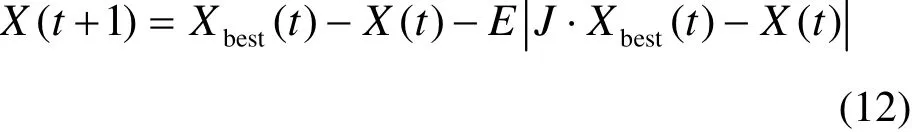
式中，J为猎物逃跑跳跃随机强度，取[0, 2]内的均匀分布随机数。

(2) 硬包围。当|E|<0.5且β≥0.5时，猎物能量较低，哈里斯鹰个体采用硬包围的方式进行位置捕食，公式如下

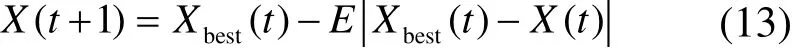
(3) 快速俯冲式软包围。当|E|≥0.5且β<0.5时，猎物有足够的能量逃逸，哈里斯鹰却仍以俯冲的形式对猎物进行软包围，哈里斯鹰个体快速突袭到位置A，如果在位置A处突袭失效，则进行随机游走到位置B，若位置B的适应度值没有提高，则返回原地，个体位置更新公式如下

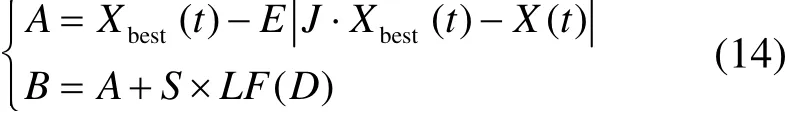
式中，S为D维的随机向量；LF为levy函数。

(4) 快速俯冲式硬包围。当|E|<0.5且β<0.5时，此时猎物逃逸能量不高，哈里斯鹰将以快速俯冲的方式围捕猎物，个体位置更新公式如下

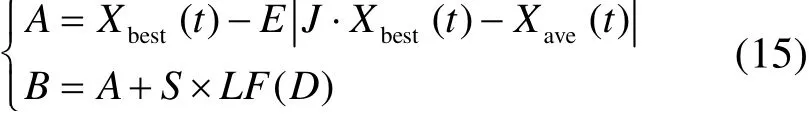
4.2 IHHO算法

4.2.1 非线性逃逸能量更新策略

由HHO算法建模过程可以看出，算法的局部与全局搜索能力是由猎物逃逸能量E决定的，|E|越大表示算法的全局搜索能力越强，反之，则局部搜索能力越强。通过式(11)可知，传统HHO算法中E呈线性递减，表明不能很好地平衡算法的全局与局部搜索能力。针对这个问题，本文提出利用如式(16)所示的Sigmoid变形函数S(x)对HHO算法中的E进行改进以平衡其全局与局部搜索能力。

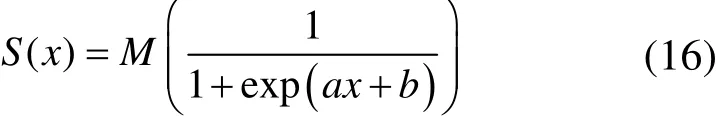
式中，M为幅值大小，a与b分别为伸缩与平移参数。给出幅值为2、伸缩与平移因子分别为0.04与-10时的式(16)所示的函数图像如图1所示。

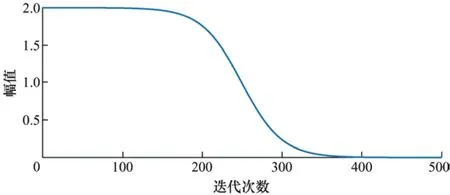
图1 Sigmoid变形函数图像

由图1所示的函数图像可以看出，若猎物逃逸能量E采用此种方式更新，能够保证E在迭代计算前期变化较缓，进行全局搜索；迭代后期E快速下降，利用算法的局部开发，由此，按上述参数改进之后E的更新方式如式(17)所示

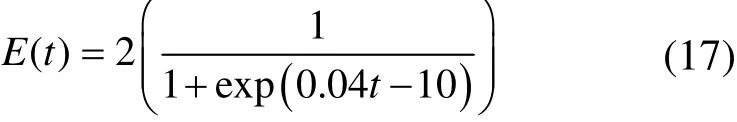
4.2.2 点对称策略

为了提高算法的抗早熟能力，利用点对称[22]的方式在算法迭代计算过程中对算法进行扰动，具体计算方式如式(18)所示

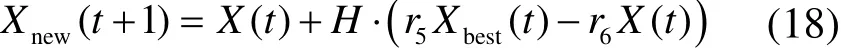
式中，H为对称因子，本文取值为2；r5、r6为0～1的随机数。

由式(18)可以看出，此时算法每产生一个新的位置，立即产生一个围绕当前最优位置对称的扰动位置。算法迭代计算前期，由于个体位置较为分散，产生的扰动较大，随着迭代的进行，由于个体位置较为集中，扰动逐渐减小。由此可见，点对称的扰动方式既可以提高算法的抗早熟能力，又能提高算法的局部搜索能力。

4.3 算法验证

为验证IHHO算法的有效性及优越性，通过与HHO算法以及GA算法进行对比，分别对能检验算法多维计算精度、多维以及低维条件下抑制早熟能力的多维单峰、多峰以及低维多峰优化问题进行求解。式(19)给出的函数求解维数分别为30维、30维与4维，最优解分别为0、0与0.000 3，具体三维图像如图2所示。

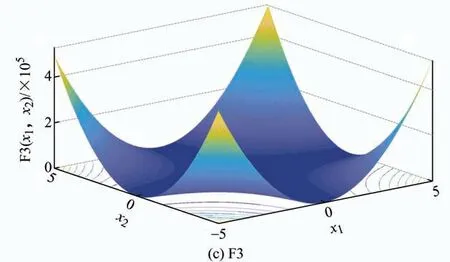
图2 函数图像

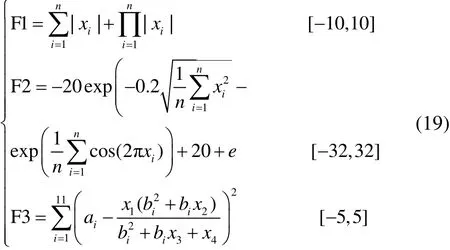
在测试不同算法的寻优性能试验中，经过多次的反复测验，当IHHO算法的伸缩因子、平移因子与对称因子分别为0.04、10、2时，寻优效果最佳，GA算法的交叉与变异率参数分别为0.01与0.5时寻优效果最佳。为保证所有算法的共有参数一致，上述算法种群大小均为50，迭代次数为500。给出三种算法30次计算结果最小值Min、平均值Mean及方差Std如表1所示，迭代过程如图3所示。

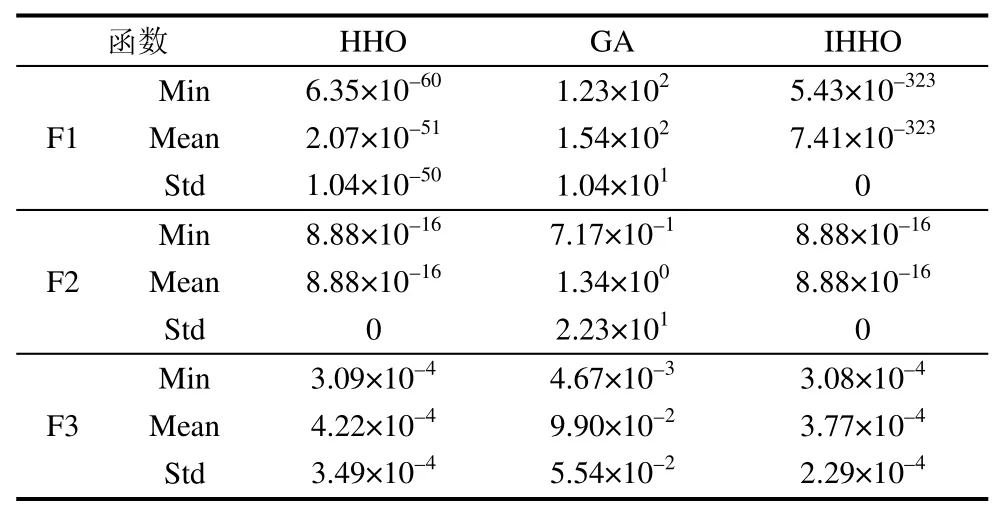
表1 算法计算结果表

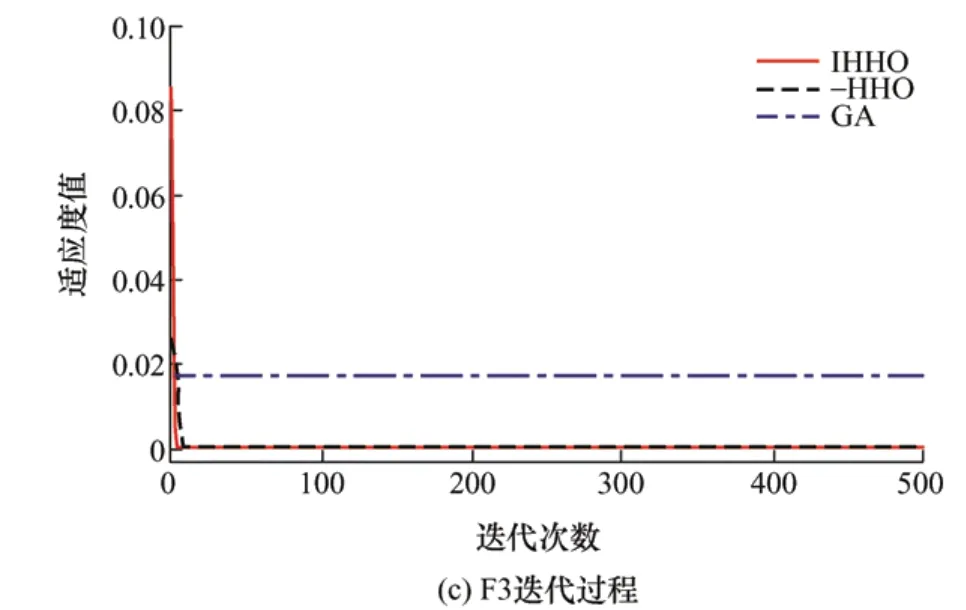
图3 迭代过程图

取测试中与结果平均值相近的一次绘制迭代收敛对比曲线，其中横轴表示迭代次数，纵轴表示适应度值。通过基准测试函数迭代收敛曲线的绘制，进一步直观地对比各个算法的收敛性和算法跳出局部空间的能力。

由表1和图3可知，对于上述三个基准测试函数，HHO算法和GA算法的收敛曲线趋于平缓，存在不同程度的停滞，而IHHO所需的迭代次数最少，说明其收敛速度最快；IHHO在三个测试函数上的收敛精度均值分别为7.41×10−323、8.88×10−16、3.77×10−4，比HHO和GA明显高出多个数量级，表明IHHO的收敛精度最高；IHHO标准差在三个测试函数上均为最低，尤其是在F1和F2函数上，标准差都达到了0，表明其稳定性最强。在F2函数上，尽管IHHO和HHO的最小值、均值及方差一致，但是IHHO迭代132次就达到了收敛状态，而HHO则需要迭代241次。这是由于Sigmoid变形函数的引入平衡了HHO算法的全局搜索与局部开发能力，对称策略能够帮助算法有效脱离停滞, 避免算法陷入局部极值空间。

综上可知，IHHO算法相比于传统HHO算法和GA 算法具有更好的局部极值逃逸能力、整体寻优协同性和收敛性能。

4.4 IHHO-LSSVM算法流程

通过第4.3节及以上的分析，现给出变压器故障诊断的整体流程，具体算法流程图如图4所示。

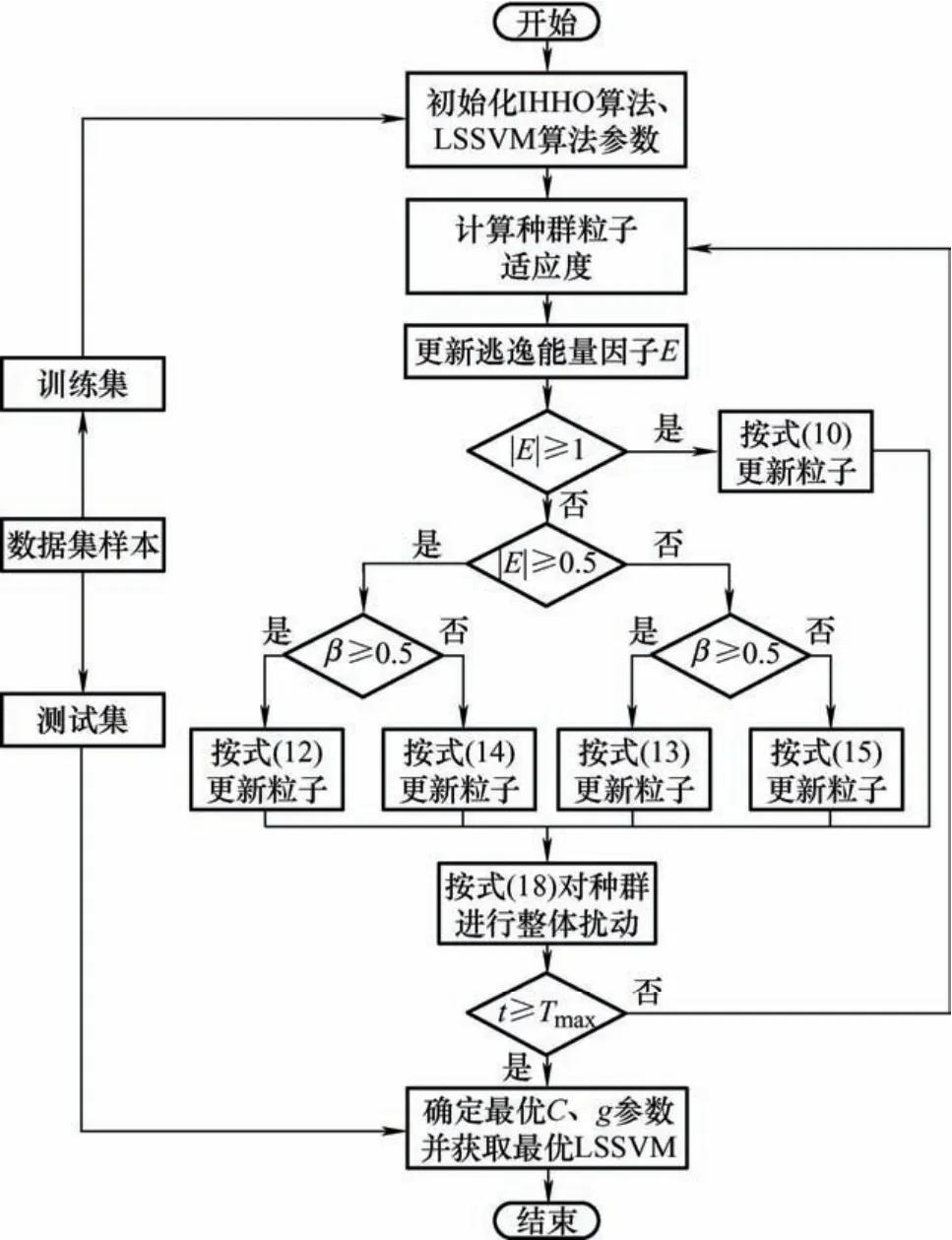
图4 IHHO-LSSVM算法流程图

步骤1：将变压器故障数据进行KPCA降维，然后降维后的数据按照2∶1的比例划分训练集与测试集。

步骤2：设置最大迭代次数Tmax与种群规模N，设置LSSVM惩罚因子C和核参数σ两个参数的取值范围，随机初始化种群。

步骤3：构建IHHO-LSSVM变压器故障诊断模型，将哈里斯鹰个体的适应度值映射为故障判别准确率，即变压器故障模型正确预测的分类个数n与总样本个数m的比值，表达式为Acc=n/N。

步骤4：根据式(17)更新逃逸能量因子E，根据式(18)对种群进行扰动，更新哈里斯鹰个体的位置，并选择当前最优位置。

步骤5：判断当前是否达到最大迭代次数或适应度值最高，若满足条件，则将最优参数的数值赋予LSSVM，否则返回步骤3。

步骤6：根据IHHO优化之后的最优参数构建IHHO-LSSVM变压器故障分类预测模型，输出变压器故障类型。

5 方法试验验证

本文数据由国家电网冀北电力有限公司提供，其中包括变压器正常运行、高温过热、中低温过热、高能放电、低能放电以及局部放电6种运行状态的油样数据共270组，对所提方法有效性以及优越性在Matlab中进行了综合验证。在试验过程中，对采集得到的包括H2、C2H2、C2H4、C2H6、CH4、CO与CO2共7种气体浓度数据，利用KPCA对变压器原始故障数据进行预处理，将预处理过的数据样本集按照2∶1的形式划分为训练集与测试集，同时采用k为5的K折验证法分别对IHHO-LSSVM、GA-LSSVM以及HHO-LSSVM算法进行训练，具体样本分布如表2所示。

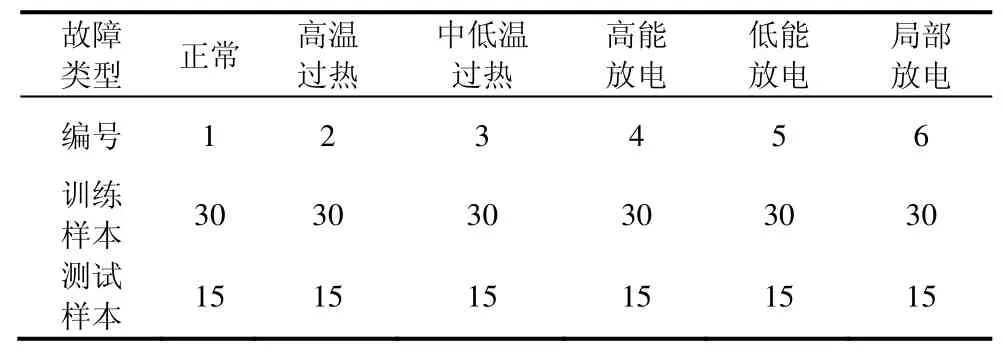
表2 数据集样本分布

5.1 数据预处理

变压器原始故障数据属于非线性数据存在的无效和冗余信息会影响模型收敛速度及诊断精度。因此采用KPCA对故障数据进行非线性降维，从而提高模型的收敛速度及诊断精度。对7种故障特征数据进行核主成分分析，得到Pareto图如图5所示。

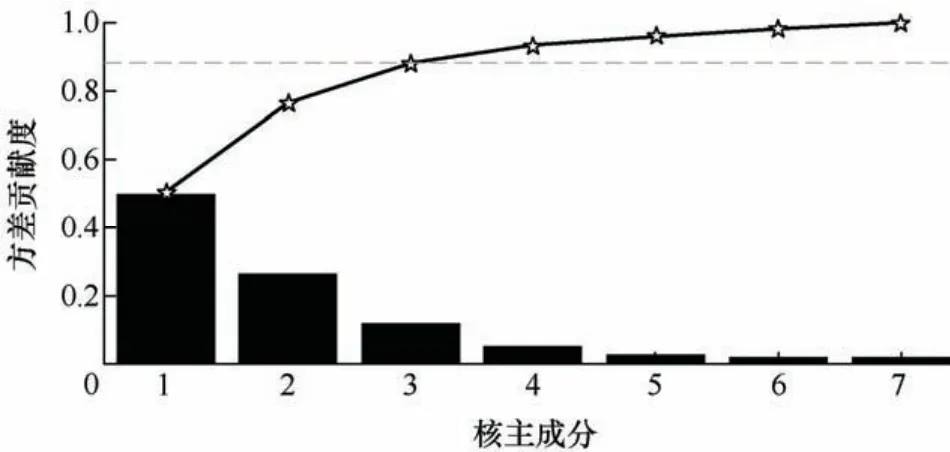
图5 核主成分分析Pareto图

由图5可知，前三个主元的累计方差贡献度为0.880 3，表明这三个主元能够实现所有主元表达能力的85%以上，因此选取前三个主元作为变压器故障诊断模型的输入向量，列举每个主元特征向量中的10个元素，如表3所示。

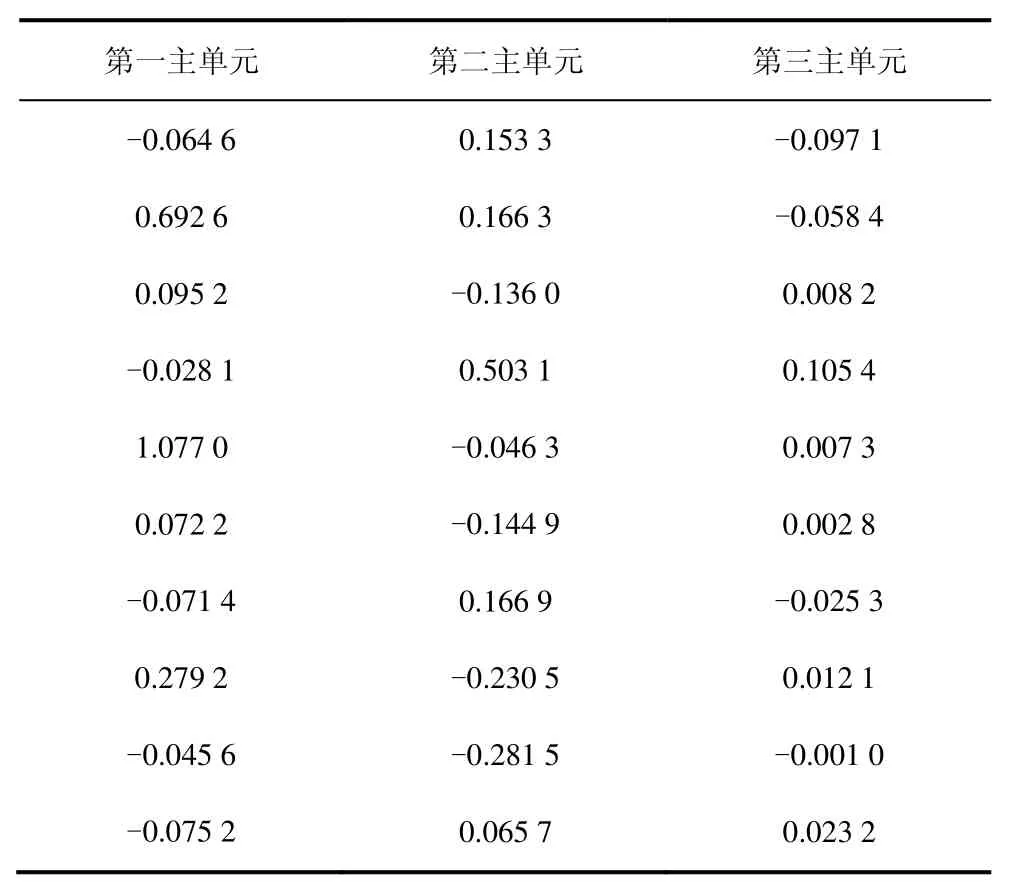
表3 主成分的特征向量

5.2 算法寻优比较

由于LSSVM的惩罚因子与核参数对训练学习效果有着显著的影响，因此采用IHHO对LSSVM的两个超参数进行寻优，并与HHO和GA的优化结果进行对比分析。以KPCA降维后的数据作为模型输入，以诊断精度为适应度值的迭代曲线如图6所示。

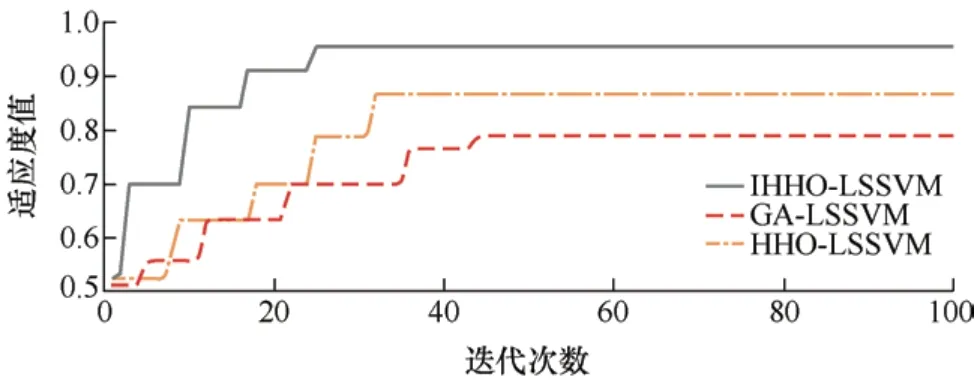
图6 适应度变化曲线

由图6可知，GA算法在对参数的优化中效果不佳，导致适应度较低。标准HHO算法由于全局搜索能力较弱、局部开发能力不强，因此在迭代32次后才达到全局最优解。加入了Sigmoid变形函数与点对称策略的IHHO，仅迭代25次就达到收敛状态且适应度值最高。由此可见，利用IHHO优化LSSVM相关超参数建立变压器故障诊断模型具有可行性。

5.3 诊断结果及其对比分析

为考虑KPCA特征提取前后，特征信息对变压器故障诊断模型精度的影响，以KPCA特征提取前后的特征信息作为变压器故障诊断模型的输入，通过各故障诊断模型得出实际故障诊断类别。KPCA特征提取前的诊断结果如表4、图7所示，KPCA特征提取后的诊断结果如表5、图8所示。

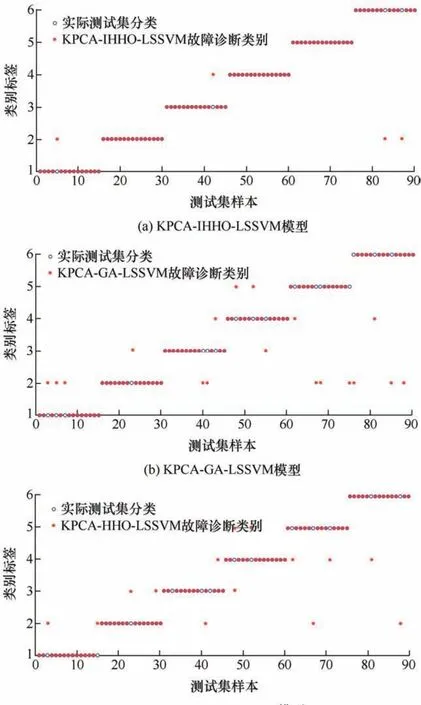
图8 降维后不同模型识别效果

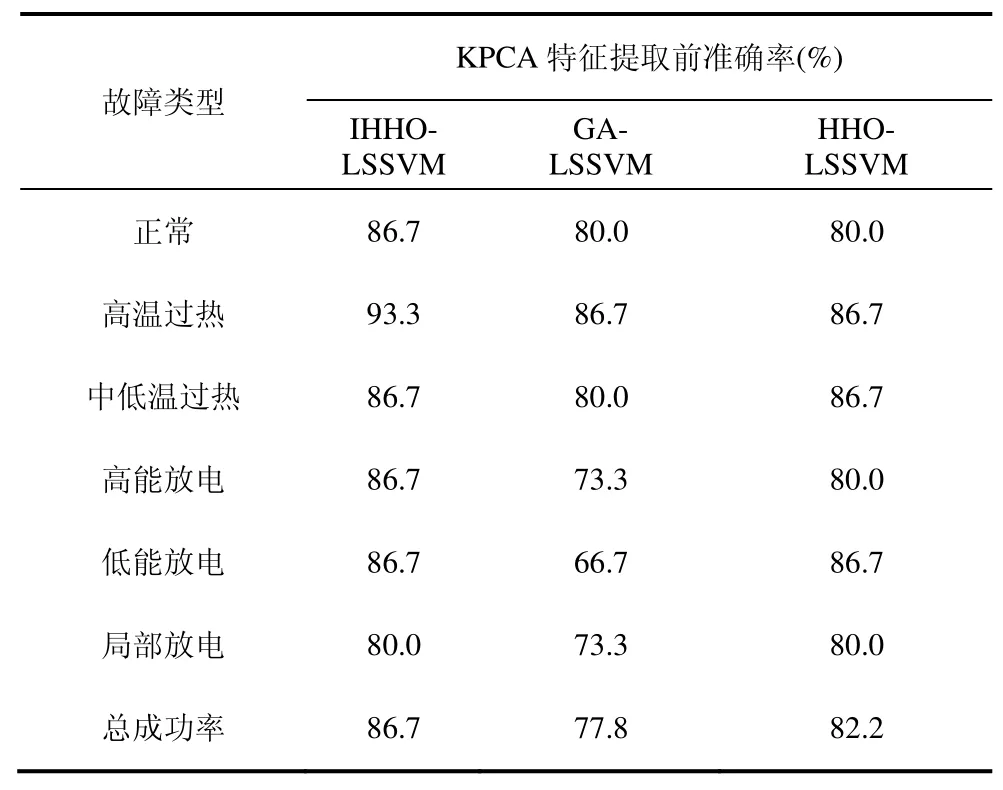
表4 降维前不同故障诊断的正确率

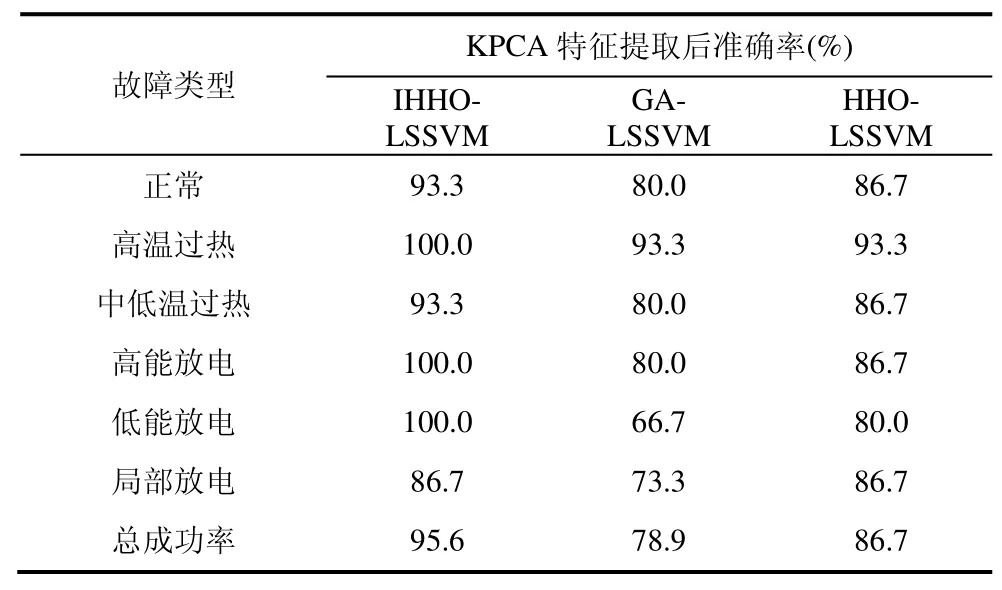
表5 降维后不同故障诊断的正确率

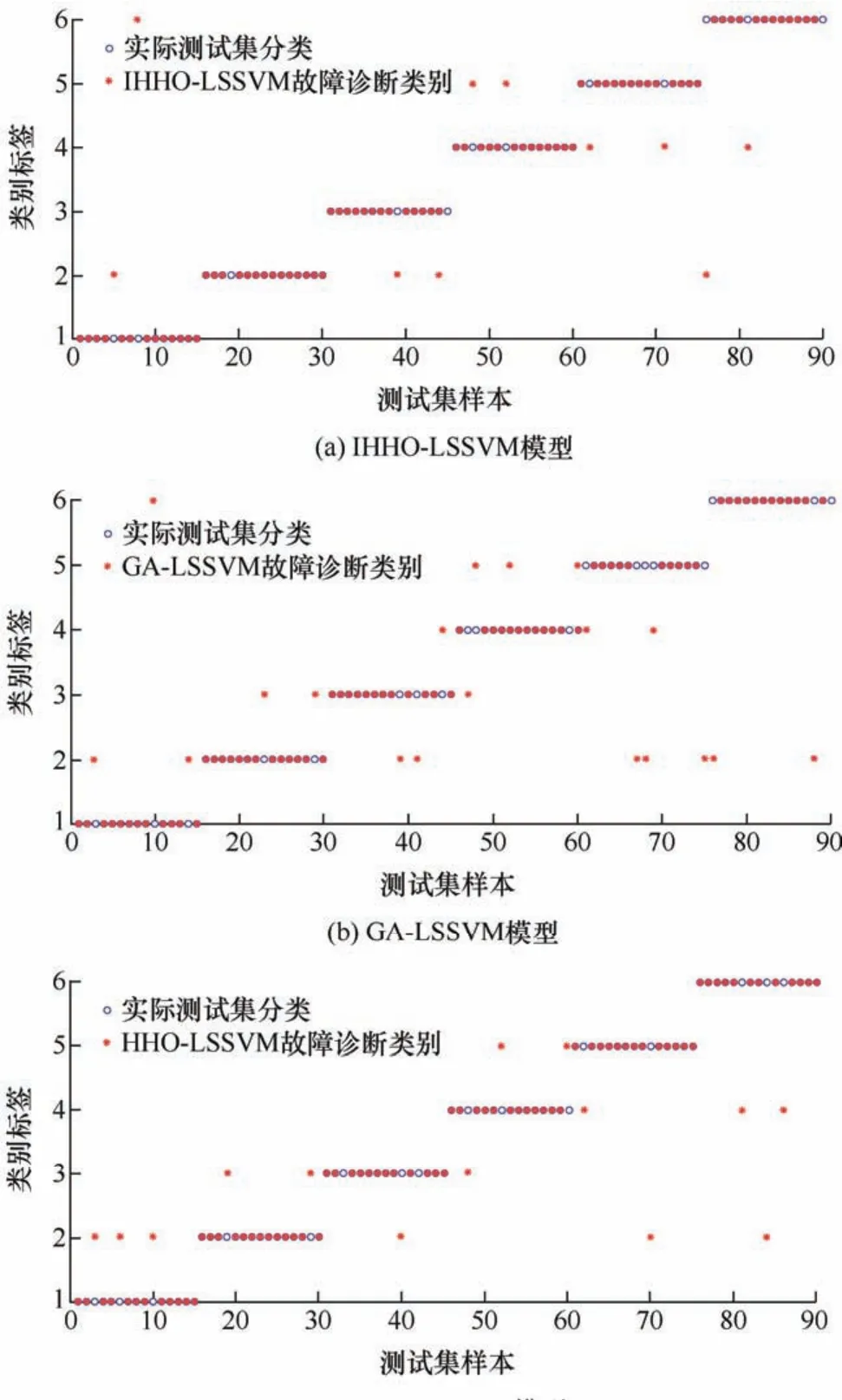
图7 降维前不同模型识别效果

由表4以及图7可以看出，在无KPCA数据预处理的情况下，IHHO-LSSVM、GA-LSSVM以及HHO-LSSVM算法的识别精度分别为86.7%、77.8%以及82.2%，与其他两个变压器故障诊断模型相比诊断精度分别提高了 8.9%与 4.5%，且IHHO-LSSVM故障诊断模型在高温过热故障类型中较为敏感。验证了在没有对数据进行预处理的情况下，文中所提诊断模型仍然具有一定的优势。

结合表5与图8可知，经KPCA数据预处理之后，3种诊断模型的识别效果均得到了不同程度的改善，诊断精度分别为95.6%、78.9%以及86.7%，与其他两个模型对比分别提升了 16.7%、8.9%，且所提模型对高温过热、高能放电以及低能放电故障类型较为敏感，但对局部放电诊断效果不佳。另外，对比KPCA数据预处理前后变压器某个状态的识别效果，可以看出KPCA数据预处理之后的识别精确程度也相应得到了一定的提升，分别提高了8.9%、1.1%以及4.5%。验证了所提文中所提模型在变压器故障诊断中具有较好的可靠性及稳定性。

6 结论

为提高变压器故障诊断精度，本文结合油中溶解气体分析技术提出了基于 KPCA 与IHHO-LSSVM的变压器故障诊断方法。通过结合Sigmoid变形函数与点对称策略对传统哈里斯鹰算法进行改进，平衡算法的全局搜索与局部开发以及跳出局部最优的能力。使用改进后的哈里斯鹰算法对LSSVM的相关参数进行优化选择，进而提高算法的识别精度与泛化能力，并结合核主成分分析(KPCA)对故障特征指标降维，去除了无效和冗余特征加快了模型收敛速度。通过与HHO-LSSVM、GA-LSSVM变压器故障诊断模型相比，文中所提方法能够更准确地对变压器故障信息进行可靠的诊断，验证了所提方法的有效性及优越性，具有一定理论研究和工程应用意义。