考虑换流器伪量测建模的交直流混联电网状态估计方法

李幸芝，韩蓓，李国杰，汪可友，徐晋

（上海交通大学电力传输与功率变换控制教育部重点实验室，上海市 闵行区 200240）

0 引言

随着新能源技术的快速发展，分布式电源（distributed generation,DG）在电力系统的渗透率日益提升。直流网络由于其具有网损低、供电容量高、换流器投资费用低等优点因而有利于DG及直流负荷的接入[1]。DG的不确定性特点也使其需要接入互联大电网以促进多区域间的灵活消纳。因此，考虑多端柔性直流技术的交直流混联电网可以有效接入DG及直流负荷，促进新能源消纳，被认为是未来电网的发展趋势[2]。

为了实现对交直流混联电网的自动化监测和安全控制，需要研究状态估计技术来提供安全可靠有效的实时运行状态数据。目前传统电网自动化系统中配置的量测装置所获取信息种类简单且数量有限[3-4]，大量接入电网的DG和用户负荷通常未配置量测装置，加剧了实时量测的不足；DG出力和用户负荷通常具有不确定性和随机性，这会造成状态估计的不确定性和高误差性；量测装置和本地调度中心存在通信的延迟或干扰使得某些设备由可观测状态转为不可观测状态。这些问题严重抑制了交直流系统灵活调度的发展。因此需要研究更有效的交直流混联电网的状态估计来提高系统的运行可靠性和调度灵活性。

目前针对交直流混联电网状态估计问题，国内外的研究工作主要围绕以下几个方面展开。

1）算法本身的研究。交直流状态估计主要分为统一迭代法[5-8]和解耦迭代法[9-11]。文献[5-7]介绍了基于统一迭代的交直流混联系统估计算法，该算法应用于晶闸管直流输电技术的场景。文献[9-10]介绍了数学变换上的交直流解耦策略，交替迭代计算实现状态估计。文献[8]和文献[11]则以VSC型高压直流输电（high voltage direct current，HVDC）为背景分别提出了交直流状态估计的统一迭代算法和解耦迭代法。

2）直流子系统的建模。在直流状态变量的选择上，文献[6-7,10]认为每个换流站需要采用6个状态变量（Udi、Idi、ki、cosθi、Iai、φi）来描述，其中Udi为换流器i的直流电压；Idi为换流器i的直流电流；ki为换流变压器变比；cosθi为换流器i的触发角（整流）或熄弧角（逆变）；Iai为交流侧注入电流；φi为换流器i的功率因数角。文献[8,11]则在此基础上，通过已知VSC换流器的基础简化到3个状态变量（Udi、Mi、δi）。但考虑直流侧对交流影响时，其量测修改方程形式较为复杂。

3）考虑DG入网的研究。文献[12]提出一种计及多种DG的交流网分布式三相状态估计，考虑了直接入网和经两种换流器控制策略并网的DG功率伪量测数据获取。

以上文献均不考虑换流器本身损耗；其伪量测数据形式不统一，对其拟合数据来源要求更为严苛；负荷及DG的伪量测建模主要采用历史数据，对其不确定性不作额外处理，均以换流器控制信息已知，与本地调度中心通信正常作为前提条件。因此还需要尽可能挖掘电力系统本身的伪量测信息，研究换流器通信接口存在与否时其量测信息的获取技术，增加量测数据冗余度。

提高量测数据冗余度的方法可借鉴于已有电网状态估计思想：①建立三相电网模型，解决三相潮流不平衡问题[12]；②引入相量测量单元（phasor measurement unit,PMU）量测，将其与传统数据采集与监视控制（supervisory control and data acquisition,SCADA）量测有效结合[13]；③利用分布式状态估计减少集中式调度中心通信负担以满足实时要求[12]。其中考虑PMU量测的混合量测数据同步性问题会对状态估计造成影响，可能导致调度中心处理器空闲、实时性较差等问题；分布式状态估计可能存在通信时滞、数据丢包等异常情况下子系统数据不可观测时引起的局部不收敛等问题。这些方法都依赖于通信设备和中央协调器的合作，当通信设备出现不可观测状态时，其状态估计往往受到影响，因此不能解决前文提出的问题，需要研究新的伪量测建模技术应用于交直流混联电网中来应对通信接口出现问题时的情景。

综上所述，本文针对VSC控制信息已知和未知（是否可观测）两种情况，提出基于WLS的改进交直流混联电网状态估计方法。首先采用计及VSC损耗的数学模型，选择VSC的交流侧电压幅值、相角及直流侧电压幅值为状态变量，并以此建立VSC量测方程，简化修改交直流接口量测的方程。针对VSC是否可观的情景，提出两种VSC伪量测建模方法：基于控制信息对可观型VSC进行伪量测建模，基于GMM对不可观型VSC进行伪量测建模，提高状态估计量测数据冗余度；在原有交流状态估计算法的基础上提出了一种改进的交直流混联电网状态估计，并充分利用原有交流程序，完整计入交直流系统耦合性。最后，采用经过修改的IEEE-14节点系统从含可观型VSC伪量测时算法对不同量测配置的鲁棒性、含不可观型VSC时算法对不确定性描述的有效性以及抗差性三个方面进行三种案例的仿真计算，验证算法的有效性和实用性。

1 交直流系统模型及量测方程

1.1 交直流系统模型

交直流混联系统模型如图1所示，交流子系统通过VSC与直流子系统相连接。假设交流子系统共有Nac个交流节点，直流子系统共有Ndc个直流节点，VSC个数为NVSC。由此可将交直流系统划分为以上三部分。图1中U、δ分别为交流子系统节点电压幅值、相角；Uc、δc分别为VSC的交流侧电压幅值、相角；Ud为直流子系统节点电压幅值。本文状态估计的目的即求取这些状态变量的值。

其中，以VSC控制信息是否上传到本地调度中心为分类原则，将已知控制信息的VSC称为可观型VSC，未知控制信息的VSC称为不可观型VSC。

由图1可知，VSC作为连接交直流系统的重要控制器件，应采取精确合理的建模。本文采取了计及损耗的VSC模型，如图2所示。

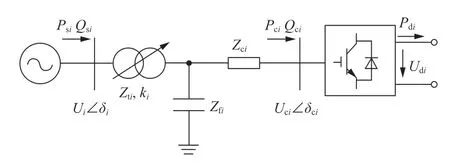
图2 VSC等效电路Fig.2 The equivalent circuit of the VSC converter

交直流系统稳态运行时，交流子系统经换流变压器Zti、滤波器Zfi和换相电抗器Zci与VSC母线连接。VSC直流侧采用双极接线连接到直流母线，采用Y-Δ变换可消去滤波器支路节点得到交流电网注入换流站有功功率Psi、无功功率Qsi及注入VSC母线处有功功率Pci、无功功率Qci如下[14]：

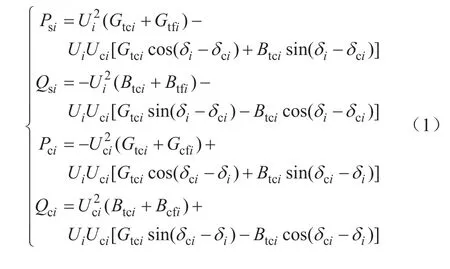
1.2 交流子系统的量测方程

交流系统的量测量主要采用传统的节点电压幅值量测Ui、节点注入有功功率量测Pi、节点注入无功功率量测Qi、交流支路潮流有功功率Pij、交流支路潮流无功功率Qij。

对Nac-NVSC个不与VSC相连的交流子系统内部节点有以下量测方程：

式中：下标j是直接和下标i相连的节点；θij为节点i和节点j间的相角差；Yij=Gij+jBijYij为节点i和节点j间的导纳；Ysi=Gsi+jBsiYsi为节点i的对地导纳。

对NVSC个接有VSC的交流子系统边界节点需要修正交流侧注入功率量测方程为：

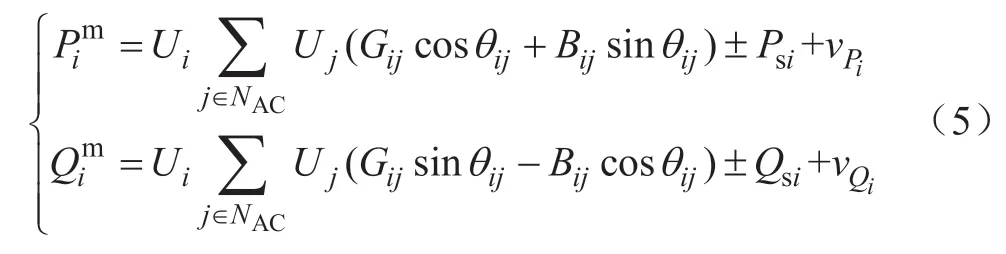
式中：Psi、Qsi当交流系统向直流系统注入功率时取负号。

式（4）—（5）中：vUi、vPi、vQi、vPij、vQil分别代表第i个交流节点的节点电压幅值量测Ui，节点注入有功功率量测Pi、节点注入无功功率量测Qi、交流支路潮流有功功率Pij、交流支路潮流无功功率Qij的量测误差。

1.3 直流子系统的量测方程

对Ndc-NVSC个直流子系统内部节点，可得到如下量测方程：

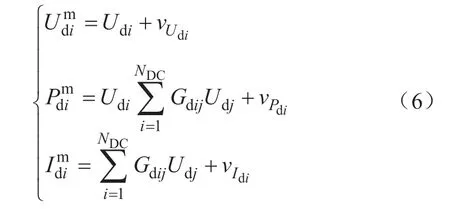
对NVSC个与VSC相连接的直流子系统边界节点，可得到如下量测方程：

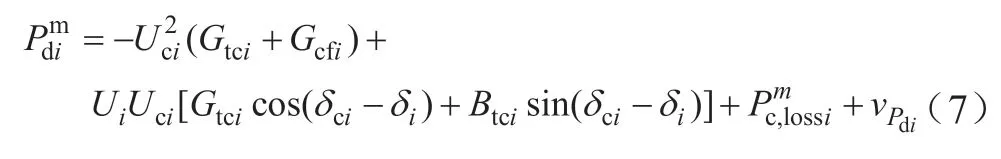
式（6）—（7）中：vUdi、vPdi、vIdi分别代表直流子系统第i个节点的电压幅值量测Udi，注入直流功率量测Pdi、注入电流Idi的量测误差。

2 VSC伪量测建模

随着DG、储能系统、微电网、电动汽车等在电网中的渗透率的提高，电力系统面临的随机性和波动性也日益增加。通常，本地调度中心需要与各个VSC换流站进行通信以获取其运行模式和控制信息。因此，可观型VSC带来的已知控制信息可以作为伪量测数据来提高状态估计的精确度。当通信出现干扰或无法通信时，VSC由可观型转为不可观型；同时对于未配置量测信息的DG等设备，其VSC的运行模式与相应控制信息也难以实时获取。因此本文将分别讨论两种VSC伪量测建模方法：可观型VSC采用VSC的控制特性方程统一伪量测形式，将控制信息纳入伪量测数据；不可观型VSC通过GMM方法提取历史负荷或者出力预测数据的不确定性信息来得到精度较高的伪量测数据。

2.1 基于控制信息的VSC伪量测建模

接受集中控制的VSC或控制信息（控制量测及目标）可及时传达至调度主站的VSC被称为可观型VSC，这类VSC主要考虑基于已知控制信息及其方程进行伪量测建模。由于VSC采用全控型开关器件，每个换流器可以同时控制直流侧某一状态变量（直流电压、直流功率或直流电流）和交流侧某一状态变量（交流侧电压或交流侧无功功率），因而有4种控制方式。由于VSC控制的目标值接近于实际运行值，可认为由此添加的伪量测值较为精确，并且能反映当前时间断面或一段时间内的系统运行状况，因而可给定较高权值σ。

本文考虑4种VSC控制策略，随系统的控制目标和控制方式不同，可增添相应的伪量测方程。

1）定PS、定QS。

此时伪量测数据可直接选择为：

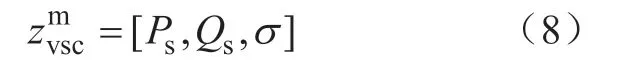
2）定PS、定Ui。

基于VSC量测方程（1），已知第i个VSC交流母线侧电压Ui，可联立式（2）和式（3）求出Pci，进一步联立Pci、Psi可解得Uci、δi-δci，进一步求出Qsi，因而伪量测数据与式（8）相同。

3）定Ud、定Qs。

VSC换流器需满足电压约束

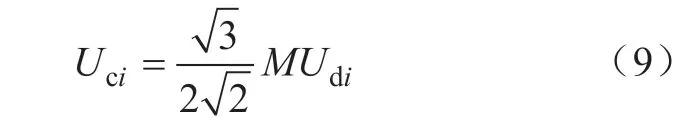
式中：M为VSC的调制比。由式（9）可得Uci，再由式（1）可联立Pci、Uci、Qsi得到Ui和δi-δci，进一步求出Psi，因而伪量测数据与式（8）相同。

4）定Ud、定Ui。

由式（1）可知，已知第i个VSC交流母线侧电压Ui，可联立Pci、Uci解得δi-δci，进一步求出Psi、Qsi，其伪量测数据形式与式（8）相同。

上述分析表明采用VSC控制特性方程可将以不同控制方式运行的可观VSC伪量测建模用统一形式表达如式（10）所示，从而简化伪量测方程形式。

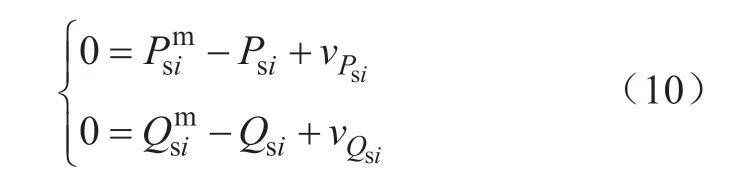
式中：vPsi、vQsi分别代表Psi、Qsi的量测误差。

2.2 基于GMM的VSC伪量测建模

当系统进行状态估计时，若对不可观型VSC控制信息暂时无法获取，则不能同可观型VSC一样根据控制方式写出具体伪量测方程。

仿照VSC伪量测方程（10），本文采用与VSC相连的可估计交流子系统或直流子系统的负荷或出力值作为伪量测数据。通过历史数据或出力预测等信息进行估计拟合时，其精度较低，因而在功率数据的基础上添加功率的标准差σ作为伪量测数据：

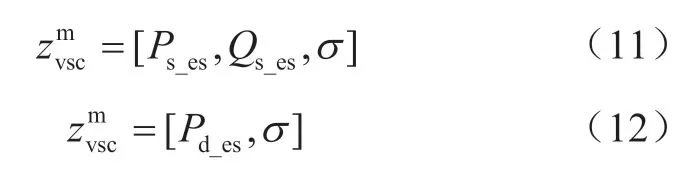
式中：Ps_es、Qs_es为与VSC连接的交流子系统的负荷或出力的估计值；Pd_es为与VSC连接的直流子系统的负荷或出力的估计值；σ为对应负荷或出力值的标准差。

其相应添加到交流子系统或直流子系统的伪量测方程为：

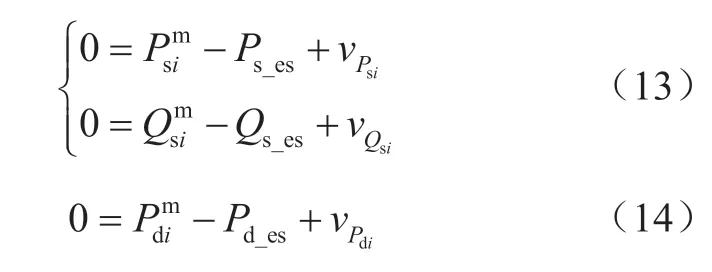
通过VSC入网的负荷或电源形式多种多样，本文以DG为例进行讨论。DG可以通过VSC接入交流子系统，也可以通过VSC接入直流子系统。为了提高不可观型VSC的伪量测数据的精确度，应计入DG出力的不确定性。近年来，已有不少学者对DG的不确定性进行了合理研究。文献[15]在大量历史数据统计的基础上，建立了DG出力和负荷功率的概率密度函数来描述其不确定性。文献[16]采用区间数理论来对DG的不确定性进行分析和定量描述。

本文采用GMM将一个分布非高斯的出力曲线等效为一个高斯分布函数从而求取其均值和标准差[17]。在GMM里，DG的出力预测概率密度函数可被等效为几个不同的正态分布函数：

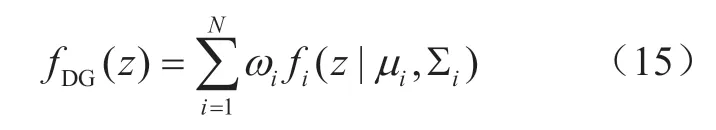
式中：N为子高斯函数的个数；µi、∑i分别是第i个子高斯函数的均值和方差；ωi为第i个子高斯函数的权重值。

这些子高斯函数满足：

等效的DG出力高斯函数的均值和方差求解为：

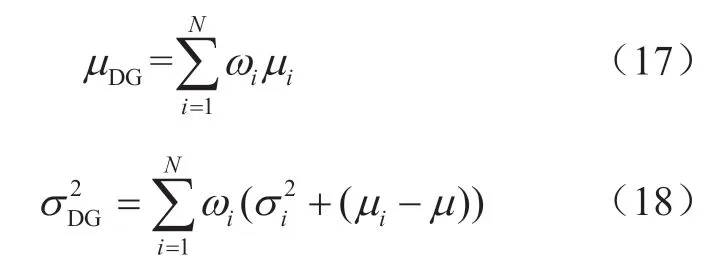
由此可得一个如图3所示的具有高斯分布的等效DG功率概率密度函数，其均值和标准差即可作为式（12）—（13）的伪量测数据。因此，利用GMM描述DG的不确定性即将对应DG出力的均值作为Ps_es,Qs_es,Pd_es代入相应伪量测方程，并将σDG作为σ替换下文交直流混联状态估计中对应位置上原有的量测权重值进行求解，以此将伪量测中含有的不确定性纳入状态估计的计算中。

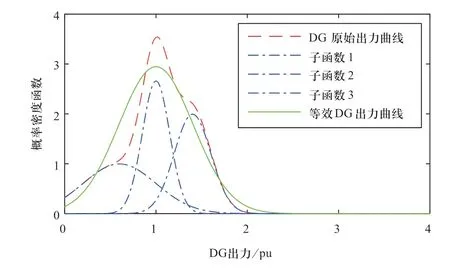
图3 GMM原理示意Fig.3 Description of GMM theory

3 交直流状态估计方法实现

结合前文所述，由于VSC伪量测数据已转化为交流侧量测数据，故列写入交流量测数据，将待估计交直流混联系统待求状态变量和量测方程列写为：

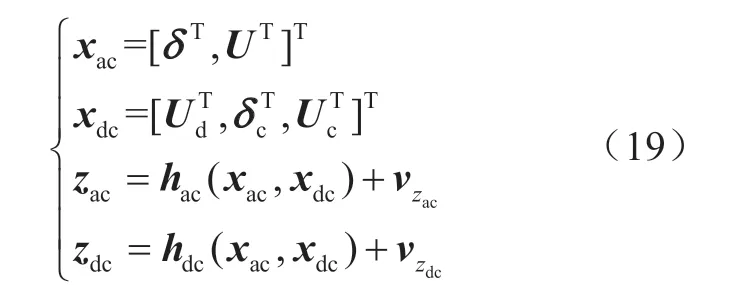
由于电力系统非线性加权最小二乘状态估计算法中量测方程具有冗余度，故量测方程个数大于状态量个数，因此构造如下目标函数使量测误差方差加权求和最小：

各状态变量的迭代计算公式为：

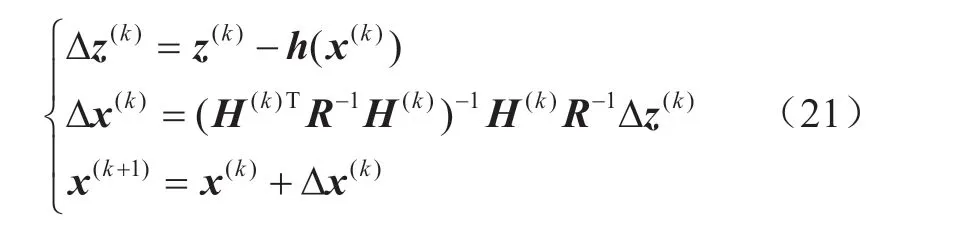
式中：上标k表示第k次迭代；Rac、Rdc分别表示各交流量测和直流量测权重系数的对角阵。

其中量测方程的雅可比矩阵H可写为：

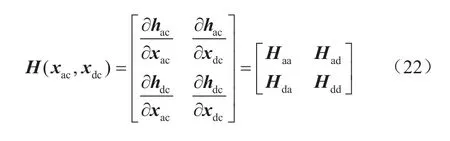
由于直流网络的各状态变量不会出现在交流网络的各量测方程中，故可知：

由此简化，记为：

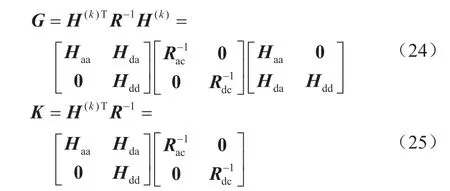
将式（24）、（25）代入迭代公式可得：

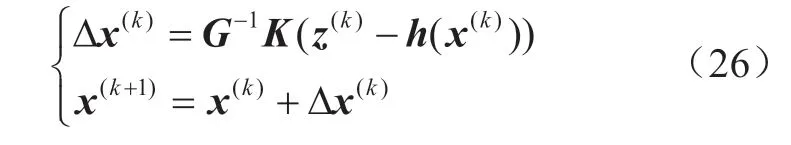
4 算例仿真

本文在IEEE-14节点的基础上构造交直流混联系统，将节点4和节点5之间的交流线路更换为两端含VSC的直流线路，增加直流节点15、16。同时在节点15处接入一个光伏电源，在节点2、节点14处分别接入一个风电电源和一个光伏电源。认为与直流线路连接的VSC可观，与DG相连接的VSC不可观。系统结构如图4所示。其中VSC及直流线路参数如表1和表2所示。DG出力不确定性参数根据历史数据、天气情况所得出力预测曲线经高斯混合模型分解出的子高斯函数参数[17]得到，即此时认为出力预测与系统真实运行间误差为0（误差情况将在算例3中进行讨论），并叠加正态分布的随机量测误差，参数如表3和表4所示。其中风电功率因数为0.9，光伏功率因数为1。各数值均为标幺值。

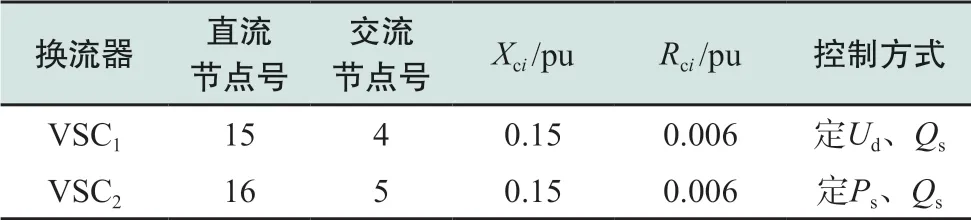
表1 VSC换流器参数Table 1 Parameters of VSC converter

表2 直流线路参数Table 2 Parameters of DC line

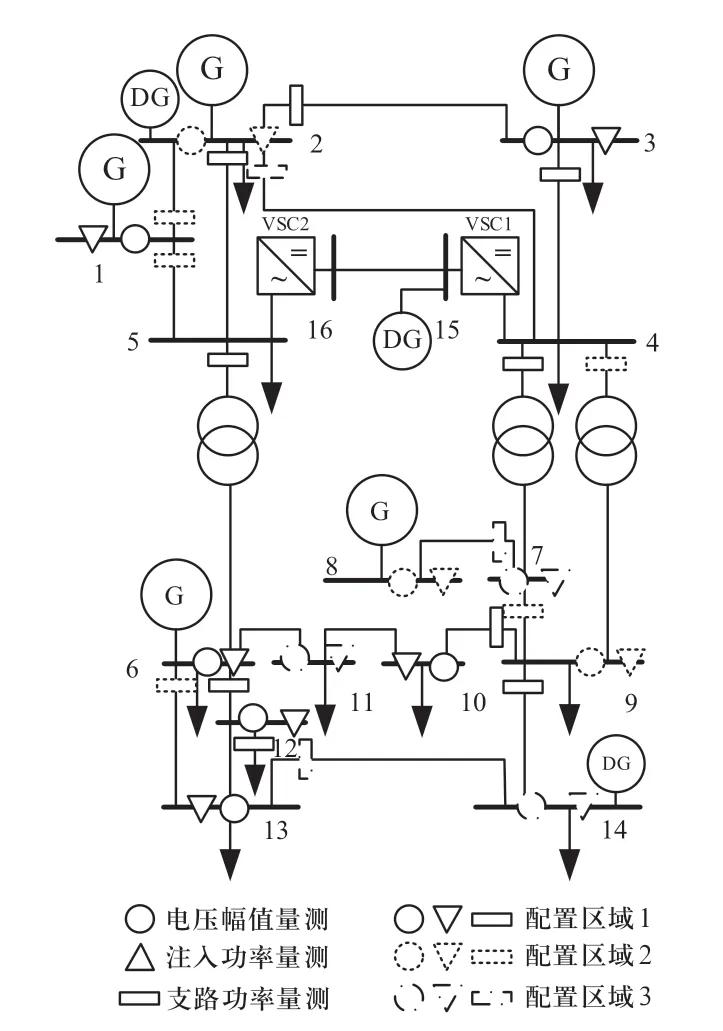
图4 本文研究的交直流混联系统Fig.4 AC/DC hybrid network in this paper

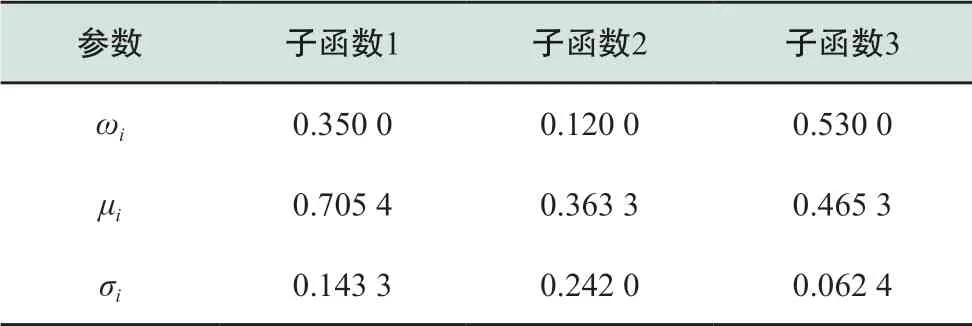
表3 风电GMM参数表Table 3 Parameters of wind power generation using GMM theory

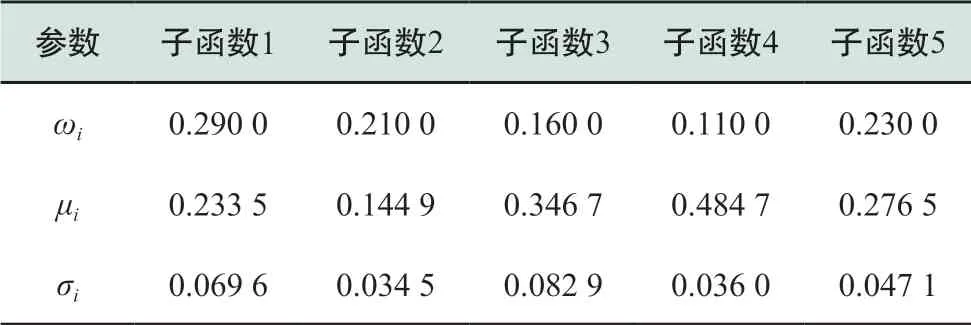
表4 光伏GMM参数表Table 4 Parameters of photovoltaic power generation using GMM theory

量测装置的误差标准差设置如表5所示。

表5 量测误差标准差参数Table 5 Parameters of measurement error standard deviation

为了说明对可观型和不可观型VSC伪量测建模的有效性，本文将通过以下3个算例进行讨论分析。

4.1 算例1：含可观型VSC伪量测的状态估计对不同量测配置的鲁棒性

为直观验证本文对可观型VSC的伪量测建模的有效性，本算例去掉接有不可观型VSC的DG，并使用两种方法建模。方法1：对可观型VSC不作伪量测建模处理；方法2：对可观型VSC作伪量测建模处理。

该系统潮流真值来自交直流混合系统统一迭代法的潮流计算结果，量测装置布点设置如表6所示。

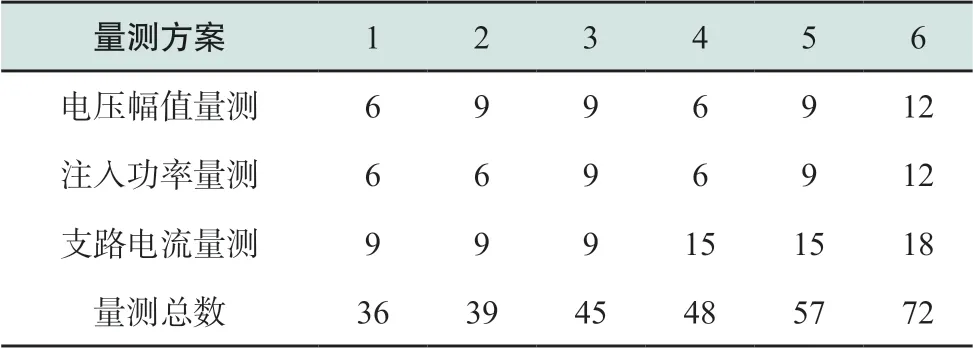
表6 量测装置布点情况Table 6 Parameters of measurement arrangements

量测方案1具体配置如图4中的配置区域1所示，方案2在方案1的基础上追加配置区域2电压幅值量测，方案3在方案2的基础上追加配置区域2注入功率量测，方案4和方案5分别在方案1和方案3的基础上追加配置区域2支路功率量测，方案6在方案5的基础上追加配置区域3所有量测。其中每套量测配置均考虑节点7有功和无功零注入、节点8有功零注入功率约束。

本文采用绝对误差的平均值和最大值作为状态估计的性能指标，性能指标的计算公式为[13]：

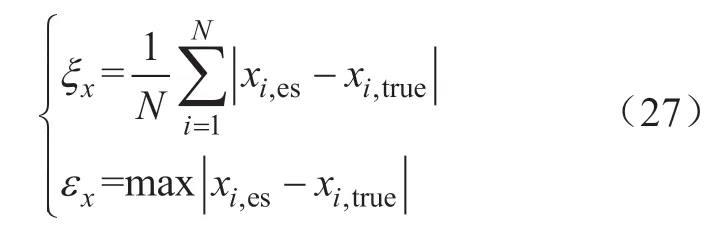
式中：N为系统节点数；xi,es和xi,true分别为节点i状态变量x的状态估计值和真值。

在不同的量测配置方案下进行仿真，交流子系统的状态变量绝对误差如图5所示，其中红色代表方法1，蓝色代表方法2。

不同配置方案下对交流子系统的性能指标和收敛性评价如表7所示。

由图5和表7可以发现：

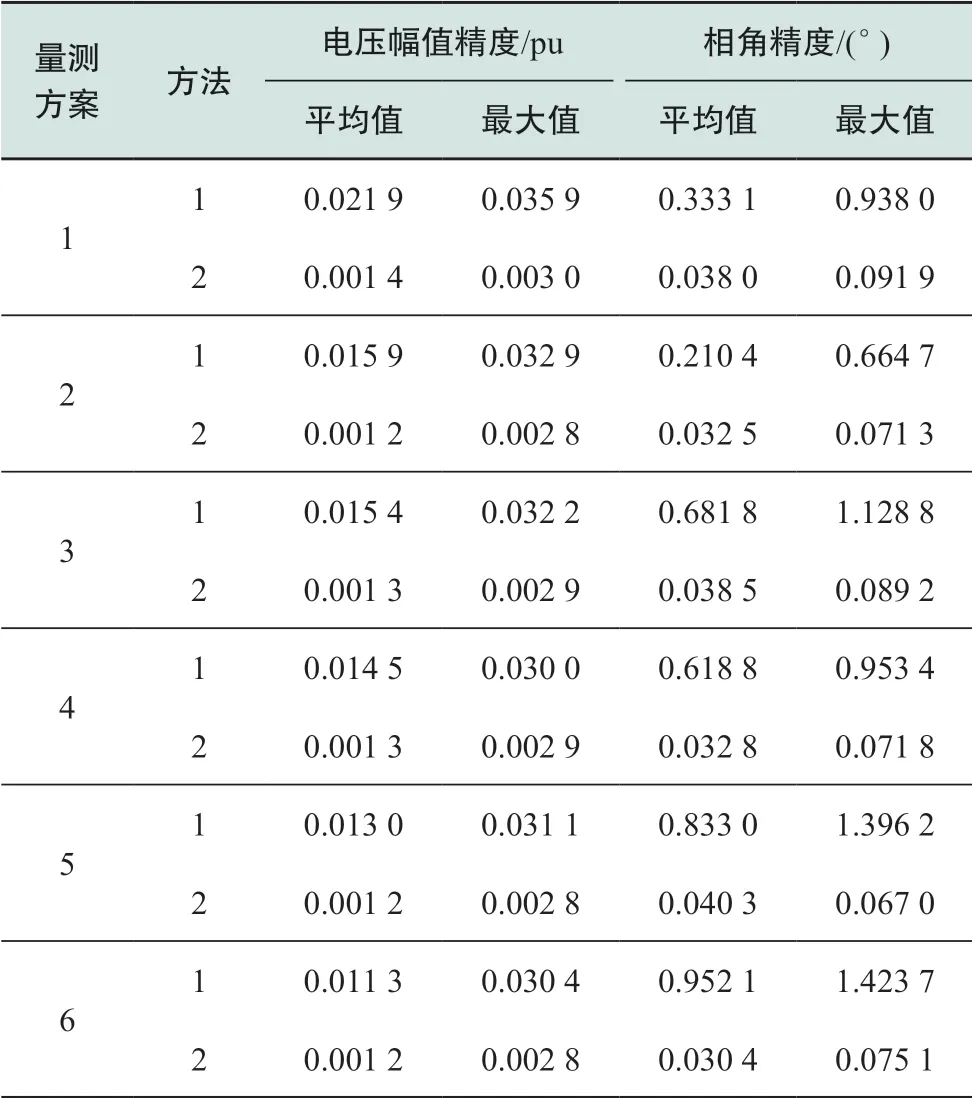
表7 方法1和方法2的状态估计性能指标Table 7 Performance metrics of AC system state variables of method 1 and method 2

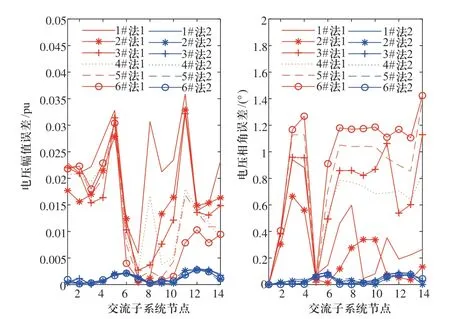
图5 不同量测方案中两种方法绝对误差Fig.5 Absolute error of two methods in different measurement arrangements

1）在量测装置布点位置不发生改变时，方法2的估计误差比方法1更小，即结果更为精确。

2）从量测配置方案1至方案6，方法2的电压幅值估计误差变化最大值不超过2×10-4，相角误差变化最大值不超过8×10-3，而方法1的电压幅值误差变化最大值超过1×10-2，相角误差变化最大值超过6×10-1，即方法2相较方法1对量测配置的依赖性更低。

其中在节点3、8、11依次添加量测装置时，由图5可得方法1的电压幅值精度有所提高，电压相角精度却随之下降。这说明在VSC存在不可观情况下，在相应节点配置电压幅值量测可以直观提高相应节点电压幅值估计结果精度，但其叠加的量测随机误差却会对电压相角的计算造成较大影响。与之对应的方法2在节点3、8、11处电压幅值和电压相角精度均保持稳定。这说明对可观型VSC进行的伪量测建模能更能抓住系统关键信息，用最少的量测配置实现较好精度，体现出对不同量测配置均具有鲁棒性。

上述分析说明可观型VSC的伪量测建模能有效地将当前时间断面上的系统运行信息有效纳入状态估计中，无需采用增加量测冗余度的方式提高精度，对量测配置依赖更小。因此为了经济性和实用性，需要充分利用可观型VSC的控制信息，对其进行伪量测建模，同时也应该对不可观型VSC进行处理来获取更多有用信息。

4.2 算例2：含不可观型VSC伪量测的状态估计对不确定性模型的的有效性

可观型VSC当前的控制信息能反映该时间断面上的潮流信息，能较好跟随系统不确定性的变化趋势。因此在不可观型VSC的伪量测建模应同样满足对不确定性的描述能力。本文在算例1的基础上增加不可观型VSC的情景如下。

情景1：DG总数为3。即图4所示系统，交流节点2接入风电，直流节点15和交流节点14接入光伏。

情景2：DG总数为6。在情景1的基础上，在交流节点3接入风电，交流节点8和12接入光伏。

情景3：DG总数为9。在情景2的基础上，在直流节点16接入风电，交流节点7和11接入光伏。

采用量测配置方案1，潮流真值来自考虑DG波动下的交直流混合系统统一迭代法的潮流计算结果。

为排除可观型VSC对算法影响，考虑以下方法。

方法3：对可观型VSC作伪量测建模处理，对不可观VSC不作处理。

方法4：对可观型VSC和不可观型VSC均作伪量测建模处理。

采用方法3和方法4进行仿真计算，交流子系统各状态变量估计误差如下。

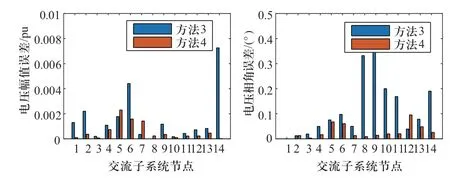
图7 情景2中两种方法估计结果的绝对误差Fig.7 Absolute error of two methods in case 2

由图6—图8可知：

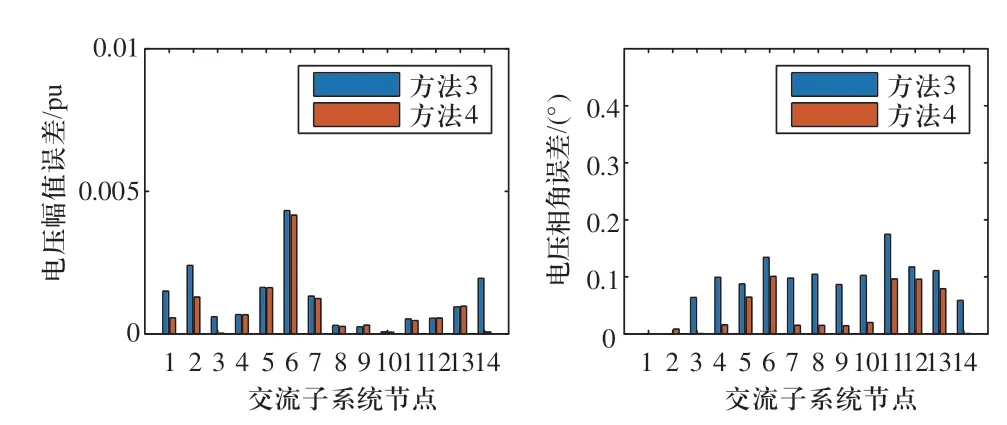
图6 情景1中两种方法估计结果的绝对误差Fig.6 Absolute error of two methods in case 1

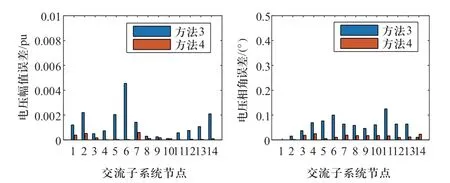
图8 情景3中两种方法估计结果的绝对误差Fig.8 Absolute error of two methods in case 3

1）情景1—情景3中方法4的电压幅值和相角估计误差均小于方法3。

2）随着DG个数的增加，方法4的各节点状态估计误差有逐渐降低的趋势，而对不可观型VSC不作伪量测建模处理的方法3则无法跟随DG波动性的变化，估计结果误差呈现出较大的不确定性。

其中情景1里由于对与节点2、节点14相连的VSC进行不可观伪量测建模处理，方法4相较方法3在节点2、节点14处的电压幅值和电压相角精度明显提升；情景2中节点12处方法4的电压相角误差大于方法3，这是由于量测误差的随机性造成的，状态估计中交流子系统状态变量包含电压幅值和相角，虽然方法4相角误差大于方法3，电压幅值误差却小于方法3，情景3中节点14处情况类似。在整体范围内方法4的电压幅值和相角误差均较方法3有明显降低。

进一步考察情景1中各方法在不同时间断面上的状态估计有效性，引入EKF算法[18]进行动态状态估计并采用均方误差（mean squared error,MSE）来进行各算法的性能对比：

设定1 min内，EKF法分别采样2、3、4、5、6次，方法3和方法4均只采样1次。

由于交流节点2、节点14，直流节点15接入DG，节点6处配备量测装置，故图9给出了1 min内EKF法对节点2、4、6、14电压幅值的状态估计过程。其中节点2在潮流计算中认为是PV节点，电压幅值恒定。图10给出了3种方法在第6次采样时的估计误差对比。表8给出了3种方法的均方误差。

图9 EKF状态估计过程Fig.9 Process of EKF state estimation

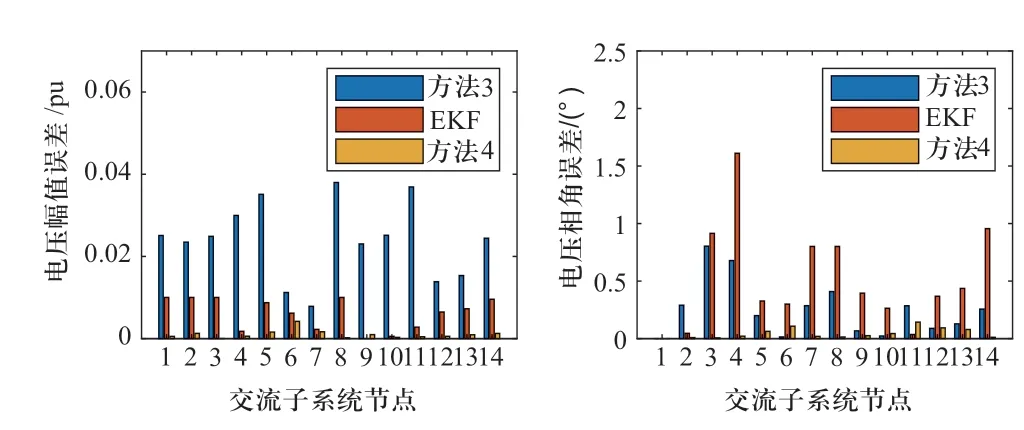
图10 第6次采样时3种方法估计结果的绝对误差Fig.10 Absolute error of three methods for AC system at 6th sampling

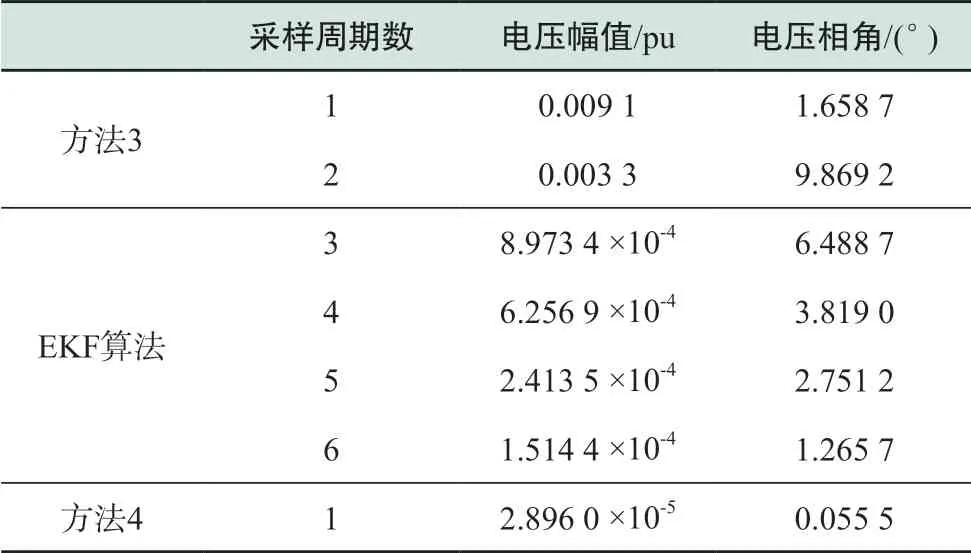
表8 不同采样周期下各算法均方误差Table 8 Mean squared error of three methods under different sampling modes

由图10可得在电压幅值和相角误差方面，方法4均小于方法3和EKF算法。其中EKF算法在部分节点上电压相角上估计误差较大，其原因可能为EKF算法所使用的多次采样数据中DG出力不确定性具有一定程度叠加，而本算例所采用潮流真值为第6次采样时的潮流数据，方法3和方法4均使用1次采样数据，所叠加不确定度较小。

由表8可得，在均方误差指标上，2次采样EKF算法电压幅值精度高于方法3，电压相角精度低于方法3，随着采样周期数的增加，其电压幅值和相角精度逐渐升高，6次采样后电压幅值和相角精度均高于方法3，但仍低于方法4，且具有数量级上的明显差别。

这说明不可观型VSC的伪量测建模能提取一段时间内DG出力的不确定性信息，使得方法4的估计精度相当甚至优于6次采样EKF的精度，能计入一定动态变化的趋势，为少实时量测情形下应用提供可能。

4.3 算例3：不可观型VSC伪量测建模的抗差性

不可观型VSC所采用的伪量测数据是基于历史数据、天气情况等因素预测得到的，精度较低。因此在算例2情景1的基础上进一步讨论当历史数据或出力预测存在误差的情况下的状态估计结果。讨论分析以下4种情形：各DG真实出力情况与其历史数据偏差为1%、5%、10%、40%。仿真计算上，选取DG历史出力数据计算得到潮流真值，在历史出力数据上叠加偏差1%、5%、10%、40%得到DG出力特性曲线从而获取不同偏差下的不可观型VSC的伪量测数据，并选取量测配置1获取量测信息。

采用方法3和方法4进行状态估计，其仿真结果各节点状态变量绝对误差如图11所示。不同情形下性能指标如表9所示。

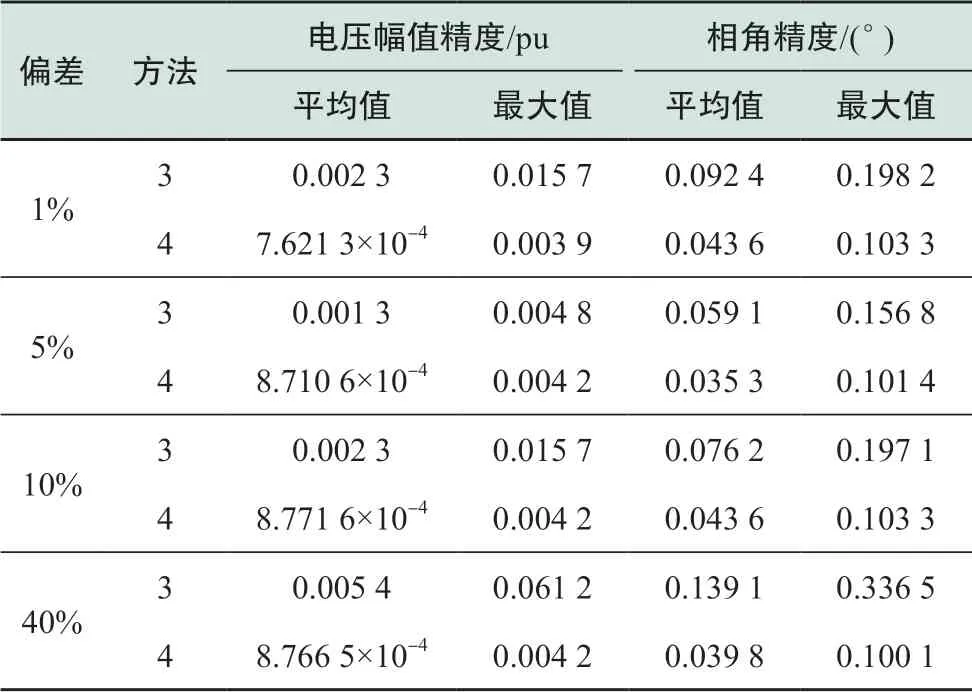
表9 不同误差下两种方法的性能指标Table 9 Performance metrics of AC system state variables of method 3 and method 4

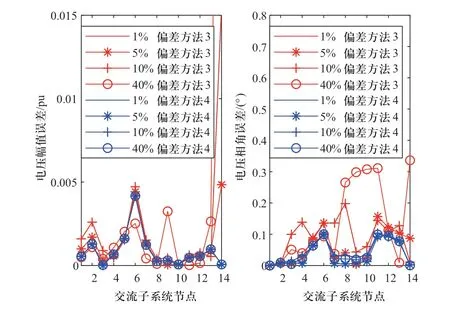
图11 不同情形下两种方法绝对误差Fig.11 Absolute error of two methods in different situations

由图11可以看出：

1）方法3虽未计入DG历史数据，但其估计误差会随着DG本身出力的不确定性有所波动，方法4由于采用了GMM将DG出力的不确定性以标准差形式考虑进状态估计中，可有效容纳叠加在出力曲线上的偏差。

2）随着DG历史出力数据偏差为1%～40%，方法4的误差能保持在一个小范围中，其中在电压幅值方面平均误差变化保持在10-4级别，电压相角方面则保持在10-3级别，具有抗差性。

3）方法4在承受伪量测数据来源有一定误差的情况下，与方法3的波动性相比较，其各情形下误差最大值均小于方法3，即仍能保持一定的精度，说明其鲁棒性更好。

其中从图11可得方法4在节点7、8、9、10处的电压相角绝对误差随着DG历史数据偏差从1%到40%有所增加，但从表9可知方法4电压相角平均误差在各情形下仍维持在4×10-2附近，说明其总体精度变化不大，整体呈现较高精度。

5 结论

本文针对VSC控制信息是否已知将VSC分为可观型和不可观型，对可观型VSC和不可观型VSC分别采用基于控制信息和基于GMM的伪量测建模方法，提出了基于换流器伪量测建模的交直流混联电网的状态估计算法，主要有以下创新点。

1）采用了考虑损耗的VSC模型，提出了新的VSC量测方程，简化了交流接口的修正方程，完整计入交直流耦合，提出一种收敛性较好的交直流混联系统状态估计算法。

2）给出了两种VSC伪量测建模方法：基于控制信息的统一的伪量测方程形式和基于GMM计入一定时间动态变化趋势的伪量测方程形式，提高了伪量测数据精度。

算例仿真充分说明本文所提算法在较低的量测配置下具有较高精度，对量测配置具有鲁棒性；能较好地计及DG出力的不确定性，动态描述能力优于6次采样EKF算法，可运行在实时量测数较少的情况下，采样周期时间可相应增加，可适用于新能源渗透率不断提高的未来交直流系统；能有效利用不可观型VSC信息增加伪量测数据，提高系统经济性和灵活性；在一定程度上允许负荷或DG出力预测与实际运行状况存在误差，具有良好的抗差性。未来研究可以在此基础之上进一步考虑更多类型的复杂电力电子器件的建模，考虑更多电力电子控制策略从而完善估计模型，将算法扩展到电力电子化电力系统状态估计中，为新型电网可靠运行提供技术支撑。