剖析几何概型问题的常见易错点

■姜典术

在一次试验中,古典概型中等可能事件只有有限个,几何概型中等可能事件有无限个。几何概型的概率公式中的“测度”只与大小有关,而与形状和位置无关。在解这类问题时,稍有疏忽就会出错,下面列举两种常见的易错点,供同学们学习与参考。

一、几何度量计算出错

例1 在0～1 之间随机选择两个数,这两个数对应的点把0～1 之间的线段分成了三条,试求这三条线段能构成三角形的概率。

错解:设事件A为“三条线段能构成三角形”,设三条线段的长度分别为x,y,1-x-y。

剖析:错解把长度型几何度量当成计算概率的几何度量。其实,对三条线段的长度加以分析,对应围成的几何图形的面积才是满足条件的几何度量。

正解:设事件A为“三条线段能构成三角形”,设其中两段的长度分别为x,y,则第三段的长度为1-x-y。

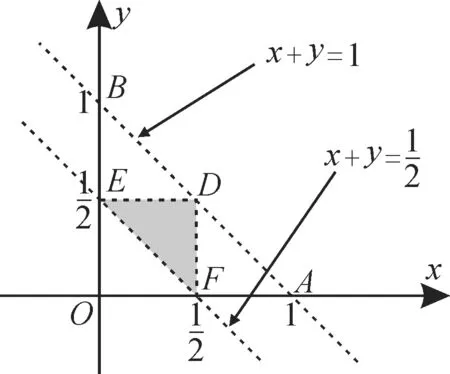
图1

二、几何度量选择出错

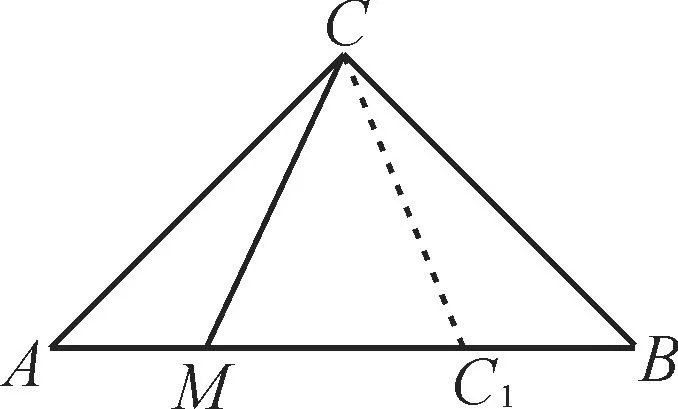
例2 在等腰直角三角形ABC中,直角顶点为C,在∠ACB的内部任作一条射线CM,与线段AB交于点M,求线段AM

错解:在线段AB上取AC1=AC(如图2)。

图2

剖析:上述解法不满足几何概型的等可能性。在线段AC1上任取一点M是等可能的,但不满足在∠ACB内任作一条射线CM是等可能的,因此不能把等可能取点看作等可能作射线。

正解:在∠ACB内作射线CM是均匀分布的,所以射线CM所在任何位置都是等可能的。