机织物中液态水传输的数值模拟

胡倩倩 刘让同 李 亮 刘淑萍 李淑静

（中原工学院，河南郑州，451191）

人类作为恒温生命体通过出汗来降温和散热，而服装作为人体的第二皮肤，具有良好的吸湿快干能力非常重要，特别是当穿着者大量出汗或被雨水等外部液体完全浸湿时，即使是最好的水分管理织物也会被浸湿乃至饱和，变得不可吸收、沉重和黏人，显著降低穿着者的舒适度［1］。影响服装湿舒适性的因素包括透水性、吸湿性、透气性和快干性等，其中，吸湿快干性能是影响织物湿舒适性的一个重要方面［2］。因此提高织物的吸湿快干性能显得尤为重要，国内外很多学者对此进行了研究。在研究方法上数值模拟研究越来越热，通过建模和物理场数值模拟研究织物水传输的学者也越来越多，AGRAWAL Prashant 等人对织物上滴渍的形成进行了试验和数值研究，并用达西定律通过渗吸试验测量机织物的渗吸特性［3］；ALI M A 等人通过非破坏性试验获得三维正交织物在不同压实度下的X 射线显微计算机断层扫描图像来生成3D 模型，使用流体动力学控制方程数值模拟求解边界值［4］；LUO Xiaonan 等人建立了三维几何模型，根据质量守恒、能量守恒、毛细现象推导了新模型，使用时域有限差分法求解偏微分方程，描述织物中热湿传递的物理机制［5］；PALAKURTHI Nikhil Kumar 等人基于有限体积方法，对润湿液体通过虚拟纤维介质的毛细渗透进行微尺度模拟［6］；SHIH Shihhao 等人建立的模型考虑了汗液在多孔介质中的运动、传热、纤维吸收和蒸发，通过CFD 软件包ANSYS Fluent 对其进行求解，模拟人体与织物-环境耦合系统中热湿传递 瞬 态行为［7］；POORUN Yashna 等人推导了一个具有随机项的多相多组分流动模型，用于研究纤维多孔介质中的热湿传递［8］；BARAUSKAS Rimantas 等人提出了一个多层织物与人体之间水汽交换的结构模型［9］；WU Xionghua 等人利用BP神经网络，针对水刺非织造布建立了预测模型进行计算机模拟［10］；WANG Z 等人通过使用多孔纺织品模型对热湿耦合传递的数学模型进行分析［11］；ZHENG Yi 等人基于纱线的微观结构建立三层模型处理液体与纱线之间的相互作用，用于湿吸和芯吸计算［12］。总之国内外研究者对织物液态水传输的研究，要么从试验中采集数据［13-15］，要么利用理论方程间接推理［16-18］，无法直观得到液体在织物中的传输距离，无法系统解释织物液态水传输特性。为此，本研究以机织物为载体，通过研究液态水在不同浮长机织物的铺展传输，分析液态水在机织物中的传输规律，寻找液态水在机织物中传输的最有利结构，探索液态水在机织物中传输的可控性，为吸湿快干服装面料的研究设计提供理论依据。

1 试验

1.1 仿真试验

为了便于验证，选用纱线捻度较大、细度相对较粗、织物密度相对较低的斜纹织物进行模拟。利用建模软件构建不同浮长机织物模型，仿真模拟液态水在其表面的铺展状态和传输行为。网格划分采用有限元软件内置的自由四面体网格和三角网格。三角网格最小单元为0.109 μm，最大单元为0.606 μm，最大单元增长率为1.5，曲率因子为0.6，模型纱线交错等边界狭窄区域分辨率为0.5 dpi，剩余自由四面体网格控制实体迭代次数为4，处理最大单元深度（个数）也为4。网格划分结果如图1 所示。

图1 网格划分

液态水在织物上会受到自身重力、纤维或纱线间毛细作用力、纤维黏附力的作用，三者的合力决定液态水的主传输方向。假设织物水平放置，如果合力以自身重力占主导，液态水主要沿厚度方向传输；如果合力以纱线间毛细作用力占主导，液态水主要沿织物中纱线的浮长方向传输，或沿垂直浮长方向（另一系统纱线的浮长方向）传输；黏附力的存在影响液态水传输的距离。为便于分析，规定正面浮长方向对应y轴，垂直浮长方向对应x轴，厚度方向对应z轴。液态水在织物中的传输既有毛细作用也有扩散作用，毛细作用是织物中纱线间、纤维间的作用力，扩散作用是液态水分子热运动运输现象，是分子通过布朗运动从高浓度向低浓度区域运输的过程。为了准确分析液态水在织物中的铺展传输行为，本研究采用稀物质扩散模型和菲克定律进行数值模拟，分析液态水在机织物上沿x、y和z向的液态水传输过程。

在机织物模型中添加物理场，对物质浓度和机织物属性进行设置，扩散系数0.16×10-12m2/s，水的初始浓度0.055 6 mol/m3，初始含水饱和度0.5，相对分子质量18，动力黏度2.98×10-3Pa·s，机织物体积质量998.2 g/m³，纱线排列密度44 根/10 cm。

1.2 实际测试

选用丙纶长丝进行合股加捻，捻度35捻/10 cm，纱线直径接近0.23 cm，采用小样机织制三上一下、五上一下和十五上一下3 种斜纹织物，经密纬密均采用44 根/10 cm。

通过自制的液态水传输测试装置利用图像处理技术对自制试样的液态水传输距离（x、y向）进行测试。

2 结果与分析

2.1 液态水传输形态分析

液态水传输过程中，由于毛细力作用，液态水在机织物上沿x轴或y轴方向不断润湿，出现表面小范围的浸润；同时由于机织物结构间孔隙存在，液态水会随着时间的延长沿纱线间的孔隙逐渐向z轴方向渗漏。机织物结构的差异，使得从孔隙渗漏的水量会有所不同，沿x轴与y轴方向润湿的材料面积也各向迥异，传输一直进行直至水量消耗完毕。

液态水在机织物中的传递主要取决于水对纤维表面的润湿性能、纤维细度和截面形状、纱线间距，改变纤维细度和截面形状、纱线间距，液态水在机织物上传输的形态也会随之改变。通过多物理场仿真软件模拟可得液态水在机织物上随时间铺展所形成的形态，有“单向”“十字”和“椭圆”等典型形态，如图2 所示。其中，椭圆形和十字形如图2（a）和图2（b）所示，为双向传输；图2（c）则为单向传输。这些形态也得到实际试验证实。

从图2 中不难看出，液态水在浮长较小的三上一下织物上呈椭圆形铺展，在浮长较大的十五上一下机织物上呈单向传输。说明材料的结构一定程度上决定了液态水的铺展形态，浮长越小，材料中经纬纱线交织点越多，液态水铺展时可同时接触经纬纱，有利于沿着x、y方向的双向传输，但由于反面传输相对滞后于正面，所以使铺展形态最终呈椭圆形；十字形应该属于椭圆形形态中的特例，改变纱线粗细会使液态水传递形态最终呈十字形，在保持纱线排列密度不变的情况下，纱线越细越不利于液态水在机织物x、y平面的铺展，减少了液态水在经纬纱中浸润的交叉传输，液态水依然双向传输但形态呈十字。机织物浮长越长，液态水要传输到反面浮长的滞后时间加大，液态水在毛细力作用下主要呈现出沿正面浮长方向传输，浮长的加大意味着另一系统纱线接触到液态水的机会减少，液态水最终以浮长方向的纱线为载体铺展，呈现出单向传输形态。

图2 液态水在机织物中的模拟和实际传输形态

2.2 液态水传输距离分析

液态水在织物中的传输能力可以用传输距离进行衡量。当液态水总量一定时，传输距离越大，表明材料对液态水的传输能力就越强，液态水在其中容易完成输送；同时液态水在机织物上的传输沿x轴、y轴与z轴3 个方向进行，但一般会形成差异的传输距离，三者的传输距离变化曲线会形成不同的组合，或者会出现某一方向传输距离明显大的情况。这种认知可能会为液态水在材料中的控制传输提供理论指导。通过多物理场仿真软件模拟可得3 类液态水传输距离变化曲线的组合，如图3 所示。

图3 中，组合1 显示，液态水在y轴方向的传输距离远远超过x、z轴方向，此类组合存在于（二上一下到六上一下）小浮长机织物中，液态水双向传输，浸润形态多呈椭圆形；组合2 表明，沿厚度方向液态水传输距离变化加大，传输距离变大，沿浮长方向传输的最大值变小，x轴小幅上升，此类组合出现在（七上一下到十一上一下）中等浮长机织物中，织物变得相对松软；组合3 显示，就（十二上一下到十五上一下）机织物来说，浮长足够长，交织点少，反面浮长能够接触到液态水的机会少，受此影响铺展形态呈现单向传递，由于长浮长的存在使织物变得松软，织物孔隙易变，液态水可能出现直接渗漏掉下，脱离织物而不参与传输，从而使z轴传输距离变大，甚至与y轴传输距离相当。

通过图3 还可以看出，在x轴方向上，液态水传输距离随时间变化较平稳，各机织物在x轴方向最终传输距离范围在8 mm 到11 mm 之间，说明织物中同一系统互相平行的纱线之间液态水的“跨润”不明显，存在一定阻力；而在沿浮长方向的y轴上，液态水传输距离斜率较陡，数值变化较明显，各机织物在y轴方向最终传输距离范围在18 mm 到32 mm 之间，说明改变织物的浮长对液态水的传输有明显影响，可以考虑通过改变浮长来控制液态水在机织物中的传输。在z轴方向上，液态水传输距离曲线有较平缓和较陡的区段，曲线趋势差别较大，说明织物结构对液态水在厚度方向上的渗漏影响较大，传输距离大约在18 mm 到22 mm 之间不等。事实上，这个传输距离已经超出织物的厚度范围，但能说明液态水自身重量影响其在材料中的传输。

图3 液态水在机织物上传输距离变化

通过模拟仿真试验可以得到如图4 和图5 所示的液态水在各模型机织物上的传输行为。从图4 的传输距离与浮长关系中可以看出，液态水在不同浮长织物上的传输行为具有相似性，同一方向的传输距离曲线走势基本相同，但织物不同方向上的传输存在差异，沿浮长方向的传输距离明显大于其他方向；织物浮长对液态水的传输距离有明显影响，在短浮长时明显存在随着浮长的增加，液态水传输距离有增加的趋势，从二上一下到四上一下斜纹织物，液态水沿浮长方向的传输距离是逐渐增加的，增加浮长有利于液态水的传输，在四上一下斜纹织物中液态水沿浮长方向的传输距离达到最大值（35 mm），当浮长超过一定值时，液态水的传输距离随浮长的增加而逐渐减小，最后达到稳定，说明增加浮长并不会一直增加液态水的传输能力，本研究认为浮长长度选择在4 附近比较合理，可以为机织物中液态水传输控制设计提供一种参考。从图5 的传输距离与时间曲线看，在浮长方向液态水传输距离随着时间延长而逐渐增加，开始增加比较快，经过一定时间的传输后增加减缓，最终达到稳定的最大值；在垂直浮长方向的传输距离相对比较稳定，说明浮长的增加没有改变液态水在纱线间“跨润”的物理条件；在厚度方向的传输距离基本稳定但存在不太明显下降趋势，说明厚度方向以重力为驱动的液态水传输物理条件没有根本性改变，另外浮长的增加可能导致织物的松软和孔隙变大，液态水直接掉下脱离织物而不参加传输。

图4 液态水传输距离与织物浮长的关系

图5 液态水传输距离与传输时间的关系

2.3 液态水传输速度分析

传输速度也是衡量液态水在机织物中传输能力的重要参数。根据仿真模拟结果，绘制二上一下到十五上一下斜纹织物在x、y、z轴方向液态水的平均传输速度，如图6 所示。

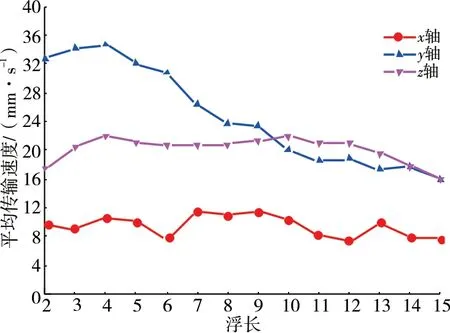
图6 液态水传输速度

从图6 可以看出，液态水在机织物中的传输速度在x轴、y轴、z轴3 个方向存在差异，其中沿浮长方向的y轴方向速度最快，曲线先上升后下降，传输速度先增加后减小，x轴方向和z轴方向速度慢，曲线较平缓，波动小，速度基本稳定。图6 中曲线表明，随着浮长增长，沿y轴方向的传输速度在16 mm/s～35 mm/s 范围变化，变化规律与传输距离相似，明显与浮长有关，存在液态水最大传输距离的浮长；沿x轴传输速度变化范围为8 mm/s～12 mm/s，变化区间不大，传输速度基本稳定，浮长对x轴方向传输速度影响较小；沿z轴传输速度变化范围为16 mm/s～22 mm/s，短浮长时速度随浮长增加有一定增加，在中等浮长时数值相对稳定，在大浮长时，传输速度有所下降，其原因与传输距离变化规律的成因存在相似性。对比3 个方向可以看出，液态水的传输速度存在y轴≥z轴＞x轴，液态水沿浮长方向的传输速度最高可以达到35 mm/s；而当浮长超过某一长度时，随着织物浮长增加，纱线间孔隙越大，液态水沿厚度方向的传输越快，z轴逐渐变为主要传输通道，甚至出现渗漏，此时浮长不再是影响液态水传输距离和传输速度的主要因素。

2.4 模拟结果与实测结果对照分析

通过对三上一下、五上一下和十五上一下3种斜纹织物的模拟仿真和实际测试，可以得到三者沿x轴、y轴液态水的最大传输距离，具体结果如表1 所示。可以看出，模拟结果与实测结果基本接近。其中相对误差最小的是五上一下斜纹织物，其x向相对误差只有8.7%，y向相对误差9.3%，而十五上一下织物相对误差最大，其y向达26.1%，说明本模拟方法对于模拟短浮长织物液态水的传输是有效的。原因可能与纱线模型及测试方法有关，实际纱线是由纤维构成的，液态水不仅会在纱线表面传输，也会在纱线内部传输，而模拟试验建模时纱线是实心的，液态水只在纱线表面传输，显然与实际情况存在差异；另外浮长加长可能会使织物变软，孔隙变化较大，沿厚度方向的渗漏增加，这在模拟试验中是无法反映的，这也可能是十五上一下织物相对误差较大的原因。

表1 最大传输距离结果对照 单位：mm

3 结论

（1）机织物的浮长结构影响液态水传输模式，液态水在机织物上的传输存在“椭圆”“十字”“单向”3 种典型形态。

（2）从传输距离和传输速度方向看，浮长方向是液态水在织物中传输的优先通道，增加浮长有利于液态水在织物中的传输，但传输距离和速度不是一直增加，存在与浮长对应的最大值。

（3）在本研究中四上一下织物拥有最大的传输距离和传输速度，有利于液态水的传输，这对于吸湿快干织物结构的设计提供一种选择依据，控制液态水传输的最佳浮长条件选择在4 左右。

（4）模拟结果与实测结果在传输距离方面具有较好的一致性，尤其适用于模拟短浮长织物液态水的传输。