基于综合分析法的城市需水预测研究

李析男 赵先进 余红敏

摘要：城市需水預测受众多因素的影响，相比利用单一方法进行需水预测，多方法综合预测更能响应多因素的干扰。采用综合分析法预测城市需水，包括资料审查、初步预测、综合预测、需水预测4个阶段。首先，以多种方法对需水定额、社会经济指标等进行预测和检验;其次，采用权重综合评定方法对各种方法进行赋权，并进行相应指标的综合预测;然后，采用传统的定额分析法，对城市需水进行统计;最后，对预测成果进行合理性分析。以贵州省贵安新区为例，预测2020年需水量为20 481.9万m3，2030年为40 902.1万m3，经用水总量符合性分析和用水结构合理性分析，预测结果合理。

关键词：城市需水; 需水预测; 综合分析法; 贵安新区; 贵州省

中图法分类号：TV213.4文献标志码：ADOI：10.15974/j.cnki.slsdkb.2022.05.004

文章编号：1006 - 0081（2022）05 - 0028 - 06

0 引 言

水资源需求预测是对一个区域在未来一定时期内的需水总量（或一个部门、行业需水量）及其时空分配进行推测、估计[1]。合理的城市需水预测对于水资源管理的合理决策起着重要作用。自20世纪60年代开始，美国、日本、英国等国已经开始了全国需水预测，为指导水资源的开发利用提供指导意见。中国的需水预测起源于20世纪50年代，但是主要集中在灌区尺度，其后逐步扩展到区域以及全国范围[2]。根据需水预测的研究目标、预测变量、预测周期、变量选择以及预测尺度，需水预测的常用方法大致可以分为定性和用水定额法、单变量时间序列分析法、滑动平均和指数光滑模型、随机过程模型、时间序列回归模型、场景分析法和决策支持系统、人工神经网络、组合预测法等[3]。上述方法主要是利用城市发展的历史用水资料进行推测。然而，一些城市由于产业结构的调整、不同区域之间的差异等因素的影响，采用单一的需水预测方法可能会有较大偏差，故考虑采用多种预测模型（综合预测模型）进行需水预测，不仅对用水量变动影响因素的解释能力更强，而且预测精度较高[4]。本文建立了综合分析方法基本框架，在资料合理的基础上，通过多种方法对人口和经济进行预测，并采用权重综合的方式，达到多种方法综合的目的，降低多方法间的差异和干扰，最终得到较好的预测结果。采用该综合分析法对需水进行预测可降低单一预测方法的不确定性，同时也弥补多方法之间的影响和差异，为城市需水预测提供了新的思路和方法。

1 综合分析法结构

水资源需求量很大程度反映了一个城市社会经济发展的水平。因此，城市社会经济的相关指标是预测需水量的重要因素。一般来说，社会经济指标包括人口数量、相关产业社会经济产值等，在预测中则采用往年社会经济指标序列来预测未来某年的社会经济指标，进而推算出相关用户的需水量。针对时间序列的特点，本文将综合分析预测方法分为4个阶段，即资料审查、初步预测、综合预测、需水预测，系统结构如图1所示。

1.1 资料审查

资料审查是对资料合理性的检查，需对原始资料进行搜集、提取、处理、再加工。

1.2 初步预测

1.2.1 预测方法

初步预测是对选取的社会经济指标进行拟合和预测，主要包括两个部分：① 人口预测[5]和经济指标拟合;② 结果检验和初始预测。系统选取了人口、经济产值为预测指标，一共选取了9种预测方法进行拟合和预测。本文的人口预测采用Logistics模型、Malthus模型和BP神经网络模型。这3种方法是根据城市最大容量预测不同规划年人口数量，而不是对原始序列进行拟合，其结果检验方式需要结合城市人口的总体规划进行比对。Logistics模型、Malthus模型为经典人口预测模型，应用较广;BP神经网络模型的动态学习能力对人口波动性数据具有较强的识别和拟合能力，能够克服以往人口预测模型剔除奇异值或划分阶段处理的缺陷[6]。经济预测在计算机软硬件不断更新以及现代数学方法不断完善的基础上，形成了很多种类的预测方法[7]。根据实际问题的需求，本文经济指标的拟合采用灰色模型、多项式模型（1～3次）、指数模型、对数模型、ARMA模型和NAR神经网络模型[8]，这6种方法分别采用各自的检验方法进行比选，通过检验则进入初始预测，否则返回资料审查阶段重新开始;通过检验但初始预测结果不合理，则直接剔除该预测方法，若所有方法均不合格，则选取其他预测模型进行预测分析。

1.2.2 初步预测结果检验

传统的需水预测是选取某一方法预测值作为最终结果，或者对比分析若干方法的预测结果，选取较为合理的预测值作为最终结果。但也存在一系列问题：① 如果是两种或两种以上预测方法拟合效率都较高时，还没有明确的分析方式来确定某个方法模拟效果最佳，尤其各种方法拟合结果差异较大时，则无法解释未来预测结果的优劣;② 如果只有一种预测方法的拟合效率较高，则单一方法对未来预测的优劣难以评定。所以，应采用多种方法进行初步预测，并选取通过检验的几种方法进行综合预测。

1.3 综合预测

综合预测是对初步预测结果进行综合，其基本思想是对已通过检验的预测方法赋权，以权重为依据，综合各个方法预测值的权重，得到最终预测指标的目标值，即多种预测方法权重值与指标值的乘积之和。

1.3.1 权重分析

赋权方法主要采用变差系数法、熵权法、标准/平均差法、CRITIC法（Criteria Importance Through Intercriteria Correlation，CRITIC）等。

（1） 变差系数法也叫变异系数法[9]（Coefficient of variation method），是直接利用各项指标所包含的信息，通过计算得到指标的权重，是一种客观赋权的方法。该方法的基本做法是：在评价指标体系中，指标取值差异越大的指标，也就是越难以实现的指标，这样的指标更能反映被评价单位的差距。

（2） 熵权法的基本思路是根据指标变异性的大小来确定客观权重[10]。

（3） 标准/平均差法思路与熵权法相似。通常某个指标的标准差越大，表明指标值的变异程度越大，提供的信息量越多，在综合评价中所起到的作用越大，其权重也越大。相反，某个指标的标准差越小，表明指标值的差异程度越小，提供的信息量越少，在综合评价中所起到的作用越小，其权重也应越小[11]。

（4） CRITIC法[12]是一种以指标之间的对比强度和冲突性来综合衡量其权重的客观权重赋值方法。该方法不仅考虑到指标所包含信息量大小对权重的影响，还考虑了不同方案的对比强度以及各项指标之间的冲突性，更为客观。

为了在评价中既反映决策的主观性，又体现决策的客观性，需要对上述各指标的主客观赋权进行集成。本研究采用沈阳武等[13]提出的基于最优组合权重的电能质量灰色综合评价方法作为权重综合评定方法。该方法是一种兼顾主客观因素的集成赋权方法，可以提高综合评价的科学性。

1.3.2 指标预测

指标预测是对初始预测中通过检验的模型预测结果进行综合，通过变差系数法、熵权法、标准/平均差法和CRITIC法计算各个已通过检验的模型预测结果权重，再对上述各指标的权重进行集成，得到各权重评价方法的综合权重。综合权重值代表该模型在预测中所占的比重，并乘以相应的预测值，求和之后即为综合预测结果。

在中国水资源规划中，广泛采用分产业的预测方法，分为生活用水、生产用水和生态用水等，分别研究不同产业用水变化规律，对未来用水目标进行预测。

2 实例分析

贵安新区地处贵州省贵阳、安顺两市之间，是中国第8个国家级新区，规划范围包括贵阳、安顺下辖清镇市、花溪区、西秀区、平坝县的20个乡镇及5个社区，规划总面积为1 795 km2，行政区总面积为1 895 km2。

本研究来源于《贵州贵安新区总体规划（2013-2030）水资源论证》，规划期限为2013～2030年，基准年为2012年、近期为2013～2020年、远期为2021～2030年。贵安新区2012年常住人口75万，其中，城镇人口约31万，城镇化率41%。

2.1 资料审查

本文数据来源包括：贵州省统计年鉴（2000～2012年）、贵州省水资源公报（2000～2012年）、贵阳市统计年鉴（2002～2012年）、贵阳市水资源公报（2002～2012年）、安顺市统计年鉴（2004～2012年）、安顺市统计年鉴（2004～2012年）。农业经济和非农业经济产值通过面积比例统计而得，各类用水定额以贵阳市为标准进行统计，成果详见表1，2。

2.2 初步预测

2.2.1 人口预测

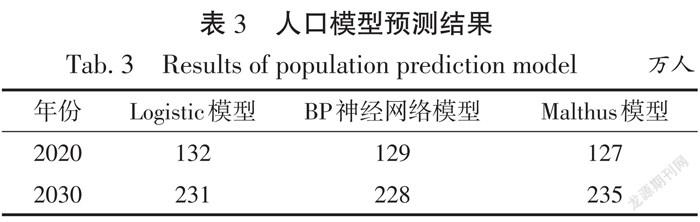
3种模型的初始人口预测过程不赘述，结果详见表3。Malthus模型和BP神经网络模型能较好地验证Logistic模型的预测结果，还需对上述3种模型结果进行综合预测。

2.2.2农业经济预测

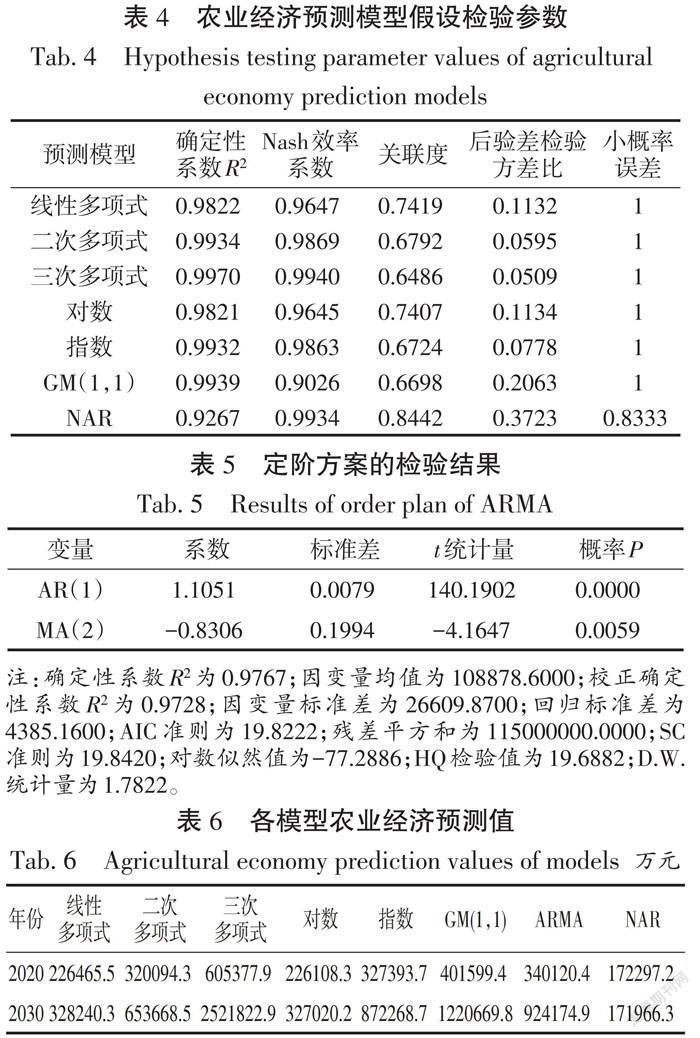
拟采用8种模型对农业经济进行预测（表4，5），并进行假设检验。根据检验结果，选择通过检验的模型进行预测，预测结果见表6。

根据贵安新区城市总体规划，在规划年将实现从传统农业向都市农业的转型，种植结构的优化及发展模式的变化将促进其逐年增长，而NAR模型预测结果呈现出农业经济总值随着时间变化而减小的趋势，与实际情况不符，故认为该法预测有误，在综合预测时不考虑该法。

.2.3 非农业经济预测

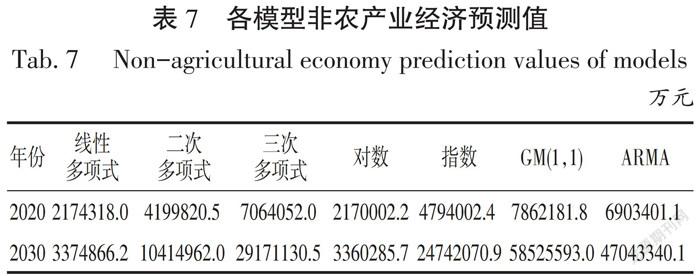
与农业经济预测过程相类似，方法及成果不再赘述，7种模型皆通过检验，结果详见表7。

2.2.4 定额预测

定额预测与上述流程一致，方法及成果不再赘述，（非）农业用水定额的模型预测结果见表8。对居民生活用水定额进行预测时，ARMA模型和NAR模型通过了检验，故选取这2个模型进行预测，结果见表8。

对于各用户定额预测，有如下结论：① 方法检验不通过，则不采用该模型进行预测;② 检验通过的模型，预测结果发现如出现负值等明显错误的，不选取其结果作为综合预测的依据。

2.3 综合预测

对研究区域的人口数量、农业经济值、非农业经济值及其定额等指标进行综合预测，为了降低权重计算误差，在权重综合计算中更能体现各指标值增长阶段性变化规律，故将各模型初始预测结果分为两个阶段进行权重分析和指标预测。其中，以2013～2020年预测值为第一段，2021～2030年预测值为第二段。各指标在不同预测模型下的权重值，见表9，再结合表6～8的各指标值，得到最终的指标预测值。

（1） 人口预测。2013～2020年Logistic模型预测结果、BP神经网络模型预测结果、Malthus模型预测结果的综合权重分别为0.355 1，0.306 2，0.338 7，则2020年人口预测值为129.4万人。2021～2030年Logistic模型预测结果、BP神经网络模型预测结果、Malthus模型预测结果的综合权重分别为0.308 0，0.315 2，0.376 8，則2030年人口预测值为231.6万人。

（2） 农业经济预测。2020年为389 870.1万元，2030年为1 162 513.2万元。非农产业经济预测，2020年为5 661 613.2万元，2030年为34 169 332.6万元。农业用水定额预测，2020年为107.7 m3/万元，2030年为25.9 m3/万元。非农产业用水定额预测，2020年为11.6 m3/万元，2030年为4.7 m3/万元。居民生活用水定额预测，2020年为118.5 L/（人·d），2030年为117.3 L/（人·d）。

（3） 对于居民生活用水定额，考虑到预测模型所参考原始序列均为居民生活用水净定额，根据CJJ 92-2002《城市供水管网漏损控制及评定标准》，取管网漏损率为10%进行居民生活用水毛定额的计算，得出贵安新区2020年和2030年居民生活需水毛定额分别为131.6 L/（人·d），130.3 L/（人·d）。

2.4 需水预测

采用农业经济定额法，经预测：2020，2030年农业经济产值分别为39.0亿元和116.3亿元，2020，2030年经济定额分别为166.7 m3/万元和83.3 m3/万元，则2020，2030年农业多年平均灌溉用水总量分别为6 498.9万m3和9 679.9万m3。

采用非农产业经济定额法，贵安新区2020，2030年非农产业经济定额分别为11.8 m3/万元和5.3 m3/万元，非农产业经济2020，2030年分别为566.2亿元和3 416.9亿元，则非农产业2020，2030年总需水量分别为6 680.0万m3和18 262.4万m3。

贵安新区绿化浇洒（环境）需水量采用人均面积定额法，人均绿地面积为11.5 m2，定额均为2.0 L/（人·d），以365 d计，2020，2030年的河道外需水量分别为1 086.3万m3和1 944.3万m3，详见表10。

2.5 合理性分析

2.5.1 用水总量符合性分析

根据《贵州省人民政府办公厅关于贵州贵安新区用水总量控制目标的函》（黔府办函【2015】115号），贵州省人民政府承诺待新区水资源论证审查后，在不突破国家下达给贵州省用水总量控制目标基础上，从全省范围内统一调剂用水总量指标。贵安新区初步确定的用水总量指标2020年和2030年分别为3.18亿m3和4.27亿m3，本预测成果在用水总量红线要求以内，基本符合用水总量控制要求。

2.5.2 用水结构合理性分析

现状2012年农业用水占比最高，2020年和2030年非农产业用水占比最高。贵安区作为一个经济开发的新区，早期发展以农业为主，中期人口大幅度入住，导致生活用水占比增加，在经过一段发展后，农业逐渐转变为非农经济，故非农产业用水逐渐增高，符合产业结构调整的要求，用水结构合理。贵安新区需水量结构见表12。

综上所述，本次需水预测成果基本合理。

3 结论与展望

本文介绍了城市需水预测的综合分析方法及其基本结构和技术方法。基本结构包括资料审查、初步预测、综合预测、需水预测等。技术方法分为初步预测方法和综合预测方法。在初步预测中，人口預测采用了3种人口预测模型，经济拟合采用了6种预测模型。在综合预测中，采用了4种权重分析方法及其综合评定法。在预测过程中，采用了人口数量、农业经济指标、非农业经济指标、居民人口用水定额、农业定额、非农业定额等指标，同时对各种预测方法的合理性进行检验、对比和分析，为城市需水预测提供了方法和思路。

基于综合分析法的需水预测是以数理统计学为基础，结合城市规划开展工作的。在实际应用中，需理论与实际相结合，结合区域发展和定位，对成果综合分析，才能得到较为合理的最终成果。该综合分析方法在初步预测时分为人口和经济预测，选取了9种模型，在未来工作中应根据实际需求选取更多的模型。

本文是作者2016年在贵安新区建设初期，结合城市发展规划的研究成果，基准年是2012年，规划年分别为2020年和2030年，作为方法研究，该成果可以为预测提供科学依据。随着时间的发展，贵安新区因政策导向和实际情况的影响，2020年预测值与实际值有较大差异。作为研究人员，这是未来需要面对的课题。基于此，城市需水的预测值与实际值的差异和成因将是下一步研究工作的要点。

参考文献：

[1] 吕孙云.基于断面控制的汉江流域水资源多目标调配研究[D].武汉：武汉大学，2013.

[2] 贺丽媛，夏军，张利平.水资源需求预测的研究现状及发展趋势[J].长江科学院院报，2007，24（1）：61-64.

[3] EA Donkor， TA Mazzuchi， R Soyer， et al. Emmanuel A Donkor-urban water demand forecasting： review of methods and models [J]. Journal of Water Resources Planning & Management， 2014，140（2）：146-159.

[4] 刘秀丽，邹庆荣.我国用水总量预测研究[J].系统科学与数学，2016，36（10）：1643-1651.

[5] 张海峰，杨萍，李春花，等. 基于多模型的西宁市人口规模预测[J].干旱区地理，2013，6（5）：955-962.

[6] 吴劲军.基于BP神经网络的人口预测模型研究[J].统计与信息论坛，2004，19（2）：44-46.

[7] 余伟.经济模型的构建与预测方法的研究[D].广州：华南理工大学， 2012.

[8] 李析男，王宁，梅亚东，等.NAR神经网络的应用与检验——以城市居民生活需水定额为例[J]. 灌溉排水学报，2017，36（11）：122-128.

[9] 刘杰，达列雄.基于变差系数法的水污染物总量分配模型[J].陕西理工学院学报（自然科学版），2014，30（3）： 74-78.

[10] 杨力，刘程程，宋利，等.基于熵权法的煤矿应急救援能力评价[J].中国软科学，2013（11）：185-192.

[11] 罗赟骞，夏靖波，陈天平，等.网络性能评估中客观权重确定方法比较[J].计算机应用，2009，29（10）：2624-2631.

[12] 张立军，张潇.基于改进CRITIC法的加权聚类方法[J].统计与决策，2015（22）： 65-68.

[13] 沈阳武，彭晓涛，施通勤，等.基于最优组合权重的电能质量灰色综合评价方法[J].电力系统自动化，2012，36（10）： 67-73.

（编辑：李 慧）

Study on urban water demand forecasting based on comprehensive analysis method： case of Gui'an New Area of Guizhou Province

LI Xinan1，2， ZHAO Xianjin1，2， YU Hongmin1，2

（ 1. Guizhou Water & Power Survey-Design Institute Co.，Ltd.， Guiyang 550002， China; 2. Guizhou Engineering Technology Research Center for Exploitation and Utilization of Water Resources in Karst Region， Guiyang 550002， China）

Abstract： Urban water demand forecasting is influenced by many factors， and a multi-method integrated forecast can response more to the interference of multiple factors than a single method for water demand forecasting. The urban water demand forecasting was carried out by using the integrated analysis method， which included four stages， data review， preliminary forecast， integrated forecast and water demand forecast. Firstly， the water demand quotas and socio-economic indicators，etc. were predicted and tested by various methods; secondly， the weighted comprehensive assessment method was used to assign weights to various methods and make comprehensive forecasts of corresponding indicators; thirdly， the traditional quotas analysis method was used to make statistics on urban water demand; finally， the forecast result rationality were analyzed. Taking Gui'an New Area in Guizhou Province as an example， the water demand was 204.819 million m3 in 2020 and 409.02 million m3 in 2030. The analysis of the conformity of the total water consumption and the rationality analysis of the water consumption structure showed that the prediction results were reasonable.

Key words： urban water demand; water demand forecasting; comprehensive analysis method;  Gui'an New Area; Guizhou Province

收稿日期：2020-06-11

基金項目：贵州省科技计划项目（黔科合支撑[2019]2879，黔科合支撑[2021]一般467）

作者简介：李析男，男，博士，高级工程师，研究方向为水资源规划与管理。E-mail：lixinan1985@126.com

通讯作者：余红敏，女，工程师，研究方向为经济评价。E-mail：991807665@qq.com