基于R+(3-CPR)+U混联机构的四足机器人运动学分析及轨迹规划
高海豹,李瑞琴,李泽辉,宁峰平
(中北大学机械工程学院,山西 太原 030051)
由拖拉机等农业机械产生的土壤压实问题越来越明显[1],在一定程度上限制了农作物根系的生长,对提高农作物产量产生了不利影响[2-3]。从几何角度考虑,轮式拖拉机与地面的接触形式为圆柱(轮胎)与平面(地面)相切,与地面的接触面积较小,加剧了对土壤的压实。履带式拖拉机与地面的接触形式为平面(履带)与平面(地面)接触,接触面积相对较大,缓解了对土壤的压实,但履带式拖拉机避障能力差,如不能跨越输水管道等。为解决上述问题,本文基于R+(3-CPR)+U串并混联机构设计了一种四足移动机器人,机器人在移动过程中足端与地面保持平行,可减缓对土壤的压实。串并混联机构兼具并联机构和串联机构的优势,在足式移动机器人领域的应用越来越多[4-5]。王晓磊等[6]设计了一种串并混联四足移动机器人,采用 Lagrange 方程建立了机器人腿部的动力学模型,对该机器人进行了动力学分析;高建设等[7-8]通过3-RRR机构串联转动机构作为机器人的腿部结构,设计了一种四足移动机器人,采用D-H法求解了机器人腿部机构的位置反解,并通过ADAMS软件进行了动力学仿真分析;田兴华等[9]设计了3种三自由度串并混联机构,分别对3种构型的工作空间、承载空间、各向同性度进行了对比分析;马广英等[10]设计了一种两转两移的混联腿部机构,对其进行了运动学分析和步态规划。本文运用螺旋理论对R+(3-CPR)+U混联机构的自由度进行分析,通过连续的RPY坐标变换求解该机构的位置逆解,采用三维动态法对该机构的工作空间进行分析,并对所设计的四足机器人进行稳定性分析和轨迹规划。
1 整体构型设计
如图1所示,四足机器人由机器人主体和4条腿构成,每条腿的腿部结构完全相同,均为R+(3-CPR)+U混联机构。大腿为3-CPR并联机构,通过3-CPR并联机构中的平台1与机器人主体的转动轴形成R副进行连接,小腿为刚性结构,大腿与小腿之间通过U副连接。
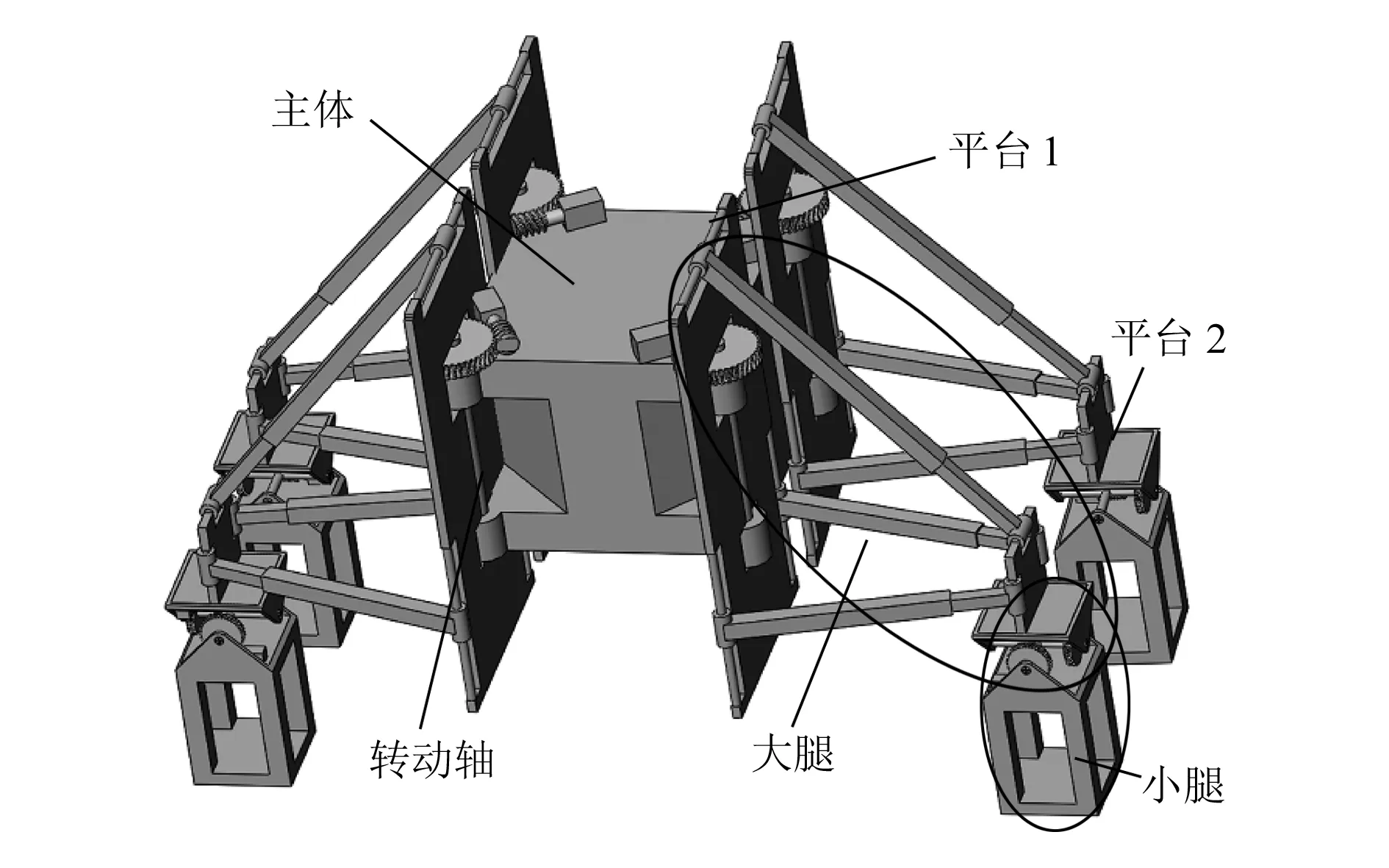
图1 基于R+(3-CPR)+U混联机构四足机器人
2 R+(3-CPR)+U混联机构自由度分析
由于机器人4条腿的结构完全相同,因此以其中的一条腿为研究对象,分析机器人腿部机构的自由度。基于R+(3-CPR)+U混联机构的四足机器人腿部机构构型如图2所示。
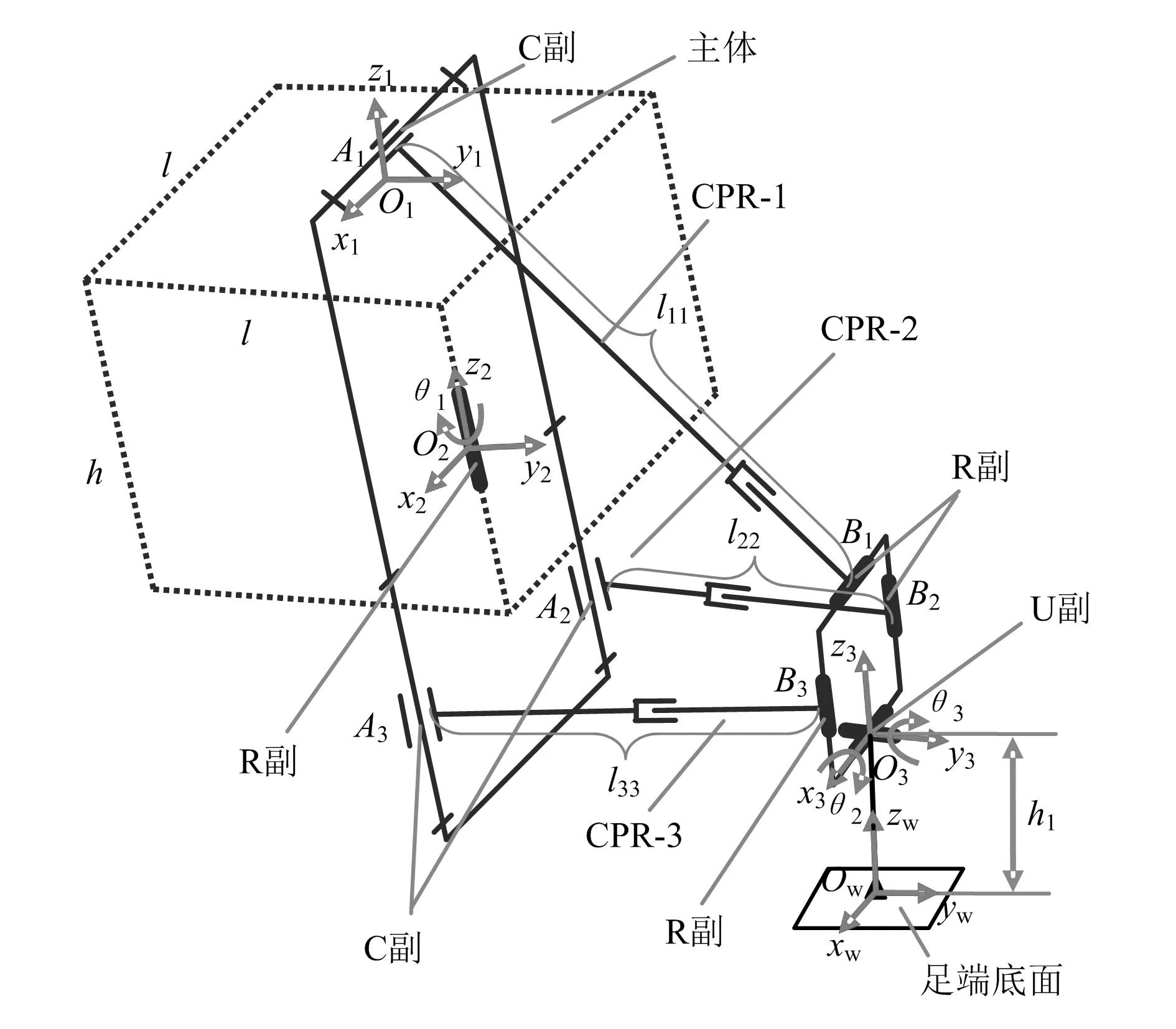
图2 R+(3-CPR)+U混联机构构型
为方便计算和对分析过程进行描述,建立机构坐标系,如图2所示。图中虚线部分为机器人主体,其形状为l×l×h的长方体,运动副位置用字母表示。以机器人主体上端面形心O1为原点,建立坐标系O1-x1y1z1(标记为{O1}),z1轴垂直于上端面,正方向竖直向上,y1轴水平,正方向向右,x1轴由右手螺旋定则确定;以机器人主体竖直棱线中点O2为坐标原点,建立坐标系O2-x2y2z2(标记为{O2}),与平台1固连,z2轴与对应棱线重合,正方向竖直向上,y2轴水平,正方向向右,x2轴由右手螺旋定则确定;以平台2连接U副的一边的中点O3为原点,建立坐标系O3-x3y3z3(标记为{O3}),与平台2固连,x3轴与该边重合,其方向与x2轴相同,z3轴与平台2平行,正方向竖直向上,y3轴由右手螺旋定则确定;以足端底面形心Ow为坐标原点,建立坐标系Ow-xwywzw(标记为{Ow}),zw轴垂直于足端底面,正方向指向O3,OwO3为小腿的长度h1,yw轴与y3轴方向相同,xw轴由右手螺旋定则确定。Ai(i=1,2, 3)表示混联机构中C副的位置,Bi(i=1, 2, 3)表示混联机构中R副的位置。3-CPR并联机构中平台1和平台2的尺寸及运动副位置,如图3所示,其中平台2的形状为正方形,所连接的运动副分别位于相应边的中点处。
当四足机器人以“3+1”步态行走时,3条支撑相的腿与机器人主体共同支撑摆动相的腿,因此在分析腿部运动时,可将机器人主体视为固定不动的“机架”,将坐标系{O1}视为固定坐标系。坐标系{O1}下整个腿部机构中能够影响足端底面运动的运动螺旋如下。

图3 平台尺寸及运动副位置
平台1与机器人主体之间形成的转动副的运动螺旋为:
S/1=(0 0 1;ab0)
(1)
式中:a,b为运动螺旋的参数,与运动副的方向和位置有关。
为简化分析过程,可将3-CPR并联机构视为一个特殊的运动副,这个特殊的运动副使平台2相对平台1在空间中做三维平移运动[11],因此其运动螺旋为:
S/2=(0 0 0;1 0 0)
S/3=(0 0 0;0 1 0)
S/4=(0 0 0;0 0 1)
(2)
大腿与小腿之间的U副的运动螺旋为:
S/5=(1 0 0;0cd)
S/6=(0 1 0;e0f)
(3)
式中:c,d,e,f为运动螺旋的参数,与运动副的方向和位置有关。
式(1)、(2)、(3)共同构成了四足机器人腿部机构的运动螺旋系,求得该运动螺旋系的秩为6,因此该机构共有三转三移6个自由度,理论上足端底面可达到空间中的任一位置和位姿,与少自由度腿部机构相比,具有更大的灵活性。
综上,基于R+(3-CPR)+U混联机构的四足机器人腿部机构的自由度,能够使该四足机器人移动时足端底面与地面保持平行,满足四足机器人移动时的动作要求。
3 R+(3-CPR)+U混联机构位置逆解
机构的位置逆解为已知执行端上确定一点的位置和位姿,求解机构中各输入参数的过程。R+(3-CPR)+U混联机构的输入参数为θi(i=1,2,3)和lii(i=1,2,3)。其中,θ1为平台1与机器人主体之间的角度,θ2为U副中与x3轴重合的转动轴的转动角度,θ3为U副中与y3轴重合的转动轴的转动角度;l11为A1B1的长度,l22为A2B2的长度,l33为A3B3的长度。R+(3-CPR)+U混联机构的执行端即为足端,选取足端底面的形心Ow作为参考点,已知在固定坐标系{O1}下该点的位置和位姿为(x,y,z;α,β,γ),求解的输入参数θi(i=1,2,3)和lii(i=1,2,3)即为位置逆解。
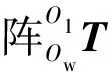
(4)
式中:c表示cos,s表示sin。
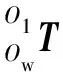
(5)
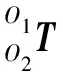
(6)

(7)


(8)
由式(5)~(8)可得:
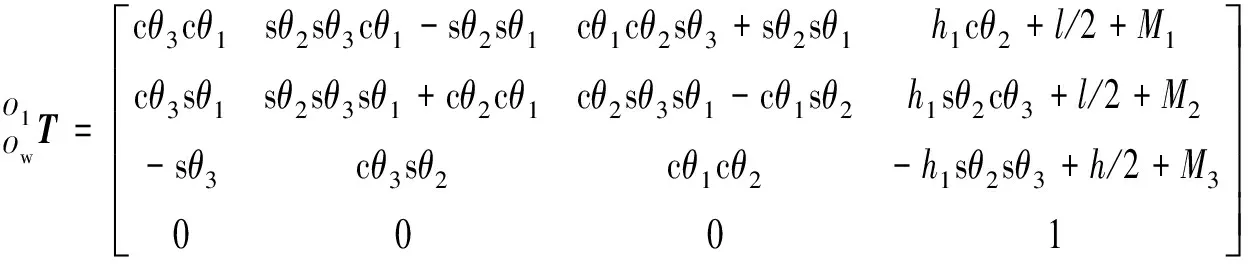
(9)
将式(4)等于号右侧矩阵与式(9)等于号右侧矩阵对应项相等,经计算可得:
(10)
式(10)即为R+(3-CPR)+U混联机构的位置反解。
4 R+(3-CPR)+U混联机构工作空间分析
工作空间是指机构中执行端的工作范围,是衡量机构运动性能的重要指标之一。采用三维动态法对该机构的工作空间进行求解。机器人结构参数设定:l=600 mm,h=500 mm,l1=1 040 mm,l2=520 mm,l3=360 mm,l4=200 mm,h1=300 mm。驱动参数变化范围设定:θ1为0~0.5π,θ2为-0.167π~ 0.167π,θ3为-0.167π~ 0.167π,l11为750~1 280 mm,l22为520~920 mm,l33为520~920 mm。将运动副约束关系和机器人的结构尺寸导入MATLAB软件中,通过给各驱动副添加相应驱动参数,绘制坐标系{O1}下以足端底面形心Ow为参考点的工作空间,如图4所示。
由图4可知,该机构工作空间保持连续,无空洞,将R+(3-CPR)+U混联机构作为足式机器人腿部,能够使机器人足端在空间中连续运动,有利于对足式机器人进行足端轨迹规划和移动路径规划,提高足式机器人在农田等复杂环境下的通过性。

图4 R+(3-CPR)+U混联机构工作空间
5 稳定性分析
稳定裕度是指机器人质心在支撑区域的投影到支撑区域边界的最短距离di,是判别机器人稳定性的重要指标之一。当四足机器人以“3+1”步态行走时,4条腿中3条腿作为支撑相形成支撑区域,另一条腿作为摆动相,腿部抬起,足端脱离地面进行运动。为方便分析,对机器人的相关参数作如下设定:机器人一条腿的质量为m,且分布在平台1形心处的质量为0.5m,足端形心处的质量为0.5m;机器人主体的质量为2m,质心与形心重合;足端形状为Lmm×Lmm的正方形,机器人初始状态下四足呈L1mm×L2mm的矩形分布,如图5所示。

图5 稳定裕度分布
由于四足机器人的结构具有对称性,因此机器人的整体质心在地面上的投影M位于支撑区域的形心上,即在4个足形成的L1mm×L2mm的矩形对角线交点上。以对角线交点作为原点建立地面坐标系O0-x0y0。当机器人以足1作为摆动相时,足2、足3、足4则会形成支撑区域,如图5中虚线区域所示,此时机器人的稳定裕度SM为:
SM=min(d1,d2,d3)
(11)
由图5中的几何关系可计算出d1,d2,d3的值为:
(12)
式(11)、(12)可用于分析机器人足端尺寸与稳定性的关系,当SM趋于0时,机器人质心处于支撑区域边缘,机器人处于将要倾倒的临界状态,稳定性较差。
由图5可知,机器人在y0轴正方向上的稳定裕度SM=d4,假设足端工作空间足够大,机器人采用“3+1”步态,在y0轴正方向上的最大步距为lymax,与稳定裕度SM有如下关系:
(13)
由图5中的几何关系可求得d4的值为:
(14)
根据式(13)、(14),可得y0轴正方向上最大步距lymax与足端尺寸L的关系为:
(15)
同理可得,x0轴正方向上最大步距lxmax与足端尺寸L的关系为:
(16)
由以上分析得到的足端尺寸L与稳定裕度SM、最大步距lymax和lxmax之间的关系,对机器人足端轨迹规划和路径规划具有重要的参考价值。
6 足端轨迹规划
6.1 足端轨迹设计
基于R+(3-CPR)+U混联机构四足机器人,以农田作为主要应用场景,根据机器人在田间移动时足端的动作特征,对机器人足端轨迹进行规划。
将机器人足端轨迹分为3段,构造出一种直线与半周期上凸正弦曲线相结合的复合足端轨迹,如图6所示。A点为机器人足端抬起之前的支撑点,D点为目标落脚点。抬脚阶段,足端由A点沿直线运动至B点,线段AB垂直于A点处的地面;伸出阶段,足端由B点运动至C点,并将足端底面调整至与目标落脚点D处的地面平行,BC之间为半周期上凸正弦曲线;落脚阶段,足端由C点沿直线运动至D点,线段CD垂直于D点处的地面。
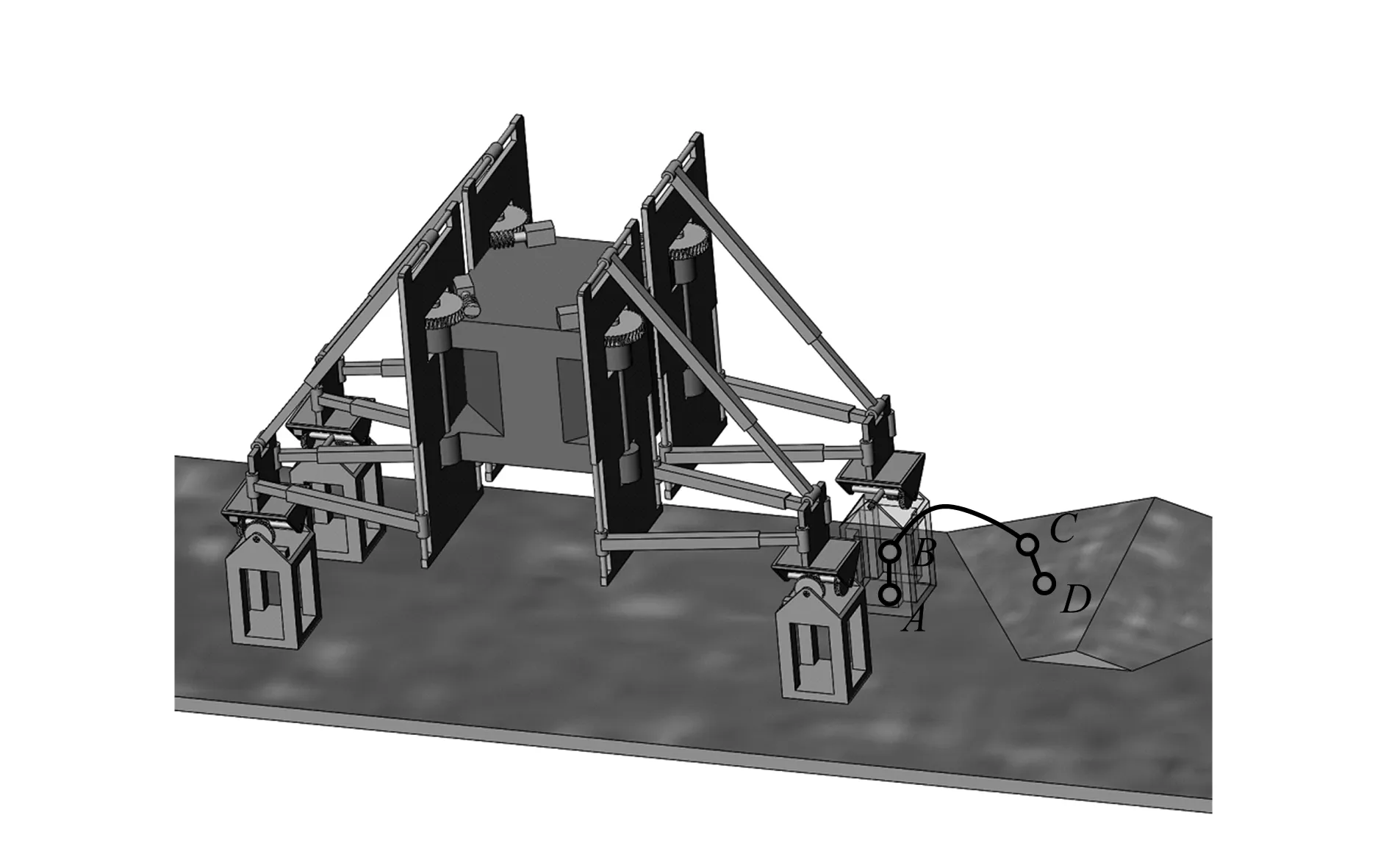
图6 足端轨迹
设A点的位姿为(xA,yA,zA;αA,βA,γA),D点的位姿为(xD,yD,zD;αD,βD,γD),AB的长度与CD的长度相等为H1,BC正弦曲线最高点距离地面的高度为H2。由几何关系可得线段AB、正弦曲线BC、线段CD的解析式。
线段AB的解析式为:
(17)
线段CD的解析式为:
(18)
正弦曲线BC的解析式为:
(19)
式(19)中涉及的B点和C点坐标,可由式(17)和式(18)解出。当x=xA+H1cosαA时,可由式(17)解出B点坐标,当x=xA+H1cosαD时,可由式(18)解出C点坐标。
直线与正弦曲线结合的复合足端轨迹,对突起地形具有良好的通过性,有利于机器人在农田等复杂环境下移动。
6.2 足端轨迹仿真
运用SolidWorks软件对足端轨迹进行运动学仿真,具体过程如图7所示。图7(a)所示为机器人的初始状态,图7(b)所示为机器人完成抬脚动作时的状态,图7(c)所示为机器人完成伸脚动作时的状态,图7(d)所示为机器人完成落脚动作时的状态。机器人采用“3+1”步态时,依次控制每个足重复图7所示的过程,从而使机器人整体向前移动。
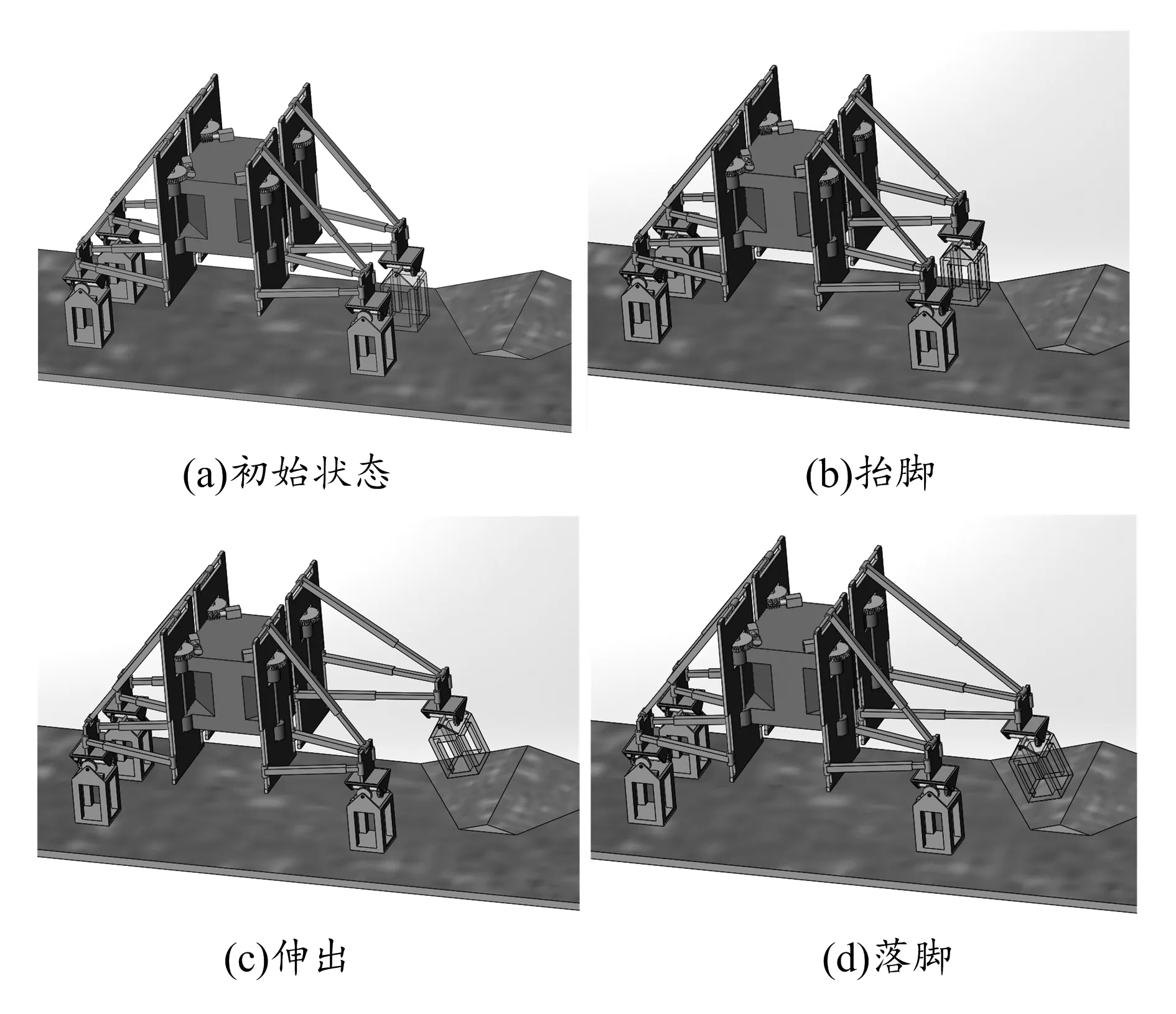
图7 足端运动过程
机器人的结构尺寸参数与第4章的设定相同,足端尺寸为180 mm×180 mm。轨迹参数设定:H1=150 mm,H2=320 mm,足端抬起前支撑点A的位姿为(0,0,0;0.1π,0.1π,0),目标落脚点D的位姿为(50,300,50;0.12π,0.08π,0),即步距为308.2 mm,足端运动的最大高度为320 mm,y方向上的最大位移为300 mm。通过式(17)~(19)可解出机器人运动过程中的足端轨迹曲线,如图8(a)所示。将机器人足端运动过程中的驱动参数θi(i=1,2,3),lii(i=1,2,3)导出,如图9所示。
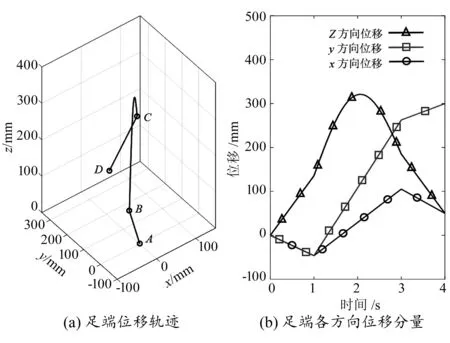
图8 足端位移轨迹和各方向位移分量
仿真得到足端轨迹如图8(a)所示,各方向位移如图8(b)所示。足端在0—1 s由A点沿直线运动至B点,足端进行平移运动,由图9可知,在该过程中驱动参数l11,l22,l33发生变化,θ1,θ2,θ3不变,说明在0—1 s只有l11,l22,l33对足端进行了驱动;1 s—3 s足端由B点沿半周期上凸正弦曲线运动至C点,在该过程中θ2,θ3也参与驱动,对足端位姿进行调整,使C点位姿与D点位姿相同;3 s—4 s足端由C点沿直线运动至D点,由图9可知,该过程是在l11,l22,l33驱动下进行的。综上,足端空间中的平移运动在l11,l22,l33的驱动下进行,位姿调整在θ1,θ2,θ3的驱动下进行,平移运动和位姿调整可同时进行。

图9 驱动副参数θ1,θ2,θ3,l11,l22,l33随时间变化图
由图9还可以看出,驱动参数的变化曲线连续、无断点,证明该机器人能够以6.1节设计的复合足端轨迹进行移动。另外驱动参数曲线无明显突变,说明驱动副的线速度、角速度无剧烈变化,不会对机器人本身产生强烈冲击,进一步证明了复合足端轨迹作为机器人足端运动轨迹的可行性。
7 结束语
本文R+(3-CPR)+U混联机构具有三转三移6个自由度,且工作空间连续,无空洞,有利于机器人足端在空间中进行连续运动;机器人能够以直线与正弦曲线相结合的复合足端轨迹进行运动,且稳定性良好;以R+(3-CPR)+U混联机构为腿部的四足机器人,在运动过程中能够使足端底面与地面平行接触,减缓对地面的压实。

