有限水域近水面气流演化特征试验研究*

高 昂，吴修锋，吴时强，戴江玉，王芳芳，吴晨晖

(1：南京水利科学研究院，水文水资源与水利工程科学国家重点实验室，南京 210029) (2：水利部太湖流域水治理重点实验室，南京 210029)

全球71个典型湖泊研究结果表明，自1980s以来全球湖泊蓝藻“暴发”整体呈加剧趋势，水环境污染及水生态退化是湖泊面临的普遍问题[1]. 秦伯强[2]在回顾太湖治理历程的基础上，发现目前湖沼学研究与湖泊物理环境和过程的结合度不够，指出未来应深化空气动力学、水动力学与生物地球化学等多学科交叉研究. 对于大多数湖泊而言，气流是湖泊水体的主要驱动力之一，水气相互作用对大气与湖泊之间能量与物质传递至关重要[3]. 比如，当风速大于某一临界值时，湖泊水面的气体(如CO2、CH4等)传输速率与风速呈显著正相关[4-5]，然而，不同研究得到的风速-气体传输速率之间的关系存在较大差异，造成这种差异的主要原因之一是不同研究使用的风速测点高度不同(同一测线不同高度处风速不同). 为了减小这种差异，部分研究采用风速廓线公式外延计算得到水面上方10 m高度处风速u10，并建立u10与气体传输速率的关系. 然而，对于面积有限的湖泊而言，摩阻风速u*和特征粗糙度z0与风速和吹程有关[3]，导致使用风速廓线公式过程中选取u*与z0时存在经验性，仍会造成风速-气体传输速率关系的不确定性. 可见目前对湖泊水域气流动力参数选取方面还未达成一致，需要通过近水面气流演化特征的研究进一步明确.

湖泊水域面积有限，属于有限水域，水体在气流驱动下产生风浪和风生流[6]，两者随风速和吹程增加逐渐演化，如风浪尺度与动力强度的增加[7]，风生流强度与风生环流模式的改变[8]等. 相应地，气流在与水流耦合作用过程中也逐渐演变，如风速随吹程的增加[9]，气流边界层的逐渐发展[10-11]等. 近水面气流演化特征研究属于边界层流动问题，一直是海洋、湖泊领域关注的热点[12-13]，但由于风浪的非恒定特征，近水面气流特征比平板气流更加复杂，其研究更具挑战性. 湖面风场的不均、不稳特点使得现场观测多具短历时、点测量特征，获取的数据系统性较差，制约了对湖面气流演化特征的深入研究. 风洞水槽因具有精细可控的优势，一直是水气作用规律研究的重要手段[14]. Liberzon和Shemer[9]、Longo[10]、Shaikh和Siddiqui[15]等通过试验研究了水气相互作用规律，阐述了水-气相互作用与气-平板相互作用之间的异同，发现风浪的存在增加了气流下垫面的粗糙度，剖析了不同风浪尺度对气流特征的差异影响，发现近水面一定高度内时均风速随着距离水面降低而快速减小[15]，即近水面气流存在明显的风浪扰动区(波致气流边界层)，该区域内水气作用强烈，是能量与物质交换最强烈的区域，也是水气作用研究中重点关注的区域，其中，波致气流边界层厚度δwind的确定是主要研究内容之一. 然而，但不同研究对δwind的判定存在差异，Sullivan等[16]试验研究发现小风速时δwind为主频波长Ld的0.16倍，而Liberzon和Shemer[9]的试验结果表明δwind为Ld的0.32倍，Zavadsky和Shemer[17]发现大风速时δwind可增大至Ld的0.48倍. 可见，目前多认为波致气流边界层厚度是主频波长的单一函数，但不同研究结果却未达成一致. 这就会给气象与环境监测带来难题，可能导致在湖面架设气象、环境等监测仪器时存在架设高度的不确定性，如测点架设在边界层以上，测量的数据可能不具代表性，且具有误导性. 因此，需理清水面波致气流边界层厚度与风浪尺度的关系，以指导湖泊、湿地等有限水域气象与环境监测.

有限水域气流动力参数选取不明与波致气流边界层厚度不清的现状彰显了目前湖泊水环境与湖泊动力的交叉研究还存在短板，其中，湖面近水面气流作为湖泊主要动力条件，研究近水面气流演化特征是补充上述短板的关键前提. 基于此，本研究以湖泊、湿地等有限水域为研究对象，在风洞水槽中模拟研究有限水域近水面气流演化特征. 首先，从时间域和频率域两个维度对风速垂向分布、摩阻风速、特征粗糙度、气流主频及边界层厚度等基本特征进行剖析. 在此基础上，量化分析气体传输率关系建立中存在不确定性的原因，提出更合理的水面气流动力参数，为水面气体传输速率参数选取提供理论依据;探讨气流与风浪的互馈模式，明晰波致气流边界层厚度与风浪间的关系，为有限水域原位监测中确定仪器布设高度提供科学指导.

1 试验设计

1.1 风洞水槽介绍

试验在南京水利科学研究院风洞水槽中开展(图1)，该水槽中已开展了多项有限水域风、浪、流的理论与应用基础研究[18-20]. 水槽有效段长22.5 m，高1.2 m，宽1 m，顶部为弧形盖板(高0.4 m)，进口及出口设置渐变段，边壁为钢化玻璃，底坡为平坡. 风洞进口布置了蜂窝管，以增加气流的紊动程度与均匀性，气流在经过蜂窝管整流后基本为均匀流. 考虑到天然湖泊近岸存在的人工消浪设施或水生植物的消浪功能，水槽尾部设置消浪板. 吸风机设置在风洞尾部，通过橡胶减震片与风洞相连，避免风机震动干扰水体运动. 风洞内可产生最大风速约20 m/s.

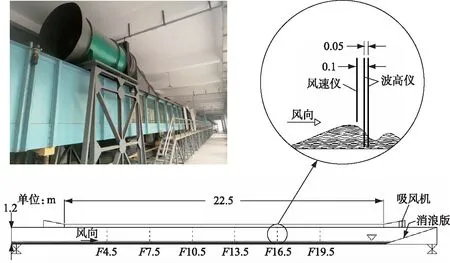
图1 风洞水槽及仪器布设(F4.5～F19.5表征吹程F为4.5～19.5 m)Fig.1 Wind tunnel flume and instrument layout

1.2 数据测量与数据处理

风洞内沿程布置6个测量断面，断面间距3 m. 在每个测量断面中线布设一条风速测线，每个测线沿垂向布置16支热线风速传感器，传感器间距3 cm，采集频率10 Hz，精度1 cm/s，可同步采集水面上方约50 cm高度的瞬时风速. 对应地，在每个测线下风向10 cm处沿风向平行布置2根(1对)电容式波高仪，共计12根，波高仪间距5 cm，采集频率75 Hz，精度1 mm.

风浪主频波长Ld基于1对波高仪同步测量的水面波动，采用互相关分析方法得到[20]；气流与水面波动的频谱图通过快速傅里叶变换(FFT)方法得到，主频为频谱图中能量峰值对应的频率.

1.3 试验方案

本研究为针对有限水域气流演化特征的应用基础研究，试验方案设计在考虑天然水域实际条件的同时，结合研究内容综合考虑. 首先进行无水时(玻璃底壁)气流特征试验研究，而后开展水面气流特征研究. 考虑到湖泊的浅水特征，试验水深d为0.15 m，水温为(18±0.5)℃；共设置7级参考风速(为风洞过风断面的平均风速，由无级变频器精细控制、数字表盘显示)，包含了典型湖泊盛行的风速区间，见表1. 每级风速进行2组试验，试验结果的相对误差均在5%以内，采用2次结果的平均值为最终结果. 根据预试验，风、波、流、雍水等动力现象一般在15 min基本达到稳定，因此，每组试验时长为20 min，最后5 min内对风速与水面波动进行同步采集.

表1 试验组次设计

2 结果分析

2.1 时均风速分布

从半对数坐标系中玻璃壁面条件时均风速分布(图2a)可见，靠近壁面处气流受边壁影响形成气流边界层，同一测线不同高度处风速存在差异，风速随着测点高度的增加逐渐增加并存在风速极大值；图中还绘出了近壁面测点风速的拟合线，发现数据符合对数分布. 采用式(1)可回归得到摩阻风速u*与特征粗糙度z0：

(1)

图2 近玻璃壁面(a)与近水面(b)风速的垂向分布(F=19.5 m)Fig.2 Vertical distribution of wind speed near glass wall (a) and near water surface (b) (F= 19.5 m)

2.2 摩阻风速与特征粗糙度

图3a为两个界面条件下摩阻风速与风速的关系，图中也绘出了Reul等[21]、Liberzon和Shemer[9]与Buckley和Veron[11]水面条件试验结果，其中u10为采用式(1)计算得到的10 m高度处风速[22]. 可见水面条件下试验结果与前人结果较一致；无论是玻璃壁面还是水面条件，摩阻风速与风速均呈正相关，但水面摩阻风速整体大于玻璃壁面条件，小风速时两者差异较小，随着风速的增加，水面条件下摩阻风速随风速的增幅更快，表明水气相互作用后会增加摩阻风速与切应力，即同等风速条件下水气通量传输效率大于玻璃壁面条件下气流与玻璃壁面间的通量传输.

从风速与特征粗糙度的关系(图3b)同样可见，水面特征粗糙度整体大于玻璃壁面条件；玻璃壁面条件下特征粗糙度随风速增加呈现了先增加后趋于平稳的趋势，而水面条件下两者呈正相关，这种差异体现了气-固、气-液的动力作用差异，反映了水气相互作用会增加界面的粗糙程度.

图3 摩阻风速(a)和特征粗糙度(b)与风速的关系Fig.3 Relationship of friction wind speed (a) and characteristic roughness (b) with wind speed

2.3 气流主频与波致气流边界层厚度

从7.7 m/s风速条件下风速能量(S)-频率(f)谱(简称能谱)分布与吹程的关系(图4a)可见，不同吹程下能谱分布无显著差异，且平坦壁面下风速无主频特征. 从10.5 m吹程下风速能谱分布与风速的关系(图4b)可见，能谱曲线谱形随着风速的增加整体上移，表明各频率风速分量均有所增加.

图4 玻璃壁面条件下风速能谱分布与吹程(a)和风速(b)的关系Fig.4 Relationship of wind speed spectrum distribution with blowing fetch (a) and wind speed (b) under glass wall condition

图5为水面条件下风速能谱图. 图5a为10.5 m吹程、12.3 m/s风速条件下，水面上方不同高度处能谱曲线，包括风速全频率能谱图与主频附近的局部能谱图(受风浪与风雍水影响，最低风速测点距时均水面高度为7.5 cm)，由图可见气流受风浪的影响，靠近水面一定区域内存在1.6 Hz的主频，该测点处波致气流边界层厚度δwind介于16.5～19.5 cm之间，主频沿高度方向基本保持不变，越靠近水面主频能量越集中，气流受风浪的影响越显著. 需要说明的是δwind的确定是基于水面上方不同高度处风速能谱是否存在明显主频与能量集中现象，当某一高度的谱形没有主峰时，定义该点高度和相邻下方测点高度的平均值为波致气流边界层厚度，由于两风速测点间距3 cm，因此波致气流边界层厚度数据存在1.5 cm的误差.

图5b为19.5 m吹程、12.3 m/s风速条件下不同高度处风速能谱图，频谱随高度变化规律与图5a相似，但该测点风速主频为1.2 Hz，小于F16.5测点主频(1.6 Hz)，该测点下波致气流边界层厚度介于19.5～22.5 cm之间，大于F16.5测点边界层厚度(16.5～19.5 cm). 表明同等风速条件下随着吹程的增加，近水面气流主频降低而波致气流边界层厚度增加，是有限水域近水面气流沿程演化特征之一.

图5c为19.5 m吹程、7.7 m/s风速条件下不同高度处风速能谱图. 对比图5b可见，相同吹程时(F19.5)，风速由12.3 m/s减低为7.7 m/s后，风速主频1.2 Hz增大至1.77 Hz，波致气流边界层厚度由19.5～22.5 cm降低至12.5～15.5 cm之间. 表明随着风速的减小，近水面气流主频增加而波致气流边界层厚度减小，体现了有限吹程条件下近水面风动力与风速的响应关系，是有限水域近水面气流又一演化特征.

图5 水面条件下风速能谱Fig.5 Wind speed energy spectrum under water surface condition

图6a为近水面风速主频fdwind与风速和吹程的响应关系，黑色数据点为实测值，彩色图为基于实测点的插值结果，由于仪器限制，部分数据缺失，但并不影响对整体趋势的判断，即近水面风速主频随吹程和风速的增加而减小. 从波致气流边界层厚度δwind与风速和吹程的关系(图6b)可见，波致气流边界层厚度与风速和吹程均呈正相关，体现了水面气流边界层内风动力随风吹程及风速增加的演化特征.

过桥汽封位于高、中压缸蒸汽温度最高，启动后温度变化最大的部位。热应力高、膨胀量大，因此在启停阶段热不稳定状态时，造成汽封碰磨的可能性较其他部位大。转子通过一临界时，处于转子中部的过桥汽封部位振幅最大，同样增加了碰磨的几率。布莱登汽封具有机组启动初期可以张开的特点，借此特点可避免出现的上述问题引起的碰磨。因此，布莱登汽封较适用于过桥汽封。高压缸排汽侧平衡活塞直径大，因此漏汽量也较大。漏汽直接流入中压排汽口，为始终保持较低的漏汽量，亦较适合使用布莱登汽封。

图6 气流主频(a)和边界层厚度(b)与风速和吹程的关系Fig.6 Relationship of dominant frequency (a) and boundary layer thickness (b) of airflow with wind speed and blowing distance

3 讨论

湖泊系统涉及水-气和水-泥两个界面，气流是湖泊水体运动的主要驱动力之一，通过影响水体运动强度与模式来营造整个湖泊生态与环境系统. 对湖泊近水面气流特征与水气相互作用开展研究是认识和揭示水气界面物质、能量传递的基础，是物理湖泊学研究的主要内容之一. 然而，由于天然条件的复杂性，难以开展细致、可控的研究. 目前针对水气作用的研究多采用风洞水槽试验的方法，尽管风洞水槽与天然湖泊存在差异，但两个情境下水气相互作用的物理机制是一致的. 相对于野外条件的复杂性，风洞水槽具有的精细可控的优势为水气相互作用系统深入研究提供了有利条件，是天然条件下水气相互作用研究的重要且必要的补充. 下面针对前文水气基本演化特征，从水面气流动力参数的合理选取和气流-风浪互馈模式两方面展开讨论，分析了现有研究存在不足的原因，提出了更加合理的表征水面气流动力强度的参数和波致气流边界层厚度的确定方法.

3.1 水面气流动力参数的合理选取

气流动力条件对湖泊系统影响举足轻重，其中对气流动力参数选取不统一是水气传输速率不统一的主要原因之一. 根据前文试验结果(图2)，在一定的风速、吹程与水深条件下，同一测点处水面上方不同高度处风速存在差异，这就必然导致不同研究者选取风速测点高度时存在不确定性，即同一测点风速具有非唯一性，造成风速-气体传输速率间存在区别. 不少学者根据风速廓线式(1)推算标准的10 m高度处风速u10，并建立u10-气体传输速率间的关系，但这种看似标准化的做法依然存在不妥.

以实测水面上方3 m高度处风速u3为例，根据式(1)计算u10的关系式为(2)，可见式(2)中存在未知量z0，该参数表征了水面粗糙程度，显然该值与气流和水面特征密切相关，也就表明z0在不同风速与测点条件下存在不同(参见图4)，即z0在湖面具有时空异质性. 这就解释了尽管许多学者建立了u10与气体传输速率的关系却依然与其他研究者存在差异的原因.

(2)

基于上述近水面气流特征与演化规律的分析，认为目前以风速作为气流动力参数构建与气体传输速率的关系存在不妥，以摩阻风速或切应力作为气流动力参数更具合理性. 因为它们表征了水气界面作用强度，更具力学意义. 且在一定的水深、吹程与风速条件下，摩阻风速和切应力均具有唯一性，因此，上述两个参数的使用会降低气体传输速率确定的不确定性. 摩阻风速与切应力的获取需要在近水面同时布设两个以上不同高度的风速测点，且两个测点均需在波致气流边界层内(具体波致气流边界层厚度参见3.2节)，而后根据式(1)拟合得到摩阻风速，进一步计算得到切应力.

考虑到天然水域条件的复杂性与不确定性，确实存在不具备测量摩阻风速、切应力的情况. 因此，如能建立z0与风速和吹程的关系，进一步根据式(2)计算得到u10，可避免根据主观经验选取z0带来的不确定性. 在建立关系时为增加所选用数据的代表性，除选用本次试验数据外，数据集中还包括了室内风洞水槽试验，湖泊、海峡等有限水域以及外海3种尺度的数据，所有数据均为实际测量值(表2)，水深d介于0.15～59.00 m之间，风速u10介于5.0～24.4之间，吹程F介于4.5～6100000.0 m之间.

表2 统计数据集

文献[22]指出水气相互作用还会还受到水深影响，因此在探寻z0的关系时考虑了风速、吹程和水深3个因素. 采用非线性回归分析方法，得到了lnz0与u10、F、d的回归关系，见式(3)，相关系数为0.80. 图7为lnz0实测值与根据式(3)得到的计算值的对比，可见不同研究者数据基本分布在45°线两侧，表明关系式(3)的合理性. 由式(3)可见lnz0与风速和吹程正相关，而与水深负相关，即风速和吹程越大，水面粗糙度越大；水深越小，水面粗糙度越大，这一定性结论与文献[22]一致，进一步佐证了式(3)的合理性.

在进行有限水域水面动力参数选取时，可首先确定研究点位的吹程和水深，将其代入式(3)，而后将式(3)代入式(2)，进一步将水面上方z高度处的实测风速uz代入式(2)(代替u3)，最后采用试算法获得u10.

(3)

图7 计算ln z0与实测ln z0的对比Fig.7 Comparison between the calculated ln z0 and the measured ln z0

3.2 气流-风浪互馈模式

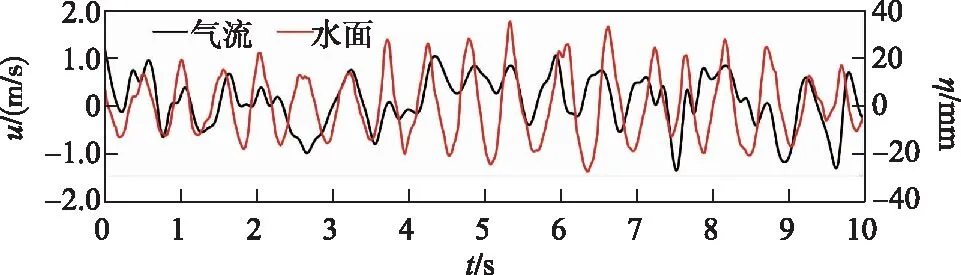
图8 吹程19.5 m、风速7.7 m/s时风速与水面波动的变化过程Fig.8 Change process of wind speed and water surface fluctuation when blowing fetch is 19.5 m and wind speed is 7.7 m/s

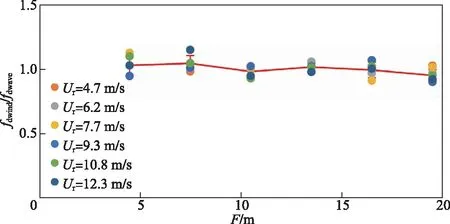
图9 不同风速时fdwind/fdwave与吹程的关系Fig.9 Relationship between fdwind/fdwave and blowing fetch at different wind speeds

气流与风浪相互作用除了体现在“同频率”外，还需考虑风浪直接影响的气流高度，并分析其与风浪尺度的关系，可为水面上方测控设备(如风速仪)布设高度的确定提供指导. 根据实测的波致气流边界层(图6b)及对应主频波高Hd与主频波长Ld(Hd、Ld的计算参考文献[20])，不同风速下δwind/Hd和δwind/Ld随吹程变化见图10，同时绘出各吹程平均值及误差线，结果表明δwind/Hd和δwind/Ld与风速关系不显著，小吹程时δwind/Hd和δwind/Ld均呈增加趋势，吹程大于10.5 m后基本趋于稳定，稳定后δwind约为Hd的3.3倍，约为Ld的0.28倍，与Liberzon和Shemer[9]的试验结果较接近(0.32倍Ld). 但本文在前人基础上，进一步揭示了气流边界层厚度与风浪尺度的关系并非一成不变，而是与吹程呈现一定关系，即在水气作用初期，波致气流边界层厚度增幅较风浪尺度快，当水气作用一段距离后，波致气流边界层厚度增幅与风浪尺度增幅相当，体现了气流与风浪作用的非线性特征.

图10 不同风速下δwind/Hd(a) 和δwind/Ld(b) 与吹程的关系Fig.10 Relationship of δwind/Hd(a) and δwind/Ld(b) with blowing distance at different wind speeds

尽管图10在一定程度上体现了水气互馈过程中的气流边界层发展与风浪特征的关系，但整体而言数据离散程度较大，表明仅采用风浪的某一特征参数难以较全面地体现风浪特征. 考虑到非线性是风浪的重要特征之一，与风浪变形及破碎等现象密切相关，决定了风浪与气流及底壁的能量及物质交换强弱[30]. 因此，考虑采用风浪非线性参数表征风浪特征，并建立其与波致气流边界层厚度的关联. 无量纲数Fc(Fc=g1.25H0.5T2.5/d1.75，H、T分别表示平均波高和波周期)反映了波高、波周期和水深的综合影响，将其作为风浪的非线性特征参数[31]. 不同风速与吹程时风浪的Fc分布见图11(Fc介于2～45之间)，可见随着风速和吹程的增加，Fc值呈非线性增加趋势，吹程及风速较小时Fc增长速率较慢，吹程及风速较大时增幅较快，即风浪的非线性特征随着风速和吹程增加逐渐增强.

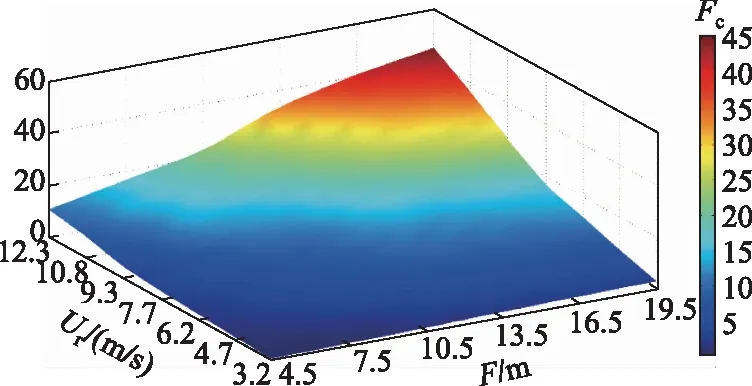
图11 Fc与风速和吹程的关系Fig.11 Relationship of Fc with wind speed and blowing distance

考虑水深对风浪尺度及气流边界层的潜在影响，为使试验结果不失一般性，采用水深d对δwind进行无量纲化，建立无量纲的气流边界层厚度δwind/d，其与风浪非线性参数的关系见图12，可见不同风速时数据点分布较紧凑(显著优于图10)，变化规律较一致，δwind/d随Fc增加呈现非线性增加趋势，在风浪非线性较弱时(Fc较小)增幅较快，随着风浪非线性增强，波致风浪边界层厚度的增幅逐渐放缓，有趋于饱和之势. 由于Fc表征风浪类型，当Fc小于10时风浪为深水波[31]，此时底壁对风浪的约束作用可忽略，水气互馈作用不受底壁影响；而当Fc大于10并逐渐增加时，底壁对风浪的约束逐渐凸显，抑制风浪形态与动力的发展，进一步限制气流边界层发展，表明有限水域中水气互馈作用还会受到水深(底壁)影响. 此外，由图12还可以看出，当Fc大于20时，δwind/d大于1，表明此时波致气流边界层厚度已大于水深.

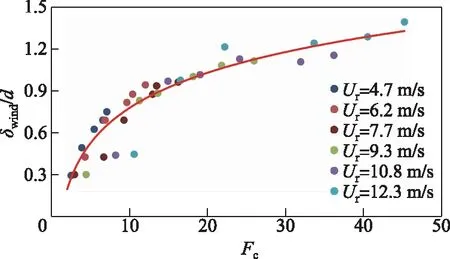
图12 无量纲波致气流边界层厚度与风浪非线性参数的关系Fig.12 Relationship of dimensionless wave and induced airflow boundary layer thickness with wave nonlinear parameters

采用对数函数对数据点拟合得到的关系式(4)，相关系数为0.95. 表明Liberzon和Shemer[9]、Sullivan等[16]、Zavadsky和Shemer[17]等仅采用Ld建立与δwind的关系具有片面性，本文提出采用非线性参数表征风浪特征，综合考虑了波高、波周期与水深等多个因素，在建立其与波致气流边界层厚度间的关系时更具合理性.

δwind/d=0.368 lnFc-0.069

(4)

基于上述波致气流边界层与风浪特征非线性关系的认识，在湖泊水面仪器布设时，应充分考虑当地风浪与水深条件，参考式(4)推算出波致气流边界层厚度，根据仪器功能确定其布设高度，如仪器需要测量水气作用较强烈区域的数据(如近水面风速)，则需将其布设在波致气流边界层内.

4 结论

本文在风洞水槽中模拟研究了有限水域条件下近水面气流演化特征，得到主要结论如下：

1)玻璃壁面与水面条件时近壁面气流均符合对数分布；水面条件下摩阻风速与特征粗糙度均与风速呈正相关，且同等风速条件下均大于光滑壁面时的值.

2)风浪上方一定高度内气流具有主频特征，主频与风速和吹程呈负相关；波致气流边界层厚度与风速和吹程均呈正相关.

3)分析指出了以风速作为气流动力参数构建其与气体传输速率关系存在不妥，阐述了以摩阻风速或切应力作为气流动力参数更具合理性的原因，建立了特征粗糙度与风速、吹程和水深的回归表达式，可为水气界面气体传输效率研究提供参考.

4)近水面气流与风浪具有“同频率”的互馈模式；指出目前普遍采用波长(表征风浪尺度)建立与波致气流边界层厚度的关系具有差异性与片面性，认为采用综合考虑波高、波周期和水深影响的风浪非线性参数Fc建立与波致气流边界层厚度间的关系更具合理性，给出了δwind/d与Fc的经验关系式，可供应用参考.