盾构下穿既有桥梁风险识别及防控方案评价

高文华

（中铁三局集团第四工程有限公司，北京 102300）

随着我国城市建设的不断发展、人口密度的增加和地面交通拥堵已成为制约城市发展的两个主要因素[1-2]。为了解决人口流动集中对交通造成的压力，地下工程建设已成为主要的解决途径。盾构法因其自动化程度高、施工速度快、管理方便、一次性成孔、无气候影响以及对周围环境影响小等优点，已成为地下工程建设的主要施工方法。虽然盾构隧道施工技术具有良好的优势，但在施工过程中针对不同的地质和环境仍不可避免地会造成施工风险[3-6]。此外，轨道交通规划往往是平行于地面交通的主干道，因此地下施工必然要经过大量的桥梁桩基[7]。

城市地下隧道开挖施工，无论开挖的深浅，都将会对地下岩土体产生扰动，打破地层内部原有的应力平衡状态，使其进行应力重分布从而达到一个新的平衡。传统的大城市存在着大量的立交桥、过街天桥、河上部的桥，因此，地铁的修建势必会下穿一些既有桥梁[8]。隧道施工过程中由于桩基打于土体之内，隧道开挖引起土体扰动，使桥梁上部结构出现沉降甚至产生不均匀沉降，当相邻桩基沉降达到一定程度时，会影响桥梁的安全性、耐久性和适用性，严重时可能还会引起失稳破坏。因此，地铁隧道施工对桩基的影响和破坏程度，以及控制和预防方法成为主要的研究问题。

早在1997年同济大学的李永盛等[9]人就提出既有桥梁在盾构施工作用下的主要力学影响是荷载传递和荷载作用，并将弹性地基梁的相关理论运用在盾构施工的桥基上，并结合弹性力学中的Kelvin解推导出了盾构法隧道对既有桩基引起的内力变形公式。杨晓杰等[10]结合广州地铁2号线下穿既有框架建筑桩基础施工工程，应用FLAC3D有限差分软件建模计算，研究表明：隧道施工主要是从桩侧和桩端阻力对桩基承载力产生影响，隧道和桩基之间位置起到关键性因素，不同的位置将产生不同的影响。梁荣柱等[11]在2016年基于Mindlin解并考虑刀盘挤土效应产生的掘进面附加压力、软土地层中具有软化特性且分布不均匀的盾壳侧摩阻力及同步注浆压力引起的地层位移，结合地层损失引起的地层位移，得到盾构施工过程中地表沉降及深层岩土体水平位移的解答。但是，当前的研究主要集中于桥梁所处地基的地质的影响，并没有从桥梁结构本身出发进行研究[12-15]。

基于此，本文首先基于层次分析理论，从不同层次分析盾构隧道下穿既有桥梁保障桥梁稳定性的方案选择，并对不同的方案进行评价分析，通过权重值的排序得出实际施工中的施工方案选择的优劣性，在施工中可以选择合适有效的方法对桥梁的安全运营提供保障。

1 工程概况及区间风险源识别

1.1 工程概况

沈阳地铁九号线怒江公园站-淮河街站区间，起点右线里程DK0+495.903（左线里程DK0+470.900），区间终点里程右DK1+715.275（区间终点里程左DK1+708.869），右线全长1 219.372 m，区间左线全长1 237.969 m。区间在里程DK0+765~DK0+840处下穿新开河，新开河为流经沈阳市的内河，河宽约30 m，西江街以3~12 m空心板梁桥跨越该河，区间右线近距离侧穿桥梁桩基，经现场实际量测，隧道结构与桩基水平最小净距为1.9 m，覆土埋深13.8 m。区间线路在怒江公园出站时线间距为15 m，然后以右线半径R=300 m与左线半径R=500 m的曲线拉开线间距，在西江桥的东西两侧分别下穿新开河，最大线间距约46.5 m。过河后又通过左右线各设置一个半径R=350 m的曲线转至左右线沿淮河街并行，线间距13 m。左右线分别各设置半径R=1 500 m与R=350 m的曲线，将线间距调至17 m，进入淮河街站。

1.2 区间风险源识别

1.2.1 三维程式风险识别

根据盾构施工系统的组成即地质、盾构机、人，将该区间施工风险源分为3大类：自身风险工程、下穿建筑物风险工程、人为因素。将这3个风险结合起来构造出一个三维程式，分别用A、B、C三轴来表示3类风险源[16]。采用集合的形式来对风险源进行说明集合关系，如图1所示。

图1 自身风险工程、下穿建筑物风险工程、人为因素三者关系图

图1中，A={自身风险工程}；B={下穿建筑物风险工程}；C={人为因素}；U={风险源全集}；T={引发事故的风险源}。图1（a）主要表示在施工区间自身存在的风险造成的事故；图1（b）是地铁隧道在区间施工时下穿既有建筑物时所存在的风险造成的事故；图1（c）情况下由于隧道施工本身所存在的风险以及人的操作失误造成事故。在图1（d）情况下由于人没有正确地认识到施工所存在的自身风险以及下穿建筑物的风险工程且没考虑到人的操作失误造成事故。

1.2.2 区间风险源识别步骤及结果

应用三维程式风险识别对该区间的风险源进行识别并划分等级，具体步骤如下。

（1）形成三维网[17]：

a.盾构施工风险有由3部分组成，即图1所示的A、B、C三个部分；

b.每个集合又包含若干次级因素；

c.每个次级因素又包含多个再次及因素。

（2）对各因素进行分析研究：

a.对各个因素进行判断，选出能成为盾构施工的风险源；

b.对图1中的关系进行分析，找出A∩B、A∩C、B∩C共同作用形成的风险源；

c.分析是否存在A∩B∩C共同作用的风险源。

（3）根据识别以及专家意见对风险源进行等级划分，制定出相应的对应措施；

（4）动态施工过程中对风险源进行规避，识别新的风险源。

根据步骤对该区间风险源识别结果见表1。

由表1可知，区间始发接收段、区间联络通道、盾构区间隧道作为自身风险工程属于不可控制和改善的风险源；人行天桥和人工湖作为二级风险源，可以通过施工技术控制和改善；新开河以及上部的西江桥作为该区间工程的一级风险源，必须针对该风险源进行施工影响因素分析。

表1 盾构区间风险源表

由表1可得西江桥作为一级风险源，区间在里程DK0+765~DK0+840处下穿西江桥，西江街主要为空心板梁结构，板宽为3~12 m。盾构隧道右线侧穿桥梁桩基，经现场实际量测，隧道结构与桩基水平最小净距离为1.9 m属于近距离测穿，覆土埋深13.8 m。如图2所示。

图2 区间下穿新开河

2 盾构下穿既有桥梁影响因素权重分析

根据实际的盾构隧道施工现场资料以及相关学者专家的研究成果和现行的施工规范要求，本文建立了如图3所示的层次分析结构图。

图3 层次分析结构图

该层次分析模型主要分为3层，最高目标层即盾构隧道下穿既有桥梁的稳定性保障，更好的保证施工的安全性；中间为准则层，即影响既有桥梁稳定性的主要因素，可以通过对相关因素的控制来保障既有桥梁的稳定性；最下层为方案层，即用来保障既有桥梁稳定性的可供选择的方案。

建立层次分析结构后，将问题分析归结为各种保证盾构隧道下穿既有桥梁稳定性的方案对于实现总目标时选择的优先次序。

2.1 构造判断矩阵

根据层次分析模型，将各层元素进行两两比较，构造出比较判断矩阵。判断矩阵作为层次分析理论的基本信息，也是进行相对重要度计算的主要依据。为了使决策判断定量化，需要将判断矩阵按照一定的比率标度定量化，本文选用1～9标度方法，见表2。

表2 判断矩阵标度及其含义

对于n个元素来说，得到两两比较判断矩阵C=（Cij）n×n其中Cij表示因素i和因素j相对于目标重要值。构造的判断矩阵见表3。

表3 判断矩阵形式

将上述矩阵简写为：

结合层次分析结构和表3的判断矩阵标度，首先得到准则层对于目标层的判断矩阵A-B为：

同理，写出判断矩阵B1（对于隧道施工，为保证桥梁稳定性各方案相对重要性比较）、B2（对于地层变形，为保证桥梁稳定性各方案相对重要性比较）、B3（对于既有桥梁基础本身，为保证桥梁稳定性各方案相对重要性比较），如下所示：

2.2 层次单排序及判断矩阵一致性检验

根据判断矩阵计算对于上一层某元素而言本层次与之联系的元素重要性次序的权值即为层次单排序。本文利用方根法进行层次单排序计算，其计算步骤如下：

判断矩阵的建立将感性的判断思维数学化，将复杂的问题进行定量分析。为了保证专家学者给出的判断指标的协调一致以及不出现相互矛盾的结果，应用层次分析理论要保证判断思维的一致性，故需要对构造的判断矩阵进行一致性检验。

式中：CR为随机一致性比率，当CR<0.10认为判断矩阵具有满意的一致性，否则需要调整判断矩阵；CI作为度量判断矩阵偏离一致性的指标，CI值越大，表明判断矩阵偏离完全一致性的程度越大，反之越小；RI为平均随机一致性指标（当作已知），通过查表4获得相应数值。

表4 平均随机一致性指标

计算某一层次所有因素对于最高层（总目标）相对重要性的权值，称为层次排序。这一过程是从最高层次到最低层次依次进行的。根据计算步骤（1）~（4），首先对准则层对最高层的重要性进行计算，获得权向量（0.623,0.256,0.121）T和最大特征根为3.038。权向量中有3个元素，每一个元素代表的是每一个因素对上一层的因素的权重，最终结果绘制见表5。

表5 准则层判断矩阵数据一览表

表6、表7、表8是方案层对准则层的层次排序计算。计算过程与一致性验证同上，在此不做赘述。

表6 隧道施工（B1）的层次单排序

表7 地层变形（B2）的层次单排序

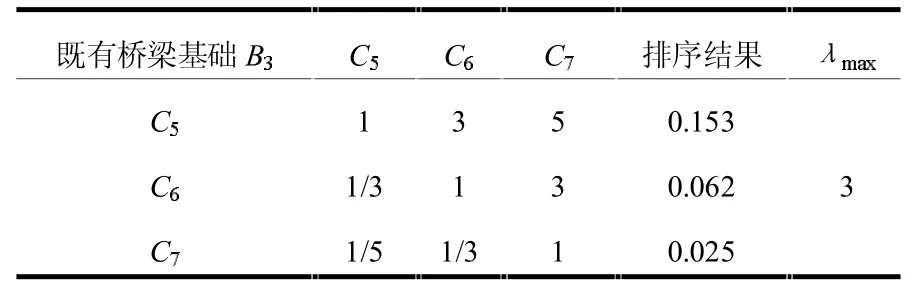
表8 既有桥梁基础（B3）的层次单排序

同理可得，CI=0，RI=0，CR=0<0.10，满足一致性要求。�

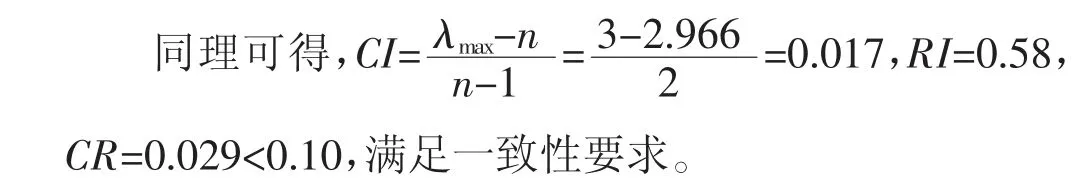
2.3 层次总排序

按照层次结构图，由上而下依次计算得出最低层因素相对于目标层的重要性的排序值。由此可知，层次总排序是针对目标层而言。本文中，各种保障方案对于盾构隧道下穿既有桥梁稳定性这一目的层次总排序见表9。

表9 盾构隧道下穿既有桥梁保障方案总排序

3 保障方案评价分析

通过上述应用层次分析理论计算得出的总排序结果可知，在保证盾构隧道下穿既有桥梁时，按照权重大小来分析，隧道施工对于桥梁稳定性的影响最大，其次为地层变形和桥梁基础本身，针对不同的影响对保障方案进行评价选择[18-20]。本文根据层次结构分析图进行逐层评价分析。

3.1 针对隧道施工的方案评价分析

由表9可得，按照权重大小来分析，隧道施工对于桥梁稳定性的影响最大，而在方案中工法比选和工法优化又是最优先的选择。因此，在隧道下穿既有桥梁时，最重要的是对隧道施工的分析，包括对隧道穿越地区的工程环境、水文地质条件以及隧道的设计要求进行工法比选，选择对地层扰动较小的施工方法。

在确定了施工方法后，就要对工法中包含的主要技术参数进行设定和优化。结合工程隧道所处的环境，采取专家学者的经验以及借助数值模拟的手段可以对隧道下穿造成的施工影响进行预测分析，从而合理选择适用于本工程的施工参数，从而保障桥梁的稳定性。对于盾构法施工参数的选取包括：土仓压力值、盾构掘进顶推力值、掘进速度、出土量、注浆参数的选取、盾构姿态的设定和调整等。

因此工法比选和工法优化是保障盾构下穿既有桥梁稳定性的最主要也是最基础的方案，应该最先考虑[21-22]。

3.2 针对地层变形的方案评价分析

由表7可得，针对地层变形，层次分析结构图中给出了五种方案，其中按照权重分析，注浆加固是所有方案中占比最重要的，其次是地层加固和地层阻隔方案。现将这3种方案进行综合分析评价，评价表见表10。

表10 方案综合分析评价

3.3 针对既有桥梁方案评价分析

由表8中数据分析可得，针对既有桥梁本身给出了3种保障方案，其中注浆加固桥梁基础以绝对的权值优于其它两种方案。因此，本文重点对注浆加固桥桩基础进行分析。

对于既有桥桩的注浆加固一般有两种加固方式，即桩侧注浆和桩端注浆。通过这两种方式的注浆都可以改良桥桩和周边覆土的接触面性质，既可以对地层变形有所帮助又可以提高桩基承载力。两种注浆方式都可以将桥桩本身的承载力充分发挥。但在实际的施工中，要注意既有桥桩加固范围要在盾构隧道施工范围以外，以免对既有桩基产生附加荷载。

由表9计算数据可得，在盾构隧道下穿既有桥梁为了保障既有桥梁的稳定性，可供选择的方案有7种，根据计算得出其相对优劣的排序权值，由权值可以得出以下结论：在保障既有桥梁稳定性的方案中，相对优先顺序为工法的比选和工法的优化、注浆加固、地层加固和地层阻隔以及桩基托换和上部顶升。通过数据的定量判断，施工单位在施工中根据上述评价结果选择实施的先后顺序。

4 结论

本文利用层次分析理论对地铁盾构下穿既有桥梁施工的影响因素以及保障方案进行定性分析，主要结论如下：

（1）在保障隧道下穿既有桥梁方案中，相对优先顺序为工法的比选和工法的优化、注浆加固、地层加固和地层阻隔以及桩基托换和上部顶升；

（2）按照权重大小来分析，隧道施工对于下穿既有西江桥的影响最大，其次为地层变形和桥梁基础本身；

（3）通过计算定量分析，按照权重值分析可得，在实际盾构隧道下穿既有桥梁时，首先应当通过工法比选和优化选定合适的施工方法，设定合适的施工参数，这是保证施工稳定性的最基础也是最重要的环节；其次就是选择注浆加固方式进行安全施工的保障，注浆加固方案是在施工中最优的选择，根据权重值的分析，为以后类似施工的决策者提供借鉴。