基于网络外部性与水平差异化的链与链纵向结构均衡

杨海深

(广东省社会科学院 国际问题研究所， 广东 广州 510610)

一、引言

现代企业的竞争越来越表现为供应链之间的竞争，这种竞争主要表现为多个制造商与专业中间商构成的多节点之间直接或间接的竞争[1]，而供应链内部纵向结构的控制策略成为应对链与链竞争加剧的重要手段。供应链纵向控制结构分为集中决策控制结构(纵向一体化)和分散决策控制结构(分散化)[2]，例如，在PC行业，是以戴尔为龙头构成的制造商—授权专卖店的纵向一体化结构，以及以惠普为龙头构成的制造商—分销商—零售商的分散化结构；在通讯行业，是以中国移动、联通、电信为龙头的运营商—虚拟运营商分散化结构；在手机行业，是以苹果为龙头的授权制造商—零售店的纵向一体化结构，以及以三星为龙头的制造商—代理商—零售商的分散化结构。由于消费市场和竞争环境的演变，供应链纵向结构也在发生变化，那么占据市场主导地位的制造商如何应对来自横向和纵向的竞争压力，决策最优的供应链纵向结构是值得研究的问题。

针对链与链竞争下的纵向结构控制问题，已有较多研究[3-14]。McGuire等[3]研究了两个制造商和两个排他性零售商的竞争结构，主要研究的是商品替代性对纵向结构均衡的影响。研究结果发现，若商品替代性较低，则两个制造商采用集中化结构的分销系统，而如果商品替代性较高，则制造商更可能采用分散化结构的分销系统。Moorthy[4]进一步分析了分散化结构是Nash均衡的原因，即制造商和零售商的战略互动抬升了需求曲线。Trivedi[5]研究了线性需求函数下共用两个零售商的均衡结构，发现零售商和制造商两级层次的竞争均对供应链绩效产生重要影响。Zhao等[6]用不同的服务水平来描述产品差异，发现集中化结构并非是一个均衡结构，而分散化结构才是唯一的Nash均衡。Wu等[7]针对不确定性需求环境，基于库存竞争机制下的报童模型，来研究渠道结构问题，发现当两种商品具有替代性时，集中化结构是唯一的均衡结构。Wu等[8]研究了需求的不确定性、生产成本和商品替代性对渠道结构均衡的影响，发现对于均值固定的均匀分布需求函数，比较高的商品替代性才能保证分散化结构是均衡结构。此外，艾兴政等[9-10]分别基于制造商和零售商讨价还价能力差异，以及从不确定环境下市场风险、预测能力和产品竞争程度来讨论纵向控制结构均衡情况。鲁其辉等[11]考虑了质量和价格竞争下供应链纵向协调均衡问题。廖涛等[12]在价格和服务竞争下研究了服务成本对供应链纵向结构选择的影响。一些学者还研究了影响纵向结构均衡的其他因素，比如，成本差异与产品替代组合[13]，以及价格竞争下规模不经济成本[14]对供应链纵向控制结构选择绩效的影响。

综合以上文献可以发现，目前的研究大多基于产品价格竞争机制，仅有少数学者基于价格和服务竞争(如Zhao等[6]、廖涛等[12])来研究供应链纵向结构均衡问题，并且这些研究也只关注了受价格和服务水平影响的需求函数。本文将基于Hotelling模型，从消费者效用函数出发，建立受价格、服务水平和商品水平差异化影响的市场需求函数，在价格和服务水平竞争的情形下，研究商品水平差异化对供应链纵向结构均衡的影响。

同时，网络经济时代的供应链系统和节点企业深受网络外部性的影响。网络外部性概念最早由Katz等[15]于1985年提出，并将其定义为单个消费者的效用随着购买相同或兼容产品的总人数增加而提高，典型的商品有手机、电脑和传真设备等。网络外部性对企业的影响体现在：一是只有网络规模达到一定临界值时，市场才能形成；二是“赢家通吃”或“输家通盘”的现象加剧市场竞争，对企业决策产生重要的影响。随后，国内外学者开展了广泛的研究，主要集中在带有网络外部性的商品最优定价策略[16-19]、商品最优研发策略[20]、最优技术兼容性决策[21-23]等几方面。特别地，Liu等[24]研究了网络外部性影响下的消费者效用函数，用来反映消费者由于存在网络外部性而增加的购买意愿，并进一步分析了网络外部性对销售渠道选择的影响。但是，以往研究未考虑网络外部性对链与链竞争下纵向结构选择的问题。事实上，如Katz等[15]所述，网络外部性会通过影响消费者预期来影响其购买决策，而零售商也不得不考虑消费者预期所带来的市场需求的影响，并在此基础上制定新的价格和服务水平，并且由于零售商的杠杆效应，这种影响势必会沿着供应链向上游传递，造成上游制造商的生产和定价等决策的变化。因此，网络外部性的存在，将会极大地影响到整个供应链系统,有可能会加剧或者缓解供应链不同纵向控制结构间的绩效损失，直至影响链与链之间的纵向结构均衡。鉴于此，本文基于价格和服务水平竞争，构建基于网络外部性和水平差异化的链与链纵向结构博弈模型，探讨网络外部性和水平差异化作用下的纵向结构均衡条件，以及其对供应链纵向结构均衡的影响。

二、基本模型

本文研究的供应链系统由两个制造商和两个排他性零售商组成的链1和链2构成(见图1)，并且它们之间遵循基于价格和服务水平竞争的博弈规则。在每条链上制造商以批发价向零售商出售商品，零售商以零售价售卖商品并向消费者提供相应的销售服务，两条链之间进行价格和服务水平竞争。制造商决定批发价，零售商决定商品价格和服务水平，并且假设制造商和零售商是完全理性及风险中性的决策者，以利润最大化作为其决策目标。

图1 竞争供应链结构

(一)需求函数

(1)

(二)利润函数

因为制造商的单位生产成本和零售商的边际销售成本对模型结果不产生本质影响，为方便分析，不妨假设它们均为零。因此，供应链i制造商的利润函数为：

(2)

为了更好地凸显网络外部性对供应链纵向结构的影响，这里假设两个零售商的服务效率和服务能力相当，即有相同的服务成本系数η。因此，零售商利润函数为：

(3)

因此，整个供应链的利润函数为：

(4)

要保证式(2)、式(3)和式(4)利润函数最优值存在和均衡结果有意义，这里做一技术性假设：

2t-δ1-δ2>θ2/η

(Ⅰ)

三、模型求解

本文采用完全信息下的静态博弈模型来刻画链与链之间基于价格和服务水平竞争的博弈行为。单条链内部如果是分散化决策结构，则表示存在着垂直竞争，可以用制造商主导的斯坦伯格博弈来刻画。因此，我们构建四种不同纵向结构下的博弈模型：链1与链2均为集中化决策结构；链1为集中化决策结构，链2为分散化决策结构；链1为分散化决策结构，链2为集中化决策结构；链1与链2均分散化决策结构，分别记为CC模型、CD模型、DC模型和DD模型。

(一)CC模型

在两条链均为集中化决策结构的情况下，充分合作的制造商和零售商通过联合决策使整条供应链的利润最大化，在两条链之间水平竞争条件下，最终获得各自的最优商品销售价和服务水平。

集中化决策结构下每条供应链的利润函数为：

(5)

由式(5)关于pi,si的一阶条件可得：

因此，得到每条链的最优价格和服务水平为：

(6)

其中，记A=2t-δ1-δ2，记B=3ηA-2θ2，记Ci=η(3t-δi-2δj)-θ2。进一步，可得每条链的均衡需求、均衡利润和竞争区域，如表1所示。

(二)CD模型

若供应链1为集中化决策结构，供应链2是以制造商为主导的分散化决策结构，那么博弈顺序为：(1)两条链首先进行水平竞争；(2)链1对商品销售价格和服务水平进行独立的集中化决策，同时链2制造商先行决定批发价，零售商再决定商品销售价格和服务水平。可以采用逆向归纳法来求解。

首先，供应链1进行集中化决策，则它对供应链2的反应函数可以由上述CC模型的结果得到，即：

其中，D=2ηA-θ2。

供应链2零售商利润函数为：

则由零售商关于p2,s2的一阶条件，得到零售商的反应函数为：

因此，供应链2制造商决策模型为：

求解上式，便能得到供应链2对供应链1的批发价、销售价和服务水平的反应函数分别为：

其中，记E=3ηA-θ2。

在链与链之间同时进行水平竞争的情形下，便得到均衡下的每条链的最优价格和服务水平：

(7)

其中，记F=5ηA-3θ2，记G1=η(7t-3δ1-4δ2)-2θ2。进一步，可得每条链的均衡需求、均衡利润和竞争区域，如表1所示。

由于结构的对称关系，同理可求得DC模型的结果，如表1所示。

(三)DD模型

若两条链均以制造商为主导的分散化决策结构，那么博弈顺序为：(1)两条链首先进行价格和服务水平竞争；(2)链1和链2的制造商分别独立先行决定批发价，零售商再决定商品销售价格和服务水平。可以采用逆向归纳法来求解。

两条供应链零售商利润函数为：

则得到零售商的反应函数为：

同样容易验证，零售商利润函数关于pi,si的海塞矩阵在条件(Ⅰ)是负定的，即利润函数关于pi,si存在最大值。

两条供应链制造商的决策模型为：

求解此模型，便得到以制造商为主导的供应链j对供应链i的批发价、销售价和服务水平反应函数分别为：

在链与链之间同时进行水平竞争的情形下，可以得到均衡下的每条链的最优价格和服务水平分别为：

(8)

其中，记H=7ηA-4θ2，记Gi=η(7t-3δi-4δj)-2θ2。进一步，可求得每一条链的均衡需求、均衡利润和竞争区域，如表1所示。

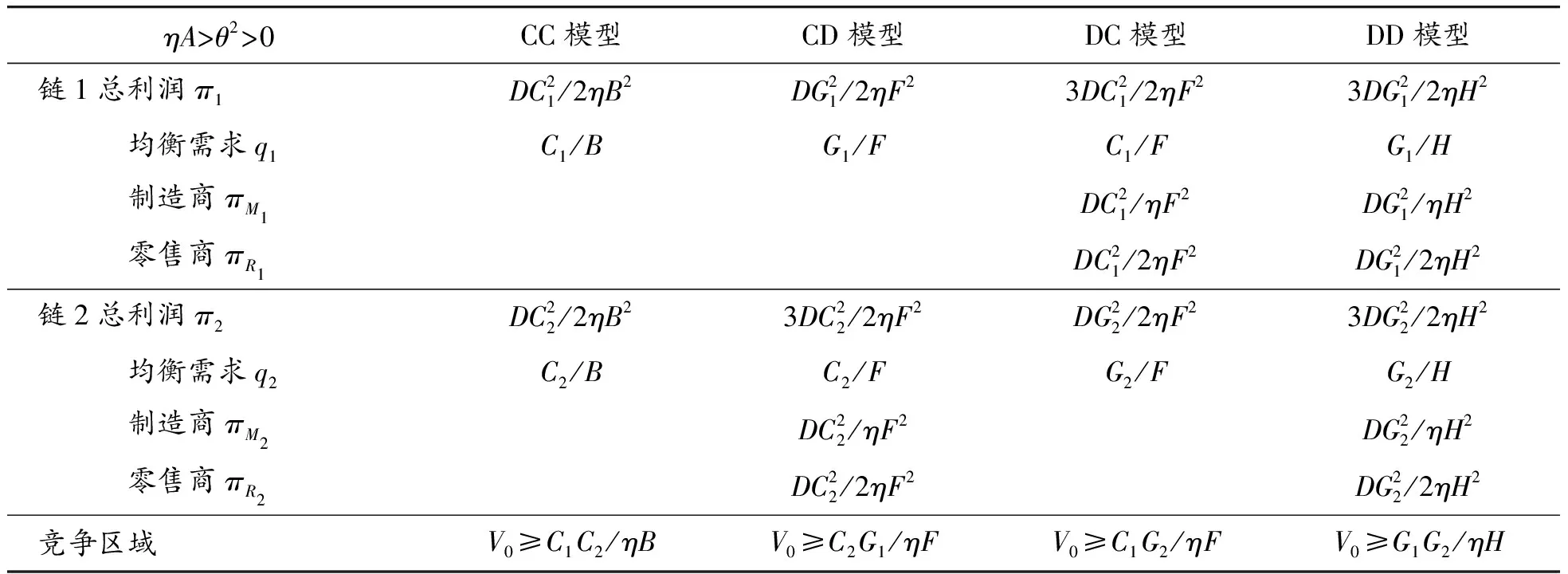
表1 链1和链2的均衡值汇总

四、博弈均衡分析

本节将依据表1的结果，构建链与链之间的纵向结构博弈模型，即把链1和链2作为博弈参与人，把供应链集中化决策和分散化决策作为博弈策略，在完全信息并且同时决策情况下，两个参与人的支付矩阵如表2所示。接下来，我们将探讨纵向结构博弈模型的Nash均衡问题，以及侧重分析商品网络外部性和水平差异化对Nash均衡的影响。

表2 支付矩阵

在两种产品的网络外部性强度存在差异时，不妨假设δ1>δ2，着重考察网络外部性强度的差异Δδ和水平差异化程度t对链与链纵向结构均衡的影响。

命题1对于链1来说，

命题1中的(1)表明：当两条链所供应商品的网络外部性强度差距较大，并且商品的水平差异化程度不是太大(t≤t1)时，链1在集中—集中(C,C)策略下的绩效要优于在分散—分散(D,D)策略下的绩效。命题1中的(2)表明：在网络外部性强度差距较小时，或者网络外部性强度差距较大，同时产品的水平差异化程度也较大时，链1在(D,D)策略下的绩效要优于在(C,C)策略下的绩效。

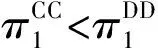
推论1说明，对于两种商品的网络外部性强度差距非常小时，链1在(D,D)策略下的绩效要优于在(C,C)策略下的绩效。

命题2

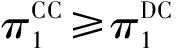
命题2中的(1)表明：在商品的水平差异程度不太大(t≤t2)时，在链2选择集中化决策的情况下，链1的最优选择是集中化决策；在链1选择集中化决策情况下，链2的最优选择是集中化决策。反之，当商品的水平差异程度较大时，命题2中的(2)的结果表明：在链2选择集中化决策的情况下，链1的最优选择是分散化决策；在链1选择集中化决策情况下，链2的最优选择是分散化决策。网络外部性强度差异大小对命题2的结论没有影响，因此当δ1=δ2时，命题2依然成立。

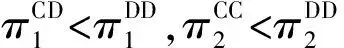
命题3表明：无论商品网络外部性强度的差异大小，还是水平差异化的程度高低，在链2采取分散化决策时，链1的最优策略总是分散化决策策略；在链1采取分散化决策时，链2的最优决策是分散化决策；链2在(D,D)策略和(C,C)策略中，总是倾向于选择前者。

命题4

(3)其他情况下，纵向结构Nash均衡于(D,D)纯策略。

命题4表明：在两条链所供应的商品的网络外部性强度差距较大，且商品的水平差异化程度不是太大(t≤min{t1,t2})时，链与链之间竞争结构的最优选择策略都是(C,C)和(D,D)纯策略；而在网络外部性强度差距较小，或者商品的水平差异较大时，链与链之间竞争结构的最优选择策略是(D,D)纯策略。

推论2当两种商品的网络外部性无差异时，即δ1=δ2时，有以下结论：

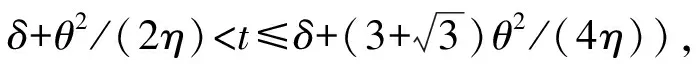
综合上述命题和推论的结果可知，如果消费者市场需求受商品的网络外部性、商品间的水平差异化、零售价格和服务水平影响，并且由制造商主导的两条链之间进行价格和服务水平竞争，具备同等的服务能力，那么只有当两种商品的网络外部性强度差异较大，并且水平差异化程度不太大时，两条供应链的纵向最优控制结构才可能均为集中化(一体化)决策，即(C,C)策略；而在其他情况下，纵向最优结构总为分散化决策结构，即(D,D)策略，并且分散化决策结构在特定条件下还是帕累托最优结构；此外，两条链本身不存在混合结构的均衡。结论中一些点与现实中的受上述因素影响的供应链纵向结构决策结果相一致，比如在智能手机产品上，小米手机起初凭借论坛、发布会、微博等新媒体进行口碑宣传和“高配置、低价格”定价策略，产生出高于其他同类产品较大的网络外部性效应，这也决定了其销售策略为自建的官方商城，即采用集中化决策策略；但随着其他手机品牌的崛起和消费者偏好转移，小米手机的网络外部性强度差距变小，其销售渠道也变得更加多元化，此时更倾向选择分散化决策策略。

五、算例分析

下面通过算例对第4节结论作进一步验证和分析，这里不失一般性，假定消费者对服务质量的敏感系数θ=0.2，那么零售商提供相应服务的成本系数η=0.7。在两种产品的网络外部性强度存在差异时，分别考虑两种商品网络外部性强度差异Δδ和水平差异化t的变化对供应链绩效的影响，分别做出链1和链2不同策略下的收益关于Δδ和t的对比图，以及由Δδ和t共同决定的纵向结构均衡区域图。

首先，当水平差异化t固定(假定t=0.6)时，考虑网络外部性强度差异Δδ变动对不同纵向结构下链1和链2绩效的影响。根据条件(I)和δ2<δ1，假定δ2=0.1，则Δδ=δ1-δ2=δ1-0.1，在(0.1，0.9)区间内取值，分别作出CC模型、CD模型、DC模型和DD模型下的链1和链2总利润对比图，如图1所示。

其次，在网络外部性强度差异Δδ固定时，设定Δδ=0.8，考虑水平差异化t变动对4种纵向结构下链1和链2绩效的影响。根据条件(I)，t>0.54，分别作出CC模型、CD模型、DC模型和DD模型下的链1和链2总利润对比图，如图2所示。

图2 t变动时不同结构下链1和链2绩效对比

最后，图3给出了由Δδ和t共同决定的纵向结构均衡区域，图3中区域(1)对应的纵向结构Nash均衡于(C,C)和(D,D)纯策略的区域，此时，两种商品的网络外部性强度差异较大，且水平差异化程度不太大；图3中区域(2)对应的是纵向结构Nash均衡于(C,C)和(D,D)纯策略，并且(D,D)是帕累托最优区域，此时，两种商品的网络外部性强度差异较小，且水平差异化程度不太大；区域(3)对应的是(D,D)纯策略区域，此时，商品的水平差异化较大。

当两种商品的网络外部性强度无差异时，图4给出了由δ和t共同决定的纵向结构均衡区域，图4中区域(1)对应的纵向结构Nash均衡于(C,C)和(D,D)纯策略区域；图4中区域(2)对应的是(D,D)纯策略区域。

图3 由Δδ和t确定的纵向结构均衡区域

六、结论

在网络外部性环境下，构建了由两个制造商和两个排他性零售商组成并进行价格和服务水平竞争的供应链系统。首先，在集中—集中决策、集中—分散决策、分散—集中决策和分散—分散四种决策模式下，分析和探讨了节点链和企业的商品定价、服务水平决策以及系统利润，然后，构建了由两条链作为参与人的供应链纵向结构博弈模型，接着分析了纵向结构的博弈均衡问题，以及网络外部性和水平差异化对博弈均衡结构的影响，最后通过算例作进一步的分析，得到以下结论：

(1)两种商品的网络外部性强度差异和水平差异化对两条链纵向均衡结构产生重要的影响。较大的网络外部性差异，或者较小的水平差异化程度使得两条链纵向结构均衡于集中—集中策略和分散—分散策略，并且商品的网络外部性强度大的一方更加倾向于集中—集中策略；较小的网络外部性差异，或者较大的水平差异化使得两条链纵向结构均衡于分散—分散策略。

(2)对于同等网络外部性强度的两种商品而言，只要商品的网络外部性，或者水平差异化保持在适度的区间，两条链纵向结构决策的Nash均衡为集中—集中策略和分散—分散策略，并且分散—分散策略是帕累托最优策略；但是当网络外部性强度较小，或者水平差异化较大时，两条链纵向结构均衡于分散—分散策略。

本文尚有不足之处，例如考虑的需求函数有些特殊，未考虑不确定性需求、服务成本差异等对供应链纵向结构均衡的影响，这些都是可以拓展的方向，需要进一步研究。