Phase-matching quantum key distribution with light source monitoring
Wen-Ting Li(李文婷) Le Wang(王乐) Wei Li(李威) and Sheng-Mei Zhao(赵生妹)
1Institute of Signal Processing Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
2Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Ministry of Education,Nanjing 210003,China
Keywords: phase-matching quantum key distribution,source fluctuation,light source monitoring
1. Introduction
Quantum key distribution (QKD) is the most successful application in quantum information science, and its security has been proved at the end of the last century.[1–3]It enables distant parties to achieve the secure key by harnessing the laws of quantum mechanics.[4,5]After the first QKD protocol was proposed in 1984,[4]QKD has made great progress in theory and practice,such as decoy-state QKD protocol,[6,7]measurement-device-independent (MDI) protocol,[8,9]and round-robin differential-phase-shift (RRDPS) protocol.[10,11]Usually, photons are used as information carriers in QKD’s implementations. However, the transmission loss of photons has become a major obstacle in practical applications, resulting in the linear key-rate bound (PLOB bound) for QKD system.[12]In fiber-based networks, the transmission rate(η)decreases exponentially with the communication distance,which limits the transmission distance of the practical QKD system.
Marvelously,a quantum key distribution protocol,named twin field quantum key distribution (TF-QKD) protocol, was proposed in 2018[13]to surpass the PLOB bound[12]and make a quadratic improvement over phase-encoding MDI-QKD protocol.[14]It has attracted much attention recently.[15–21]For TF-QKD protocol,the security problem caused by phase randomization was its main disadvantage. And phase matching quantum key distribution (PM-QKD) protocol[22]was then proposed to resolve the security loophole by adding an extra test mode. PM-QKD protocol could not only exceed the linear key rate limit, but also resist all probe attacks due to the independence of the measurement device. Recently,Maet al.[23]have proposed the reference-frame-independent design for PM-QKD protocol,which can well solve the performance degradation of reference system caused by offset. However,the quantum state prepared at the source was assumed to be an ideal coherent state in the original PM-QKD protocol. Actually, this assumption is not guaranteed in practice, leading to practical secure issues.[24]In addition, there also exists a non-ideal source problem causing the photon number distribution(PND)of the light source to be unknown and the prepared state to no longer be an ideal coherent state.
On the other hand, light source monitoring (LSM) was proposed to solve the non-ideal source problem by monitoring the photon number distribution (PND) of the non-ideal light source.[25]The monitored statistical parameters can then be used to recalibrate the PND of the light source to estimate the final secret key rate, resulting that the assumption of ideal source is not necessary in QKD process. LSM was successfully applied to MDI-QKD protocol to solve the nonideal source problem theoretically based on the “untagged bits”concept,[26]and then based on a photon number resolving(PNR).[27]LSM was also used for the sending-or-not-sending(SNS)protocol to demonstrate that the security of SNS protocol is still valid under a source with unknown PND.[28]
In the paper, we propose a PM-QKD with light source monitoring protocol, named PM-QKD-LSM protocol. In the protocol,the non-ideal light source is used to generate the light beam by Alice and Bob independently. After phase and intensity modulation, the light beam is then split to two paths by a beam splitter (BS), where one is input to the LSM module to estimate the probabilities that the light pulse signals contain zero photon, one photon, or two photons, and the other is emitted to the measurement site,Charlie,for detection. By matching phases with each other during post-selection,the key information is encoded into the common phase, and then the key can be obtained through the success detection results.
The advantages of the proposed PM-QKD-LSM protocol are:(1)it overcomes the problem of non-ideal light source and improves the security of the PM-QKD protocol;(2)its performance under the unknown PND condition (UPC) can almost keep the same as that of PM-QKD protocol under ideal source condition without source fluctuation; (3) it is more independent of the source fluctuation than the PM-QKD protocol;and(4)the performance is almost unchanged as that of PM-QKD protocol under asymmetric channel.
The contribution of this paper is that we investigate the ability of LSM in solving the non-ideal light source problem in PM-QKD protocol,and discuss the performance of PM-QKDLSM protocol under different source fluctuation.Furthermore,we enrich the work on the performance of PM-QKD-LSM protocol with symmetrical or asymmetrical channel. The results are helpful for the design of the practical PM-QKD system.In addition,the results in the paper show that the protocol we proposed not only solves the problem of non-ideal light source at the light source side,which relaxes the requirements on the light source, but also improves the security of the PM-QKD protocol. The improvement can be addressed from the following two aspects. One is that the LSM module itself has the function of monitoring the probability of the number of photons in our proposed protocol, which can detect the PNS attack. The other one is that the LSM module can also be regarded as a monitoring unit to monitoring the arrival time of the pulses so as to resist the phase-remapping attack.
The paper is organized as follows. In Section 2, we first present the PM-QKD-LSM protocol, then we use the LSM method to obtain the tight bounds of the parameters for the secret key rate, and discuss the performance of the proposed protocol under the source fluctuation. In Section 3,we present some numerical analysis results. Finally,we draw the conclusions in Section 4.
2. PM-QKD-LSM protocol
2.1. The protocol
The schematic diagram of PM-QKD-LSM protocol is shown in Fig. 1, where the two communication parties, Alice and Bob,generate her(his)coherent state pulses,independently at first. Before sending their coherent state pulses to an untrusted measurement site,Charlie,Alice and Bob use a LSM module individually to estimate the tight bound of the photon number probabilities (PnL(μk),PnU(μk)) on her(his) PND of the light source. Here, the subscribe L (U) andndenote the lower(upper)bound and the photon number(n=0,1,2), respectively. Then, Charlie is expected to perform the interference detection. This interference measurement would match the phases of Alice and Bob’s signals. Conditioned on Charlie’s announcement,there is a correlation between the key information of Alice and Bob.
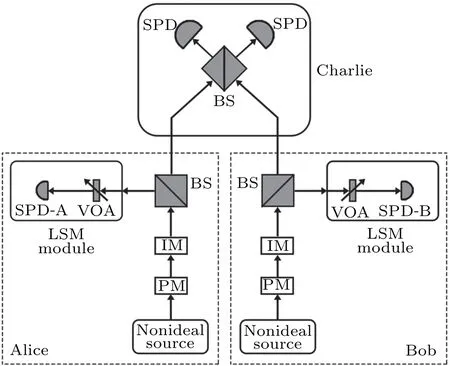
Fig.1. The schematic diagram of PM-QKD-LSM protocol. SPD,a single photon detector; VOA, a variable optical attenuator; BS, the beam splitter; IM, intensity modulator; PM, phase modulator. The LSM module consists of a variable optical attenuator and a single photon detector(SPD-A/SPD-B).
The proposed protocol can be described in detail as follows.

(ii) Measurement Alice and Bob use the beam splitter(BS) to split the light beam into two paths. One is used for LSM module to estimate the photon number probabilities and the other is sent to the measurement site(Charlie)with transmittancesηa(ηb). By changing the attenuation coefficient(ηi)of the VOA in the LSM module,Alice(Bob)measures the probabilities(Pμk(ηi))that the SPD-A(SPD-B)not responds.Charlie is expected to perform the interference detection and record which detector(right detector or left detector)clicks. A successful detection is defined as that one and only one of the two detectors clicks,denoted byL-click andR-click.


(vi) Key generation Alice and Bob repeat steps (i)–(v)until they have enough sifted keys. Afterwards, they perform an error correction and privacy amplification on the sifted key bits to get a fully secret key.
2.2. The security analysis
In this section,we discuss the security of PM-QKD-LSM protocol.
As discussed above, PM-QKD-LSM protocol also includes state preparation,measurement,announcement,sifting,parameter estimation and key generation. The first difference between PM-QKD-LSM protocol and original PM-QKD protocol is the state preparation step. In original PM-QKD protocol,Alice(Bob)prepares the coherent state pulse and encodes the key information into the phases of the coherent states. It is assumed that the light source at Alice (Bob) side is a coherent state source with a average photon number which satisfies the Poisson distribution. However, the photon number distribution is unstable in the proposed PM-QKD-LSM protocol due to the non-ideal factors of the light source. Therefore, LSM module is adopted by Alice (Bob) to estimate the photon number probabilities. Obviously, the usage of LSM module does not affect the sooner measurement step, the following announcement and sifting. The second difference is the parameter estimation step, PM-QKD-LSM protocol adds the probability estimations of zero photon, one photon, and two photons precisely, which only has the relationship with the secure key rate, and is discussed in the following subsection. Hence,we only prove that the quantum state prepared in our protocol does not introduce the security problem.



Hence,it is shown that the quantum state is formally consistent with that of PM-QKD protocol. Moreover,the security proof of PM-QKD protocol[22]can be fully applied to our proposed protocol.
For the actual system security, the structure of system may introduce some security vulnerabilities. We discuss the security of the proposed protocol against the security vulnerabilities,individually,as follows.
(i)PNS attack During the proposed protocol,the eavesdropper(Eve)has the chances to intervene and eavesdrop the signal by beam splitting attack(PNS).As PM-QKD protocol,we use the decoy state method in the proposed protocol,that is effectively against PNS attack. In addition, the LSM module used in the proposed protocol can estimate the probabilities of zero photon, single photon and two photon precisely, so that the PNS attack can be detected by Alice(Bob),and the security can be improved.
(ii)Phase-remapping attack Ideally,the pulses undergo a phase modulation by the phase modulator.If Eve can change the arrival time of the pulses,then the pulses will pass through the phase modulator at different time, resulting in different encoded phases. This phase remapping process allows Eve to launch an intercept-and-resend attack. However, the LSM module can also be approximately regarded as a monitoring unit to monitor the arrival time of the pulses so as to resist this attack.
(iii) Other practical issues A single photon detector(SPD),together with a variable attenuator,are used in our proposed protocol. The SPD may have a high dark count rate(DCR) when it works at room temperature, which may increase the time of monitoring the results. A high DCR and the increased monitoring time can introduce the overestimation of secret key rate. However,the SPD is set near the light source in our protocol and DCR=10-8≪1(in our simulations),[25]which make the increased monitoring time ignored.Of course,the DCR of SPD may fluctuate in the actual environment,and other parameters,such as the detection efficiency of SPD,may drift. One can calibrate all parameters of the monitor in real time,[25]or present a range of parameter drifts and give a reasonable estimation of the lower bound of secret key rate (R)with the worst cases within the fluctuation range.
2.3. Secret key rate of the protocol
In PM-QKD-LSM protocol, three different coefficients(η0,η1andη2)are used to concisely estimate the photon number probabilities(PnL(μk),PnU(μk)),and they are controllable.The relation[29]betweenPμk(ηi)andPn(μk)can be described as




2.4. Source fluctuation
For a real-life QKD system,the PND of the light source’s signal is not fixed, that is, there is a problem of the light source fluctuation. Importantly, the performance of the PMQKD protocol is greatly degraded in this condition.Therefore,we further discuss the intensity fluctuation for PM-QKD-LSM protocol.
Specifically, the signal emitted from the light source can be considered as a fluctuated coherent state which has an average photon number with Gaussian-distribution.[27,28]In PMQKD-LSM protocol, the signal after attenuation still has a Gaussian-distribution average photon numberμ, which has a probability distribution of
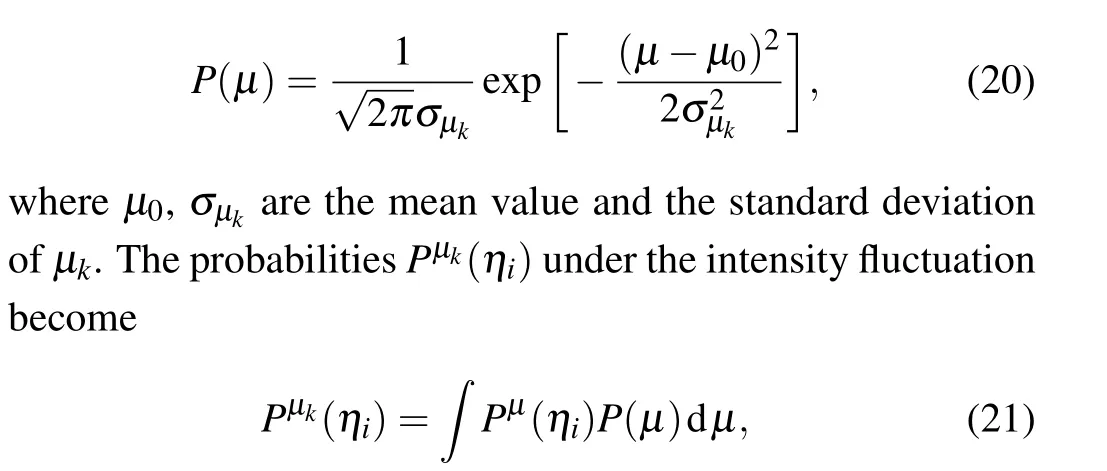
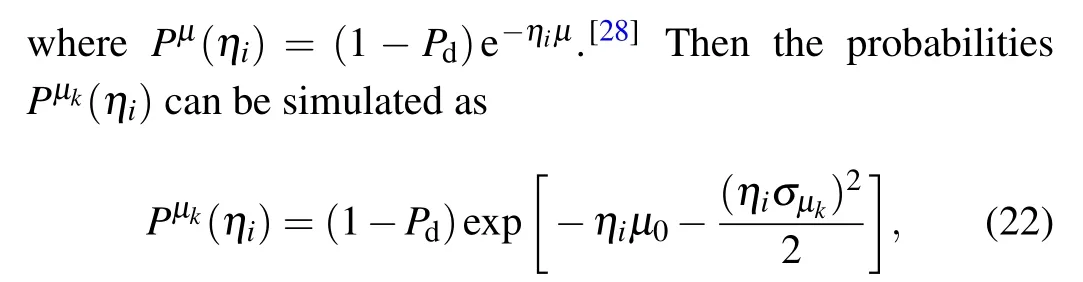
whereσμk=σμ0,σis the fluctuation coefficient. With Eqs. (4)–(9), thePn(μk) can be estimated byPμk(ηi) under considering the source fluctuation.[31,32]
3. Results with numerical simulation


Table 1. Estimation result of{PnL(μk),PnU(μk)}in the LSM scheme.
Then,we discuss the performance of the proposed protocol. The parameters are the same as those in Ref.[30],which are listed in Table 2.
Figure 2 shows the secret key generation rate of the proposed protocol against transmission distance, together with that of original PM-QKD protocol. The results show that PM-QKD-LSM protocol can exceed PLOB bound when the transmission distance is greater than 212 km, and the performance of PM-QKD-LSM protocol (dashed curve) is close to that of the original PM-QKD protocol(solid curve).The ratios of secret key rate between PM-QKD-LSM protocol and PMQKD protocol are about 93.6%,93.0%,92.4%at the distance of 100 km, 200 km, 400 km, and the maximum transmission distances of PM-QKD-LSM protocol and PM-QKD protocol are 504 km and 507 km, respectively, where the maximum transmission distance is calculated asL=LA+LB.
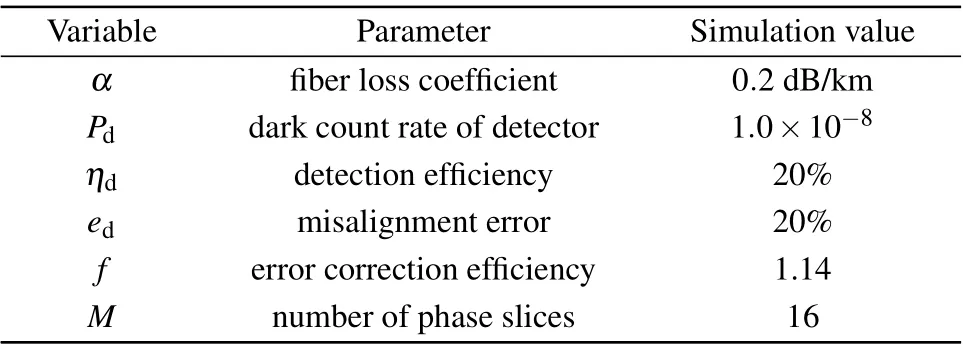
Table 2. The numerical simulation parameters.

Fig. 2. The performance of PM-QKD-LSM protocol in comparison with that of PM-QKD protocol with the parameters set in Table 2. For 300 km transmission distance, the secret key rate for PM-QKD-LSM protocol is 2.23×10-6,while it is 2.41×10-6 for PM-QKD protocol.

Fig. 3. The performance of the PM-QKD-LSM protocol with a nonideal and fluctuated light source compared to the PM-QKD protocol.σ: the fluctuation coefficient. For the PM-QKD-LSM protocol,a small fluctuation σ=1%(solid curve)and a large fluctuation σ=10%(dashdotted curve)are considered.For the PM-QKD protocol,a small fluctuation σ =1%(dashed curve)and a relatively large fluctuation σ =2%(dotted curve)are considered.
After that,we discuss the performance of both PM-QKD protocol and PM-QKD-LSM protocol under the different fluctuation coefficientσ=σμk/μ0in Fig. 3. The values of intensities for the PM-QKD-LSM protocol and the PM-QKD protocol are optimized, and other simulation parameters are set the same as Table 2. It is shown that the PM-QKD-LSM protocol performs well in the practical systems. For the different fluctuation coefficientσ, the PM-QKD protocol has a obviously weaker performance, as its maximum transmission distance decreases to about 480 km for a small fluctuated light source(σ=1%),then decreases to about 460 km whenσup to 2%. However, for the PM-QKD-LSM protocol, its performances are almost unchanged under the fluctuated condition fromσ=1%toσ=10%.

The above discussions are under the symmetric condition which satisfyLA=LB. Later, we discuss the performance of PM-QKD-LSM protocol under the asymmetric channel.Hence, we set the transmission distance to satisfyLB-LA=30 km andμA,μB ∈{0,μ/2,ν1/2},whereμ/2 is the signal intensity. Other simulation parameters are set the same as those in Table 2. Figure 5 shows the performance of the PM-QKDLSM protocol and the PM-QKD protocol under the asymmetric channel without source fluctuation,where the transmission distanceL=LB+LA. The results show that PM-QKD-LSM protocol can exceed PLOB bound when the transmission distance is greater than 275 km. The performance of PM-QKDLSM protocol (dashed curve) is almost same to that of PMQKD protocol (solid curve) for all the transmission distance.For 300 km transmission distance,the secret key rate for PMQKD-LSM protocol is 5.13×10-7,while it is 5.70×10-7for PM-QKD protocol,they are smaller than those under symmetric channel.
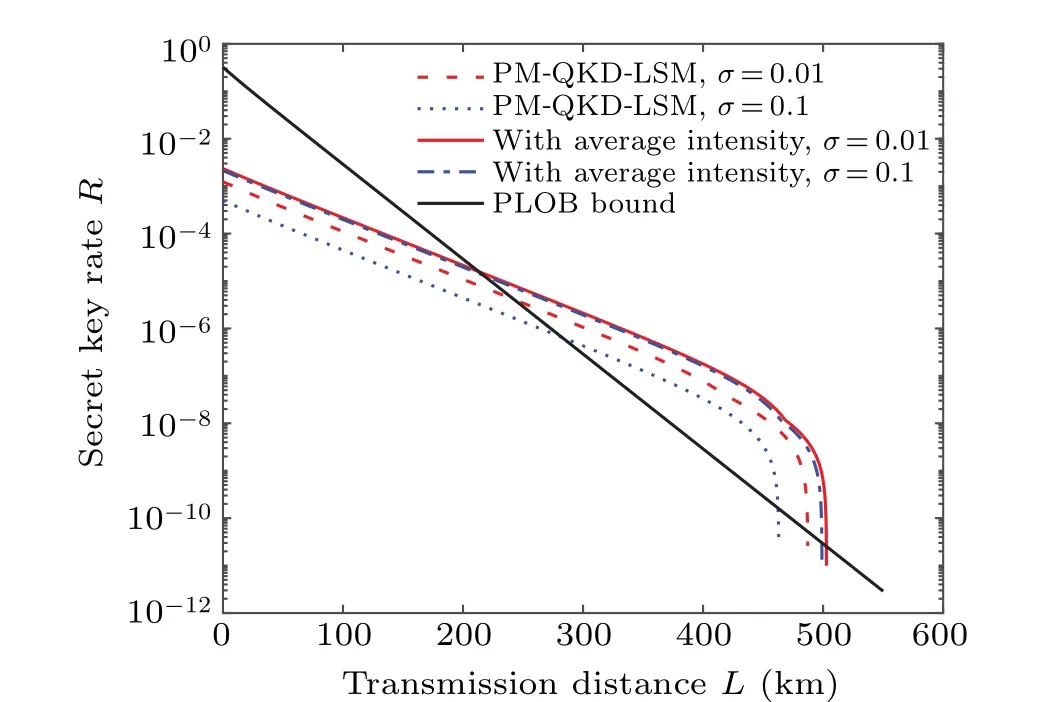
Fig. 4. The performance of the PM-QKD-LSM protocol and that of PM-QKD with average intensity method under different source fluctuation. For two different methods,a small fluctuation σ =1%(red curve)and a large fluctuation σ =10%(blue curve)are considered. The solid curves denote the PM-QKD-LSM protocol and dash-dotted curves denote the PM-QKD protocol with average intensity.

Fig. 5. The performance of the asymmetric PM-QKD-LSM protocol and the PM-QKD protocol without source fluctuate. The transmission distance is set to satisfy LB-LA =30 km, and the abscissa represents the total transmission distance(L=LB+LA).
We further consider the effect of the light source fluctuation on the asymmetric channel. The fluctuation coefficients are set up toσ=1%andσ=5%,respectively,and the other simulation parameters are the same as those in symmetric case.The results in Fig.6 indicate that the PM-QKD-LSM protocol has a better performance in the case of source fluctuation,even the source fluctuation is 10 times greater than that of asymmetry PM-QKD protocol.
In addition, we show the performance of the asymmetric PM-QKD-LSM protocol under different fluctuation coefficient versus the different Alice to Charlie transmission distance in Fig.7. The total transmission distance is set to 50 km,and the distance from Alice to Charlie is set from 5 km to 25 km. It can be seen from Fig. 7 that the performance of the asymmetric PM-QKD-LSM protocol with different source fluctuations are almost the same, which indicates the asymmetric PM-QKD-LSM protocol is also robust to the source fluctuation.that of PM-QKD protocol with source fluctuation. The symmetric and asymmetric PM-QKD-LSM protocol are robust to the source fluctuation. It is indicated that the PM-QKD-LSM protocol can still have a long transmission distance with the fluctuated source in practical QKD systems.
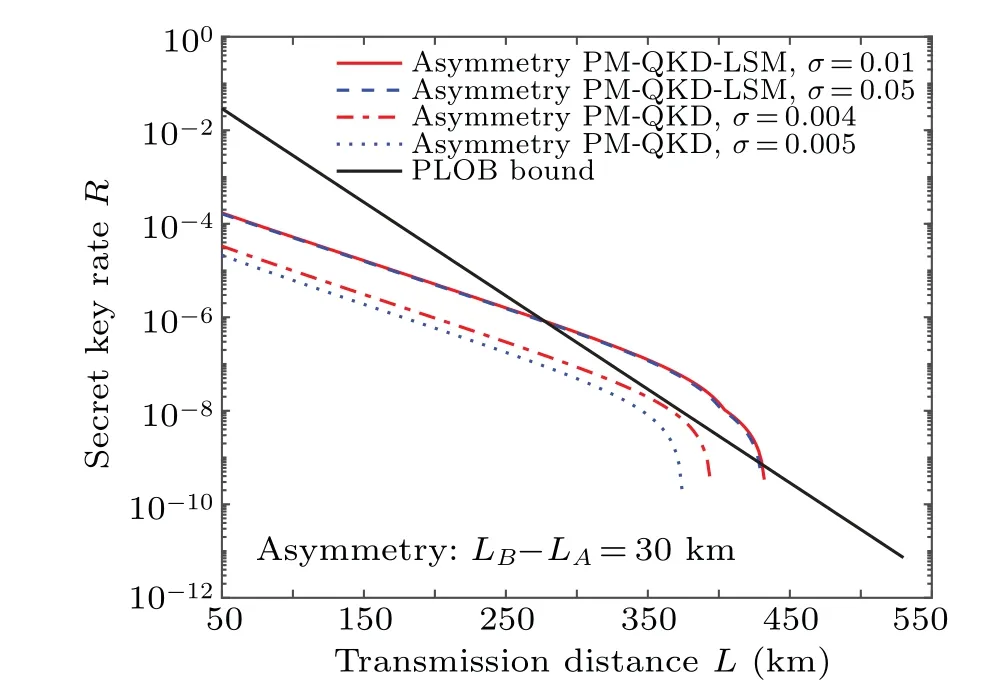
Fig.6. The performance of the asymmetric PM-QKD-LSM protocol for different Alice to Charlie transmission distance under source fluctuation. The transmission distance is set to satisfy LB-LA=30 km,and the abscissa represents the total transmission distance (L=LB+LA). The fluctuation coefficient σ =1% (solid curve) and σ =5% (dashed curve) in the asymmetric PM-QKD-LSM protocol are set, respectively. The fluctuation coefficient σ =0.4%(dash-dotted curve)and σ =0.5%(dotted curve)in the asymmetric PM-QKD protocol are studied,respectively.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 61871234 and 62001249) and Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University(Grant No.KF201909).

Fig.7. The performance of the asymmetric PM-QKD-LSM protocol under different fluctuation coefficient of light source. For the asymmetric channel, the fluctuation coefficient σ =0 (solid curve), a small fluctuation σ =1%(dashed curve)and a large fluctuation σ =5%(dash-dotted curve)are considered.
4. Conclusion
In this paper,we apply the LSM module to the PM-QKD protocol to solve the non-ideal source problem in practical QKD systems, where the LSM module is used to estimate the probabilities of zero photon,single photon and two photon precisely. We derive the more rigorous secret key rate under different source fluctuations.The results show that,whether in symmetric or asymmetric cases, the performance of the PMQKD-LSM protocol under UPC is almost the same as those of the PM-QKD protocol without source fluctuation. Moreover, PM-QKD-LSM protocol has a better performance than
- Chinese Physics B的其它文章
- Erratum to“Boundary layer flow and heat transfer of a Casson fluid past a symmetric porous wedge with surface heat flux”
- Erratum to“Accurate GW0 band gaps and their phonon-induced renormalization in solids”
- A novel method for identifying influential nodes in complex networks based on gravity model
- Voter model on adaptive networks
- A novel car-following model by sharing cooperative information transmission delayed effect under V2X environment and its additional energy consumption
- GeSn(0.524 eV)single-junction thermophotovoltaic cells based on the device transport model

