基于动态渗流阻力的产量劈分新方法

万茂雯，罗钰涵

（1.中国石化江苏油田分公司勘探开发研究院，江苏扬州 225009；2.中国石化江苏油田分公司开发管理部，江苏扬州 225009）

进入高含水期的层状油藏，层间矛盾日益突出，小层动用差异日益加大，动用较差层仍然具有一定的剩余油潜力。为进一步认识层间动用差异，评价剩余油在纵向上的分布潜力，有必要确立一套满足高含水期层状油藏的产量劈分方法，为开发后期实施精准挖潜提供依据。国内外学者在对开发后期油藏进行产量劈分时通常采用产液剖面法、流动系数法和动态劈分系数法［1-3］，其中产液剖面系数法能够反映实际生产动态，但往往由于动态测试资料不全，使得劈分精度低、可信度差；流动系数法假设所有有效厚度地层都有油量，此方法资料容易获取，劈分方法简单，但没有充分考虑储层的连通性、压差及物质与能量平衡，参数比较单一，通常无法满足实际需要；动态系数法对影响注水的动静态因素进行分析，但由于很多参数在实际应用中难以确定，因此计算难度大，不利于推广应用。

1 方法的提出

为满足开发后期多层油藏精细挖潜的要求，掌握各油井的分层动用状况，本文综合考虑地层渗透率、有效厚度等重要静态因素和动态渗流阻力参数的影响，建立多层并联活塞式渗流模型，根据计算得到的油水井间各小层的动态渗流阻力值劈分小层产量，并结合小层地质储量，明确各小层的剩余油潜力。

动态渗流阻力表征随饱和度变化的流体渗流能力，可根据达西定律［4］求得，两相流时，产液量计算公式为:

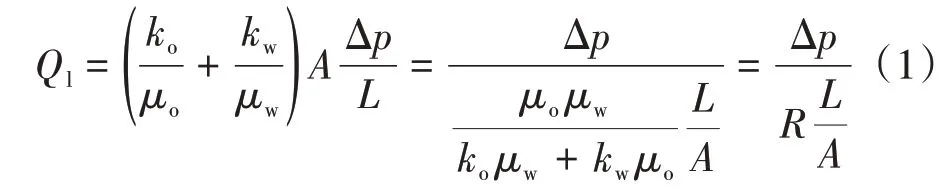
式中，Ql为产液量，m3；ko、kw为油、水相渗透率，µm2；μo、μw为油、水黏度，mPa·s；A为渗流面积，m2；Δp为渗流截面间的压差，MPa；L为渗流截面间的距离，m。

定义动态渗流阻力为:

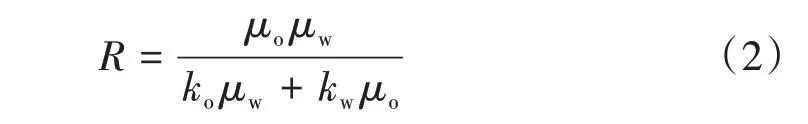
式中，R为动态渗流阻力，mPa·s/(µm2·m)。

由式（2）可以看出，动态渗流阻力与油水两相的相渗透率有关，而相渗透率是绝对渗透率和相对渗透率的乘积，其中绝对渗透率与静态地质条件相关，相对渗透率与油水两相饱和度相关。

2 模型建立与参数计算

2.1 模型建立

把多层油藏流体的流动看成是由多个单层一维线性流动的并联组合，各小层在井筒处耦合（见图1），以小层为单位，对模型参数进行求解。

图1 多层一维单向水驱油渗流模型示意

2.1.1 基本假设条件

①油藏在整个渗流过程中保持恒温；

②油藏中存在油水两相流体，并且符合达西定律；

③模型中考虑油、水两种组分；

④模型中流体的流动属于一维线性流动；

⑤油藏岩石具有微可压缩的性质，并且沿一维均质；

⑥油藏流体具有压缩性，模型中重力和毛管力忽略不计。

2.1.2 数学模型

基于以上假设，建立模型如下:

（1）运动方程:当流体线性渗流时，满足达西定律，渗流速度可以表示为:

考虑地层倾角，油水两相渗流速度的微分形式为:

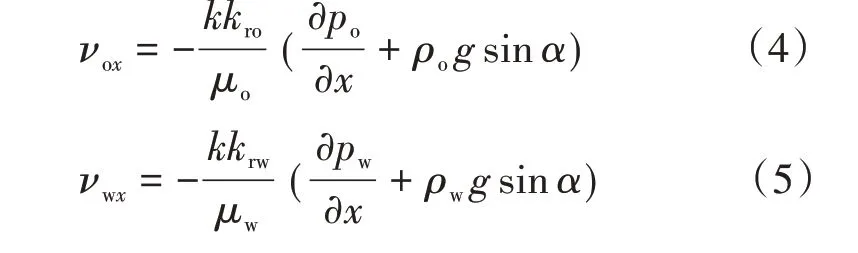
（2）连续性方程:流体渗流过程遵循质量守恒定律，又称连续性原理，即在渗流过程中任取一微小的单元体，该单元体内流体质量的变化等于同一时间间隔内液体的流入、流出质量之差，根据这一原理可得质量守恒方程，即连续性方程:

考虑油水两相，则连续性方程可以表示为:

式中，q为单位体积的质量流量，kg/(m3·s)；qo、qw为油、水在单位体积的质量流量，kg/(m3·s)；ϕ为孔隙度，小数；So、Sw为油、水饱和度，小数。

（3）辅助方程:

（4）初始条件:

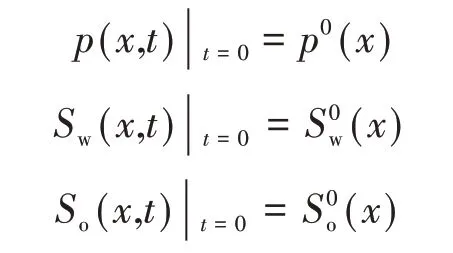
式中，p0(x)为油藏原始地层压力，MPa；(x)、(x)为油、水的初始饱和度值，小数。

2.2 关键参数计算

采用有限差分技术［5-6］，可以求解上述模型中油水井间任意位置的压力和饱和度变化值，从而求得相应的渗流阻力变化值，最终根据动态渗流阻力劈分小层产量。

2.2.1 压力计算

将油水两相的运动方程（4）、（5）分别代入各自的连续性方程（7）、（8）可得

其中

同理

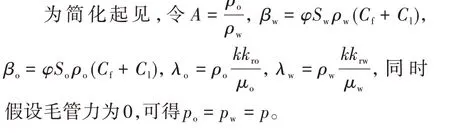
式中，Cf为岩石压缩系数，MPa-1；Cl为流体压缩系数，MPa-1；po、pw为油、水压力，MPa。

式（10）+式（11）×A，并进行差分处理，得到压力微分方程:

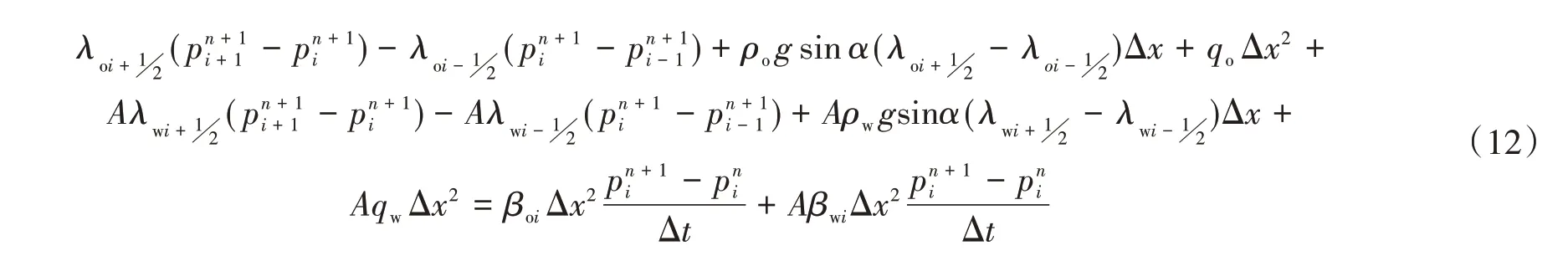
假设采用块中心均质网格，第1 个网格为注水井注水处，第n个网格为油井产出处，如图2所示。

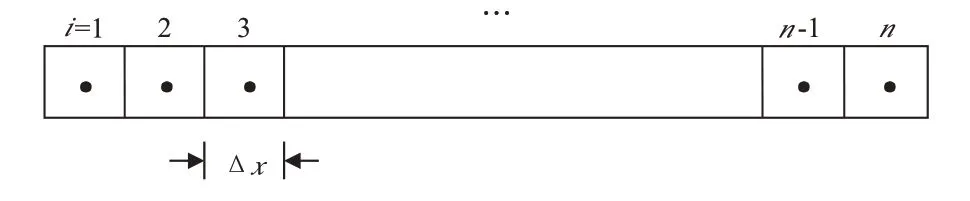
图2 一维水驱油块中心网格示意

分以下三种情况来讨论:

（1）对于处于中间位置的第2 至n-1 个网格，无注入水注入，也无液量采出，流体只在网格内部流动，故qw= 0，对式（12）采用上游权原则处理系数项λ，整理可得

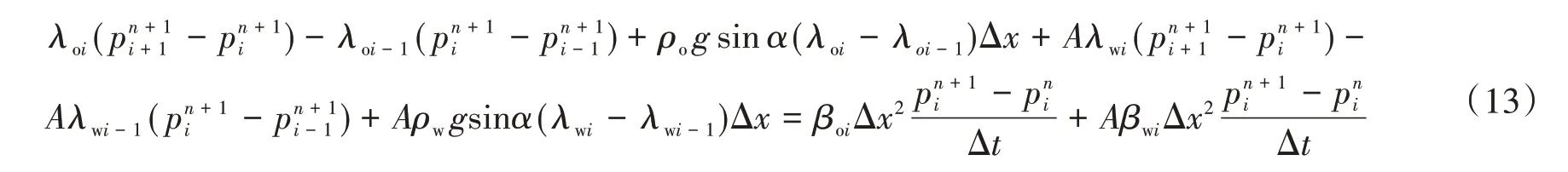
（2）对于水井所在的第1个网格，注水量为qw，p0=p1，整理可得

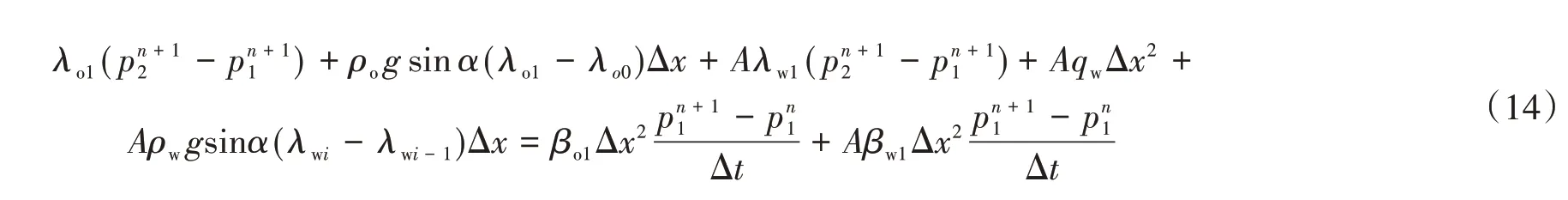
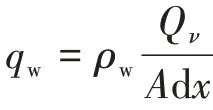
（3）对于油井所在的第n个网格，产液量为qv，pn=pn+1，整理式（8）可得

式中，qo为油的质量流量，即

联立式（13）、（14）、（15）得到三对角矩阵，求得油水井间任意位置的压力变化值，当i=n，此时的压力即油井处的压力pn。

2.2.2 饱和度计算

式（10）+式（11），进行差分处理，可以得到饱和度微分方程:

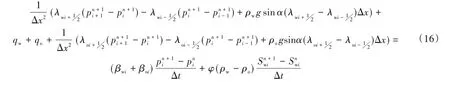
同理，分三种情况计算饱和度:

（1）对于第2 至n- 1 个网格，式（16）整理为:

（2）对于第1个网格，式（16）可以整理为:

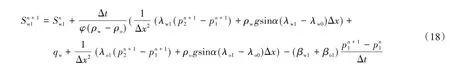
（3）对于第n个网格，式（16）可以整理为:

依次求解式（17）、（18）、（19）便可求得油水井间任意位置的饱和度变化值，当i=n，此时的饱和度即油井处的饱和度Sn。

2.2.3 动态渗流阻力计算

已知饱和度Sn，结合相渗曲线，得到该饱和度下油水两相的相对渗透率值kro、krw，代入式（2）可以得到油水井间任意位置的渗流阻力变化值，当i=n，即油井处的动态渗流阻力Rn。

2.2.4 小层产液量计算

将注采井间一共划分为n个网格，纵向上有m个小层，某一t时刻油井在第j层的压力和渗流阻力分别为pnj、Rnj，此时刻油井第j小层的产液量劈分系数为:

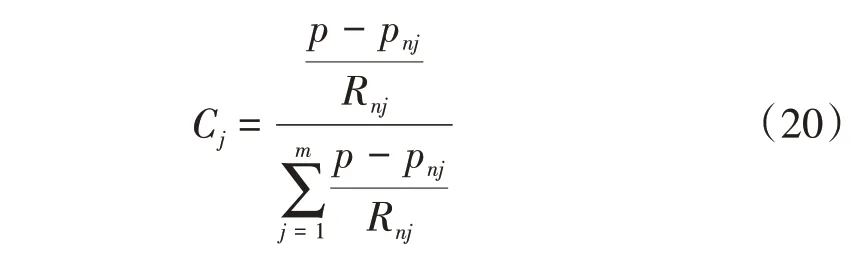
假设满足注采平衡，油井产液量Ql等于水井注水量Qi，用该时刻油井的产液量Ql乘以劈分系数，便可得到此刻油井的分层产液量Qlj:

2.2.5 小层产油量计算

根据t时刻油井处第j层的饱和度Snj，可以求得此刻油井处第j层的油水两相流度λonj、λwnj:

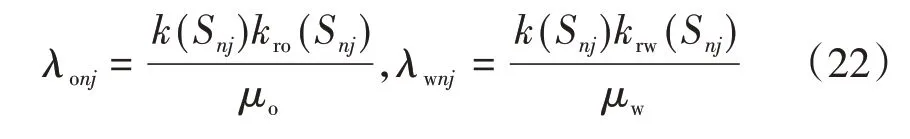
根据流度比劈分产油、产水量，得到t时刻油井的分层产油量Qoj:

Qoj对时间积分，便可求得油井在第j小层的累积产油量。

3 现场应用及验证

以YA 油田Y7断块为例，对20口油井进行产量劈分，解决了KH值劈分产量造成的储采矛盾。通过数值模拟对劈分结果进行验证，两种方法劈分结果符合率达80%以上（见表1），可满足现场需要。

表1 Y7断块戴一段二亚段（E2d12）砂体不同产量劈分方法结果对比

4 结论

（1）在有代表性相渗曲线的基础上，基于动态渗流阻力的产量劈分方法充分考虑了注采井间小层渗透率、有效厚度和油水饱和度的变化，符合地层非均质性强的特点，通过编制运算处理程序，可快速实现产量劈分，适合在现场推广应用。

（2）通过数值模拟对劈分结果进行验证，两者符合率高达80%，解决了传统KH值劈分产量导致部分小层产生储采矛盾，可以较准确地评价纵向潜力，为水驱开发油藏后期精细挖潜提供依据。