基于改进格子玻尔兹曼方法的砰击涌浪模拟
黄达 冯翔健















摘要 针对船舶与落石入水砰击涌浪灾害问题,采用浸入式边界-格子玻尔兹曼方法对二维楔形块入水涌浪问题进行了研究。从格子玻尔兹曼方法、基于流体体积法(VOF)的自由液面模型以及浸入式边界法的原理出发,阐述了其可以用来模拟有自由液面的流固耦合问题的理论基础,并优化了界面格子处浸入式边界力的求解方法。采用此方法模拟了楔形块体入水抨击实验,通过对模拟的块体速度与位置和实验结果进行比较,两者吻合良好,论文此方法模拟有自由液面的流固耦合问题具有较好的可行性。
关 键 词 格子玻尔兹曼方法;浸入式边界法;流体体积法;抨击问题;流固耦合
中图分类号 U661.1 文献标志码 A
Simulation of slamming surge based on lattice Boltzmann method
HUANG Da, FENG Xiangjian
Abstract The immersed boundary-lattice Boltzmann method is used to study the two-dimensional wedge block water entry. Based on the principle of the lattice Boltzmann method, the free surface model based on the volume of fluid method (VOF), and the immersed boundary method, we explain the theoretical basis that the combination of the three method can be used to simulate the fluid-structure interaction with a free surface. An improved method for calculating the immersed boundary force is presented. This method is used to simulate the slamming problem of the wedge block falling into the still water. The good agreements between the simulated results and the experimental results show that this method is feasible for the fluid-structure interaction with a free surface.
Key words lattice Boltzmann method; immersed boundary method; VOF; slamming problem; fluid-structure interaction
引言
準确地模拟有自由液面的流固耦合问题是计算流体力学中非常重要的问题之一,但是由于动网格的划分,这些方法往往会非常消耗计算资源[1],自He等[2-3]提出了格子玻尔兹曼方法(Lattice Boltzmann method,下文简称为LBM)以来,这种计算流体力学方法以其高效和无需划分网格的特性被广泛关注。近年来,格子玻尔兹曼方法作为一种基础计算流体力学方法,开始与其他方法进行耦合来拓展格子玻尔兹曼方法的应用领域;Feng与Michaelides[4-5]将浸入式边界法(IBM)与格子玻尔兹曼方法进行耦合来解决复杂边界的流固耦合问题,并验证了此方法的准确性,Chen等[6]采用IB-LBM来模拟包括非对称圆柱绕流在内的多种复杂几何流,但是传统的IB-LBM中流固耦合作用力处理复杂,会增大计算量,Suzuki和Inamuro[1,7]提出了一种通过迭代来计算流固耦合作用力的方法,简单且具有较高精度。而Körner等[8]将基于体积分数法(VOF)[9]的自由液面模型(FSM)与格子玻尔兹曼方法结合以描述自由液面的位置,并且用此方法模拟了气泡的演化,得到了很好的效果。但是,针对有自由液面的流固耦合问题目前的算法还尚有诸多缺陷,本文基于自由液面-格子玻尔兹曼方法并耦合浸入式边界法,提出了一种改良的边界力处理方法,并用此方法模拟了船舶海洋领域广泛存在的砰击涌浪问题,此过程是包括气、液、固三相的复杂流固耦合问题,在入水砰击瞬间会遭受巨大的抨击荷载。国内外学者对抨击涌浪问题进行了广泛的研究,邹丽等[10]对曲面楔形体入水抨击问题进行实验研究,表明在静水实验中外凸剖面模型产生的飞溅射流比反曲剖面模型更剧烈。陈小平等[11]研究了不同刚度的写形体入水抨击问题,探究了弹性效应对模型应变的作用。Yang等[12]基于浸入式边界法研究了楔形块入水问题,验证了浸入式边界法在解决入水问题的准确性。抨击涌浪的水体具有强非线性波,剧烈的波浪破碎等特点,可以用于验证此方法的准确性。
本文优化了界面格子处浸入式边界力的求解方法,并基于浸入式边界-格子波尔兹曼方法模拟了楔形块抨击涌浪问题,并通过与前人实验结果进行对比,验证网格收敛性,验证了此方法用于模拟带自由液面的流固耦合问题的可行性。
1 LBM、IBM、FSM的基本原理与方程
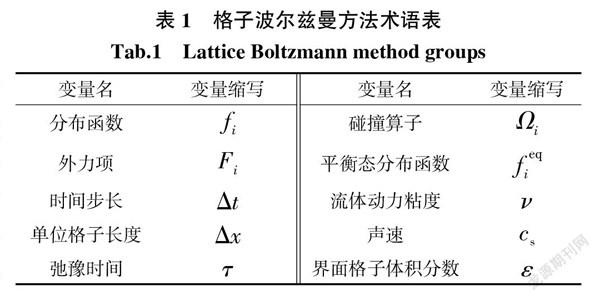
本部分主要对格子玻尔兹曼方法(LBM)、浸入式边界法(IBM)与自由液面模型(FSM)的基本原理进行介绍,着重介绍这3种方法耦合在一起以解决带自由液面问题的关键原因。为了方便讨论改良的浸入式边界-格子波尔兹曼方法,在下文中添加了术语表,术语表如表1所示。
1.1 格子波尔兹曼方法
对于流体的计算可以采用格子玻尔兹曼方法,LBM将流体按照笛卡尔坐标系划分为若干正方体网格,每个网格中存在由大量流体粒子组成的流体微团,而网格的划分也决定了模型的类别以及计算参数的差别,本文采用的是D2Q9模型,即二维模型且每个格子中的流体颗粒可以向着周围9个相邻格子运动,因此下文中均基于D2Q9模型对计算方法进行描述。
LBM基础变量为粒子的分布函数[fi(x,t)],代表在时间为[t]时,坐标[x]处,速度为[ci]的流体微团的密度大小,其中[ci]为在一个时间步长[Δt],流体颗粒向着相邻格子运动的距离,即[ci=(0,0),(0,±1),(±1,0),(±1,±1)]这9个向量。有外力作用的LBM的基本方程表述如下:
式中:[Fi]为外力项(本文中主要是重力),由Guo等[13]给出:
式中:[Ωi(x,t)]为碰撞算子,表示流体微团的碰撞。
也可以根据分布函数[fi(x,t)]的定义可以得到微观变量[fi(x,t)]、[ci]与宏观变量水的密度[ρ]、水的宏观速度[u]之间的换算关系:
因此,将上述方程总结起来便可得到有外力项的格子玻尔兹曼方法的碰撞与流动方程:
式中“*”上标代表碰撞之后流动之前的分布函数。
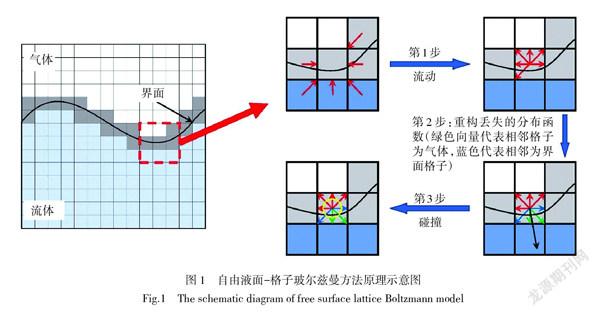
1.2 自由液面-格子波尔兹曼模型
自由液面模型(Free surface model, 下文简称FSM)与格子波尔兹曼方法的结合由Körner等[8]第1次提出,主要用于模拟计算流体力学问题中的自由液面,此方法中在这种方法中,LBM的介观格子被分为3类,完全是气体的气体格子,完全是液体的液体格子和包括气体和液体的界面格子,界面格子中定义了一个重要的变量——体积分数[ε=ε(x,t)],它代表了界面格子中流体占格子总体积的比值;气体格子和液体格子的相互转化只能通过界面格子来实现;由于气体格子内相应的平衡态分布函数在计算过程中被完全忽略,而为了满足界面格子的边界条件,在计算过程中需要重构缺失的分布函数,核心思想为:界面处,流体与气体的速度相等;气体所产生的力与流体产生的力相平衡。FS-LBM的基本原理与计算流程见图1。
重构步骤的基本原理是,我们知道气体的压强以及气体对流体的作用力,因此可以重构分布函数如下:
式中:[f*i]代表了碰撞后流动前的粒子分布函数,而下标中的[i]代表了[i]的反方向。[n]代表液面的法线方向指向流体内部,因此[n∙ci≥0]代表的就是那些缺失的粒子分布函数。气体密度与气压之间的关系可以用[ρG(t)=3pG(t)]来表示,而速度[v]代表的是界面格子处的流体宏观速度,即[v=v(x,t)]。
1.3 浸入式边界法
浸入式边界法(下文简称IBM)非常擅长处理复杂固体边界的流固耦合问题。此方法由最小作用量原理导出,包含两组变量:欧拉变量与拉格朗日变量,这2组变量由Dirac[δ]函数连接起来[14-15]。Paskin[14]第1次提出了IBM来解决心脏瓣膜附近的流动条件,通过在边界附近对流体施加适当的力,IBM可以将无滑移边界条件应用于笛卡尔网格中的任意形状边界,随后他[15]又详细阐述了用于计算机模拟IBM的数学结构,为IBM计算机数值模拟提供了思路。原理如下:此方法中固体边界节点采用拉格朗日坐标系,流体节点采用笛卡尔坐标系,其核心思想是:在进行固体与流体边界的处理时,通过Dirac[δ]函数将2个坐标系之间的分布节点力和插值速度联系起来:流固耦合作用力与位移通过光滑Dirac[δ]函数进行插值。Feng等[16]第1次将IBM与LBM结合,提出了直接力浸入式边界法(direct-forcing IBM)来解决流体与颗粒的耦合问题,由于整个流场都使用笛卡尔网格,涉及网格与坐标的转换,因此,这个方法能极大的提升计算效率,尤其是对于复杂动边界来说,这一优点尤为突出。图2a),b)展示了IBM的基本原理。在二维情况下,离散的浸入式边界法方程表达式为:
流体在欧拉坐标系统中被离散,坐标为[x],固体边界大约是拉格朗日坐标为[rj(t)]处的标记的总和,[u]与[F]是此格子处流体的宏观速度与受到的流固耦合力,[ub(rj)]为固体边界点的速度,[fj(t)]为拉格朗日节点上受到的流体给固体的力,[Δ(x-rj(t))]为Dirac[δ]函数。
2 多相流的浸入式边界-格子玻尔兹曼方法
2.1 单相流中浸入式边界力的求解
为了将IBM与LBM结合起来,首先需要解决的问题就是需要计算得到边界力:[F(x,t)]与[fj(t)],这一对作用与反作用力应当满足无滑移边界条件。这两个力有很多种计算方法,本文采用的是一种迭代求解浸入式边界力的方法:multi direct-forcing IB-LBM,这种计算方法比直接隐式求解[26]计算效率更高且操作起来更加简单。为了简单说明这种迭代求解方法,先以单相流为例,上标“[m]”代表迭代的次数,可以首先通过下式求得拉格朗日节点耦合力[fj]:
式中,[ub(rj)]是固体上坐标为[rj]的边界速度。之后将[f(m)j]通过1.3中的方法求得歐拉坐标系的流固耦合作用力[Fm(x)]之后,可以得到修正后的流体宏观速度:
随着迭代次数的增加,[u(m)(x)-u(m-1)(x)→0]。将之前迭代过程中得到的修正力[F(m)(x)]加起来就会得到总的流体受到的流固耦合力:
之后将得到的流固耦合作用力作为外力项参与流体计算,即可解决流固耦合问题。
2.2 多相流中浸入式边界力在界面格子与空气格子中的修正
对于多相流来说,与单相流不同之处在于除了液体格子,计算过程中还存在气体格子与界面格子,界面格子也同样有液体格子的性质,即界面格子同样有宏观速度[u(x)],因此这套流固耦合作用力计算方法在界面格子处同样适用,但是由于界面格子中流体的比例较少,因此应当乘以体积分数作为修正:
而对于气体格子,FSM中气体格子是没有给出宏观速度的,根据经验,气体对于固体边界的作用力一般是远小于液体的,若根据自由液面法中式(6)给出的补齐空气格子分布函数的方法,也只能补齐液面周围部分空气格子的分布函数,无法满足计算需要。
通过观察式(9)中浸入式边界法中流固耦合力的计算公式,拉格朗日节点耦合力的大小正比于拉格朗日节点和相邻的欧拉节点流体速度差,因此,若要使气体与固体间的作用力接近0,可以强制赋予拉格朗日节点相邻的空气格子一个与固体相同的速度,即:固体周围的气体格子的宏观速度为[u+ω×r],其中[u]是固体的平移速度,[ω]是滑块的旋转角速度,[r]是从固体形心到气体格子的矢量,具体原理可以参照图3a),b)。此速度计算公式代表了气体与固体之间的相对速度消除,根据拉格朗日节点耦合力的计算公式(9),流固耦合作用力为0。
3 多相流的浸入式边界-格子玻尔兹曼方法的模拟验证
为了验证多相流浸入式边界-格子玻尔兹曼方法(IB-FSLBM)的准确性,将于船舶抨击实验(自由落体楔形入水实验)所得的实验结果进行对比,Wang等[17]的实验结果将被采用,具体方法是采用与其实验设置相同的模拟情况,将入水过程中的流体液面、楔形滑块的速度与位置随时间的变化3个变量进行对比,观察得到的结果差别是否精确。
Wang等[17]的实验设置如图5所示,这是一个长3 m宽0.4 m高2 m的水箱,水箱中水面高度为1.2 m,一个自由下落的三角形棱柱自由下落到水面,此楔形棱柱的截面为等边三角形,高度为48 mm,长度为166 mm,宽度设置为396 mm,比水箱宽度小了4 mm,这是因为此实验是个二维实验,而滑块略小是为了避免其与水箱壁面的摩擦,其具体几何尺寸与质量已经标注在图4中。另外还有一些机械构造,保证楔形棱柱只有竖直方向平移这一个自由度。滑块底部的尖角与水面接触时的速度为[V0],而[V0]的改变是通过改变滑块的初始下落位置来决定的。在此实验中共设置了4种大小不同的[V0],选取其中2种情况进行模拟。本模拟计算域采用的格子数为1 200×800,时间步长为4×10-5 s。
在[V0=0.92m/s]的情况下,块体砰击导致涌浪,图5为实验过程中的照片与模拟流体速度场的对比图,其中左侧:红色实线为Wang等[17]采用边界元法(BEM)模拟得到的结果,黄色虚线为液面实际位置;右侧为使用IB-FSLBM模拟得到的速度场。在图5a)中,块体进入水中,两侧出现射流;图5b)中射流受到重力作用开始回落,图5c)、d)中流体开始向着中间空腔挤压,当时间t = 0.304 s时,空腔即将闭合。楔形块的下落速度[V]与下落位置[Y]见图6。块体速度先增加,后由于块体浮力与流固耦合作用力之和大于块体重力,块体速度开始降低,至最后阶段,空腔闭合回落的流体落在块体上块体速度出现波动。使用IB-FSLBM可以清晰的反映出块体速度先增加后减少的过程,块体在0.4 s内入水深度Y约0.44 m。
在[V0=2.5 m/s]的情况下,图7为实验过程中的照片与模拟流体速度场的对比图,与图5对比,可以清晰的发现,速度越大,射流也就越明显,而且在图7a)、b)中对比Wang等的数值模拟结果,可以发现IB-FSLBM对于射流形态的模拟更为精准,图8可以看出在较大的块体入水速度下,其速度基本呈现出单调递减的趋势,这与[V0=0.92 m/s]的情况完全不同,而块体在0.4 s内入水深度Y约0.55 m 。虽然较上一种[V0=0.92 m/s]的情况入水初速度增大了172%,但是相同时间内下落的速度却相差约25%。
通过进行对比,可以发现IB-FSLBM对于带自由液面的流固耦合问题具有可行性与良好的精度,满足模拟两相流自由液面流固耦合的要求。
为了探究本研究的网格收敛性,本文采用了4种不同的格子分辨率对上述2种情况进行验证,与实验相比,其相对误差如图9所示。总体上,随着网格分辨率的增加,相对误差逐渐减小,且通过比较单位长度的格子数为200与400的2种情况,网格分辨率基本已经收敛,而本文采用的单位长度的格子数为400,相对误差最大不超过4.01%,可以满足工程实际的需求。
4 结论
基于格子波尔兹曼方法、浸入式边界法及自由液面模型提出了可以解决有自由液面的流固耦合问题的IB-FSLBM,优化了空气与界面格子流固耦合力的计算方法,并用此方法模拟了砰击涌浪问题,得到如下结论。
1)通过固体的运动状态,将固体边界附近的空气格子赋予相同的速度,补全了空气格子处丢失的宏观速度,使空气格子与固体间无相互作用力;
2)由于界面格子处的流体并未充满格子,界面处流固耦合作用力应当小于同状态下的流体格子,因此在计算流固耦合作用力时应乘以体积分数作为修正;
3)使用此方法模拟了楔形块入水抨击实验,并将得到的结果和实验结果进行对比,具有较高的精确度,证明了此方法模拟自由液面的流固耦合问题具有可行性;
4)在砰击涌浪模拟中,在楔形块体初始入水速度为0.92 m/s时,块体入水受到的抨擊力较小,速度会出现先增加后减小的情况,而当楔形块体初始入水速度为2.5 m/s时,块体入水受到的抨击力较大,块体速度基本呈现出单调递减的趋势,入水速度越大,射流也就越明显。
参考文献:
[1] SUZUKI K,INAMURO T. A higher-order immersed boundary-lattice Boltzmann method using a smooth velocity field near boundaries[J]. Computers & Fluids,2013,76:105-115.
[2] HE X Y,LUO L S. Theory of the lattice Boltzmann method:from the Boltzmann equation to the lattice Boltzmann equation[J]. Physical Review E,1997,56(6):6811-6817.
[3] HE X Y,LUO L S. Lattice boltzmann model for the incompressible navier–stokes equation[J]. Journal of Statistical Physics,1997,88(3/4):927-944.
[4] FENG Z G,MICHAELIDES E E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems[J]. Journal of Computational Physics,2004,195(2):602-628.
[5] FENG Z G,MICHAELIDES E E. Proteus:a direct forcing method in the simulations of particulate flows[J]. Journal of Computational Physics,2005,202(1):20-51.
[6] CHEN D J,LIN K H,LIN C A. Immersed boundary method based lattice boltzmann method to simulate 2d and 3d complex geometry flows[J]. International Journal of Modern Physics C,2007,18(4):585-594.
[7] SUZUKI K,INAMURO T. Effect of internal mass in the simulation of a moving body by the immersed boundary method[J]. Computers & Fluids,2011,49(1):173-187.
[8] KÖRNER C,THIES M,HOFMANN T,et al. Lattice boltzmann model for free surface flow for modeling foaming[J]. Journal of Statistical Physics,2005,121(1/2):179-196.
[9] HIRT C W,NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics,1981,39(1):201-225.
[10] 鄒丽,李振浩,孙铁志,等. 楔形物体在静水与波浪中自由入水砰击试验研究[J]. 海洋工程,2019,37(1):1-11.
[11] 陈小平,李军伟,王辉,等. 大尺度楔形体板架钢模落体试验和仿真研究[J]. 船舶力学,2012,16(10):1152-1163.
[12] YANG L,YANG H,YAN S Q,et al. Numerical investigation of water-entry problems using IBM method[J]. International Journal of Offshore and Polar Engineering,2017,27(2):152-159.
[13] GUO Z L,ZHENG C G,SHI B C. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review E,Statistical,Nonlinear,and Soft Matter Physics,2002,65(4 Pt 2B):046308.
[14] PESKIN C. Flow patterns around heart valves:a digital computer method for solving the equations of motion[D]. Albert Einstein College of Medicine,Yeshiva University,1972:252-271.
[15] PESKIN C. The immersed boundary method[J]. Acta Numerica,2002,11:479-517.
[16] FENG Z G,MICHAELIDES E E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems[J]. Journal of Computational Physics,2004,195(2):602-628.
[17] WANG J B,LUGNI C,FALTINSEN O M. Experimental and numerical investigation of a freefall wedge vertically entering the water surface[J]. Applied Ocean Research,2015,51:181-203.
收稿日期:2021-03-29
基金项目:国家自然科学基金(41972297)
第一作者:黄达(1976—),教授,博士生导师,dahuang@hebut.edu.cn。

