基于分割嵌套三角剖分的重力场适配区选取算法

王 宇，肖 烜，刘绩宁，邓志红，王 博

（北京理工大学，北京 100089）

2021年3月发布的《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》中提出，要将深海探测作为科技前沿领域攻关，将精密重力测量研究设施作为国家重大科技基础设施。重力场是地球的固有物理场[1]，重力仪等测量仪器可以实时获得所在位置的重力异常信息，由于重力异常信息具有良好的时空位置特征，且不破坏水下航行器的隐蔽性，因此使用重力辅助惯性导航系统，能够安全、有效地提高惯性导航系统的导航定位精度。

适配区选取是水下重力辅助惯性导航系统的关键技术之一[2,3]。传统适配区选取算法主要有阈值法和单一特征值选取法等，主要对重力场统计特征参数进行比较分析[4]，而忽略了重力场的空间特点和几何特征，导致漏掉潜在的适配区域。

本文提出了一种基于分割嵌套三角剖分的重力场三维模型，首先利用墨卡托投影和重力异常空间校正，将传统重力场栅格信息变换为三维高程信息。再利用分割嵌套的思想，不断从重力场最小环形域中分割出最优三角形，从而形成重力场三角网络。对网络中每一个小三角形，选取了坡度、坡向、起伏度和粗糙度作为重力场局部几何特征，采用聚类算法，将重力场分为强适配区、弱适配区和非适配区，据此进行重力场适配区选取，使得适配区的选取更为有效。

1 重力场栅格信息预处理

1.1 经纬度数据投影变换

墨卡托变换可以使得投影坐标系更合适地描述不规则的重力场特征，对于重力场特征变化较为明显、起伏程度更大的区域可以表示得更加精确。将赤道作为标准纬线，本初子午线作为中央经线，赤道与本初子午线的交点作为坐标原点，取东向北向为正方向。根据等角条件，将地球表面的信息投影到一个平面上，地球表面的每一部分都对应相应平面上的微积线段，求得对应微积线段的关系式。然后先将地球近似视为一个标准的球体：在地球表面取一点A，假设A点在经纬度坐标系下的坐标为(λ,)φ，在墨卡托投影坐标系下对应的投影坐标为(x,y)，将赤道设置为基准纬线，用R表示地球半径。可得墨卡托投影方程式为：

最后推至更一般的表达式，将地球视为旋转中的椭球体，对应的(X,Y)=f(B,L)的墨卡托正解变换由式(2)表示：

式中，a为椭球体长半轴长度，取6378136.49 m，b为椭球体短半轴长度，取6356755.00 m，e为第一偏心率，取0.0818，e′为第二偏心率，取0.0821，N为卯酉圈曲率半径长度。

1.2 重力异常值z 因子转换

重力场数据在投影坐标系中的横、纵坐标单位为米，而重力异常的单位为毫伽（mGal），由于单位不同，因此将z因子作为重力异常值的转换因子，通过映射关系将重力异常值信息与高度信息之间建立联系，这样可以保证重力场三角剖分得到的三维曲面单位一致，都用长度单位米来表示。

根据重力异常空间校正的泰勒展开式，可以将空间校正看作将大地水准面上的正常重力值γ0()φ进行延拓至高度h上的正常重力值与原来高度的差异。将高程信息h作为地球半径R的增量，可得：

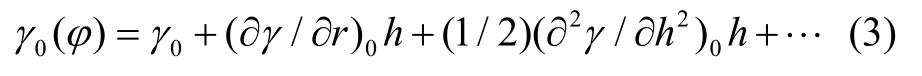
其中误差项即为高度校正值：(∂γ/∂r)0h+(1/2)(∂2γ/∂h2)0h+…。

若将地球看作扁率为f的椭球，可得与平静海平面处于一致状态的大地水准面上的一点正常重力值g0与该点高程为h处的正常重力异常值gh之间满足以下方程：

其中ge为地球赤道上的重力值；R为地球的平均半径；q为赤道上惯性离心力与引力之比；φ为地理纬度。

地球参数采用ge=9780300mGal，R=6371.2km，f=1/298.3，q=0.003467。得到空间校正公式近似为：

若进行进一步的简化，将地球看作半径为R的均质圆球，则距离地面高度h处的重力值为：

对应的大地水准面上点的引力为：

将式(6)(7)作差可得：

将地球半径和地球平均重力代入可得一阶近似公式：

由此可得，每1 m 的高程位移产生约0.3086 mGal的重力异常变化。由式(2)(10)可以将经纬度信息、重力异常值信息进行数据预处理，转化为以米为单位的坐标。如将图1的重力场传统栅格信息经过墨卡托投影变换后得到图2所示区域。

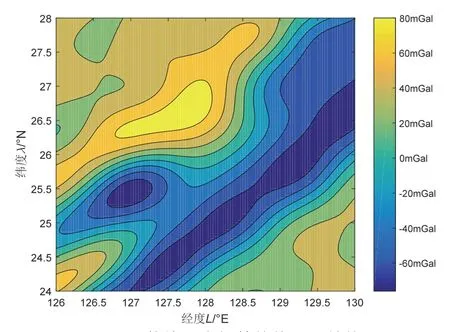
图1 传统重力场等值线平面结构Fig.1 Plane structure of isoline of traditional gravity field

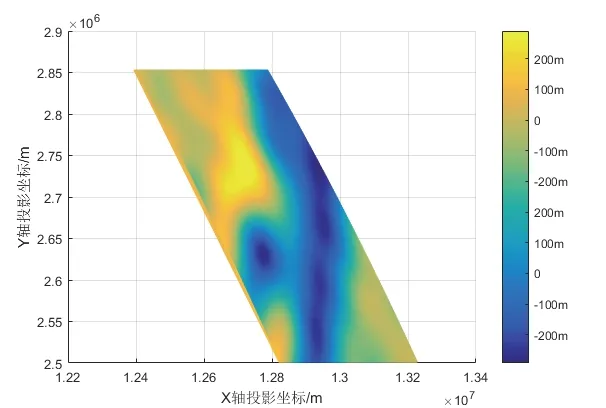
图2 墨卡托投影变换后的等值线图Fig.2 Contour map after Mercator transformation

2 基于分割嵌套三角剖分的重力场三角网络构建

重力场三角网是根据已知的传统重力场重力异常栅格点及其中蕴含的位置等信息，通过三角剖分等处理方式，将这些点按照一定规则、一定顺序串联起来，构成由互不相交、互不重叠的三角形形成的三角网络[6]。这种三角网络对于处理复杂重力曲面信息，分析其中的拓扑结构具有重要作用，因此可以用构建重力场的三角网络来对重力场几何拓扑特点进行分析和提取[7]。

在构建重力场三角网络时，需要利用三角剖分算法。常用的三角剖分算法例如Delaunay 三角剖分[8,9]，这种算法更侧重于对三维立体结构进行剖分，更适用于对某个场立体特征的分析。而本文提出的基于分割嵌套环形域三角剖分算法能够较为准确地对重力场表面的信息进行描述，可以将重力场背景图中提供的重力场点集的几何特征表现出来，且算法的可行性较高，复杂度较小，还可以解决许多较常见三角剖分算法无法解决的最小权三角剖分的实现问题，所以在构造重力场三角网络时采用这种基于分割嵌套的三角剖分算法。

将重力场背景图中提供的重力场点集经坐标变换投影到经度-纬度坐标平面上，由此得到一组平面重力场点集，再将平面重力场点集中全部点组成一个凸壳，通过不断筛选凸壳中的顶点，找到位于最内层的嵌套凸壳，从此开始可以分为三种情况：最内层凸壳不包含、包含1 个，或者包含2 个平面重力场点集中的点。包含3 个或3 个以上平面重力场点集中的点的情况是不可能发生的，因为如果平面重力场点集中有3 个点都位于筛选得到的最内层凸壳中，则该凸壳中还可以继续划分出一个位于其内侧的凸壳，也就意味着它不能作为嵌套区域中最内层的凸壳。

接下来对三种情况分别处理。若最内层凸壳中不包含平面重力场点集中的点，则求出该凸壳的直径，从中取点作为判断时的顶点，判断凸壳中点的共线情况，将不共线的点与其他点连成线段，比较所得线段之间的长度，删去长度较长的线段，保留长度较短的线段，对每个不共线的点都进行这样的步骤，直到将整个凸壳完全分割成三角形。若最内层凸壳中包含1个平面重力场点集中的点，则将该点分别与凸壳的各顶点相连接，将这些连成的线段按照本身的长度由大到小的顺序排序，得到对应的凸壳顶点的序列，再将这些凸壳顶点按顺序作为判断时的顶点，判断凸壳内部的共线情况，将不共线的点与其他点连成线段，通过比较线段长度的大小关系，对线段进行添加和删除，直到将整个凸壳完全划分为三角形。若最内层凸壳中包含平面重力场点集中的2 个点，则将这2 个点连接成一条线段，取凸壳中位于该线段右侧的点，将该点分别与最内层凸壳包含的平面重力场中的2 个点相连接，这样就形成了一个完整的凸壳，在新得到的凸壳中判断点与线的位置关系，再通过线段长度的比较进行筛选，将该凸壳进行划分，直至使之成为全部由三角形构成的凸壳。

在对平面重力场点集中最内层嵌套凸壳处理后，再对中间的环形区域进行划分，可以取出一条固定边，分别选出环形区域中位于固定边同一侧的点链，将固定边的两个端点分别与该点链相连接，由此形成一个新的凸壳，再用与处理最内层相同的方法对其进行划分，即可得到完整的三角剖分结果。分割嵌套环形域的三角剖分算法流程图如图3所示。

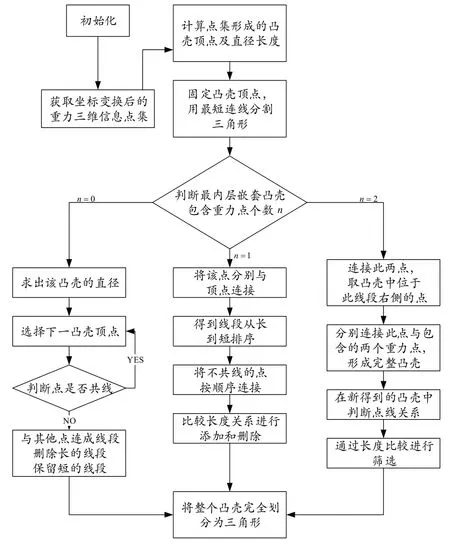
图3 分割嵌套环形域的三角剖分算法流程图Fig.3 Flow chart of triangulation algorithm for segmenting nested ring domain

3 重力场三角网络几何特征选取

从经过三角剖分后的重力场三角网络中，可以提取重力场几何空间特征参数来对重力场特征，尤其是局部特征进行分析，进而更加合理、更加精确地描述重力场三维表面特性。本文提取的重力场几何空间特征包括：坡度、坡向、起伏度和粗糙度[10]。其中，坡度和坡向能够表现重力场局部三角形法向量在俯仰角及旋转角上的变化。起伏度和粗糙度能够表征重力场局部曲面变化特征及起伏程度。

3.1 坡 度

坡度为重力场三角面的法线矢量与z轴矢量的夹角，可以表示重力场曲面局部的最陡坡倾斜程度，是每个三角面中的最大重力异常变化率。坡度值的范围为0°～90°。坡度值越小，重力场曲面变化越平缓，坡度值越大，重力场曲面变化越陡峭。坡度slope的表达式如下：

3.2 坡 向

坡向为重力场三角面的法线矢量在水平面的投

影矢量与正北方向矢量的夹角，可以表示曲面的水平方向，是坡度所面对的方向。坡向按照顺时针方向进行测量，坡向角度范围介于0°（正北）到360°（仍是正北）之间，即完整的圆。坡向可以用于识别重力场曲面某一位置处的最陡下坡方向。坡向aspect的单位为°，表达式如下：

其中，nx表示标准法线矢量在x轴的分量，ny表示标准法线矢量在y轴的分量。

3.3 起伏度

起伏度是指重力场三角面内最大的重力异常值zmax与最小重力异常值zmin之差，是描述重力场特征的一个宏观性指标，起伏度反映的是区域内重力场起伏变化的特征，起伏度越大，则说明重力场特征变化越丰富。起伏度relief的单位为mGal，表达式如下：

3.4 粗糙度

粗糙度是重力场空间三角面积S与其在水平面上的投影面的面积S' 之比，它是描述重力场曲面的侵蚀程度的重要指标，粗糙度越大，则说明重力场空间表面越曲折，特征变化越丰富。粗糙度rough表达式如下：

4 基于k-means 的适配区聚类分析

为了利用重力场三角网络的几何特征，需要对其进行数据挖掘。k-means方法是一种经典的迭代求解聚类分析算法，被广泛应用在机器学习、图形分析领域。本文利用k-means方法对4 个重力场几何特征值进行聚类分析，从而将重力场按照适配性划分为3 种区域：强适配区、弱适配区和非适配区。

从重力场三角网络中随机选取3 个三角面的4 个标准化处理后的几何特征值作为初始聚类中心，计算其余三角面的标准化几何特征值到这些聚类中心的相似性度量。本文采用的欧氏距离度量如下：

其中，i,j为重力场三角网络中局部三角形编号，xij为重力场三角面的标准化几何特征值。

根据相似性度量的计算结果，将不同的重力场三角形分配给相似度最高的聚类中心，更新聚类中心并重新分配几何特征值，在聚类过程中使用的聚类准则函数为：

其中，mij为聚类中心特征向量，E为均方差之和。重复迭代更新聚类中心和特征向量分配环节，当E的值不变时，代表算法收敛，最终将重力场按照适配性划分为3 种适配区域。

图4 基于三角剖分的适配区选取流程图Fig.4 Flow chart of area selection based on triangulation

5 仿真实验结果及分析

选取北纬24°～28°，东经126°～130°范围的重力场背景图进行实验，分辨率为1′×1 ′，经改进克里金算法将其插值为0.5′×0.5′，其中重力异常值最大为91.09 mGal，最小为-75.97 mGal。在仿真中，x轴、y轴坐标为墨卡托投影变换后的经度、纬度坐标，z轴为经过重力异常空间校正变换后的重力异常值。采用本文提出的基于分割嵌套三角剖分算法，将传统的重力场等值线平面格网结构，变换为重力场立体三角网结构，如图5所示。形成由115198 个小三角形组成的连续三角面，来描述重力场的几何拓扑特征。

图5 嵌套分割三角剖分后的局部重力场立体三角网结构Fig.5 Three dimensional triangulation structure of local gravity field after nested segmentation triangulation

在经过三角剖分后的重力场三角网中，选择每一个局部三角形的坡度、坡向、起伏度和粗糙度作为重力场几何空间特征参数。4 个特征参数在仿真区域内的空间分布如图6所示。

图6 重力场坡度、坡向、起伏度和粗糙度空间分布图Fig.6 Spatial distribution of gradient,aspect,fluctuation and roughness of gravity field

经过对坡度、坡向、起伏度和粗糙度的k-means聚类后，得到的该区域内重力场适配性如图7所示，其中深蓝色区域代表强适配区，黄色区域代表弱适配区，绿色区域代表非适配区。同时采用传统的阈值法多指标融合方法，选取重力场标准差和经纬度方向相关系数作为重力特征参数[14]，并通过经验确定阈值k=10，应用阈值法得到最终选取标准，并在同一片区域内进行适配区选取，得到的结果如图8所示。

图7 3 种重力场适配区空间分布图Fig.7 Distribution map of three gravity adaptation areas

图8 传统阈值法适配区选取结果Fig.8 Selection results of adaptation region of traditional threshold method

结合图7-8 可以看出，同一片重力场内，传统方法与本文所提方法在适配区的选择上有较大不同，主要体现在图8的三片区域内。传统阈值法将区域1 和区域2 划分为非适配区，区域3 作为适配区，而本文所提出的适配区选取方法，将区域1 作为强适配区，区域2 作为弱适配区，而区域3 作为非适配区。传统阈值法过于强调参数阈值的作用，而缺少多指标融合的手段，忽略了重力场的空间特点和几何特征，导致漏掉潜在的适配区域。

本文算法选出来的强适配区（如区域1），重力场的坡度较大，坡向变化明显，同时起伏度和粗糙度较大，表明该区域内，重力场的几何空间特征明显，重力异常信息丰富，适合进行重力匹配定位。根据仿真结果，选择图7中红圈内区域（即图8中的区域1）作为适配区，规划水下航行器的仿真轨迹。设航行器在水下进行匀速直线运动，航行速度为20 节（约10.289 m/s），航向为西北方向，设定航行时间为150 min。陀螺常值偏移为0.01°/h，陀螺随机误差为0.001°/h，加速度计零偏为100 μg，随机误差为50 μg。

如图9所示，黑色的曲线是水下航行器的真实轨迹，蓝色的曲线是惯性导航系统输出轨迹，可以看出经过一段时间的航行后，INS 输出轨迹逐渐发散，偏离真实轨迹。而红色的曲线代表基于ICCP 算法的重力匹配航迹，与真实轨迹几乎重合，匹配定位平均位置误差与重力场背景图网格分辨率相当。表1为重力匹配定位解算结果。仿真结果表明，本文所提算法能够选择被传统适配区选取算法漏掉的强适配区，在此适配区内，重力匹配定位效果好，精度高。

图9 强适配区内重力匹配定位航迹图Fig.9 Gravity matching positioning track map in strong adaptation area

表1 强适配区内重力匹配定位误差Tab.1 Gravity matching positioning error in strong adaptation area

6 结 论

本文针对传统重力场适配区选取算法缺乏对重力场三维信息、局部信息充分利用的问题，提出一种基于分割嵌套三角剖分的重力场适配区选取算法。首先利用墨卡托投影和重力异常空间校正，将传统重力场栅格信息变换为三维高程信息。再利用分割嵌套的思想，不断从重力场最小环形域中分割出最优三角形，从而形成重力场三角网络。对网络中每一个小三角形，本文选取了坡度、坡向、起伏度和粗糙度作为重力场局部几何特征，采用k-means聚类算法，将重力场分为强适配区、弱适配区和非适配区。在强适配区内，重力场的坡度较大，坡向变化明显，同时起伏度和粗糙度较大。仿真实验结果表明，基于分割嵌套三角剖分的重力场适配区选取算法弥补了传统方法描述重力场特征时单一、片面的缺陷，能够挖掘出重力场更多的局部信息减少了人工干预和人工经验判断，更加全面客观地划分适配区。未来可以继续针对三角剖分后的重力场进行几何特征挖掘，同时将轨迹信息也进行相似处理，利用重力场三角形和轨迹三角形进行基于计算几何的匹配算法研究。