高速列车齿轮偏心下的轮轨作用动态特性

宋德刚， 李智国， 王志伟

（1.中车青岛四方机车车辆股份有限公司，山东 青岛 266111；2.西南交通大学 机械工程学院，成都 610031）

0 引言

我国高速列车服役里程的不断增加及复杂线路的陆续开通，严重挑战列车运营安全。齿轮传动系统是高速列车核心部件，其功能是将来自牵引电动机的转矩传递至轮轨界面，从而驱动车辆前进。传动系统的动力学行为、结构的优劣将直接影响高速列车的服役性能[1]。当传动系统出现故障或者严重失效时，将威胁行车安全，甚至导致高速列车脱轨[2]。因此，研究齿轮传动影响下的轮轨动态作用，掌握齿轮失效状态下的轮轨动态特性，对保障列车安全运行具有重要的理论价值及工程意义。

高速列车齿轮传动系统采用单级传动方式，服役过程中齿轮传动系统承受着内部啮合带来的振动，同时也承受着来自轮轨和牵引电动机的激励。齿轮传动的动态行为反过来也会影响轮轨作用。目前大量研究往往集中于外部激励对传动系统的影响，主要包括牵引力矩、车轮扁疤、车轮多边形等因素下传动系统的振动行为[3-4]。结果表明，牵引力矩波动、车轮扁疤、车轮多边形和轨道不平顺激励均会明显影响传动系统动态行为，甚至导致齿轮箱箱体裂纹。此外，传动系统的啮合特性也会影响车辆系统的耦合振动，例如引起轴箱轴承和轮对的高频振动[5-6]。然而，目前很少有关于齿轮传动作用对轮轨特性影响的研究，对于高速列车驱动过程中轮轨动态行为的认识不够充分，有待进一步研究。

围绕齿轮传动系统作用下的轮轨动态特性问题，本文基于车辆系统动力学、齿轮传动系统动力学和轮轨关系，建立了考虑车辆耦合振动的齿轮传动系统动力学分析模型。为了有效揭示车辆系统在牵引力矩作用下的轮轨动态行为，该模型详细考虑了齿轮传动非线性特性、减振器非线性阻尼特性、轮轨非线性几何关系及接触关系等非线性因素。基于建立的动力学模型，本文系统地研究了不同偏心量和不同速度下高速列车轮轨动态行为，可为高速列车的安全运营提供有效的理论支撑。

1 考虑传动系统的高速列车车辆动力学模型

1.1 齿轮偏心动力学模型

我国高速列车传动系统采用单级齿轮传动方式驱动车辆前进。某型高速列车的齿轮箱分别通过“C”型托架和轴承安装于构架和车轴。为了分析齿轮偏心对轮轨特性的影响，本文忽略传动系统结构的柔性变形，建立某型高速列车单级传动的齿轮偏心动力学模型，如图1所示。

图1 齿轮传动系统动力学模型

基于传动系统结构特性和工作原理，其动态啮合力在轴向上的分力为式中：Yp、Zp分别为小齿轮轴向、垂向位移；Mp为小齿轮质量；Ipx、Ipy分别为小齿轮绕X、Z轴的转动惯量；Kmp、Cmp分别为柔性联轴节的扭转刚度、阻尼；Fpgy为作用于小齿轮横向力；FpgzL、FpgzR分别为作用于小齿轮左、右两端的垂向力。FpgzL、FpgzR可由下式获得：

1.2 整车动力学模型

基于国内某型高速列车结构参数，通过SIMPACK平台建立了高速列车三维整车动力学模型，如图2所示。

如图2所示，模型主要包括车体、构架、牵引电动机、齿轮传动系统、轮对和轴箱等关键部件。模型中，各个部件之间通过铰接或者三维弹簧-阻尼单元连接。悬挂系统的非线性特性，比如减震器和横向止挡的非线性特性，通过相关函数进行模拟。与传统车辆系统动力学模型相比，该模型考虑了齿轮传动系统与车辆系统动态耦合关系，能够模拟齿轮偏心与车辆动力学响应耦合关系。

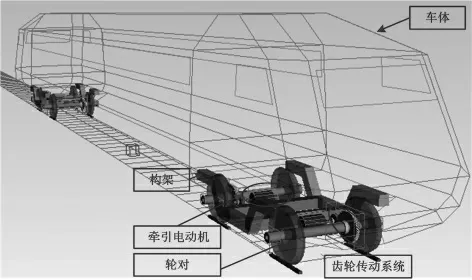
图2 考虑齿轮传动系统的车辆动力学模型

在本文建立的车辆动力学模型中，将车体、构架、牵引电动机和轮对均视为刚体，考虑了6个方向的自由度。关于齿轮传动系统，由于安装方式及模型简化等原因，本文仅考虑了部分自由度。最终，高速列车车辆动力学模型共包括114个自由度，如表1所示。

表1 车辆相关部件自由度

1.3 轮轨关系

轮轨关系是车辆和轨道系统的纽带，轮轨界面激励向上作用于车辆系统，向下作用于轨道系统。本文通过迹线法求解车轮和轨道接触点位置[8]，然后获得第i轮对在t时刻左、右轮的相对位移：

式中，Zwi是第i个轮对质心的垂向位移。根据轮对位移及几何关系，可以得到左、右两侧轮轨法向压缩量：

式中，G和Z（t）分别为轮轨接触常数和轮轨弹性压缩量。采用文献[9]中计算方法实现轮轨蠕滑力计算。

2 验证及结果分析

与经典车辆动力学模型相比，该模型能够模拟和揭示不同偏心量对轮轨动态行为的影响。本节首先通过线路试验验证模型的准确性，然后基于建立的耦合动力学模型分析齿轮偏心对轮轨作用的影响。

2.1 试验验证

在高速列车线路试验中，通过加速度传感器测试构架和轴箱垂向振动加速度。测点位置如图3所示，采样频率为1000 Hz。车速为300 km/h的构架和轴箱垂向振动加速度如图4所示。为了进行对比分析，图中也列出了模型计算结果。可以发现，实测的构架和轴箱最大垂向振动加速度分别为1.1g和8.7g，仿真分析所得的构架和轴箱垂向最大振动加速度幅值分别为0.9g和7.6g，二者的误差分别为18.1%和12.6%。试验和仿真所得的构架振动加速度有效值分别为0.32g和0.30g，误差为6.3%；试验和仿真所得的轴箱振动加速度有效值分别为4.6g和4.2g，误差为8.7%。上述结果表明仿真和测试结果存在一定误差，这是由于建模过程中模型的简化、忽略了部分摩擦因素及难以准确获取服役过程中轮轨状态所致。总体来说，仿真与试验测试的轴箱及构架振动加速度结果大体一致，模型的有效性得到验证。

图3 线路试验振动加速度测点

图4 加速度时间历程曲线

2.2 齿轮偏心对轮轨动态特性影响分析

基于建立的动力学模型，分析齿轮偏心对轮轨动态特性影响。仿真速度设置为300 km/h，车轮偏心量为3 mm，仿真过程中考虑轨道几何随机不平顺激励，轮轨力结果如图5所示。可以发现，当齿轮出现偏心时，轮轨动态作用会明显加强：轮轨纵向力最大值从11.4 kN增加至32.2 kN，增加了182.5%；轮轨横向力最大值从6.9 kN增加至16.4 kN，增加了137.7%；轮轨垂向力最大值从89.3 kN增加至130.6 kN，增加了46.1%。具体结果如表2所示。轮轨纵向力时间历程曲线经快速傅里叶变换获得的频谱结果，由于轮轨横向力和垂向力频谱类似于纵向力结果，这里不再重复给出。可以发现，当齿轮出现偏心时，轮轨力出现了70 Hz的主频及其倍频，纵向轮轨力的波动主要由齿轮偏心决定。

表2 轮轨力最大值结果对比

图5 齿轮偏心对轮轨力影响的仿真结果

为了考察不同速度等级、不同齿轮偏心程度对轮轨力的影响，以50 km/h为间隔，计算了速度等级100 ～300 km/h 区间，偏心量分别为1、2、3 mm 时 的 轮轨力最大值，结果如图7所示。可以看出，当齿轮偏心量小于2 mm时，轮轨力受到的影响可以忽略；当齿轮偏心量大于2 mm时，轮轨力明显受到齿轮偏心的影响。当驱动力矩和偏心量一定时，车辆运行速度越高，齿轮偏心对轮轨动态作用影响越明显。

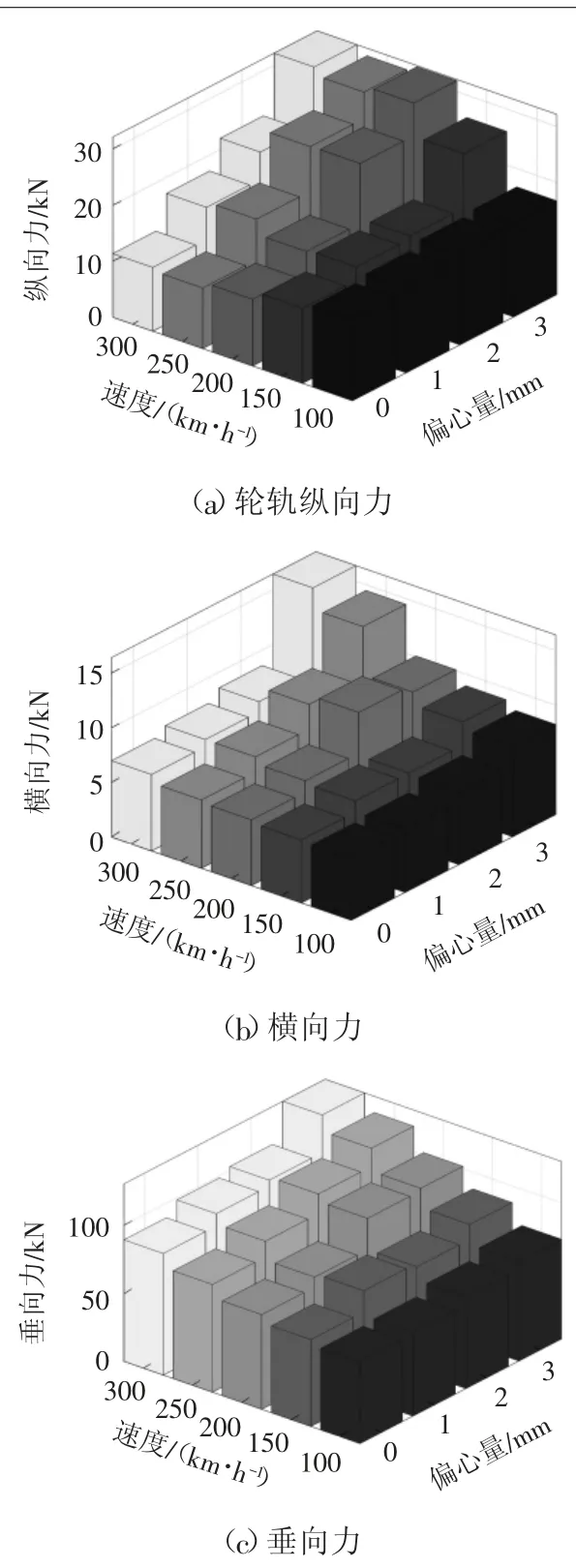
图7 轮轨力最大值统计

当齿轮出现偏心时，齿轮啮合出现周期性激励。由于传动系统大齿轮直接安装于轮轴，啮合力从啮合位置直接传递至轮轴，导致车轮呈现周期性的扭转振动。车轮扭转振动直接影响轮轨界面，导致轮轨纵向力、横向力和垂向力产生周期性波动。因此，当齿轮出现偏心时，轮轨界面会不可避免地受到不同程度的影响，特别是高速情况，这样的影响不可忽略。

图6 轮轨纵向蠕滑力频谱图

3 结论

本文建立了考虑齿轮偏心的高速列车车辆动力学模型，模型详细考虑了高速列车结构和几何非线性因素，包括轮轨非线性、齿轮传动系统非线性、悬挂系统非线性特性。相比于传统车辆系统动力学研究，该模型能够揭示传动系统与轮轨系统的动态耦合作用，并通过了试验验证。

计算结果表明，齿轮传动系统与轮轨系统存在明显的耦合现象。当齿轮出现偏心时，传动系统的扭转振动会直接导致轮轨扭转振动加剧，然后进一步导致轮轨作用加强。与没有出现偏心时相比，轮轨纵/横/垂向力最大值从11.4 kN/6.9 kN/89.3 kN增加至32.2 kN/16.4 kN/130.6 kN。因此，在分析轮轨作用时，特别是在高速运行条件下，不应忽略齿轮传动系统的影响。