基于DEFORM-3D有限元模拟的高速铣削刀具偏心跳动分离与辨识研究

殷红梅，赵连星，汪木兰

（1.江苏电子信息职业学院 数字装备学院，江苏 淮安 223003；2.南京工程学院 江苏省先进数控技术重点实验室，南京 211167）

0 引言

随着信息技术的飞速发展，利用三维有限元模拟高速铣削物理状态被验证为一种高效的铣削应力分析途径，被越来越多地运用在复杂工况下铣削力建模与预测、残余铣削力分析及工件终端切削成形等金属切削领域研究中。广西大学黎宇嘉等[1]利用Ti6Al4V铣削过程,采用有限元仿真软件Deform-3D获取铣削参数，分析获取粗糙度与能耗数据，继而用改进的高斯过程回归优化重构粗糙度与能耗模型，并最终通过物理试验证明该方法在精度与动态响应上更具优势。同课题组黄兵[2]则利用DEFORM-3D构建了涂层TiAlN硬质合金刀具铣削钛合金过程的有限元模型，进而构建了高斯过程回归-多目标粒子群算法的优化模型。重庆大学白云龙[3]利用有限元分析研究基于旋风铣削的切屑时变特性，针对旋风铣削切屑宏观与微观形态及其特性展开了试验研究。刀具偏心跳动是高速铣削时不可忽视的重要参数，直接影响着工件表面质量与刀具寿命。近年来，刀具偏心跳动的宏观特性与微观算式被国内外学者多次研究。本文利用DEFORM-3D有限元软件对高速铣削中三维斜角切削进行有限元模拟，以硬质合金平头立铣刀加工AL6061-T6为试验对象，建立瞬时铣削力与瞬时铣削厚度的动态响应模型，并通过一维搜索分离出刀具偏心跳动，再次建立偏心跳动-瞬时铣削力模型与偏心跳动-瞬时铣削厚度模型，完成刀具偏心跳动参数辨识，最终通过铣削试验平台验证模型合理性。

1 刀具斜角切削时的铣削力与铣削厚度有限元模拟

基于平头立铣刀螺旋角的客观形态，高速铣削时每个铣削微元通常都被当作为斜角切削，在只考虑刀具旋转忽略进给速度情况下，将瞬时铣削力按笛卡尔坐标系分解成切向力Fx、径向力Fy、轴向力Fz三个分量。初设模拟条件如下：选用刀具为AL6061-T6平头立铣刀；刀具前角、后角、刃倾角分别为10°、9°、30°；切削速度为2000 mm/s；切削厚度为0.01～0.15 mm；刀具-切屑传热系数取值0.011 W/℃；工件材料热传导系数为180 W/(m·K)，环境温度设置为20°[4]。模拟结果如表1、图1所示。通过模拟发现铣削力变化主要分为切入、稳态、切出阶段，其中稳态阶段铣削力虽整体趋于平稳，但由于材料性能、刀具偏心跳动及摩擦接触等因素仍存在一定波动，其中轴向力波动最为明显。标准偏差表示为稳态阶段切削力数值分布的分散程度，即铣削力的波动幅度。标准偏差值越小，即模拟数据越接近于平均值。

图1 铣削力参数与切削厚度关系

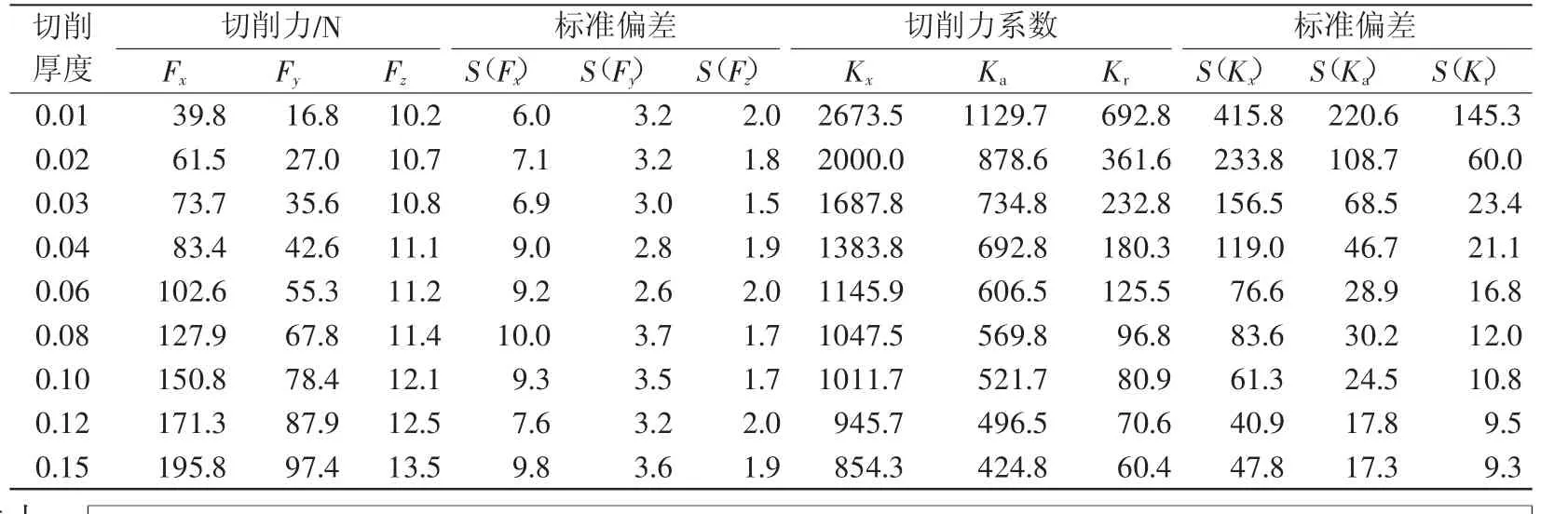
表1 平头立铣刀铣削模拟结果

由数据可知，切削厚度越大，切向力Fx、径向力Fy、轴向力Fz随之增大，其中，切削厚度为零但铣削力不为零现象主要由犁入效应造成。其中三分量中切向力变化最大，径向力最小，但均与切削厚度呈较为规则的线性关系。

根据Martellotti[5]提出的切削微元上切削力等于切削力系数乘以切削微元的面积，可将第i个刀齿上第j个切削微元的切向受力、径向受力与轴向受力表示为dFxi.j（φ）、dFzi.j（φ）、dFyi.j（φ）。

式中：Kx、Ky、Kz为切向、轴向与径向铣削力系数；N为刀具齿数；M为刀具齿数的微元数；hi.j(φ)为瞬时切削厚度；dz为切削微元的轴向高度；φ为立铣刀旋转角度。

用θi.j(φ)表示切削微元的瞬时角位移，fz为每齿的进给量，β表示刀具螺旋角，D为刀具直径。瞬时切削厚度与瞬时刀具角位移分别可以表示为：

2 刀具偏心跳动参数分离与有限元模拟

由于多种原因，刀具偏心跳动始终无法彻底避免，影响着铣削力的大小。因此，把刀具偏心跳动纳入铣削力预测的考虑范围显得尤为重要。为了反映切削力系数的尺寸效应，本文采用与瞬时未变形切削厚度成指数形式的瞬时切削力系数，且给出刀具偏心跳动参数的辨识步骤，将瞬时铣削力分为瞬时未变形切削厚度部分的铣削力（理想铣削力）与刀具偏心跳动引起的铣削力（刀偏铣削力）两大部分[7]。根据切削厚度的指数函数，将理想铣削力表示为

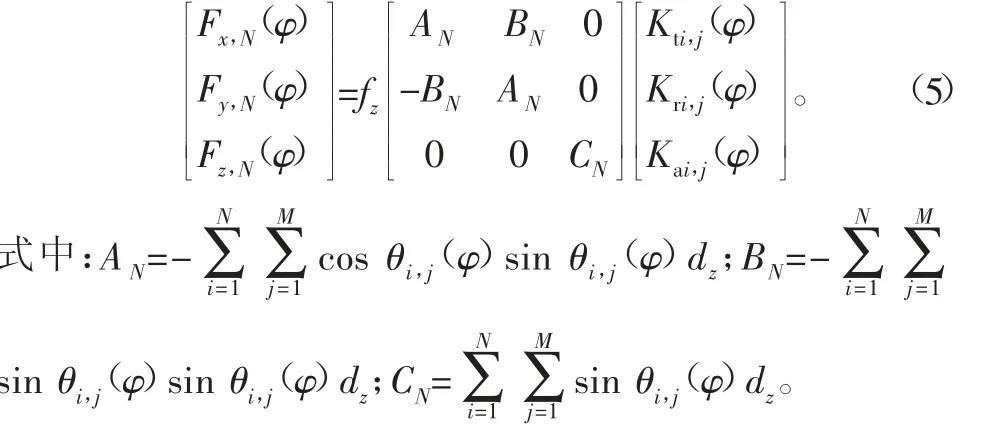
其中刀具偏心跳动可通过有限元模拟后的铣削力系数求取实测值与预测值之差的平方和来分离出刀具偏心跳动的数学模型。设定步长初始值ρ=0，λ=0，根据瞬时未变形切削后的近似表达式与瞬时铣削力模型计算出3个矢量上的铣削力。设置实时步长ρ=ρ+Δρ，引入偏心跳动，利用铣削力分解公式计算出各位置角实测铣削力与预测铣削力，由此分离出偏心跳动，具体步骤如图2所示。

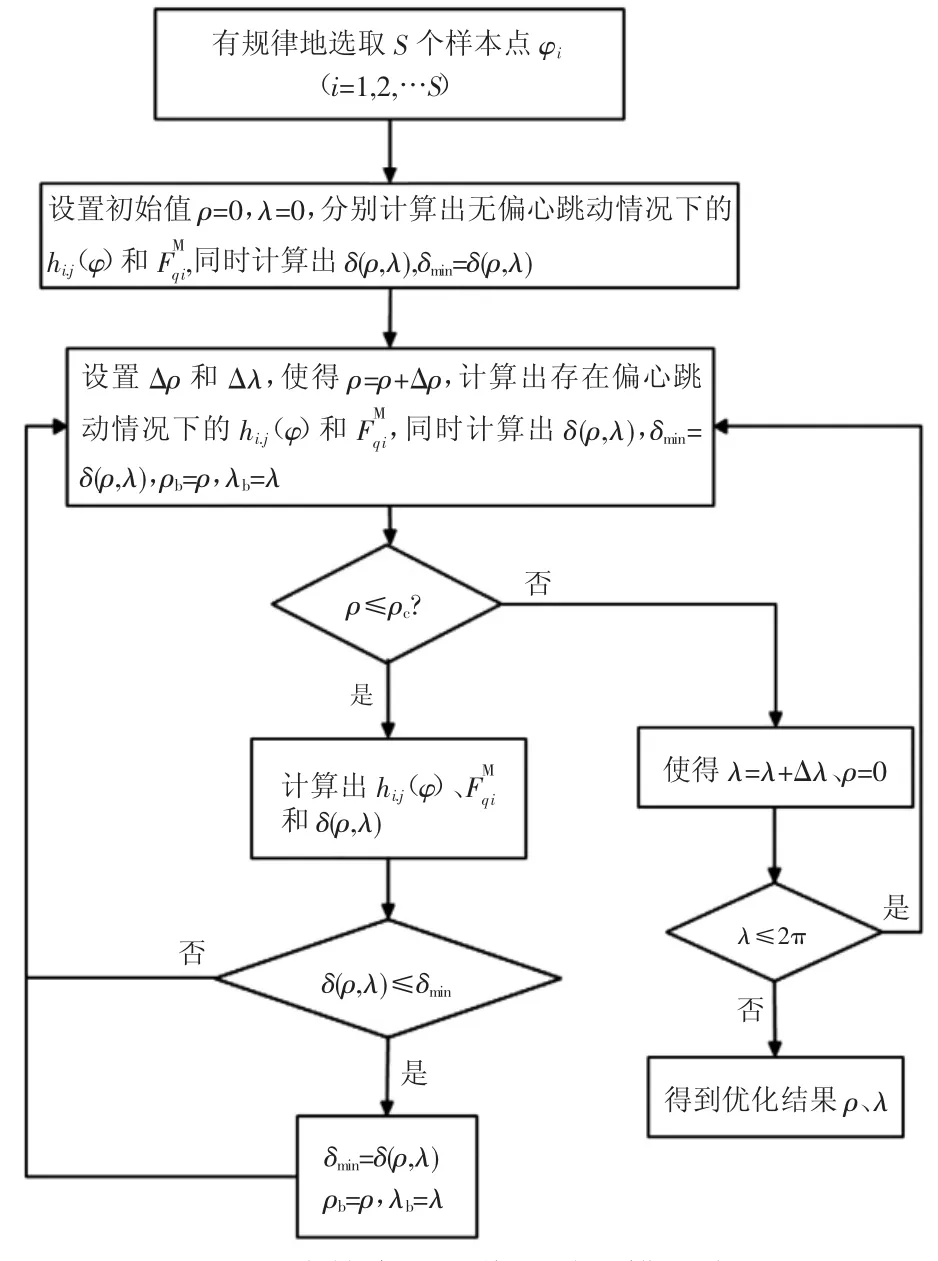
图2 一维搜索刀具偏心跳动辨识流程

分离后刀具偏心跳动引起的铣削力则可表示如下：

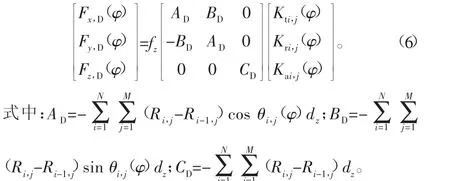
3 考虑刀具偏心跳动的铣削力有限元模拟

接下来，利用刀具实体模型再次采用DEFORM-3D有限元软件模拟引入刀具偏心跳动因素的铣削力变化实体旋转角度达290°～315°之间时，铣削力最大，此时铣削状态呈稳态中刀具旋转最大值，随后进入切出状态，铣削力急速下降。由此获悉，利用有限元模拟方式分离刀具偏心跳动在理论上可行。

4 刀具偏心跳动试验论证

铣削试验过程中，刀具参数不变，保持加工过程处于稳定状态，合理选择铣削速度、每齿进给量、轴向切深和径向切深进行试验。试验条件如表2所示。

表2 试验条件

通过DEWESOFT-6-SE分析软件，得到试验中铣削参数对应的铣削力。对获得的实验数据进行适当的处理，最后选取刀具旋转一周内的数据进行分析研究。在进行铣削参数辨识时，需要瞬时未变形切削厚度与旋转角度一一对应，否则影响铣削参数辨识的正确性，因此，需要对所得到的铣削力进行同步处理，从所得数据中任意提取10个连续周期的铣削力数值，编写MATLAB程序，求取10个周期内的铣削力平均值，把10个周期内的铣削力平均值与模拟出的铣削力进行对比，调整平均铣削力，得到与旋转角度具有对应关系的一组铣削力。最终获得铣削力曲线，如图4、图5所示。

由图4、图5可知，考虑了刀具偏心跳动的铣削力曲线与有限元模拟铣削力预测曲线具有较好的一致性，由此可以验证由有限元模拟得出的铣削力模型及由刀具偏心跳动引起的铣削力模型可以作为铣削力力学分析与机床过程，鉴于刀具径向受力微弱，对铣削加工影响较小，模拟中仅考虑切向铣削力与轴向铣削力[8]。铣削参数同为fz=0.04，n=4000 r/min，ap=1 mm，ae=1 mm。以特征最为明显的X方向铣削力为例，如图3所示。

图3 切向铣削力Fx 有限元模拟结果

图4 实测与预测切向铣削力试验曲线（无偏心跳动）

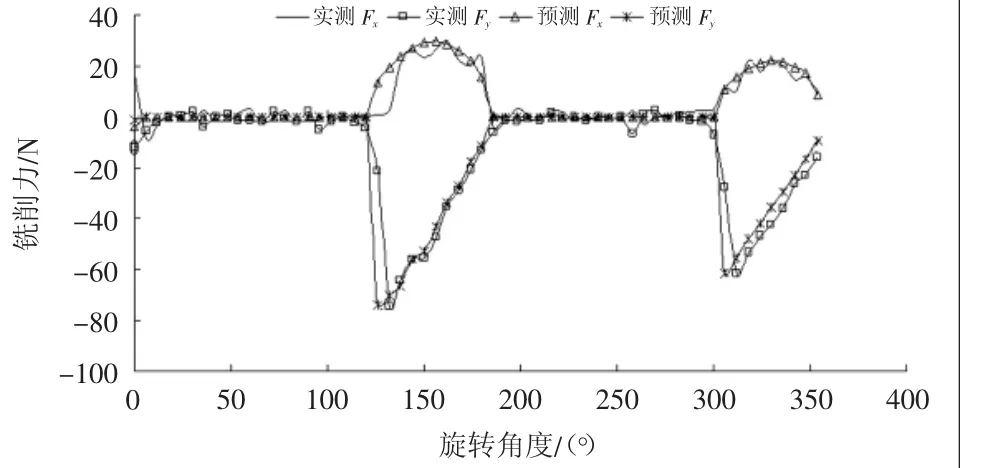
图5 实测与预测铣削力试验曲线（包含偏心跳动）

由模拟结果获悉，在试验值、斜角切削与刀具实体3种状态中，斜角切削铣削力曲线最为平滑，主要原因即是未考虑铣削时的刀具偏心跳动。而考虑了刀具偏心跳动的刀具实体铣削力曲线与试验值，其曲线波动明显增大，幅值呈上升趋势。当刀具加工稳定性研究的参考。

5 结语

本文以DEFORM-3D有限元软件模拟高速铣削时瞬时铣削力变化，根据铣削力与铣削厚度的线性关系以及回归方程建立铣削力模型，并通过一维搜索分离出刀具偏心跳动引起的铣削力变化模型，再次运用有限元软件模拟考虑了刀具偏心跳动的铣削力变化过程，并最终通过数控试验平台验证刀具偏心跳动实测与预测的一致性，验证刀具偏心跳动模型的正确性，为后期铣削参数的优化奠定基础。