抗蛇行减振器动态模型对高速列车横向平稳性影响*

池长欣，梁树林，池茂儒，高红星，李奕潇

（西南交通大学 牵引动力国家重点实验室，成都 610031）

良好的运行平稳性能够确保旅客乘坐舒适度，是高速列车的重要动力学性能之一。动车组高速运行时，转向架产生的剧烈蛇行运动会对运行平稳性和行车安全性造成很大的影响，有时甚至会破坏线路，引起车辆脱轨事故。为了控制车辆系统的蛇行运动，通常在车体和转向架之间设置合理的抗蛇行减振器，它通过增加车体和转向架之间的回转阻尼力矩来抑制和控制车体或转向架蛇行运动，从而有效改善了车辆横向平稳性和运动稳定性。因此，抗蛇行减振器成为了高速动车组最重要的悬挂元件之一［1-2］。

文献［3-6］通过传统车辆动力学仿真分析的方法研究了抗蛇行减振器阻尼特性对车辆动力学性能的影响规律，但均是使用分段线性模型来表示抗蛇行减振器的阻尼特性，虽然可以兼顾减振器卸荷前和卸荷后2种不同的阻尼特性，但它计算的阻尼力始终随激励速度大小的增加而线性增加，难以体现减振器的非线性动态特性，无法满足高速列车动力学仿真精度需求，故有必要开展抗蛇行减振器动态模型的研究。

文献［7］通过试验分析的方法对传统的抗蛇行减振器模型进行了修正，使其更接近试验结果；文献［8］通过考虑抗蛇行减振器的串联刚度、结构阻尼和安装间隙，建立了一种更精细的抗蛇行减振器模型；文献［9］基于抗蛇行减振器物理参数，建立了抗蛇行减振器的物理参数模型，该模型能较好体现抗蛇行减振器的动态特性。文献［10］结合台架试验研究了抗蛇行减振器内部结构对其动态刚度的影响规律。以上研究多为抗蛇行减振器动态模型的研究，但基于抗蛇行减振器动态模型对车辆动力学性能的影响研究尚且较少。此外，据某型动车组动力学线路跟踪试验反馈，当踏面等效锥度低于0.023时，列车在某个低速区间易出现异常的横向晃动现象，导致车辆横向平稳性急剧降低，当列车提速至正常运行速度后，这种异常横向晃动也随之消失。传统动力学仿真模型难以重现该异常现象，故文中结合抗蛇行减振器工作机理，建立一种高精度的抗蛇行减振器动态模型，并将其与传统动力学模型进行联合仿真，以研究抗蛇行减振器动态模型对高速列车横向平稳性的影响。

1 模型建立

抗蛇行减振器物理结构如图1所示［11］，抗蛇行减振器动态模型建立的主要工作是分析各部件流量的压力—流量特性。建模工作主要包括压力腔（拉伸腔、压缩腔）建模、常通孔建模，阻尼阀（回油阀、卸荷阀）建模，储油缸建模。

图1 抗蛇行减振器物理结构简图

1.1 压力腔模型

压力腔模即建立压力腔内各状态变量的微分形式，可表示为式（1）：

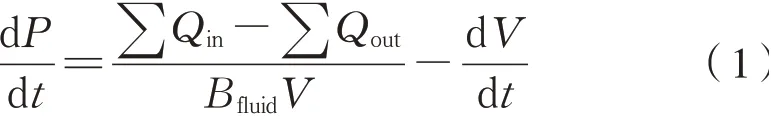
式中：V为油液体积；Bfluid为压力腔混合液体（油液和空气）的体积弹性模量；P为压力腔内油液压强；Qin为流入腔体的体积流量；Qout为从腔体流出的体积流量。

1.2 常通孔模型

常通孔模型建模的关键是计算不同压力差下流过常通孔的流量Q以及流量系数的确定，若不考虑其流量损失，由伯努利方程即可获得常通孔的压力—流量特性，为式（2）：

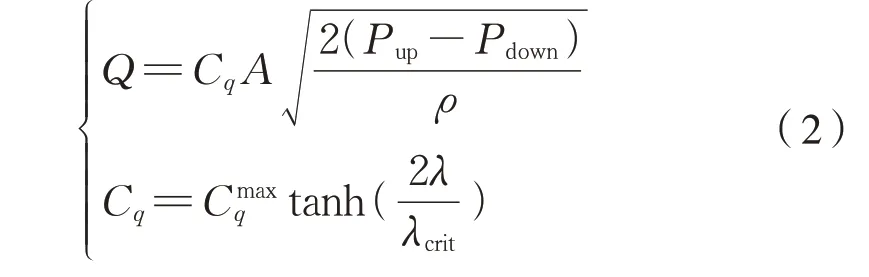
式中：A为常通孔面积；Cq为流量系数为最大流量系数，通常取0.7；λ是流动数；λcrit是临界流动数，与常通孔结构有关；ρ为腔体内油液密度。

1.3 阻尼阀模型

阻尼阀（卸荷阀、回油阀）建模主要是通过阀系元件运动方程和伯努利方程建立其对应的压力—流量方程，文献［11］已详细描述了阻尼阀和卸荷阀的具体建模方法。

1.4 储油腔模型

储油腔内存在一定量的气体，假设其气体体积增加量等于油液体积减少量，结合理想气体状态方程即可推导出气体压力的微分表达式（3）［11］：式中：γ为气体多变系数，绝热状态下取1.4。

1.5 抗蛇行减振器动态模型

利用各部件流量相等原则即可完成各子模型之间的衔接，通过压力腔的压力值即可表示抗蛇行减振器的动态阻尼力，为式（4）：

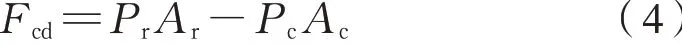
式中：Fcd为抗蛇行减振器动态阻尼力；Pr为拉伸腔压力；Pc为压缩腔压力；Ar为拉伸腔侧活塞面积；Ac为压缩腔侧活塞面积。

利用Simulink仿真软件搭建上述抗蛇行减振器动态模型并对其进行仿真，如图2所示。

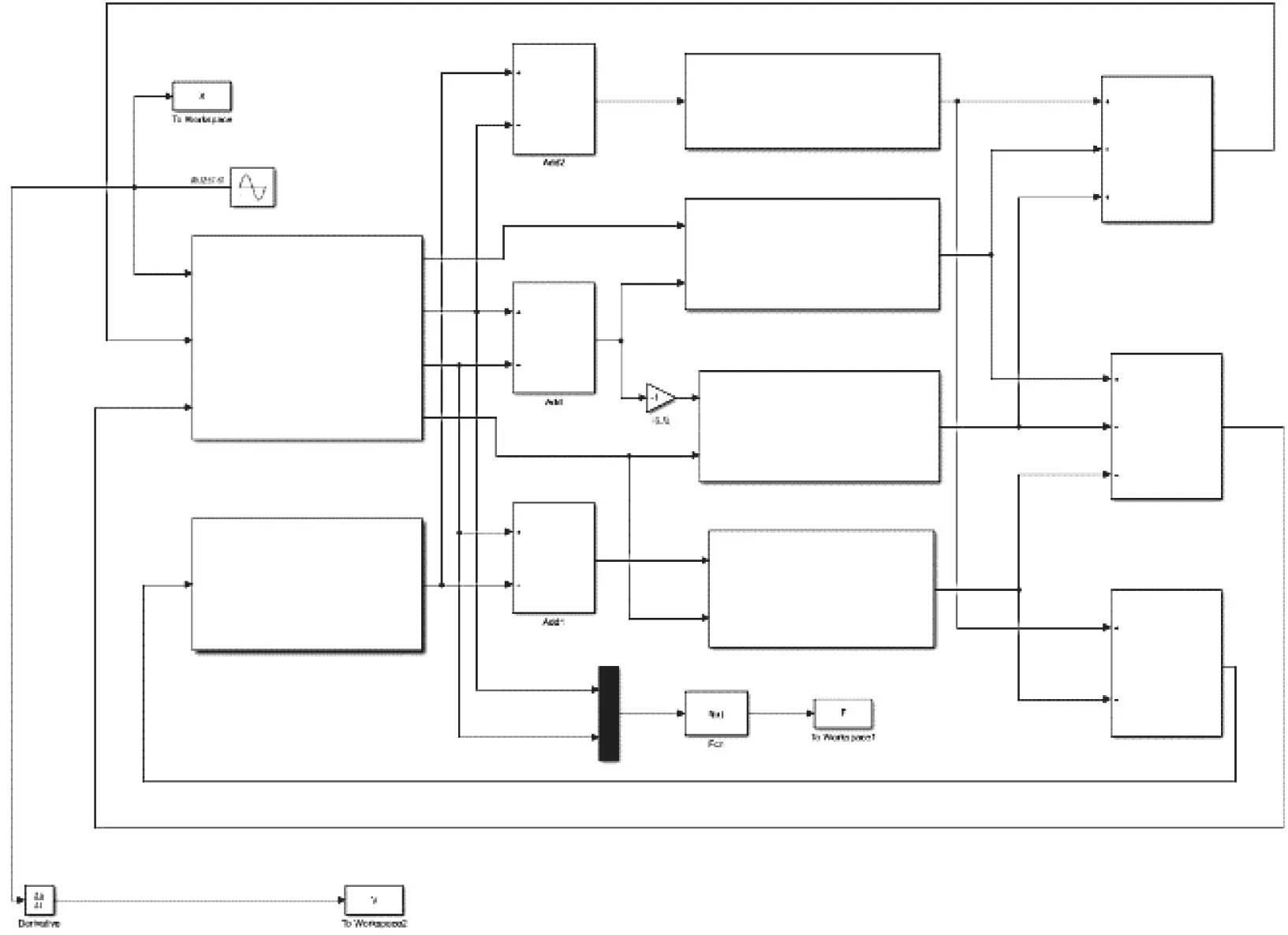
图2 抗蛇行减振器动态模型

1.6 抗蛇行减振器分段线性模型

抗蛇行减振器分段线性模型通常是以抗蛇行减振器卸荷速度作为分界点，用2个不同的线性阻尼系数来表示不同速度区间的阻尼特性，为式（5）：

式中：v为减振器两端激励速度；Vd为抗蛇行减振器卸荷速度；C1为抗蛇行减振器卸荷前阻尼系数；C2为抗蛇行减振器卸荷后阻尼系数。

2 抗蛇行减振器动态试验

2.1 试验设备

西南交大牵引动力国家重点实验室的悬挂元件性能测试试验台，如图3所示，抗蛇行减振器装于该试验台后，可通过试验台两端的内置油缸实现液压锁紧。

图3 悬挂元件性能测试试验台SPTB-100

2.2 试验方法

该次试验对象采用的是某型高速动车组抗蛇行减振器，试验方法参考标准《EN 13802-2013 Railway application-suspension components-hydraulic damper》［12］和《TB/T 1491-2015机 车 车 辆 油 压 减振器技术条件》［13］。激励采用的是位移控制下的正弦扫频激励，激励的幅值范围为0.5~1 mm，频率范围为0.25~10 Hz。所有的试验结果均是在不带橡胶节点的情况下测得，从而消除橡胶节点对子模型的影响。因此，下文重点对比不带橡胶节点的减振器仿真计算和试验的示功图。

3 抗蛇行减振器动态模型仿真与试验对比

采取与试验工况一致的正弦激励，对所建模型进行仿真计算。示功图是反映减振器行为过程的主要手段，为对比方便，将仿真计算示功图与试验示功图放在同一图中。抗蛇行减振器在激励幅值为0.5 mm、频率为0.25~10 Hz动态工况下的仿真结果与试验结果对比如图4所示，抗蛇行减振器在激励幅值为1 mm、频率为0.25~10 Hz动态工况下的仿真结果与试验结果对比如图5所示，从图中可以看出抗蛇行减振器动态模型的仿真结果与试验结果吻合较好；分段线性模型与试验结果吻合较差。其原因是减振器腔体中油液在高频动态工况下会被短暂压缩而无法及时释放，形成了一定大小的回复力，此时减振器的阻尼力除了黏性阻尼力外，还存在因油液被压缩而产生的回复力。分段线性模型只体现了油液的黏性阻尼力，其数值随着激励速度增大而线性增大，并在激励速度最大的时候达到最大值，激励速度最小时达到最小值，不能描述油液动态工况下被压缩的过程，故仿真所得的示功图与试验结果相差较大。抗蛇行减振器动态模型建模时重点考虑了油液的可压缩特性，对油液的弹性模量、密度等参数的动态变化过程进行了详细建模，所以计算的示功图能与试验结果很好吻合，能够体现抗蛇行减振器动态工况下的非线性动态特性。

图4 在不同激励频率下抗蛇行减振器动态模型的仿真结果与试验结果对比（幅值0.5 mm）

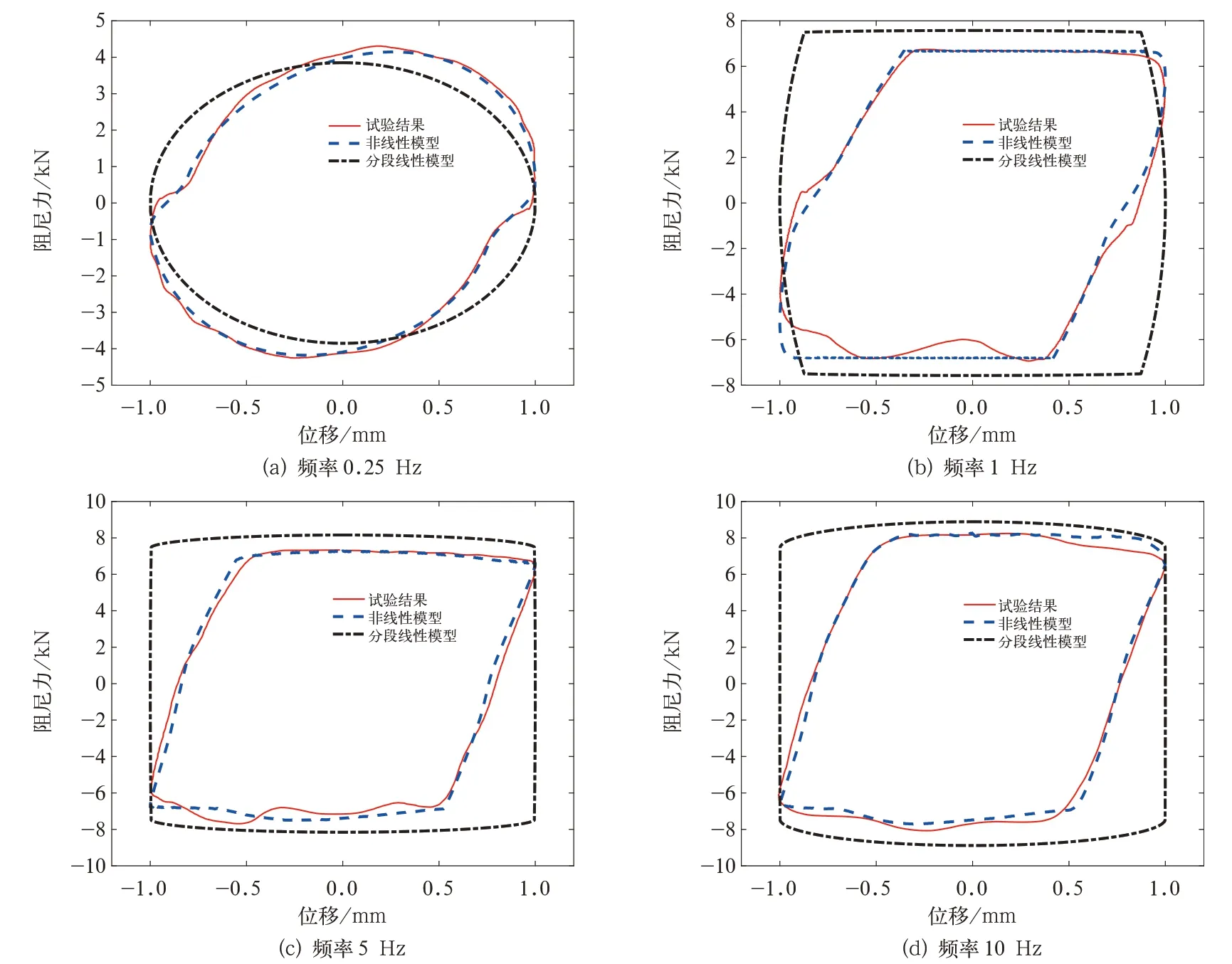
图5 在不同激励频率下抗蛇行减振器动态模型仿真结果与试验结果对比（幅值1 mm）

4 抗蛇行减振器动态模型对高速列车横向平稳性的影响分析

通过使用Simpack动力学仿真软件的SIMAT接口，将Simulink仿真软件搭建的抗蛇行减振器动态模型与某型高速列车动力学模型进行联合仿真，对高速列车的横向平稳性展开分析。

4.1 横向平稳性

导入某线路实测轨道谱，对联合仿真模型和传统动力学模型的横向平稳性进行研究。仿真工况为直线工况，轨道谱最大波长为50 m，平稳性指标计算方法参考标准《GB∕T 5599—2019机车车辆动力学性能评定及试验鉴定规范》［14］。车辆横向平稳性随行车速度和等效锥度的变化规律如图6所示。

分析图6可知，传统动力学模型在等效锥度为0.01~0.09范围内，计算的横向平稳性指标值一直随速度的增加而增加。联合仿真模型在等效锥度为0.03~0.09范围内，计算的横向平稳性指标值一直随速度的增加而增加；在等效锥度为0.01时，计算的横向平稳性指标值在100~350 km/h速度区间内会随速度的增加先增加后减小，这种变化规律与高速列车异常横向晃动出现的规律类似，为了进一步研究这种异常现象，对该速度区间下的车体横向振动加速度频域信号进行分析。

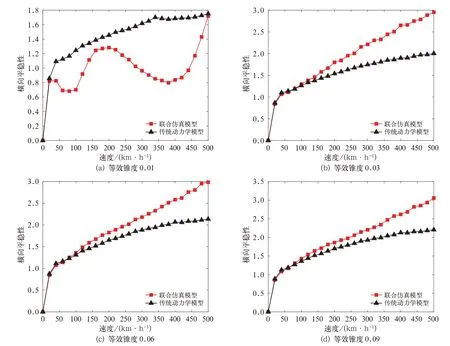
图6 车辆横向平稳性仿真计算结果

4.2 加速度频谱

联合仿真模型在等效锥度为0.01时的横向振动加速度频谱图如图7所示，车体悬挂振动模态的5种固有振动的自振频率见表1，基本不随车辆运行速度的变化而变化。

表1 自振频率 单位：Hz

分析图7可知，速度为100 km/h时，横向振动加速度的振动能量分散在0~25 Hz频率之间，最大振幅不超过0.004 5 m/s²；当速度增至200 km/h，横向振动加速度振动能量分布集中在0.56 Hz的单一频率上，且最大振动幅值急剧增大，达到了0.075 4 m/s²；当速度增至250 km/h，横向振动加速度振动能量分布集中在0.59 Hz的单一频率上，但最大振动幅值下降至0.053 1 m/s²；当速度增至350 km/h，横向振动加速度振动能量分散在0~25 Hz频率之间，最大振幅急剧下降，且不超过0.016 m/s²。结合表1可知，造成该异常横向振动的原因应该是车体蛇行运动频率在列车速度为200 km/h附近时与车体下心滚摆频率发生耦合，导致横向振动能量急剧增大，使得横向平稳性急剧恶化。当行车速度逐渐大于200 km/h时，车体蛇行运动频率也逐渐升高并远离车体下心滚摆频率，因此横向振动能量也大幅度降低，横向平稳性也得到极大改善。联合仿真模型很好地重现并解释了高速列车低等效锥度下的异常横向振动现象；图7仿真结果表明，提高踏面等效锥度可以有效避免该异常振动发生，与动力学线路跟踪试验统计规律一致。因此，抗蛇行减振器动态模型有效提高了动力学仿真精度，能够准确地反映横向振动加速度变化规律，为研究高速列车动态特性提供了良好的理论基础。

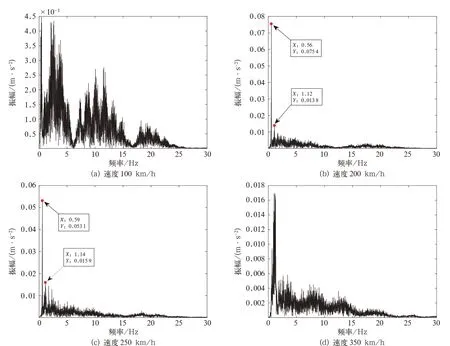
图7 联合仿真模型横向振动加速度频谱图（等效锥度0.01）

5 结论

抗蛇行减振器动态模型基于其内部结构工作原理，对油液理化属性动态变化过程进行了详细建模，仿真结果与试验结果基本一致，能够准确描述抗蛇行减振器动态工况下的非线性动态特性。

抗蛇行减振器动态模型与动力学联合仿真模型能够在低等效锥度、低运行速度环境下，重现车体蛇行运动频率与车体下心滚摆频率耦合现象，解释了高速列车车体异常横向晃动现象。表明抗蛇行减振器动态模型能有效提高动力学仿真精度，能够准确反映车体蛇行运动频率对车体横向振动加速度的影响关系，为研究高速列车横向平稳性变化规律提供了良好的理论平台。