三轴线运输车连杆转向机构动力学建模与参数辨识*

杨飞雪，康绍鹏，强红宾，刘凯磊，吴 昊

（江苏理工学院机械工程学院，江苏 常州 213001）

目前，常用的多刚体系统动力学的建模方法主要有牛顿-欧拉法、拉格朗日方程法以及凯恩法[1-3]。而参数辨识主要有最小二乘法[4]、神经网络法、遗传算法等。牛顿-欧拉法原理明朗并且能够较为清晰地描述三轴线连杆转向机构，而最小二乘法能够较为简便地求得未知数据，所以文中采用牛顿-欧拉法对三轴线运输车连杆转向机构进行动力学建模[5-6]，采用最小二乘法对三轴线运输车连杆转向机构的动力学模型进行参数辨识。

1 连杆转向系统数学模型

1.1 数学建模原理

牛顿-欧拉法是多刚体动力学领域使用较为广泛的建模方法，它首先需要建立惯性坐标系和机体坐标系，再分别对多刚体系统的各个杆件进行受力分析，列写力和力矩方程，最后结合运动学方程得到完整的动力学模型。以下方程组（1）中两个等式分别为Newton和Euler方程：

式中，Joi是第i个杆件对质心的惯量张量，ωi和分别为第i个杆件的角速度和角加速度，voi是第i个杆件的质心速度，mi是第i个杆件的质量，αi是质心加速度，Fi和Mi分别为主矢和主矩。

1.2 动力学建模

如图1所示，三轴线连杆转向机构中每个轴线有八个轮胎，从左到右分别为第一轴线、第二轴线和第三轴线。其中，由铰接在车架上的液压缸的伸缩带动转向臂转动一定的角度，然后带动铰接在转向臂上的两个横拉杆运动，而横拉杆推动车轮上方的悬挂机构，悬挂机构带动轮胎的转动从而实现车轮按一定的角度进行转向。与此同时，转向臂的转动还会带动纵拉杆完成下一轴线的转向臂的转动，实现轴线车的整体转向[7]。

针对图1 建立第一轴线外侧的连杆转向[5]的动力学模型，如下所示。

图1 三轴线连杆转向图

式中：FE1X是车架施加在转向臂中心上的约束反力的x分量，FF1X是转向横拉杆施加在转向臂上的约束反力的x分量，mE1F1是转向臂的质量，FE1Y是车架施加在转向臂中心上的约束反力的y分量，FF1Y是转向横拉杆施加在转向臂上的约束反力的y分量，M1是转向臂的主动转向力矩，Jo1是主动杠的转动惯量。

2 参数辨识

2.1 动力学方程线性化

将式（2）、（3）、（4）所建立的三轴线运输车第一轴线外侧连杆转向机构动力学方程转化成如下数学表达式：

其中，A1表示一个信息矩阵，x1表示待辨识参数。

在公式（6）的矩阵中的元素如下所示：

同理，第一轴线内侧、第二轴线外侧和第二轴线内侧的数学模型可以表达为类似的数学表达式。四部分的数学表达式可以统一为公式（8）。

2.2 激励轨迹的选择与优化

轴线车只有在实际工作中才能进行参数辨识，也只有实际应用才有意义。因此，在进行参数辨识时，要事先设计让轴线车充分运动的激励轨迹，同时还要对轨迹进行优化，使激励轨迹在满足轴线车实际约束的同时，又能最大化地激发所有需要辨识的参数，减小误差。因此，在轴线车的动力学参数辨识过程中，目前常用的激励轨迹主要有多项式轨迹和周期性轨迹，多项式轨迹常用于轨迹简单、精度要求不是很高的机器人，而周期性轨迹常用于轨迹复杂且具有循环性，同时精度要求相对较高的机器人。因此，本文选择采用周期性轨迹规划，将周期性轨迹设计为正弦函数和余弦函数的组合形式，通过有限次的迭加构成，也就是数学中的傅里叶级数。轴线车第i个关节的角位移的轨迹，可以用以下形式表示：

其中，ωf是傅里叶级数的基频。傅里叶函数的周期为2π/ωf。每一个傅里叶级数包含2N＋1 个参数：an和bn（n＝1，…，N）是正弦和余弦函数的幅值，q0是机器人产生激励时的关节补偿。

对于一个不稳定的线性方程Ax＝b，系数矩阵A和右端b都会产生一个不受控制的误差，而矩阵A的条件数则反映了这个线性方程的性态。条件数越大，解的误差越大，方程组被认为是病态的；条件数越小，可以认为方程组是良态的；当条件数为1 时，认为方程组的状态最好。矩阵A的条件数定义为：

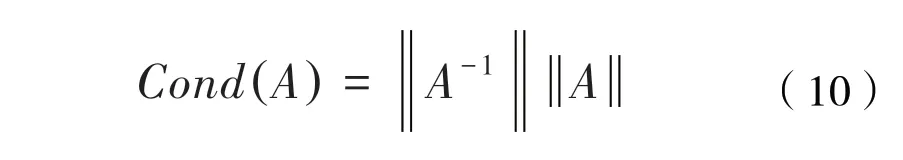
于是，确定优化激励轨迹的问题就变为确定系数（an、bn和q0）来使观测矩阵A的条件数最小。傅里叶函数中系数比较多，使用一般的试凑的方法计算量大并且很难得到准确值，因此必须选择某种优化算法进行参数选择。本文采用Matlab 中的fmincon 函数来确定激励轨迹参数。

在三轴线运输车连杆转向机构中转向臂中心会带动其余转向连杆进行相应的从动运动，所以只需要赋予转向臂中心一个激励轨迹。由式（9）可知，需要优化的参数是ai、bi（i＝1，…，N）和q0，其中N＝1，因此共有3个参数需要优化。

通过Matlab 中fmincon 函数并结合式（10）将激励轨迹的求解优化问题转化为以下的最值优化问题：

通过fmincon 函数求解出傅里叶级数参数，如表1所示。

表1 傅里叶级数最优激励轨迹优化后参数

得到激励轨迹如图2所示。

图2 傅里叶级数激励轨迹角度、角速度、角加速度

2.3 动力学参数辨识方法

针对动力学参数辨识，目前常用的方法主要有最小二乘法、神经网络法、遗传算法和极大似然估计法等。本文采用最小二乘法对已建立的动力学模型进行参数估计。

在Adams 与Simulink 的联合仿真中，让Adams 模型按照最优激励轨迹运行时，实时测量相应铰接点的转动以及相关铰接点的受力情况[8-9]，经过计算可以得到信息矩阵A和受力矩阵b。根据式（8）可以通过最小二乘法计算参数x的值，计算方法如式（12）所示。

2.4 三轴线运输车连杆转向机构参数辨识

通过Adams 与Simulink 的联合仿真将Adams 中的数据在Simulink 中通过最小二乘法进行处理可以得到三轴线连杆转向系统中各杆件的物理参数[10]。具体参数如表2所示。

表2 三轴线运输车连杆转向系统动力学辨识参数

3 结语

本文通过牛顿-欧拉法对三轴线运输车连杆转向机构进行了动力学建模并将动力学模型进行了线性化处理。在此基础上，选择傅里叶级数形式的函数作为参数辨识的激励轨迹并进行了最优化得到最优激励轨迹。最后，采用最小二乘法并通过Adams 与Simulink 的联合仿真，得到三轴线运输车连杆转向系统中各杆件的动力学参数。