Anisotropic flow in high baryon density region

Shao-Wei Lan· Shu-Su Shi

Abstract Collective flow is a powerful tool used to analyze the properties of a medium created during high-energy nuclear collisions.Here,we report a systematic study of the first two Fourier coefficients v1 and v2 of the proton and π+from Au＋Au collisions in the energy range =2.11-4.9 GeV within the framework of a hadronic transport model (UrQMD). Recent results from the STAR experiment were used to test the model calculations. A meanfield mode with strong repulsive interaction is needed to reproduce the 10-40% data at 3 GeV. This implies that hadronic interactions play an important role in the collective flow development in the high baryon density region.The mean values of the freeze-out time for protons and π+are shifted earlier owing to the additional repulsive interactions. We predict the energy dependence of the mean values of the transverse momentum 〈pT〉, v1, and v2 for both protons and π+ from the Au＋Au collisions.

Keywords Heavy-ion collisions · QCD phase diagram ·UrQMD · Collective flow · Mean-field potential

1 Introduction

The exploration of quantum chromodynamics (QCD)phase diagrams and nuclear matter properties has been one of the most important motivations for relativistic heavy-ion collisions [1-6]. The region of high temperature and vanishing baryon chemical potential of the QCD phase diagram, where the phase transition from hadronic matter to quark-gluon plasma (QGP) [7] is a smooth crossover, has been well studied in experiments at the RHIC [8-10] and LHC [11, 12]. Theoretical calculations suggest that there may exist a critical end point in the finite baryon chemical potential region [13]. It is well known that several observables,such as directed flow [14-17]and moments of distributions of conserved charges [18], have been proposed to be sensitive to critical behavior. In the RHIC Beam Energy Scan phase I program (BES-I), the nonmonotonic behavior of the net proton directed flow slope with respect to rapidity as a function of collision energy is observed,and the minimum of the distribution suggests the softest point of the equation of state(EoS)or prediction of the critical end point [19].

The collective flow [20, 21] has been extensively used to study the transverse properties of hot and dense matter created in heavy-ion collisions owing to their sensitivity to expansion dynamics. They are defined by the coefficients of the Fourier expansion of the azimuthal distribution of the emitted particles with respect to the reaction plane: [22]

2 The UrQMD model

3 Results and discussion

Fig. 1 (Color online) Reference multiplicity distribution in UrQMD with cascade mode in Au＋Au collisions at = 2.11-4.9 GeV.Similar to the experimental setup, the charged particles were measured within ｜η｜＜0.5

Fig. 2 (Color online) Rapidity dependence of v1 (top panel) and v2(bottom panel)of the proton and π+ in the 10-40%centrality Au＋Au collision at =3 GeV. The symbols denote STAR data.The red and blue bands represent the results from the UrQMD mean-field and cascade mode, respectively

Fig. 3 (Color online) Transverse momentum dependence of v1 (top panel) and v2 (bottom panel) of the proton and π+ in the 10-40%centrality Au＋Au collision at= 3 GeV. The symbols denote STAR data. The red and blue bands represent the results from the UrQMD mean-field and cascade mode, respectively

We systematically studied the mean-field potential effect on the particle production,directed flow,and elliptic flow development in the high baryon density region. The particle production yield as a function of kinetic freeze-out time for protons and π+in 3 GeV Au＋Au central collisions(0-10%) at mid-rapidity (｜y｜＜0.5) is presented in Fig. 4.The red and blue lines represent the results from the UrQMD mean-field and cascade modes,respectively.Note that these two distributions were normalized by the number of events. Overall, hadrons are produced mostly during kinetic freeze-out in the time interval 10-25 fm/c. The mean value of the distribution is shown in each panel using the corresponding colors.It can be seen that the mean value from the mean-field version is smaller than that of the cascade version. This can be explained by the larger pressure generated by the density-dependent fields, which drives the strong expansion. Thus, these hadrons are pushed outside the system and freeze out earlier than those from the cascade mode.

To quantify the strength of directed flow at mid-rapidity,a linear fit is employed to extract the slope of the v1（y）distribution [19,47],as shown in Fig. 2.The directed flow is exactly zero at y=0 owing to the momentum conservation effect. Figure 5 presents the v1slopes dv1/dy｜y=0and elliptic flow v2at mid-rapidity as a function of kinetic freeze-out time (t) for proton and π+in 3 GeV Au＋Au mid-central collisions (10-40%); the red and blue bands represent the results from the UrQMD mean-field and cascade mode,respectively. Both v1and v2are established in the very early stage of the system evolution and show a rapid increase for t ≾15 fm/c.They then increased slightly with increasing freeze-out time. As can be seen in the figure, the v1values for the mid-rapidity proton and pion start from below zero before turning into positive values at a later time, as experimentally observed. Owing to the baryonic mean field, at t ～15 fm/c, the v1slope for the proton is much larger than that of π+, especially in the results for the mean-field mode. Conversely, while the cascade predicts an in-plane expansion, for example, positive v2for both protons and pions, the mean field tends to keep the incoming nucleons together. As a result, shadowing seems to be sustained throughout the collision period, leading to negative values of v2and out-of-plane expansion at this energy.In short,compared to the cascade mode, the mean-field potential provides a stronger expansion in the x-z plane (v1) and an effective blocking that leads to the expansion in the y-z plane (v2) in Au＋Au collisions at 3 GeV.

Fig. 4 (Color online) Particle production yield as a function of freeze-out time for proton (left panel) and π+ (right panel) from UrQMD 3 GeV 0-10% Au＋Au collisions. The red and blue lines represent the results from the mean-field and cascade modes,respectively

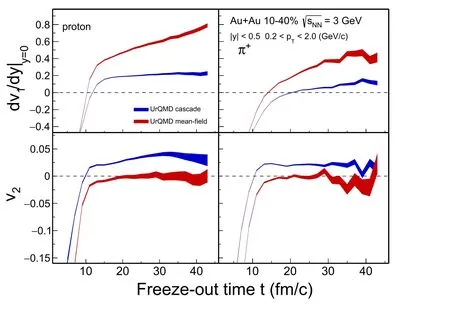
Fig.5 (Color online)v1 slopes(dv1/dy｜y=0)and v2 at mid-rapidity as a function of freeze-out time for proton (left panel) and π+ (right panel)from UrQMD 3 GeV 10-40%Au＋Au collisions. The red and blue bands represent the results from the mean-field and cascade modes, respectively

We will now discuss the energy dependence of directed and elliptic flows from UrQMD and compare this with world experimental data. Figure 7 shows the energy dependence of the mid-rapidity slope of directed flow(dv1/dy｜y=0) in 10-40% centrality Au＋Au collisions. The transverse momentum range in the UrQMD calculations for proton and π+is 0.4 ＜pT＜2.0 GeV/c and 0.2 ＜pT＜1.6 GeV/c, respectively, which is consistent with the STAR 3 GeV results [23]. The black symbols denote the world

Fig.6 (Color online)Mean transverse momentum〈pT〉as a function of collision energy for proton(squares)and π+(circles)from UrQMD 10-40% Au＋Au collisions. The red and blue symbols represent the results from the mean-field and cascade modes, respectively

4 Summary

Fig. 7 (Color online) v1 slopes (dv1/dy｜y=0) at mid-rapidity as a function of collision energy for proton (left panel) and π+ (right panel) from UrQMD 10-40% Au＋Au collisions. The red and blue symbols represent the results from the mean-field and cascade modes,respectively. World experimental data are represented by black symbols

Fig.8 (Color online)Similar to Fig. 7:v2 at mid-rapidity as a function of the collision energy for protons(left panel)and π+ (right panel)from UrQMD to 10-40% Au＋Au collisions

These results will be useful for understanding experimental data from upcoming experimental facilities focused on the high baryon density region.

AcknowledgementsThe authors thank Dr. J. Steinheimer and Dr.N. Xu for exciting discussions and the computing code.

Authors’ contributionsAll authors contributed to the study conception and design.Material preparation,data collection,and analysis were performed by Shao-Wei Lan and Shu-Su Shi. The first draft of the manuscript was written by Shao-Wei Lan, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

14. H.Sto¨cker,W.Greiner,High energy heavy ion collisions-probing the equation of state of highly excited hadronic matter.Phy.Rep.137, 277-392 (1986). https://doi.org/10.1016/0370-1573(86)90131-6

15. Y. Nara, H. Niemi, J. Steinheimer et al., Equation of state dependence of directed flow in a microscopic transport model.Phys. Lett. B 769, 543-548 (2017). https://doi.org/10.1016/j.physletb.2017.02.020

16. Y. Nara, H. Niemi, A. Ohnishi et al., Examination of directed flow as a signature of the softest point of the equation of state in QCD matter. Phys. Rev.C 94,034906 (2016).https://doi.org/10.1103/PhysRevC.94.034906

17. C.Zhang,J.Chen,X.Luo et al.,Beam energy dependence of the squeeze-out effect on the directed and elliptic flow in Au ＋Au collisions in the high baryon density region. Phys. Rev. C 97,064913 (2018). https://doi.org/10.1103/PhysRevC.97.064913

18. J.Adam,L.Adamczyk,J.R.Adams et al.,(STAR collaboration),nonmonotonic energy dependence of net-proton number fluctuations. Phys. Rev. Lett. 126, 092301 (2021). https://doi.org/10.1103/PhysRevLett.126.092301

19. L. Adamczyk, J.K. Adkins, G. Agakishiev et al., (STAR collaboration), beam-energy dependence of the directed flow of protons, antiprotons, and Pions in Au＋Au collisions. Phys. Rev.Lett. 112, 162301 (2014). https://doi.org/10.1103/PhysRevLett.112.162301 20. H. Sorge, Elliptical flow: a signature for early pressure in ultrarelativistic nucleus-nucleus collisions. Phys. Rev. Lett. 78, 2309(1997). https://doi.org/10.1103/PhysRevLett.78.2309

21. J.-Y.Ollitrault,Anisotropy as a signature of transverse collective flow. Phys. Rev. D 46, 229 (1992). https://doi.org/10.1103/Phys RevD.46.229

22. A.M. Poskanzer, S.A. Voloshin, Methods for analyzing anisotropic flow in relativistic nuclear collisions. Phys. Rev. C 58,1671 (1998). https://doi.org/10.1103/PhysRevC.58.1671

25. J. Cleymans, H. Oeschler, K. Redlich et al., Comparison of chemical freeze-out criteria in heavy-ion collisions.Phys.Rev.C 73, 034905 (2006). https://doi.org/10.1103/PhysRevC.73.034905 26. STAR Note 0598: BES-II whitepaper: studying the phase diagram of QCD matter at RHIC. http://drupal.star.bnl.gov/STAR/starnotes/public/sn0598

27. T. Ablyazimov, A. Abuhoza, R.P. Adak et al., (CBM collaboration), challenges in QCD matter physics -the scientific programme of the compressed baryonic matter experiment at FAIR.Eur.Phys.J.A 53,60(2017).https://doi.org/10.1140/epja/i2017-12248-y

28. V.Kekelidze,A.Kovalenko,R.Lednicky et al.,Prospects for the dense baryonic matter research at NICA. Nucl. Phys. A 956,846-849 (2016). https://doi.org/10.1016/j.nuclphysa.2016.03.019

29. J.C. Yang, J.W. Xia, G.Q. Xiao et al., High intensity heavy ion accelerator facility(HIAF)in China.Nucl.Instrum.Meth.B 317,263-265 (2013). https://doi.org/10.1016/j.nimb.2013.08.046

30. L.Lyu,H.Yi,L.M.Duan et al.,Simulation and prototype testing of multi-wire drift chamber arrays for the CEE. Nucl. Sci. Tech.31, 11 (2020). https://doi.org/10.1007/s41365-019-0716-x

31. S.A. Bass, M. Belkacem, M. Brandstetter et al., Microscopic models for ultrarelativistic heavy ion collisions.Prog.Part.Nucl.Phys. 41, 255 (1998). https://doi.org/10.1016/S0146-6410(98)00058-1

32. M. Bleicher, E. Zabrodin, C. Spieles et al., Relativistic hadronhadron collisions in the ultra-relativistic quantum molecular dynamics model. J. Phys. G 25, 1859 (1999). https://doi.org/10.1088/0954-3899/25/9/308

33. Y. Gao, F. Liu, A.H. Tang, Directed flow of transported and nontransported protons in Au ＋Au collisions from an ultrarelativistic quantum molecular dynamics model. Phys. Rev. C 86,044901 (2012). https://doi.org/10.1103/PhysRevC.86.044901

34. E.L. Bratkovskaya, M. Bleicher, M. Reiter et al., Strangeness dynamics and transverse pressure in relativistic nucleus-nucleus collisions. Phys. Rev. C 69, 054907 (2004). https://doi.org/10.1103/PhysRevC.69.054907

35. J. J. Molitoris, H. Sto¨cker, Further evidence for a stiff nuclear equation of state from a transverse-momentum analysis of Ar(1800 MeV/nucleon) ＋KCl. Phys. Rev. C 32, 346 (1985).https://doi.org/10.1103/PhysRevC.32.346

36. H. Kruse, B.V. Jacak, H. Stoecker, Microscopic theory of pion production and sidewards flow in heavy-ion collisions.Phys.Rev.Lett. 54,289 (1985). https://doi.org/10.1103/PhysRevLett.54.289 37. A.B. Larionov, W. Cassing, C. Greiner et al., Squeeze-out of nuclear matter in peripheral heavy-ion collisions and momentumdependent effective interactions.Phys.Rev.C 62,064611(2000).https://doi.org/10.1103/PhysRevC.62.064611

38. P. Hillmann, J. Steinheimer, M. Bleicher, Directed, elliptic and triangular flow of protons in Au＋Au reactions at 1.23 A GeV: a theoretical analysis of the recent HADES data. J. Phys. G 45,085101 (2018). https://doi.org/10.1088/1361-6471/aac96f

39. Y.J.Wang,C.C.Guo,Q.F.Li et al.,Determination of the nuclear incompressibility from the rapidity-dependent elliptic flow in heavy-ion collisions at beam energies 0.4A-1.0A GeV. Phys.Lett. B 778, 207-212 (2018). https://doi.org/10.1016/j.physletb.2018.01.035

42. C. Sturm, I. Bo¨ttcher, M. De¸bowski et al., Evidence for a soft nuclear equation-of-state from kaon production in heavy-ion collisions.Phys.Rev.Lett.86,39(2001).https://doi.org/10.1103/PhysRevLett.86.39

43. Ch. Hartnack, H. Oeschler, J. Aichelin, Hadronic matter is soft.Phys. Rev. Lett. 96, 012302 (2006). https://doi.org/10.1103/PhysRevLett.96.012302

44. Z. Feng, Constraining the high-density behavior of nuclear equation of state from strangeness production in heavy-ion collisions. Phys. Rev. C 83, 067604 (2011). https://doi.org/10.1103/PhysRevC.83.067604

47. L. Adamczyk, J.R. Adams, J.K. Adkins et al., (STAR Collaboration), Beam-energy dependence of directed flow of