分数阶双稳系统随机共振现象研究及FPGA实现

竺 佐， 郑永军， 罗 哉

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

1 引 言

在微弱信号检测中，有用信号往往被噪声所淹没[1～3]。传统的微弱信号提取方法是滤除噪声，即通过构造合适的滤波器让含噪信号中的噪声被滤除而有用信号得到保留。但在一定条件下，噪声也能产生促进作用，如随机共振。

随机共振是通过加入适度的噪声，令待提取微弱信号和噪声在非线性系统中发生“协作”效果，从而使得噪声可以发挥积极作用，增强系统信噪比[4～6]。迄今，研究者对随机共振现象进行了广泛的研究，但大部分基于整数阶模型。但在一些实际复杂系统中，系统的当前状态往往与其过去状态息息相关，具有记忆依赖性。而分数阶微积分能够通过加权表示来累积函数一段范围内的整体信息[7]。因为这一特性使得分数阶系统对一些具有记忆依赖性以及空间相关性的复杂系统的描述比整数阶系统更精确、简明，并且在信噪比增益等方面，分数阶随机共振系统的优势尽显无疑[8,9]。目前为止，分数阶随机共振尚处于起步阶段，文献[10]通过改进Oustaloup算法对分数阶郎之万方程求解，并搭建了分数阶随机共振仿真模型。文献[11]提出在合适的参数下，线性过阻尼Langevin方程可产生随机共振现象。然而，上述文献仅停留在理论推导和仿真阶段，对其在实际工程中的应用鲜有涉及，故开发一种分数阶随机共振的硬件系统具有十分重要的工程应用价值。现场可编程阵列(FPGA)具有计算能力强，并行处理等优势，非常适合在传统微处理器不能提供足够的速度和设计灵活性的情况下实现分数阶系统。分数阶系统硬件实现的难点在于分数阶微积分算子具有内存依赖性，需要大量的硬件资源。近年来，Muresan C I等提出一种基于FPGA的直流电动机分数阶控制器的硬件实现算法[12]，Adams等提出一种利用高阶有限冲激响应滤波器或一阶无限冲激响应之和的方法在FPGA上实现分数阶系统[13]。然而，上述大多数分数阶系统的硬件实现都针对特定系统，改变分数阶值或离散化步长都需调整代码，且其实现方法都较为复杂并未对硬件资源进行优化。

综上所述，本文以广义郎之万方程为理论基础结合分数阶微积分定义，将其推广至双稳态的分数阶郎之万方程，同时介绍了一种分数阶双稳随机共振系统的FPGA实现方法，并且对其进行实验仿真，验证了在适当分数阶阶数范围内，系统信噪比得到增强，出现了随机共振现象。

2 分数阶双稳态随机共振系统

2.1 随机共振基本原理

随机共振现象主要描述了在合适的条件下，驱动力(微弱有用信号)、随机力和非线性系统可发生“协作”效果，致使无序的噪声产生有利作用，增强微弱有用信号的现象[14]。

郎之万方程可用来表示经典的随机共振模型：

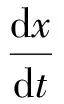
(1)

式中：x为粒子的运动轨迹；A0cos(2 πft+φ)是外界作用到双稳态系统的弱周期驱动力，其中A0为信号幅值，f为调制信号频率；ζ(t)是高斯白噪声，其满足自相关函数〈ζ(t)ζ(0)〉=2Dδ(t)；U(x)为式(2)所示的双稳态势场函数：

(2)

式中：a∈R+、b∈R+是双稳态系统结构参数，通过调整a，b的值，可得到不同形状的双稳态势阱。

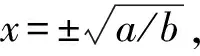
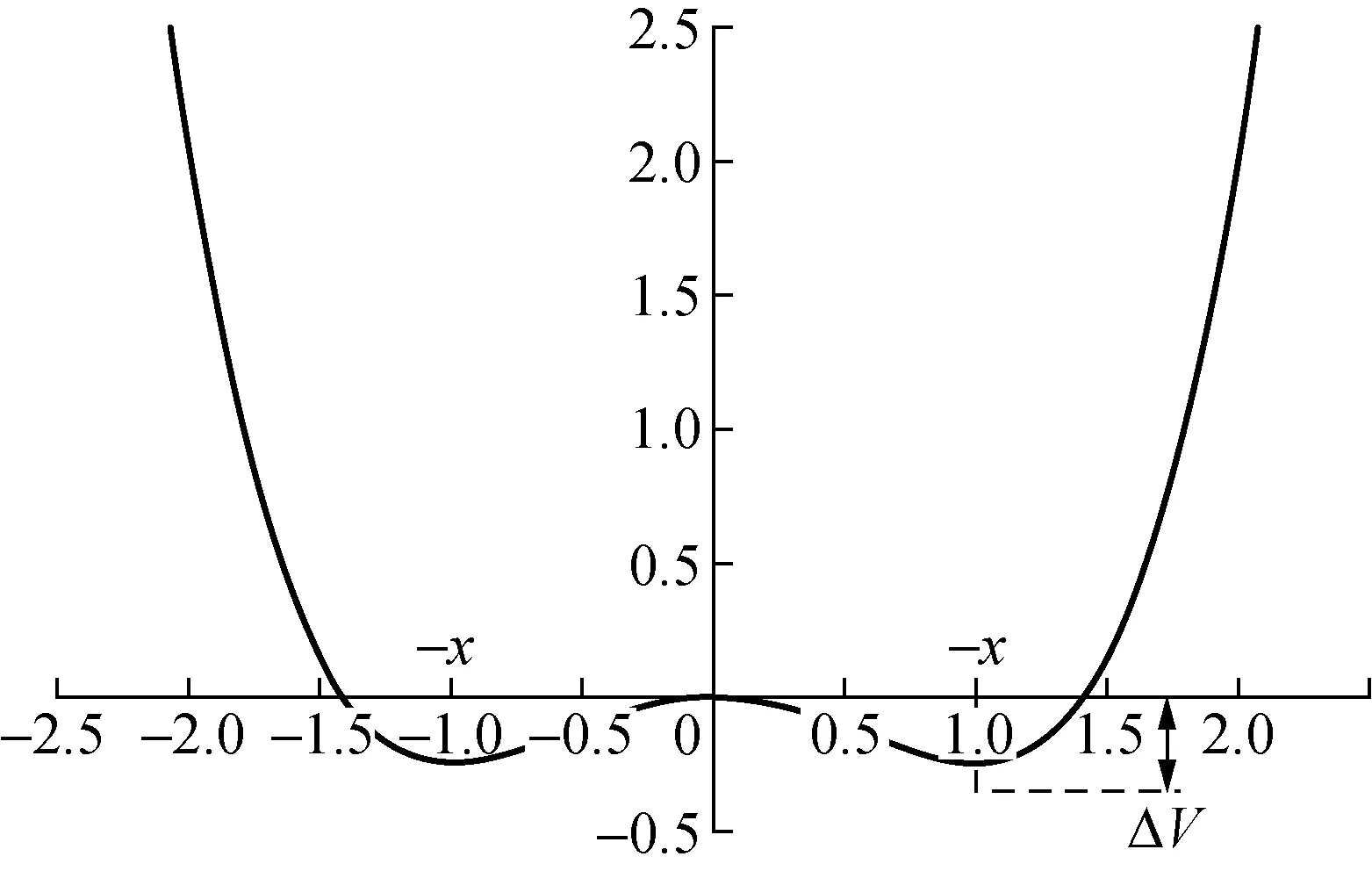
图1 双稳系统势函数

当系统的初始状态x>0或x<0时，布朗粒子最终会趋于稳定于两个势阱的其中一个势阱，且布朗粒子要离开此势阱到另一个势阱需要外力触发。当系统引入外加周期力信号时，如图2所示，系统平衡状态被打破，双稳态势阱函数在外加周期力的影响下会形成规律的倾侧现象，其频率与外加周期力相同。

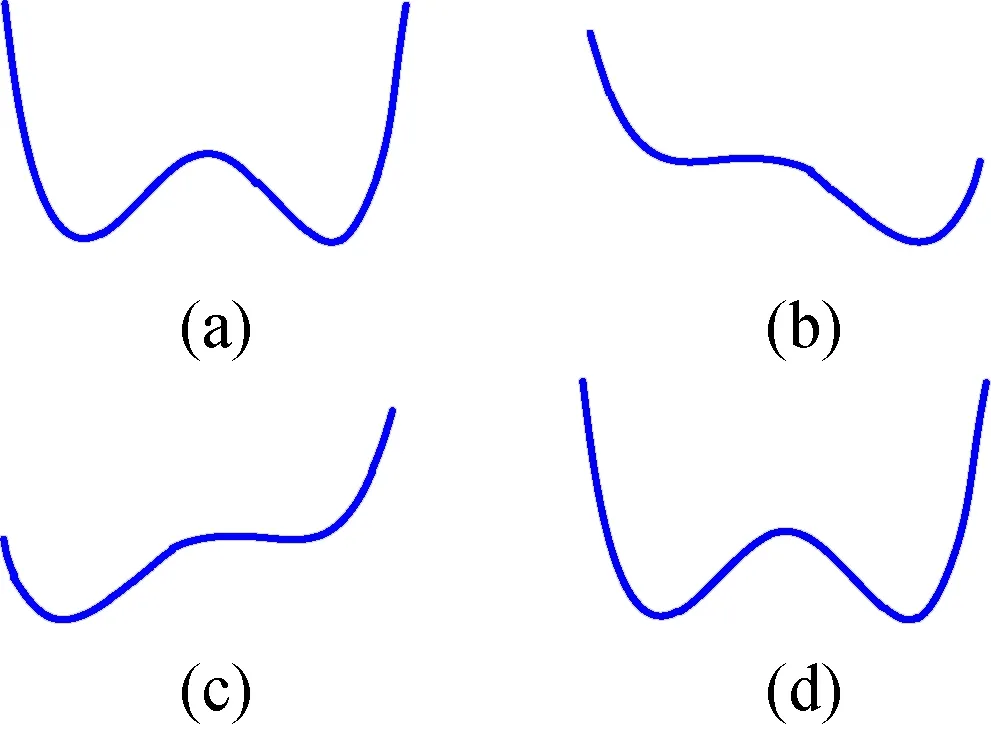
图2 势函数周期性侧倾示意图

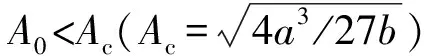
2.2 分数阶随机共振系统

本节将引入广义郎之万方程理论依据结合分数阶算子定义，在过阻尼的情况下，将其推广至分数阶。

分数阶微积分最常用的定义有以下3种：Riemann-Liouville(RL)，Grünwald-Letnikov(GL)和Caputo[15,16]。本文将首先简略介绍后两种定义。

G-L分数阶微分定义如式(3)所示：

α>0

(3)

Caputo定义如式(4)所示：

(4)

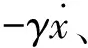
(5)

(6)

在粘性非均匀介质中，粒子在介质中的运动在过去时刻上具有记忆性，是经典的非马尔科夫过程[17]。因此可以将经典郎之万方程推广至广义郎之万方程，即阻尼核函数为时间相关函数γ(t)，此时广义郎之万方程如下所示：

(7)

式中：ζ(t)为随机噪声项，其与阻尼核函数γ(t)满足如下涨落耗散定理：

〈ζ(t)ζ(t′)〉=mkBTγ(t-t′)

(8)

而在一些实际现象中，介质对速度往往具有记忆性。其表现为离当前间隔越近，其关联程度越强，离当前间隔越远，其关联程度越差[18]。这种记忆性可以认为是幂律记忆性，此时上述阻尼核函数γ(t)可如式(9)所示：

(9)

由上式可知阻尼核函数γ(t)随着时间t的幂次衰减，α越大衰减速度越大。将式(9)代入式(7)中，则有：

F(t)+ζ(t)

(10)

而结合本节开头所介绍的分数阶微积分定义,可得：

(11)

此时在过阻尼情况下，可由推导出分数阶郎之万方程如式(12)所示：

(12)

3 分数阶随机共振系统的FPGA实现

3.1 分数阶双稳态系统设计

由于分数阶随机共振系统结构的复杂性，众学者对其研究主要停留在数学理论研究及仿真研究阶段，对于分数阶随机共振系统的硬件实现还处于起步阶段。本章将以上述分数阶Langevin方程为理论基础，提出一种分数阶双稳态随机共振系统的FPGA实现方法。

令式(12)中的结构势函数为ax-bx3，微弱有用信号为Acos(2 π ft)，则此时分数阶随机共振系统的数学模型为：

Dαx(t)=ax-bx3+Acos(2 π ft)+ζ(t)

(13)

对式(13)左右两边同时分数阶积分，可以得到：

x=I-α[ax-bx3+Acos(2 π ft)+ζ(t)]

(14)

式(14)可用一个带反馈的非线性系统表示，其结构框图如图3所示。

图3 分数阶随机共振系统结构框图

该系统由加法环节，分数阶积分环节、比例放大以及幂运算环节组成。其基本设计思想为，利用FPGA中的乘法器构建出式(12)中需要分数阶积分的几项，并通过加法器进行求和，最后输入分数阶积分器进行积分，最后将积分结果输出。

3.2 分数阶积分器设计

分数阶积分器和微分器的实现可分为基于连续时间或离散时间近似实现两种。在连续时间近似中，可通过采用高阶有理系统来逼近分数阶算法实现，如Oustaloup，Carlson方法迭代等。离散时间近似的分数阶微积分实现可分为直接法或间接法实现。间接法通过获得一个连续时间近似来拟合频域，然后通过幂级数展开、麦克劳林级数展开泰勒级数展开对其离散化处理来实现。本节将基于Grünwald-Letnikov分数阶定义，采用短记忆原理，实现分数阶积分器的FPGA实现。

无限阶滤波器在物理上是不可实现的，为了在FPGA上实现Grünwald-Letnikov定义算子，在此采用了长度为L的近似有限窗口变式，如式(15)所示：

(15)

式中：h是步长；L是窗口大小。

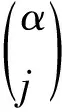
图4 输入与二项式系数的乘积

按照上述近似有限窗口变式即可将GL定义的分数阶微积分近似为有限次数的乘法和加法运算，为下述分数阶微积分的硬件实现提供了理论依据。

固定窗口法GL算子的硬件实现如图5所示。其中寄存器用于存储输入信号数据。输入与输出信号均采用32位定点数，整数部分是6位，小数部分是26位。与浮点数相比，采用定点数运算提高了系统的性能，降低硬件成本。第一个查找表LUT用于存储w0到wn-1的二项式系数，第二个查找表LUT中d0到dn-1用于存储x1w1+d1到xnwn-1+dn-1的相加结果。通过改变α的值即可生成对应的二项式系数，从而调整分数阶积分器的阶数。

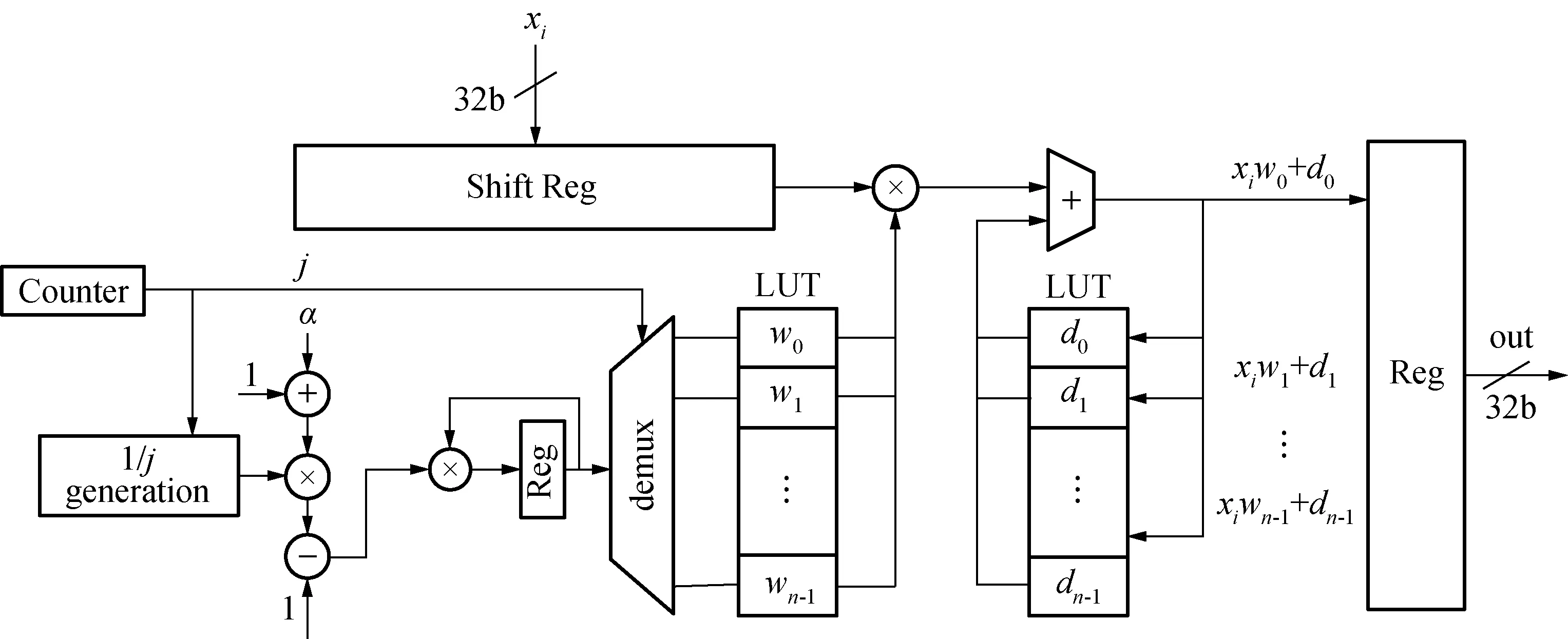
图5 固定窗口法实现GL算子的硬件架构

上述分数阶算子的FPGA实现其具体步骤如下：

(1)将所有输入信号都存储在移位寄存器中，并在每个周期进行移位；

(2)根据给定的分数阶阶数α和窗口大小L生成二项式系数w0到wn-1，并将其存储在第一个查找表中，第二个查找表d0到dn-1都置0；

(3)将移位寄存器中最后一个输入信号值与第一个查找表中所储存的二项式系数相乘；

(4)将乘法器输出结果分别与第二个查找表中的d0到dn-1相加；将xiw0+d0作为输出，不存储在第二个查找表中，将xiw1+d1到xiwn-1+dn-1的结果存储在第二个查找表d0到dn-2中，其中dn-1为零。

为验证上述算法的有效性，以文献[19]中的改进Oustaloup算法分数阶算子进行对比实验。设定分数阶阶数α=0.7，窗口大小L=30，输入信号为三角波信号。图6给出了固定窗口算法分数阶积分器FPGA实现结果及改进Oustaloup算法仿真结果。

通过数据对比，固定窗口法分数阶积分器的FPGA实现与改进Oustaloup算法仿真结果具有较好的一致性，验证了上述算法可准确的用于分数阶随机共振系统。

4 仿真实验及分析

本章将通过实验仿真验证上述分数阶系统能否产生随机共振现象，提高信号信噪比。在实际应用现场，一般情况下，待检测的周期信号往往十分微弱且带有一定的噪声，故要增大有用周期信号的幅值是很难实现的，而分数阶阶次可由上述系统调整。因此，仿真实验仅讨论分数阶随机共振特有的参数,即分数阶阶次对该系统的影响。

微弱周期信号与高斯白噪声可由外部信号发生器提供，这里设定噪声强度D=3,有用信号幅值A=0.3，频率为f=0.01 Hz。

图7是噪声与有用信号混合时的时域图及功率谱图。

图7 输入信号时域图及功率谱图

从图7结果显示，未经处理的周期信号完全被噪声所污染，并且在频谱中微弱周期信号的频率分量也非常小，很难提取出有用信号。接下来将该信号输入上述分数阶双稳态随机共振系统，设定系统的结构参数a=1，b=1，同时令分数阶阶数α以步长为0.05从0.05递增到1，并计算得到其频谱。图8分别为分数阶阶次为0.3和0.55时经系统处理后的时域图与频谱图。

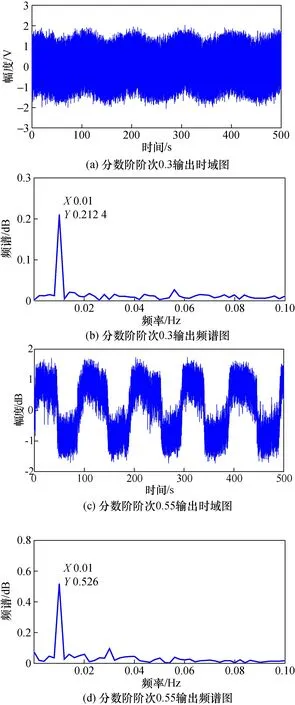
图8 分数阶阶次0.3、0.55时系统输出时域图与频谱图

从图8(a)和图8(b)可以看到，当分数阶阶次是0.3时，系统处于欠共振状态，此时频率为 0.01 Hz 对应的频谱值为0.212 4，微弱信号快要被噪声所淹没。当分数阶阶次增加到0.55时，粒子在两稳态间周期性跃迁，且其频率与微弱周期信号一致，系统进入随机共振状态，此时频率为0.01 Hz对应的频谱值为0.526 0，可以看到检测效果远远好于阶次为0.3时。

随后进一步分析可以得到分数阶阶次与频谱值的关系，如图9所示。图9中可以发现，随着分数阶阶次的增加，频谱值也随之增大至一个极大值点，此极大值点为最优分数阶阶次。继续增加阶次，系统势垒高度增加，粒子逐渐难以跨过势垒，抑制了随机共振现象的发生，此时其频谱值反而减小。

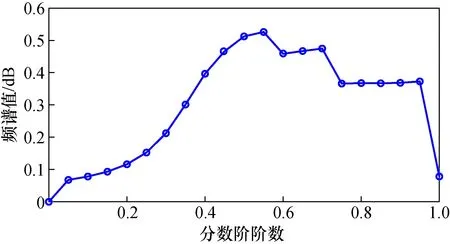
图9 频谱值与分数阶阶次关系图

从上述仿真实验结果表明，该分数阶双稳态系统可以有效提高微弱周期信号的信噪比，并且存在一个最优分数阶阶次，使得系统输出信噪比增益最大。

5 结 论

本文将传统随机共振理论推广至分数阶，提出一种现场可调整参数的分数阶双稳态随机共振系统的FPGA实现方法，并通过仿真实验验证该系统有效性。仿真实验结果如下：

(1)通过调节至合适的分数阶阶数，该系统可以产生随机共振现象。

(2)随着分数阶阶次增大，系统输出增益增大至极大值，继续增大分数阶阶次则随机共振现象被抑制，即存在一个最优分数阶阶次，使系统输出增益最大。

综上所述，该分数阶系统能有效从被噪声干扰的信号中提取出微弱有用信号，具有一定的应用价值。

但是，对于不同的信号，其产生随机共振现象的参数不同，现场人工试凑寻找最优参数较为困难，这限制了其应用前景。下一步，主要研究可集中于根据输入信号实现分数阶随机共振系统的自适应控制，为实际工程应用奠定基础。