基于转移概率地质统计的淮南顾桥矿区松散层含水介质刻画

邓 辉，马 雷，高 迪，赵卫东，杨 曼

(合肥工业大学 资源与环境工程学院，安徽 合肥 230009)

0 引 言

地下水作为地球上重要的水体，与人类社会有着密切的关系，是必不可少的重要水资源[1]。含水介质的空间分布存在着较强的非均质性，导致在对含水介质进行三维建模时往往难以得到准确的模拟结果，并存在较大的不确定性。因此，如何使用地质统计方法对含水介质进行准确刻画是一个重要问题。

近年来经过不断的发展，已经有多种用于随机模拟的建模方法，如序贯高斯模拟、序贯指示模拟、多点地质统计和转移概率地质统计等[2-6]。其中转移概率地质统计方法可以刻画重要的水文地质结构信息，在用于描述区域化变量的空间变化时被证明可以很好地反映复杂空间的变异性[7]。传统的地质统计方法是基于交叉变差函数得到地质统计模型，但传统的方法对于描述复杂空间的连续性往往存在局限性，如对地质体的不对称分布往往考虑欠佳，很难将关于地质类型分布比例、地层平均长度、转换趋势等信息有效地集成在交叉变差函数模型中。因此，基于马尔可夫链的随机模型被引入到地质统计领域中，拓展了传统的地质统计方法，特别是对含水介质非对称性的模拟有很大的提升[8]。转移概率地质统计模型可以很好地考虑水文地质结构的空间变异性，而且在建立模型的过程中，融入了地质类型分布的比例、平均长度和相互间的转换趋势等地质统计信息，使建模过程更直观，更易于理解[2]。

为了对含水介质进行准确模拟，表征含水介质空间分布的复杂性和随机性，吴诚云[9]基于马尔可夫链随机场理论，建立三维马尔可夫链地层结构预测模型，验证了三维马尔可夫链模型应用在三维地层结构模拟方面的科学性、正确性和适用性，同时分析了钻孔数量对于获得稳定模拟结果的影响。刘景兰等[10]基于马尔可夫链的多元地质统计模型建立了550 m深度范围内三维水文地质结构模型，对水文地质层进行划分，结果表明该方法可以较为真实地刻画出研究区的三维地质结构。孙倩等[11]根据钻孔资料使用转移概率地质统计方法建立了岩相空间分布的地质模型，并考虑岩性与水文地质参数之间的关系建立地下水流预测模型。在三维地质模型的基础上，许多学者进行了地下水流数值模拟及不确定分析相关方面的进一步研究[12-17]。为了证明转移概率地质统计方法的优势性，He等[18]使用转换的地球物理数据结合钻孔数据建立转移概率和马尔可夫链模型，通过调节“软”数据与“硬”数据的使用并借助转移概率地质统计软件有效地刻画了研究区的水文地质结构特征。Christensen等[19]基于马尔可夫链蒙特卡洛方法实现了大区域的水文地质结构模拟，并充分地结合航空电磁数据和钻孔数据，显著提高了大规模地质构造的模拟精度。蔡永敏[20]对耦合马尔可夫链模型进行改进，发现使用改进的耦合马尔可夫链模型能够较好地模拟地质剖面内不同倾斜方向的地层交界面及变异地层。由于可以更好地模拟地质结构的空间连续性，基于马尔可夫链的转移概率地质统计法作为一种含水介质建模的随机方法得到了广泛应用[21-25]。

本文首先对淮南顾桥矿区的钻孔数据进行概化处理，将矿区的钻孔岩性概化为4类含水介质，再使用概化后的钻孔数据利用转移概率地质统计方法进行含水介质的空间分布模拟，得到研究区的含水介质空间分布模型。最后将矿区原始的水文地质剖面与随机模型中相应位置的模拟剖面进行比较，并使用不同方向的剖面进行剖面之间的综合对比，据此验证转移概率地质统计方法在刻画矿区含水介质空间分布的可靠性。

1 研究区概况

淮南顾桥矿区地处淮河中游淮北平原南部，地形平坦，地面标高一般为21～24 m，总体地势为西高东低、南高北低(图1)，矿区总面积为106.737 km2。其地理坐标为东经116°32′06″—116°38′53″、北纬32°43′46″—32°51′50″，属于淮北平原暖温带半湿润季风气候区。区内气候温暖，雨水充足，年平均降水量为1 134.8 mm。顾桥矿含水层(组)由新生界松散砂层含水层(组)、煤系砂岩裂隙含水层(组)和石灰岩岩溶裂隙含水层(组)组成，各含水层对矿床开采的影响程度又可分为直接充水含水层(组)和间接充水含水层(组)，各含水层(组)之间一般都由有效隔水层(组)和相对隔水层(组)间隔。井田地下水的运动受控水构造和沉积条件的控制，形成了由浅层潜水过渡到深层承压水类型，以及明显的水质垂向分带。地下水运动的特点为：水平运动缓慢，垂直运动停滞，浅部补给水源充沛，深层补给水源贫乏，承压自流水排泄条件阻塞。

2 理论和方法

2.1 转移概率

在基于马尔可夫链的地质属性建模方法中，转移概率作为马尔可夫链的核心被用来描述区域化空间变量的变化，转移概率的定义为在x点处是地质类型j的条件下，点(x+hφ)处是地质类型k的概率，数学表达式如下：

tj,k(hφ)=Pr{k(x+hφ)|j(x)}

(1)

式中：j和k为两点的地质类型；hφ为两点间的位置距离，即空间步长；tj,k(hφ)是相距hφ两种岩性的转移概率。

与传统的地质统计模型相比，理论上基于马尔可夫链的地质统计建模方法可以获得任意步长hφ的转移概率。因此，在表征地质类型的空间连续性方面转移概率有着一定的优势性。

2.2 马尔可夫链的建立

地质统计模型所采用的马尔可夫链主要有连续型马尔可夫链、离散型马尔可夫链和嵌入型马尔可夫链。由于需要表征地质体的空间连续性，采用连续型马尔可夫链来表示地质空间连续属性，用空间步长hφ替代连续的时间间隔t，从而将马尔可夫链从时间域的描述转换为空间域内对地质类型的描述。数学上，连续马尔可夫链是一个通过矩阵指数函数描述的转移概率模型。基于空间的一维转移概率矩阵T(hφ)的函数表达式为：

T(hφ)=exp(Rφhφ)

(2)

式中：hφ表示在φ方向上一个步长距离，T(hφ)为K×K的转移概率矩阵，Rφ为K×K转移强度矩阵。其中，

Prepared a draft of the manuscript: Muppala S,Gajeton J

(3)

(4)

式(4)中：rjk,φ表示在φ方向上从类别j转换到类别k的转移强度。

转移强度矩阵表示的是转移概率随着距离变化而变化的强度，通过定义转移强度矩阵可以方便地定义马尔可夫链模型。对于具有N种地质类型的马尔可夫链模型需要定义一个N×N的转移强度矩阵。转移强度定义为：

(5)

由于在实际复杂的地质条件下需要建立三维空间的模型才能解决实际问题，转移概率值不仅会在不同距离上发生变化，也会在不同方向上发生变化。因此需要在一维空间的马尔可夫链模型的基础上，构建三维空间的马尔可夫链模型。对于各向异性的马尔可夫链建模，首先要确定主方向，主方向可以通过地质特征，如地质体的延伸方向、倾向、层理面等来确定，通过这些方向构造笛卡尔三维坐标系x、y、z。然后求出主方向上马尔可夫链的转移强度矩阵。最后建立将主方向转移强度转化成任意方向马尔可夫链转移强度的数学表达式：

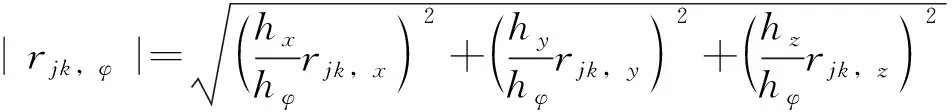
(6)

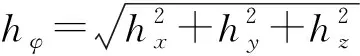
2.3 条件模拟

条件模拟包括两步：(1)使用序贯指示模拟建立一个初始模型；(2)使用模拟退火算法对产生的序贯指示模拟的初始模型进行迭代模拟以优化模型。条件序贯指示模拟使用转移概率指示协同克里金替代原来的基于指示协方差的克里金，其他与序贯指示模拟算法相同[26]。转移概率地质统计中使用模拟退火算法对分类变量条件模拟进行“后处理”，其目的是通过比较模型提高模拟结果与实测变量的空间变异性的吻合度[27]。

本文的含水介质随机模拟采用转移概率地质统计方法，利用马尔可夫链建立含水介质空间变异的统计模型，使用序贯指示模拟和模拟退火算法优化生成含水介质三维随机模型。综上所述，利用转移概率地质统计方法模拟含水介质分布有三个主要步骤。首先，在垂直和侧向(走向和倾向)方向上对转移概率矩阵中的项进行椭球插值，建立三维转移概率模型。根据钻孔岩性统计数据、连续性地层分布、先验知识等计算实测的岩性转移概率，再对实测的转移概率进行拟合，得到连续的空间马尔可夫链模型。然后，利用马尔可夫链模型代替指示变差函数进行序贯指示模拟，得到初步的三维水文地质结构模型。最后，利用模拟退火算法对建立的模型进行后处理优化，提高模拟和建模数据的空间变异性的一致性，得到最终的三维水文地质结构模型。

基于上述理论和方法，马雷[12]研发了一款基于GIS的集水文地质数据管理，数据(钻孔、点、线、面、栅格)尺度综合计算，转移概率地质统计随机模拟，含水介质的确定-随机耦合模拟和随机-随机耦合模拟等功能于一体的多尺度岩性模拟系统。本研究将在该系统下利用大量钻孔数据进行顾桥矿区松散层含水介质模拟。

3 结果与讨论

3.1 顾桥矿区含水介质模拟

由顾桥矿区的钻孔资料可知，区内岩性以黏土、砂、砾、泥岩、灰岩和砂岩为主，可以将所有的钻孔岩性按含水和透水性概化成4类，分别是含水介质、弱透水介质、弱隔水介质和隔水介质。在研究区内共收集358个钻孔数据进行含水介质模拟，钻孔密度为3.4个/km2。首先对淮南顾桥矿区钻孔4类介质进行厚度细化，取空间步长为1 m，分别建立4种介质相互的转移概率矩阵；然后在进行随机模拟过程中，对模型在x、y和z三个方向上进行网格剖分，网格数量参数设置为100×156×200，4种介质侧向与垂向长度比经调试分别设置为6.886、10.964、4.990和6.852，最终运行TSIM进行条件模拟。先使用序贯指示模拟建立一个初始模型，再使用模拟退火算法对产生的序贯指示模拟的初始模型进行迭代模拟以优化模型。

3.2 剖面对比分析

利用转移概率地质统计建立的松散层含水介质模型如图2所示，根据钻孔资料和勘探线的布置在模拟结果模型中通过点选与原始剖面对应的钻孔，在钻孔数据匹配一致的基础上选择了4条模拟剖面和与之对应的原始水文地质剖面进行对比分析，分别为三线、十三线、十五线和二十线。三线位于研究区的北部，线上共有14个钻孔用来进行剖面位置模拟结果的对比分析。由三线的模拟结果(图3(a))可以看出，这部分地层有两个明显的含水层和两个隔水层，其中中部的含水层相对较厚而底部的含水层相对较薄。在原始水文地质剖面图3(b)中也可以看到两个含水层和两个隔水层与之相对应，并且两者保持较一致的分布特征。

十三线和十五线分别位于研究区的中部和南部，两条模拟剖面中各有12个钻孔用来进行剖面位置模拟结果的对比分析,模拟结果分别如图4和图5所示。十三线和十五线总体上可以分为上下两个隔水层和中间较厚的含水层。由图4(a)和(b)与图5(a)和(b)的比较可以看出，含水层与隔水层都能被准确地模拟刻画出来，并保持较一致的空间分布。在图3(a)、图4(a)和图5(a)的含水层中都包含着若干个较薄的隔水性质的透镜体(层)，这同样与原始水文地质剖面(图3(b)、图4(b)和图5(b))一致，表明转移概率地质统计方法在刻画介质非均质性方面具有良好的效果。这三组剖面的对比分析显示，转移概率地质统计方法可以较好地模拟出顾桥矿区的含水介质空间分布，既体现了矿区松散层含水介质的空间变异性，又准确地表征了介质的横向连续性分布。

考虑到含水介质具有各向异性，本研究选择了一条近南北方向的原始水文地质剖面(二十线)与模拟剖面进行对比分析(图6)。在二十线中共包括17个钻孔，模拟剖面(图6(a))和原始水文地质剖面(图6(b))中的含水介质有着较一致的空间分布特征，包括上部薄隔水层、中部厚含水层、下部厚隔水层以及剖面右下角的局部含水层。其中，中部厚含水层中包含着薄隔水性质的透镜体(层)，并且与三线、十三线和十五线模拟剖面中的含水介质划分相对应，说明转移概率地质统计方法对地质体的各向异性也具有较好的处理效果。

根据模拟结果可以将顾桥矿区松散层模拟剖面划分为中上部强非均质区和深部弱非均质区。在图3—图6的模拟结果对比中可以发现，在弱非均质区含水介质空间变异性小，介质的空间连续性大，在模拟剖面中表现为含水层或隔水层分布连续且完整。通过与原始水文地质剖面的对比，发现转移概率地质统计方法对于弱非均质的空间连续性模拟效果较好。而对于强非均质区，含水介质空间变异性较大，介质的空间连续性相对较弱，在模拟剖面中表现为含水层与隔水层在垂向和侧向的不连续发育。一般来说，转移概率地质统计方法作为一种随机模拟方法，对于强非均质区的模拟，在钻孔数据有限的情况下其模拟效果欠佳。但在顾桥矿区的含水介质模拟中，强非均质区的模拟结果与其在原始水文地质剖面中分布情况基本保持一致。这说明钻孔密度基本可以满足顾桥矿区含水介质在该尺度下准确模拟刻画的需求。

4 结 论

基于转移概率的地质统计方法相较于传统的地质统计方法做出了改进，使用转移概率替代了传统的交叉变差函数来描述区域化空间变量的变化，简化了地质空间各向异性的处理过程。同时，该方法较为完善地模拟地质空间的不对称分布和各向异性。本文对顾桥矿区的含水介质建立了三维模型，使用矿区原始水文地质剖面与模拟剖面进行对比，得到如下认识：

(1) 模拟结果较好地表征了矿区4种地质类型的分布情况。原始水文地质剖面和模拟剖面的对比分析表明，含水层与隔水层分布基本保持一致，较准确地刻画了矿区含水介质的空间分布特征。

(2) 在钻孔密度为3.4个/km2的情况下，转移概率地质统计方法不仅对研究区的弱非均质性有较完善的刻画，对研究区的强非均质性也有较好的模拟效果。这体现了转移概率地质统计方法在刻画三维含水介质空间分布及其非均质性中的有效性与优势性。

(3) 南北方向剖面和东西方向剖面之间有很好的对应关系，三线、十三线和十五线模拟剖面中的含水介质分布与二十线模拟剖面中的含水介质有着一致的分布特征，说明转移概率地质统计方法对于地质体的各向异性也能较准确地刻画。