Number-of-constituent-quark scaling of elliptic flow:a quantitative study

Meng Wang · Jun-Qi Tao · Hua Zheng · Wen-Chao Zhang · Li-Lin Zhu ·Aldo Bonasera

Abstract The number-of-constituent-quark(NCQ)scaling behavior of the elliptic flow of identified particles produced in A+A collisions is studied quantitatively using an empirical function that fits the experimental v2 data available from the RHIC and LHC.The most common approach for NCQ scaling involves (1) doing a scaling of the experimental v2 data of an identified particle with its NCQ,(2) doing the same to its transverse momentum or energy,then (3) combining all the scaled data and identifying the NCQ behavior by intuitively looking (since the measured experimental data are discrete). We define two variables（d1，d2） to describe NCQ scaling quantitatively and simultaneously,and identify the approximate region where the NCQ scaling holds. This approach could be applied to study NCQ or other scaling phenomena in future experiments.

Keywords Number-of-constituent-quark scaling · Heavyion collisions · Elliptic flow

1 Introduction

The main goal of producing relativistic nucleus-nucleus collisions at the RHIC and LHC is to create a deconfined quark and gluon plasma (QGP), a new state of matter that forms at a high density and temperature, as predicted by quantum chromodynamics (QCD), and to understand its properties [1-4]. The azimuthal anisotropies of the particles produced in the collisions have proven to be a powerful probe for investigating QGP characteristics and hadron structure [5-16]. Therefore, they have been extensively measured experimentally and studied both experimentally and theoretically. These anisotropies can be quantified in terms of the coefficients vnin the Fourierseries expansion of the particle distributions with respect to the reaction plane (RP), defined by the beam axis and the impact parameter, which is determined on an event-byevent basis [17-21]:

In practice, several methods have been proposed for analyzing the azimuthal anisotropies of the final particles.These include the event-plane method, the η-subevent method, the cumulant method, and the Lee-Yang-Zero(LYZ) method [5, 22-24]. Their purpose is to mitigate the non-flow contributions and the flow fluctuations.In the past two decades,the direct flow(v1)and elliptic flow(v2)have been measured experimentally at both the RHIC and LHC.One remarkable finding of the flow investigations conducted at the RHIC (and confirmed at the LHC) is the scaling of v2with the number of constituent quarks in a hadron, in cases where many particle species produced in high-energy nucleus-nucleus collisions in the low-transverse-momentum region [5-9, 20, 25]. Furthermore, at both the RHIC and LHC, this scaling is seen to improve when expressed as a function of the scaled hadron transverse energy [5-8, 25]. This may be a consequence of energy conservation,as discussed in Ref.[10]based on the Boltzmann equation. This observation is consistent with the standard model, which considers quarks as the basic building blocks of all matter, and with quark coalescence as the hadronization mechanism [9-14, 17, 21, 26-35].This provides indirect evidence that a QGP is formed in high-energy nucleus-nucleus collisions.

Usually in experimental investigations of number-ofconstituent-quark (NCQ) scaling phenomena, both the experimental v2data and the transverse momentum or energy of an identified particle species are scaled with its number of constituent quarks.Then,the scaled v2is plotted as a function of the scaled transverse momentum or energy.NCQ scaling is then identified by eye because the experimental data measured are discrete. Several attempts have been made to quantitatively elucidate the NCQ scaling[5, 7, 23, 36]. Such studies adopt a polynomial function to fit the scaled v2as a function of the scaled transverse momentum or energy for a chosen particle species. (The chosen order of the polynomial,up to the seventh,depends on the particle of interest, the collision energy, and the fitting range of the scaled transverse momentum or energy.)This polynomial defines a baseline from which to calculate the deviation of the scaled v2for the other particle species.However, such a polynomial function is suboptimal because it may oscillate, and its behavior beyond the data range is determined by the sign of the coefficient of the largest-order term.Other forms of empirical functions have also been proposed to investigate the NCQ scaling by fitting the v2data for mesons and baryons simultaneously[17, 25, 37]. These are discussed in the next section. Considering the fact that the pT bins differ for mesons and baryons in experimental measurements, we here propose,as a plausible quantitative approach, to search for an empirical function capable of fitting all the experimental v2data and to conduct the investigation based on this analytical function.

The remainder of this paper is organized as follows.Section 2 briefly introduces two variables （d1，d2） to quantify the NCQ scaling of the identified particles simultaneously. The empirical functions quoted in the literature and our proposed empirical function for fitting the experimental v2data are also introduced. Section 3 shows the fit results of v2for different particle species from the beam energy scan(BES)program at the RHIC to LHC.The NCQ scaling is shown quantitatively to be a function of both the scaled transverse momentum and the scaled transverse energy. Section 4 closes with concluding remarks.

2 Method and empirical functions

Assuming that we know the information at any point of the scaled v2and the corresponding scaled transverse momentum or energy for each particle species, we can define two variables that simultaneously and quantitatively characterize the quality of the NCQ scaling.

The first variable is the deviation between the scaled v2for one particle species and the average of all the scaled v2values for the particle species of interest in the NCQ scaling at each scaled transverse momentum or energy. It can thus be defined as

with free parameters a, b, c, d, e,and f.We emphasize that the experimental v2data are well fitted by Eq. (7), as discussed in the next section.

3 Results

Fig.1 Dependence of v2 on pT for a protons in Au+Au collisions at=200 GeV with a centrality of 30-80%, and b for pions in Pb+Pb collisions at =2.76 TeV with a centrality of 30-40%.The data are obtained from Refs. [7, 8]. The methods used to extract v2 are labeled. The curves are the fit results for the v2 data using Eq. (7). The data/fit are shown in the bottom panels, respectively

Fig.2 (Color online)Dependence of v2 on pT for protons or charged particles produced in Au+Au collisions at the RHIC,and for pions or charged particles produced in Pb+Pb or Xe+Xe collisions at the LHC. The data are obtained from Refs. [7, 19, 20, 24, 25, 41]. The labels indicate the methods used to extract v2. The curves are the fit results to the v2 data using Eqs. [(5)-(7)] and the 6th-order polynomial, as indicated in the legend

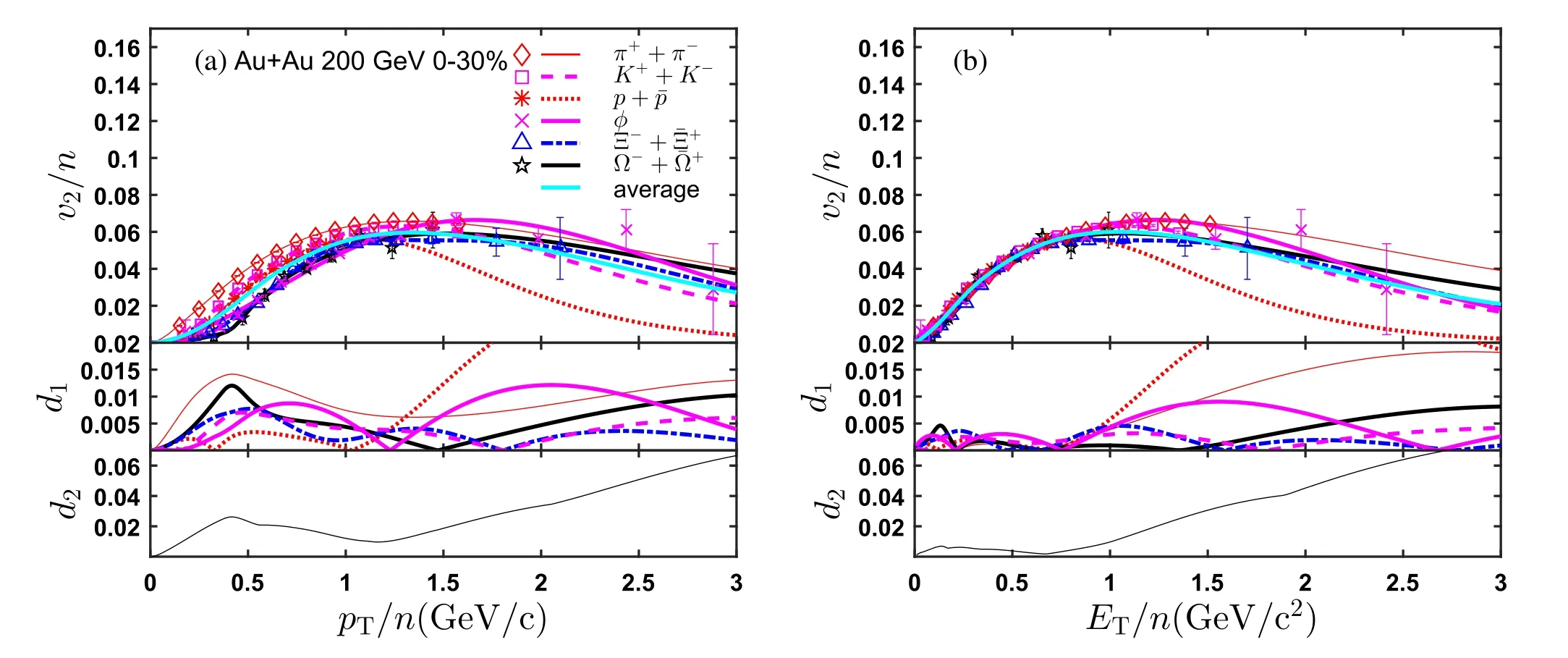
Fig. 3 (Color online) Scaled elliptic flow versus scaled transverse momentum (left panel) and energy (right panel) for the six identified particles (indicated in the legend) produced in Au+Au collisions at=200 GeV with centrality 0-30%. The curves for the fit results obtained using Eq.(7)and their averages are plotted.The two variables(d1，d2)are also plotted as functions of the scaled transverse momentum and energy, with appropriate scales for showing the details where NCQ scaling holds.The data are obtained from Ref.[7]

The fit results from the functions frequently adopted in the experimental papers, i.e., the polynomial function,Eqs. (5) and (6), are also shown. For the polynomial function,we choose a 6th-order polynomial as an example.The fitted curve at high pT clearly either increases or decreases depending on whether the sign of the coefficient of the highest order term is, respectively, positive or negative. Extrapolating the results based on this polynomial function is surely unreliable. Oscillations also appear when the fitting range is large. The empirical function in Eq.(5)can only fit the v2data for low and intermediate pT values, where v2reaches its maximum because Eq. (5) is constant at large pT by definition. Equation (5) is not guaranteed to equal zero at pT =0 GeV/c. Equation (6) is an improvement of Eq. (5) and can fit almost all of the v2data presented. We therefore adopted the empirical function in Eq. (7). There is a noticeable limitation for the extrapolation from the fit, which depends on how well the fitting function is constrained beyond the data points. This issue,common to all fitting functions,has consequences for our analysis, as discussed below. Therefore, the two variables d1and d2, defined in Sect. 2, are utilized to mitigate the problem caused by extrapolation beyond the data points. Fortunately, there is no need to extrapolate in the NCQ scaling region, and our conclusion is not affected.

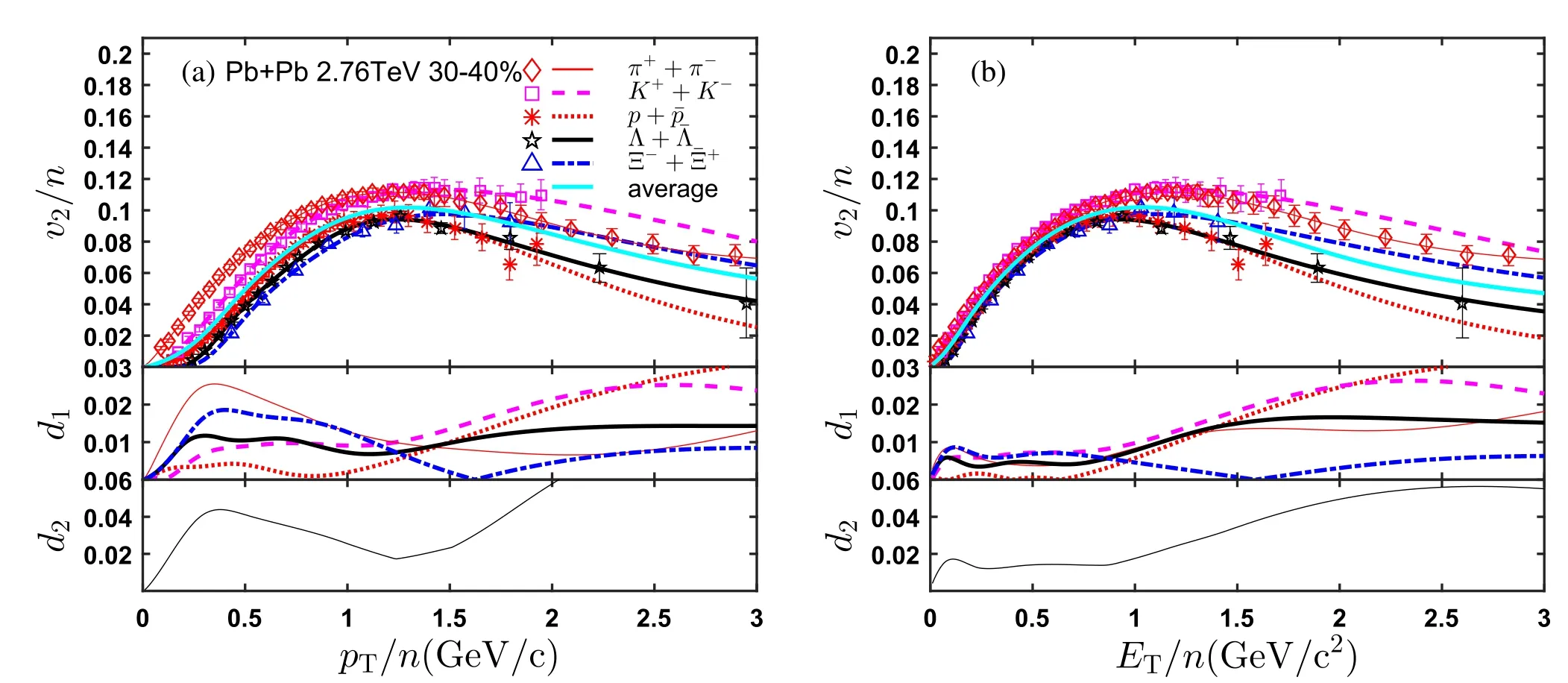
Fig.4 (Color online)Similar results to Fig.3 but for Pb+Pb collisions at =2.76 TeV with 30-40%centrality.The data are obtained from Ref. [8]

We can now quantitatively investigate the NCQ scaling of elliptic flow as a function of the scaled transverse momentum(or energy)of the identified particles produced in A+A collisions at the RHIC and LHC. Figures 3 and 4 show, respectively, the NCQ scaling of the elliptic flow v2of six identified particles, i.e., π++π-, K++K-, p+ ¯p,φ, Ξ-+ ¯Ξ+and Ω-+ ¯Ω+from Au+Au collisions at 200 GeV with centrality 0-30% at the RHIC; and the elliptic flow v2of five identified particles,i.e.,π++π-,K++K-,p+ ¯p, Λ+ ¯Λ and Ξ-+ ¯Ξ+from Pb+Pb collisions at 2.76 TeV with centrality 30-40% at the LHC. The values of v2for an identified particle are known to depend on the extraction method [5, 22-24]. This could affect the NCQ scaling when the v2data for different particle species of interest were extracted using different approaches in experiments. Therefore, we select the v2of the different identified particles extracted by the same method for one chosen collision system. The fit to the experimental data,obtained using Eq. (7) and the two variables （d1，d2）defined above, versus the scaled transverse momentum (or energy), are also shown.

4 Conclusion

To summarize, we have proposed an empirical function for fitting the elliptic flow v2data of the identified particles produced in A+A collisions at the RHIC and LHC. We also quantitatively investigate the NCQ scaling of the elliptic flow of the identified particles. This is done by utilizing the analytical empirical function to overcome the challenge posed by the discreteness of the experimental data. Thus, the NCQ scaling cannot be quantitatively investigated simultaneously for the scaled transverse momentum and energy. Given the issues associated with the extrapolation from the fitting function beyond the measured data region,particularly for Au+Au at the RHIC,two variables （d1，d2） are defined to quantify the NCQ scaling simultaneously. As expected, they not only give consistent results with those obtained by intuitively looking at the data (namely, that the NCQ scaling is better for the scaled transverse energy than the scaled transverse momentum); they also provide fine details of the region where the NCQ holds. This approach can be applied to study other experimental scaling phenomena quantitatively.

Author Contributions All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Meng Wang,Jun-Qi Tao and Hua Zheng.The first draft of the manuscript was written by Hua Zheng and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

10. L. Ravagli, R. Rapp, Quark coalescence based on a transport equation. Phys. Lett. B 655, 126-131 (2007). https://doi.org/10.1016/j.physletb.2007.07.043

11. V.Greco,C.M.Ko,Effect of resonance decays on hadron elliptic flows. Phys. Rev. C 70, 024901 (2004). https://doi.org/10.1103/PhysRevC.70.024901

12. R.J.Fries,V.Greco,P.Sorensen,Coalescence models for hadron formation from quark gluon plasma. Ann. Rev. Nucl. Part. Sci.58, 177-205 (2008). https://doi.org/10.1146/annurev.nucl.58.110707.171134

13. V.Greco,C.M.Ko,P.Levai,Parton coalescence at RHIC.Phys.Rev. C 68,034904 (2003). https://doi.org/10.1103/PhysRevC.68.034904

14. R.J. Fries, B. Muller, C. Nonaka et al., Hadron production in heavy-ion collisions: fragmentation and recombination from a dense parton phase. Phys. Rev. C 68, 044902 (2003). https://doi.org/10.1103/PhysRevC.68.044902

15. Z.W. Lin, L. Zheng, Further developments of a multi-phase transport model for relativistic nuclear collisions. Nucl. Sci.Tech.32,113(2021).https://doi.org/10.1007/s41365-021-00944-5

16. Z.B. Tang, W.M. Zha, Y.F. Zhang, An experimental review of open heavy flavor and quarkonium production at RHIC. Nucl.Sci. Tech. 31, 81 (2020). https://doi.org/10.1007/s41365-020-00785-8

17. X. Dong, S. Esumi, P. Sorensen et al., Resonance decay effects on anisotropy parameters. Phys. Lett. B. 597, 328-332 (2004).https://doi.org/10.1016/j.physletb.2004.06.110

29. K.P. Das and R.C. Hwa, Quark-antiquark recombination in the fragmentation region. Phys. Lett. B 68, 459 (1977). https://doi.org/10.1016/0370-2693(77)90469-5 [erratum: Phys. Lett. B 73,504 (1978)]. https://doi.org/10.1016/0370-2693(78)90776-1

30. R.C. Hwa, C.B. Yang, Inclusive distributions for hadronic collisions in the valon recombination model.Phys.Rev.C 66,025205(2002). https://doi.org/10.1103/PhysRevC.66.025205

31. R.C. Hwa, C.B. Yang, Scaling behavior at high pTand the p/π ratio. Phys. Rev. C 67, 034902 (2003). https://doi.org/10.1103/PhysRevC.67.034902

32. R.C. Hwa, C.B. Yang, Production of strange particles at intermediate pTin central Au+Au collisions at high energies. Phys.Rev. C 75,054904(2007). https://doi.org/10.1103/PhysRevC.75.054904

33. R.C. Hwa, L. Zhu, Spectra of identified hadrons in Pb-Pb collisions at LHC.Phys.Rev.C 84,064914(2011).https://doi.org/10.1103/PhysRevC.84.064914

34. L. Zhu, R.C. Hwa, Centrality and transverse momentum dependencies of minijets and hadrons in Au-Au collisions. Phys. Rev.C 88, 044919 (2013). https://doi.org/10.1103/PhysRevC.88.044919

35. J. Chen, D. Keane, Y.G. Ma et al., Antinuclei in heavy-ion collisions. Phys. Rept. 760, 1-39 (2018). https://doi.org/10.1016/j.physrep.2018.07.002

39. A. Andronic, V. Barret, Z. Basrak et al., Excitation function of elliptic flow in Au + Au collisions and the nuclear matter equation of state. Phys. Lett. B 612, 173-180 (2005). https://doi.org/10.1016/j.physletb.2005.02.060

40. W. Reisdorf, Y. Leifels, A. Andronic et al., Systematics of azimuthal asymmetries in heavy ion collisions in the 1A GeV regime. Nucl. Phys. A 876, 1-60 (2012).https://doi.org/10.1016/j.nuclphysa.2011.12.006