结构α-熵的加权高斯混合模型的子空间聚类
李凯,张可心
1 引言
近年来,随着信息技术、计算机网络与人工智能技术的不断发展,在实际问题中产生了大量高维数据,如何对这些数据进行聚类却遇到了很大的挑战. 尽管人们提出了一些不同的聚类算法,但由于高维数据的特殊性,使得传统聚类算法并不能直接应用于这些数据,为此,人们对高维数据的聚类进行了研究,其中方法之一是维数约简技术,该方法主要由降维和聚类两个独立的过程构成,且每个过程对聚类结果将会产生一定的影响,也就是说,利用该方法获得的嵌入特征对于聚类来说并不一定是最优的,且使得具有区分能力的信息丢失. 关于此问题,一些学者曾指出,若使用前几个主成分对数据聚类,则将破坏原数据的聚类结构[1]. 之后,人们提出了变量选择方法,较好地解决了降维和聚类过程独立的问题. 最近,Zhao等人[2]提出了基于正则项的高斯混合模型子空间聚类,此方法将聚类和寻找簇的子空间同时进行处理,进一步提高了子空间聚类的性能. Peng 等人[3]为了获取不同形状与大小的子空间,将权向量的负信息熵引入到扩展的高斯混合模型中,提出了一种基于熵的高斯混合模型的子空间聚类方法,然而该方法只考虑了信息熵. 我们知道,信息熵是结构α-熵[4]的特例,特别是,对于结构α-熵中参数α的不同取值,则其对应于不同的熵,例如,当α趋近于1时,结构α-熵变为信息熵;当α=2 时,则结构α-熵为平方熵. 另外,当α=2 时,基于结构α-熵的最小化准则等于最近邻方法的错误概率. 以上表明,将基于权向量的信息熵作为惩罚项并不总是获得较好的聚类结果. 针对结构α-熵,Li 等人[5]提出了最小熵的聚类方法,并将其应用于基因表达分析中,Nicholas 等人[6]提出了基于结构α-熵度量的点集配准,并且通过结构α-熵中参数控制求解的类型.
为此,本文通过扩展信息熵,研究了结构α-熵的加权高斯混合模型的子空间聚类.
2 相关工作
子空间聚类是指将数据划分为不同的子空间或簇,并且寻求数据的多个簇结构. 通常,子空间聚类可以分为四种类型,下面对其进行简介. 基于统计的方法将数据视为独立抽取且服从高斯混合模型的样本,子空间聚类问题被转化为模型参数估计,可使用EM(Expectation Maximization)算法或最大似然方法估计相应的参数[3,7]. 由于高斯混合模型具有较强的概率解释以及对噪声鲁棒性等优点,因此,该方法获得了较广泛的应用[8],然而,对于传统的高斯混合模型,当面对高维数据的聚类时,由于需要估计大量参数,以及维数的逐渐增大,则极大似然估计问题很快成为不适用的方法. 为此,人们通过修改目标函数或对协方差矩阵加以约束,提出了基于惩罚项的高斯混合模型的子空间聚类[2]. 基于代数的方法包括两种形式,一种是矩阵分解方法[9,10],通过对数据矩阵分解达到数据分割的目的,其缺陷是对数据噪声和异常数据较为敏感;另一种是广义主成分分析法[11],它主要使用多项式拟合数据,但由于数据中存在噪声,因此,该方法的实现较为困难,且对高维数据的处理代价较高. 基于迭代的方法将样本分配给子空间,并利用迭代技术更新子空间的簇,从而实现对数据的划分[13,14]. 此类方法可划分为硬子空间聚类和软子空间聚类. 硬子空间聚类通过使用启发式准则,采取自顶向下或自底向上的搜索策略,从所有特征中寻找簇所在的子空间.软子空间聚类通过分配特征权值确定簇所在的子空间,包括模糊加权子空间聚类[15~17]和熵加权子空间聚类[3,18,19]. 基于谱聚类的方法是将谱聚类算法作为框架,通过学习一个亲和矩阵找到数据的低维嵌入,并使用传统的聚类算法对低维数据聚类的一种方法. 亲和矩阵可以使用高斯核、局部信息或全局信息进行构造[20,21]. 最近,一些学者提出了对角为分块矩阵表示的子空间聚类以及复杂噪声下的子空间聚类,统一了现有的一些子空间聚类方法[22,23].
3 结构α-熵的加权高斯混合子空间聚类模型
假设样本集为X={x1,x2,…,xn},其中xk∊Rp(k=1,2,…,n),且xk是由c个高斯分量组成的混合密度中抽取的样本,概率密度函数如式(1)所示.
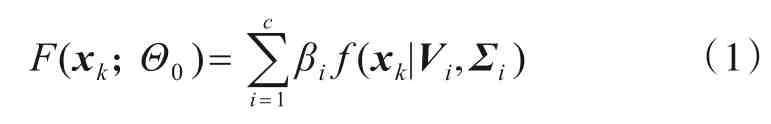
其中βi、Vi和∑i分别为第i个分量的混合系数、均值向量和协方差矩阵;f(xk|Vi,Σi)为第i个分量的高斯密度函数. 为了解决高维数据的子空间聚类,Peng等人[3]对高斯分量的协方差矩阵特例化,如式(2)所示.
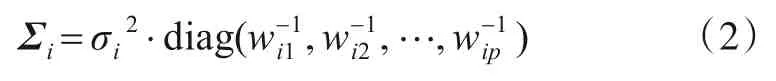
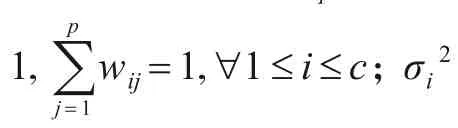
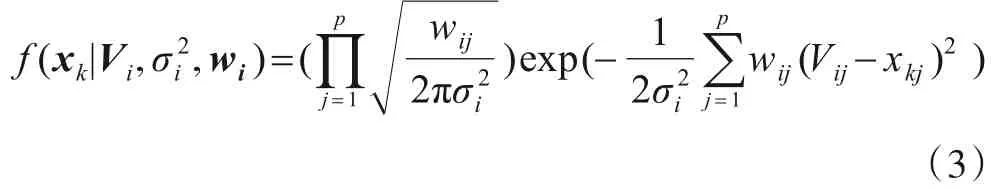
为方便起见,令Θ={(βi,Vi,σi2,wi)|1 ≤i≤c}. 为了估计Θ中的 参数,通过 最小 化KL 散度[3],从而 获得式(4):
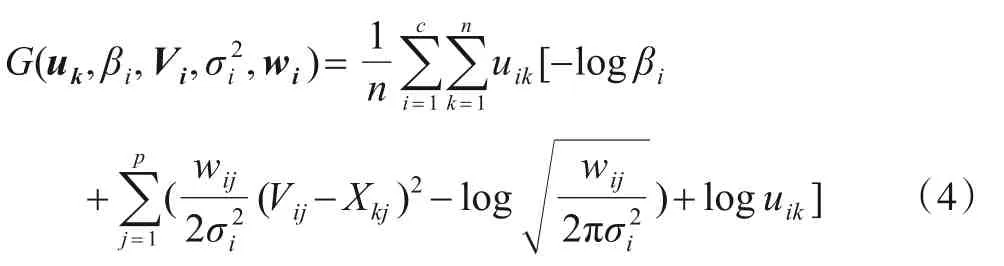
其中uk=(u1k,u2k,…,uck)是模糊隶属值组成的向量. 为了便于表达,下面给出了簇结构α-熵与聚类结构α-熵的定义.
定义1 设簇i的权向量为wi=(wi1,wi2,…,wip),则簇结构α-熵由式(5)计算.
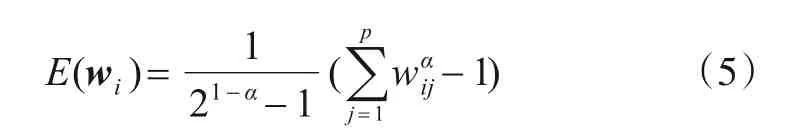
其中α≥0,α≠1.
定义2 聚类结构α-熵定义为所有簇结构α-熵的加权和,并由式(6)计算.
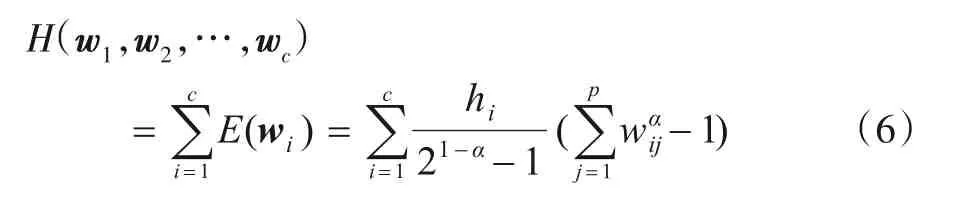
其中hi为加权系数.
可以看到,当α→1 时,则簇结构α-熵即为模糊熵,聚类结构α-熵为聚类模糊熵.
将聚类结构α-熵引入式(4),并结合约束条件,从而获得了结构α-熵的加权高斯混合子空间聚类模型,如式(7)所示.
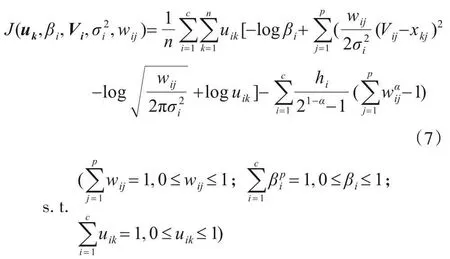
由式(7)可知,通过引入结构α-熵,并利用最小化KL 散度以及最大化聚类结构α-熵,使得算法能够获取质量较高的簇,权向量的聚类结构α-熵值越大,则越表明有更多的维度用于发现聚类中的簇,从而得到更好的子空间聚类结构.
4 结构α-熵的加权高斯混合模型子空间聚类算法
针对式(7),构造拉格朗日函数,如式(8)所示.
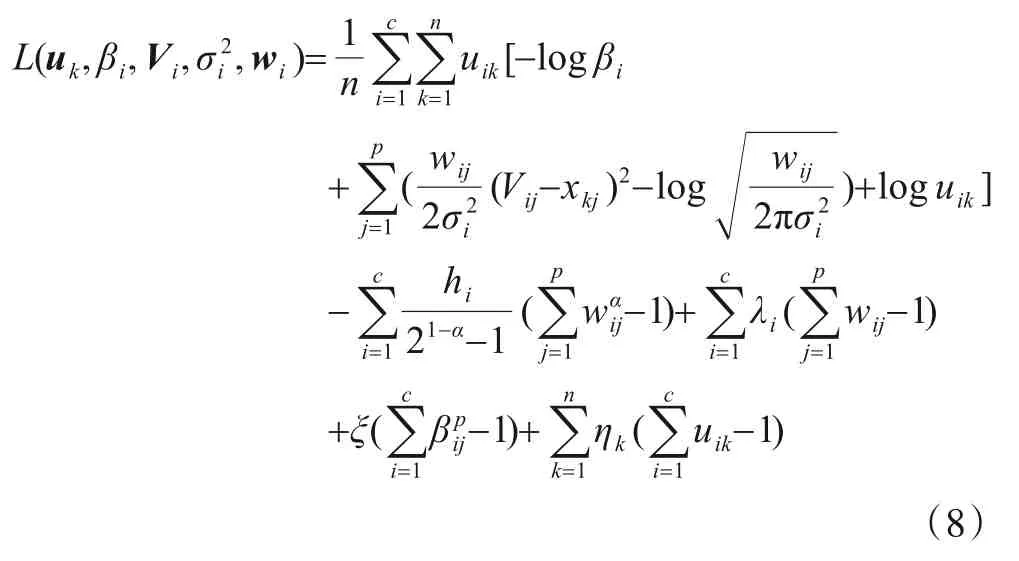
其中ξ为拉格朗日乘子,λ和η分别是由拉格朗日乘子λ1,λ2,…,λc和η1,η2,…,ηn构成的向量.
将式(8)分别对Vij、σi和βi求偏导,并令其等于0,从而得到式(9)~(11).
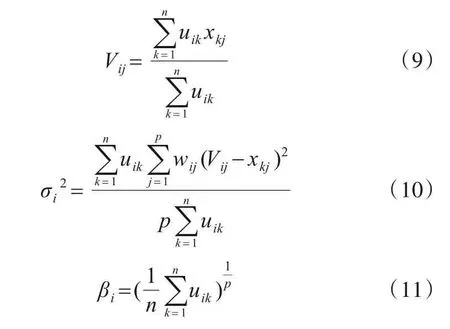
对于隶属度uik和特征权值wij的求解,下面以定理形式给出.
定理1 给定混合系数βi与权值向量wi=(wi1,wi2,…,wip),则式(8)取极值时满足的必要条件如式(12)所示.

定理2 给定混合系数βi以及隶属度uik,则式(8)取极值时满足的必要条件如式(13)所示.
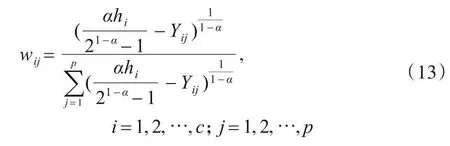
下面给出结构α-熵的加权高斯混合模型的子空间聚类算法SEWMM,如算法1.

可以看到,算法SEWMM 包括两种类型的参数,一种是具有约束的参数,例如wij、βi和uik,另一种是不具有约束的参数,例如σi和Vi.为了表明算法的收敛性,对于有约束参数,将式(8)关于wij、βi和uik求二阶偏导数,分别得到式(14)~(16).
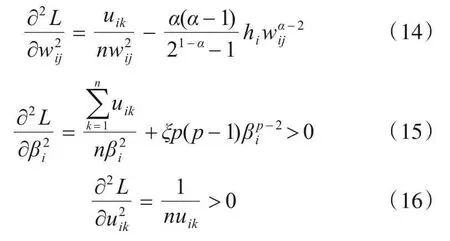
由α>0 与α≠1 知,式(14)大于零,且式(15)与(16)也大于零.
对于无约束参数σi和Vi,它们为极小值的证明可参考EM算法收敛性证明方法.
由以上结果可知,对于第t次迭代,则有
J(uk(t),βi(t),Vi(t),σ2i(t),wij(t))≤
J(uk(t-1),βi(t-1),Vi(t-1),σ2i(t-1),wij(t-1))
此式表明函数J(uk(t),βi(t),Vi(t),σ2i(t),wij(t))关于变量t是一个非增函数,从而可知算法是收敛的. 假设算法迭代T次收敛,由算法可知,其时间复杂性为O(npTc).
5 实验研究
为了验证算法SEWMM 的有效性,实验选取了UCI标准数据集与图像数据集,聚类评价指标分别为正确率(Accuracy,Acc)、兰德指数(Rand Index,RI)和标准互信息(Normalized Mutual Information,NMI),它们的取值范围均为[0,1];参数α的取值范围为[0.2,25],δ=10,实验结果为十次聚类的平均值.
5.1 UCI数据集
在UCI 标准数据集[24]中,选取了Sonar、WBCD、SPECT Heart、Vehicle、Semeion、Water Treatment Plant(WTP)、Ionosphere、Iris、Mfeat_zer(MFeat 的子数据集)和Liver 数据集进行了实验,并与ESSC[25]、FWKM[15]、EWKM[18]、CKS-EWFC-F[26]、PFSCM[14]、kSDC[13]、MoG[23]、RGMM[22]和EWMM[3]算法进行了聚类性能比较,实验结果如表1 所示,其中每个数据集所对应的三行数值分别为Acc、RI 和NMI 指标. 可以看出,算法SEWMM 在大部分数据集上获得了较好的聚类结果.例如,对于数据集Ionosphere、Semeion、Iris、WBCD、Ve‑hicle 与Liver ,在选取的三个指标上,提出的算法均获得了较高值,而在Vehicle 和WBCD 数据集的Acc 指标略低于MoG 和EWKM 算法,但其值基本相当. 对于剩余的四个数据集,在选取的Acc、RI 和NMI 中的两个指标都超过了比较的算法,而对于另一指标,提出的算法与获得较好结果算法的性能也基本相当. 同时,提出的算法在十个数据集的聚类性能优于EWMM. 以上表明,通过引入结构α-熵惩罚项,提出的算法在Acc、NMI 与RI上优于比较的算法.
5.2 图像数据集
本小节主要选取图像数据集进行实验和比较,包括BSDS500 图像与较大规模图像数据集,实验中使用的图像均为彩色图像转换后的灰度图像.
5.2.1 BSDS500图像
针对BSDS500 图像数据集[27],选取其中的16 幅图像对提出的算法SEWMM 进行了图像分割实验,比较算法分别为NCuts[28](记为NCuts1)、多尺度NCuts[29](记为NCuts2)、FLICM[30]、DSFCM-N[31]、FSC[16]、kSDC[13]、CKS-EWFC-F[26]、PFSCM[14]和EWMM[3]. 为了衡量算法的总体性能,在实验中,将不同算法分别在16幅图像获得的Acc、RI 和NMI 指标值进行了平均,实验结果如图1 所示. 可以看到,对于选取的所有图像,在聚类指标Acc 和RI 上,算法SEWMM 均优于比较的算法,而在NMI指标上,算法SEWMM 略低于NCust2;另外,我们也看到,在所有三个聚类指标上,提出的算法SEWMM 的指标值都高于算法EWMM.
5.2.2 图像数据集的聚类
本小节选取CIFAR10[32]、CIFAR100[32]、MNIST[33]、Fashion-MNIST[34]和USPS[35]图像测试集对提出的算法进行了实验;同时,选取NMF[36]、SSC[20]、SSC-OMP[37]、LRR[21]、LSR[38]、LRSC[39]、EnSC[40]、CKS-EWFC-F[26]、PFSCM[14]、kSDC[13]、MoG[23]、RGMM[22]和EWMM[3]算法与提出的算法进行了实验比较. 使用PCA 方法对灰度图像进行特征提取,其中CIFAR-10、CIFAR-100、MNIST 与Fashion-MNIST 图像数据的特征数均置为500;对于USPS 图像数据直接使用所有的灰度值,实验结果如表2所示,其中每个数据集所对应的三行数值分别为Acc、NMI和RI指标.
由表2 可知,对于选取的图像数据集,算法SEWMM 的聚类指标值优于EWMM 算法;与其他聚类算法相比,总体上来说,算法SEWMM 的聚类性能优于所比较的算法,例如,对于Fashion-MNIST 数据集,算法SEWMM 的Acc、NMI与RI指标值分别为0.5880、0.6139和0.8836,而EnSC 算法的相应指标值分别为0.5777、0.6087 和0.8935,可以看到,提出的算法在Acc 和NMI两个指标均获得了较高值,而EnSC在RI指标上获得了较高值,但SEWMM 与EnSC 两种算法的RI 指标值相差幅度不大. 总之,在提出的算法中,通过引入结构α-熵,调整参数α的取值,提出的算法能够获得更好的聚类性能.
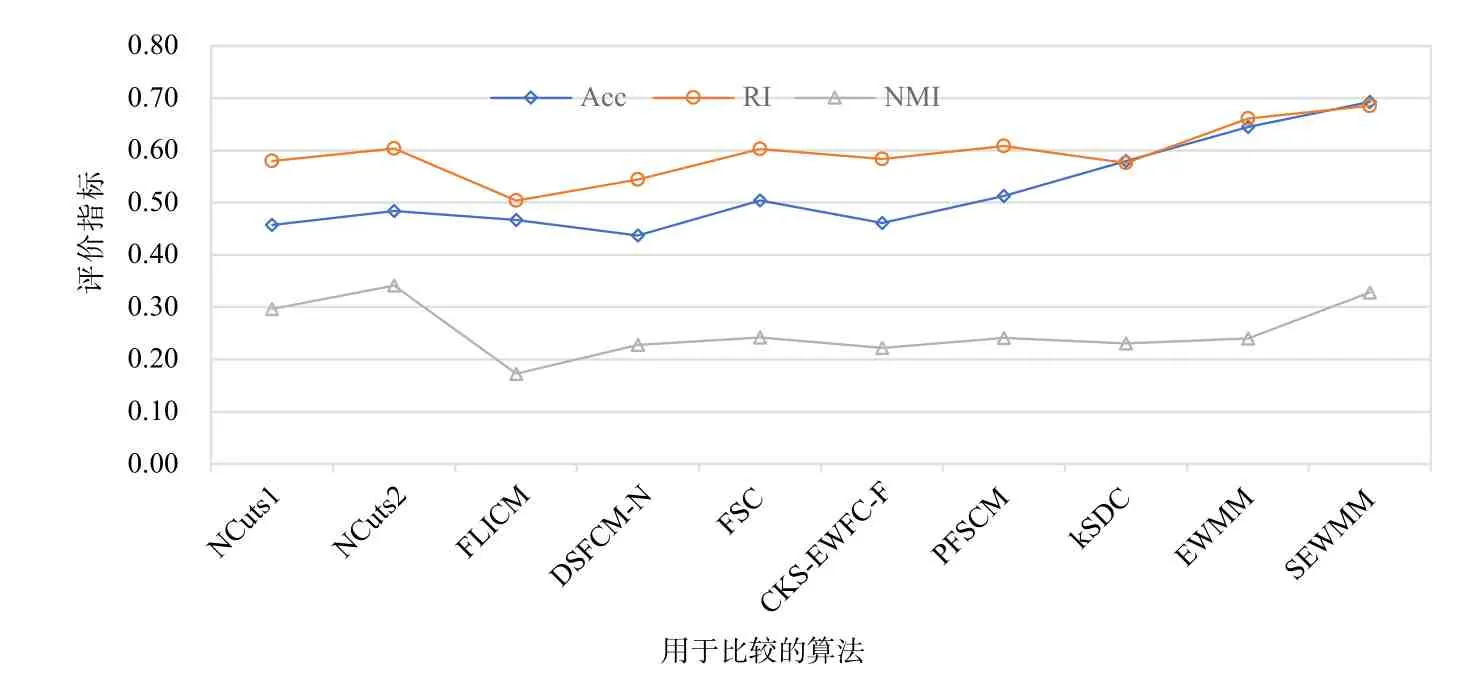
图1 图像分割实验结果
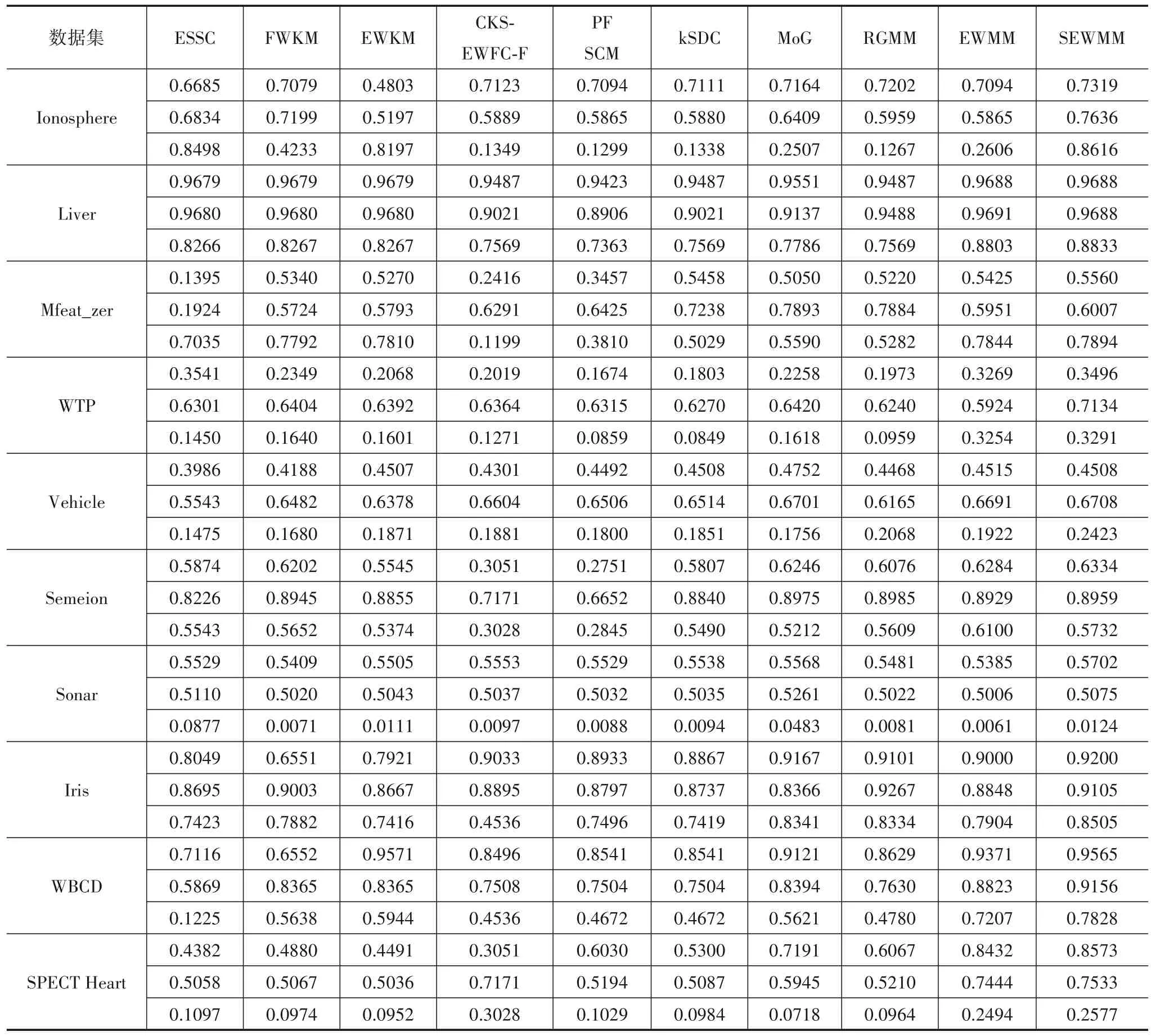
表1 不同算法在UCI数据集上的聚类性能比较
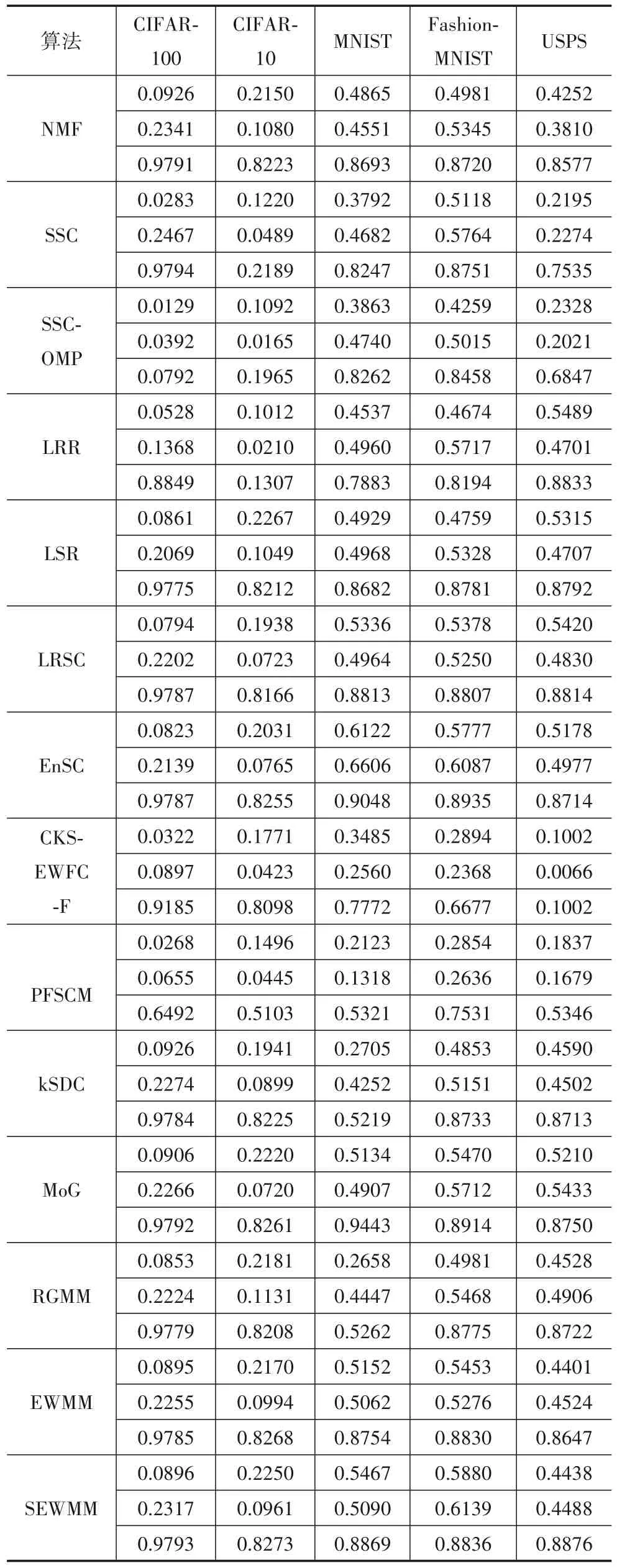
表2 不同算法对图像数据集的聚类性能比较
6 结论
本文在定义簇结构熵与聚类结构熵的基础上,将权向量的负结构α-熵引入到高斯混合模型中,提出了结构α-熵的加权高斯混合模型的子空间聚类算法SEWMM. 通过选取聚类正确率Acc、兰德指数RI 与标准互信息NMI 评价指标,在UCI 数据集与图像数据集上,对提出的算法进行了实验研究. 实验结果表明,与已有的子空间聚类算法相比,算法SEWMM 对数据的聚类效果更好. 同时,算法SEWMM 的提出也为大数据背景下数据的聚类提供了一种新方法.

