基于滑动窗滤波与卡尔曼滤波的信息融合

黄金虎 乔 祁

（1、中国直升机设计研究所，江西 景德镇 333001 2、中航技进出口有限责任公司，北京 102600）

1 总体设计思路

本文以无人直升机活塞发动机的转速信息融合为研究对象，具体实施过程如图1 所示。首先分析发动机的开车数据，建立对应的离散化数据模型；其次是确定初始参数、融合过程；最后分析对比融合数据与原始数据。

图1 设计流程图

活塞发动机的转速信号主要包含三路传感器采集，分别是频率采集单元（脉冲信号）、发动机采集单元TCU（数字信号）、旋翼转速信号（脉冲信号）。本文最终目的是在飞控计算机内具备实时融合三路传感器为一路，同时如果有一路信号出现故障时，能自动剔除该信号。

三路传感器的之间相互独立，额定转速5500rpm，旋翼转速乘传动比9.524，完整开车转速信号数据如图2 所示，离合器啮合后，旋翼转速与发动机转速重叠。在时间t=515～1672s 区间，发动机转速处于额定闭环控制状态。在时间t=1672～1900s 区间，发动机转速处于停车过程。

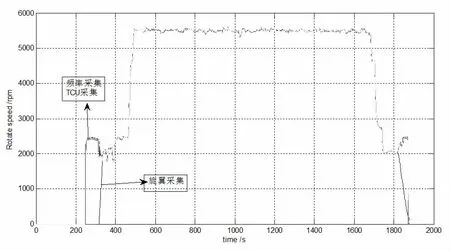
图2 各路信号数据

2 建立数学模型

发动机转速特性离散化的模型及观测模型如下：

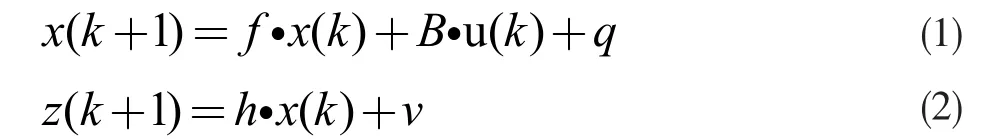
式中：x 为发动机的转速函数，k 为时间计数，f 为状态转移矩阵，B 为控制输入矩阵，μ 为外部输入包括油门开度、扭矩、活塞缸空气输入、环境温度等，q 为发动机本身系统偏差造成的高斯噪声，包含缸体振动、气动负载变化、油品、其他环境因素等。z 为各传感器的观测值包括发动机转速传感器（脉冲信号）、TCU 采集、旋翼传感器（脉冲信号），h 为转速到传感器映射矩阵，v 为各传感器采样时的高斯噪声。

3 窗空间

窗函数在信号处理中是指一种除在给定区间之外取值均为0 的实函数。本文借鉴此类方法，对有限时间范围的波形进行分析。本文的运算周期tick=40ms，建立一个按照先进先出原则的样本分析窗空间speed。其中speed 为13×3 矩阵，每列分别对应于频率采集单元（脉冲信号）、发动机采集单元（数字信号）、旋翼转速信号（脉冲信号）数值。

4 滤波参数的初始化

发动机的输入矩阵为μ，设μ1 为油门值、μ2 为扭矩负载值、μ3 活塞缸空气输入、μ4 环境温度等，则外部输入向量为μ=[μ1，μ2, μ3，μ4]T，发动机转速函数为x(μ1，μ2, μ3，μ4)，则控制阵B 为：

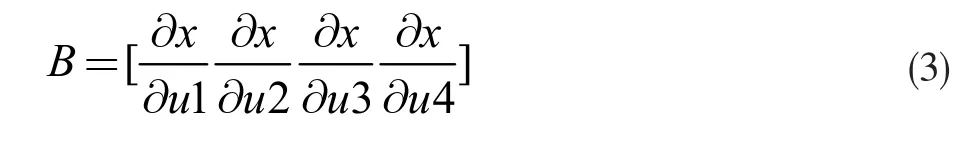
分析完整的开车时间历程数据，发动机在额定状态下，转速近似一条水平直线，即宏观上发动机转速对任意输入的偏导数为0，则控制矩阵为0。实际上，采用了PID 闭环控制的活塞发动是一套稳定的总距随动控制系统。在额定工况下，发动的转速，在任意负载下，转速的波动范围为（-50，50）。引起此类偏差是由发动机气缸特性、气动负载、油品、环境造成的，属于高斯噪声；如果想提高模型的预测准确性，实际使用中可通过黑盒法辨识出发动机转速模型，本文不做扩展。实际上对于机械惯性系统，在很短的时间的微小输入都可以看作是噪声干扰。因此公式(1)可以简化为：

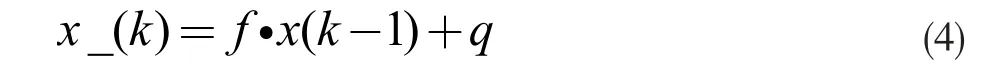
式中：带下标x_(k)为转速在本次tick 的先验估计值，x(k-1)为上次tick 的转速后验估计值(最优估计)，f 为状态方程。

4.1 状态方程f：在一个tick=40ms 下，默认状态下，上一tick 的采样与本次tick 的采样相同，转速不变，f=1。

4.2 过程噪声q:分析历程数据，得到模型高斯噪声q=1.5。

4.3 估计值协方差p：初始化p=1，需要迭代过程实时跟新。

4.4 先验估计协方差p_：初始化p_=1，需要迭代过程实时跟新。

4.5 窗空间列方差v：初始化v=[0 0 0]，用于存储speed 每列的方差，不断更新观测方程的方差矩阵。

有时候我们在材料上找不到明确的主题或标题，而问题设问上也没有具体对象的限制。那么我们可能遇到了“全开”式论题，我们只能根据材料信息，将零碎的信息源整合成一个对象，以此为基础进行“要义”式、“推因”式或“推果”式立论。若是零碎的材料信息可以整合成两个对象，可以考虑在二者之间建立联系，使之成为简约句子结构的主语或宾语。下面请看例3：

4.6 测量噪声协方差r：初始化r=[1 0 0;0 1 0;0 0 1]; 3×3 矩阵，用于求取测量残差，需要使用v 对对角线赋值，由于各传感器相互独立，因此其他元素赋值0。

4.7 观测矩阵z：初始化z=[0;0;0]; 1×3 的列向量，z1、z2、z3 分别对应频率采集单元（脉冲信号）、TCU（数字信号）、旋翼转速信号（脉冲信号）最新数值。

4.8 观测到状态矩阵h：由公式2 得，h=[1;1;1]，是1维列向量，用于映射传感器测试量与预测值，统一它们的量纲。

4.9 转速最优估计x：初始化x=0。

4.10 滤波增益矩阵K：初始化K=[0 0 0]，需要迭代过程实时跟新。

5 迭代运算

融合的迭代运算主要以卡尔曼滤波[2]的为基础进行，但系统噪声及观察噪声做了相应调整。

5.1 卡尔曼第一公式

式中：状态转移公式x_是本次的先验估计，f 是状态转移矩阵，x 是上次的最优估计。

5.2 卡尔曼第二公式

式中：噪声协方差矩阵的传递公式，预测模型带来的噪声q，表示不确定性在各公式的传递。

5.3 人工干预通道

为了避免矩阵计算机运算过程中出现非法数，需要对窗空间的各列向量均方根值v 做出限定。设定上边界v(1)Max=25000,v(2)Max=25000,v(3)Max=25000。

设定下边界，使用抛物线函数，对称轴由实际开车均方根值数据得到。极小值可人工设置，本文称之为“人工干预通道”，通过调整各传感器极小值来主动选择置信度，极值越小置信度越高。

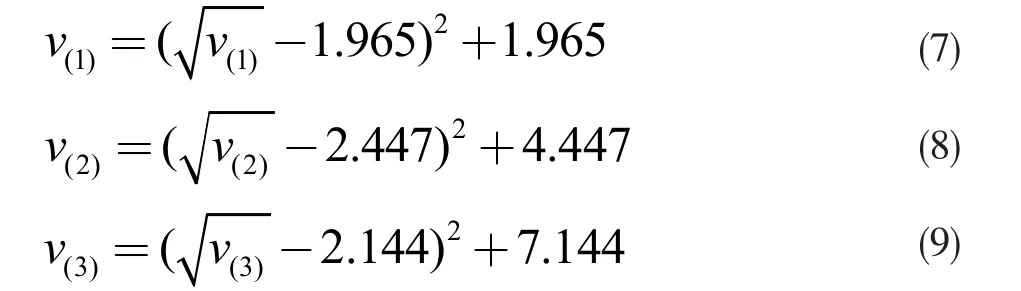
5.4 余度管理与控制

当某路传感器出现背离其它传感器信号时，采用三判二的原则，方差v 赋极大值，能使其融合权重占比降至最低。

5.5 测量残差协方差

5.6 卡尔曼第三公式

卡尔曼系数的更新，其中K 为1×3 的列向量，每个元素对应的数学意义分别表示频率采集、TCU 采集单元、旋翼转速采集在转速融合中所占之权重。预估值在转速信息融合中所占权重则为1-K×h。

5.7 卡尔曼第四公式

后验估计（最优估计）=模型数据后验估计+k×（观测残差）。

5.8 卡尔曼第五公式

预估模型的噪声协方差矩阵的更新。

5.9 窗空间的更新

程序等待一tick 后，更新speed 的13×3 的矩阵，以最新的转速采样z1k+1、z2k+1、z3k+1替换上一tick 的值，队列其他元素依次向前，z1k-12、z2k-12、z3k-12丢弃，按照“先进先出”的原则往前替换，如公式16、17 所示。

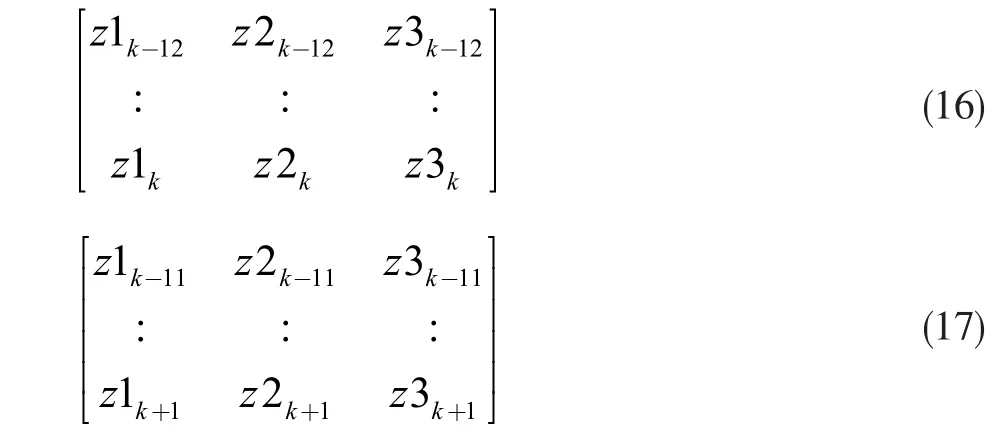
求取k+1 时刻speed 的每列均方根值，更新窗空间方差v，用于不断校准观测方程的方差矩阵。程序跳转至卡尔曼第一公式。

6 融合效果与分析

飞控计算机分别记录下k 矩阵，转速融合最优估计x，画图分析如下。

6.1 额定阶段的转速与权重

选取时间段（1015～1050s）波动最大部分分析，如图3所示。

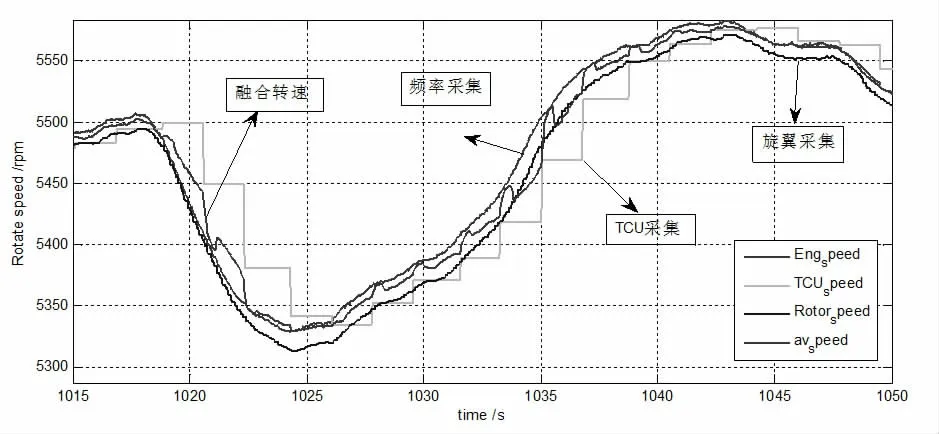
图3 额定阶段采样值与融合值

k1、k2 、k3、k4 分别表示频率采集、发动机采集单元、旋翼转速采集、预估值在转速信息融合中所占权重。其中k1+k2+k3+k4=1。在发动机额定状态，频率采集的权重约50%，TCU 采集的权重约12%，旋翼采集约18%，预估值的权重约20%。这些值的置信度可以通过调节人工干预通道进行调节。当某一信号波动较大时，与之对应的占比将相应的自动降低如图4 所示。

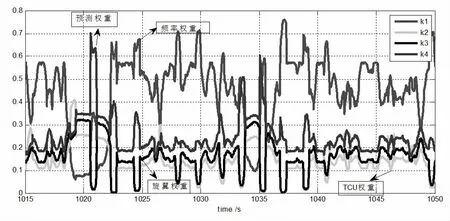
图4 额定阶段权重对比

6.2 停车阶段的转速与权重

选择时间t=1672～1900s 区间，分析发动机停车的过程数据如图5 所示，离合器率先进行脱开的过程，旋翼转速下降，最后发动机停车。

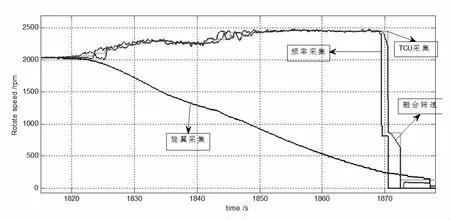
图5 停车阶段采样值与融合值

发动机的停车过程，能模拟当旋翼传感器失效时，融合算法经过若干步长后，能有效剔除失效信号。信息失真度低。如图6 所示，旋翼转速在最终融合过程中权重被调节到0%。

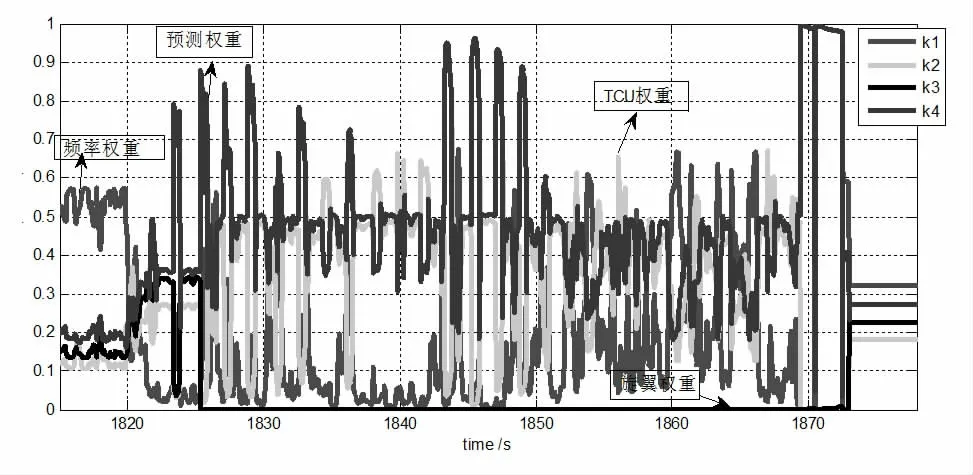
图6 停车阶段权重对比

7 结论

本文基于卡尔曼滤波的预测与跟新的回归校准思想，引入了谱分析中窗函数概念，改进了常规的“三判二”式的信号选择方式，设计了一套既能满足时域离散系统、过滤信号中高斯噪声的，又能诊断并屏蔽失效信号的、具备人工干预、余度控制融合的方法。