多层合采油藏废弃井网取热性能评价

宋先知 许富强 姬佳炎 石 宇

1.油气资源与探测国家重点实验室·中国石油大学（北京） 2. 西南交通大学地球科学与环境工程学院

0 引言

与太阳能、风能和潮汐能等其他可再生能源相比，地热能具有地域分布广、资源量大、清洁环保和热能连续性好等优势。含油气盆地中蕴藏丰富的中低温地热资源，全国12个主要沉积盆地地热资源量为2.5×1022J，折合标准煤8 531.9×108t，其中，可开采资源量为7.5×1021J，折合标准煤2 560×108t[1]。油田地热是地热资源的重要组成部分，在油田聚集的松辽盆地、渤海湾盆地和鄂尔多斯盆地均发现较高热流值[2]。油田地热可进行发电、供暖、油田伴热开发和农业养殖等利用[3-4]，发展潜力巨大。

在中深层地热开发过程中，钻井成本超过总成本的二分之一[5]，成为限制中深层地热应用的主要因素。油田经过长期开发，采出液含水率显著上升，部分老油田含水率甚至超过95%[6]，原油产量下降致使油井经济效益降低。当油井效益超过经济极限，将会被停产甚至废弃。目前，全球有2 000×104～3 000×104口废弃井[7]，我国油田废弃井总数早已突破数十万口。将废弃井改造为地热井可显著降低钻探成本和封井处置成本，同时有效解决废弃油井污染问题[8]。国内已有废弃井转地热井的相关研究，如大庆油田开展废弃井修井、地热资源评价及现场应用，华北油田在留北潜山油藏开展地热综合利用，大港油田开展报废油井改地热井评价及应用，辽河油田提出废弃井改造的成井方式并进行开采/回灌试验测试等[9-10]。2022年，美国能源部（U.S. Department of Energy）对该国4个项目资助840万美元，研究从废弃油气井中取热以进行供暖或发电应用，同时利用油气行业劳动力和基础设施进行地热能并网[11]。上述研究的开展有力地证明了油田废弃井取热的可行性和广阔前景。

现有废弃井取热方式多为单井闭式取热或直接泵取地下水取热，前者取热效率低，后者易造成地下水位下降，废弃井网取热则可有效弥补上述不足。目前国内外虽有废弃井网取热项目，但储层内流动传热特征尚不明确[9]。有学者分析了不同孔渗、不同注入条件下的储层温度场分布特征[12-13]，但研究仅限于注采井周附近或未考虑储层不同层位孔渗特征差异，并且多未考虑层间干扰对取热性能的影响。而多层砂岩油藏的地热储量和产量均约占我国总量的50%，该类油藏储层物性纵向差异明显[14]。由于层间非均质性影响，多层油藏注水开发过程中普遍存在层间干扰问题[15]，对油田取热将产生较大影响，亟需开展多层合采含油热储取热性能评价。为此，笔者以枯竭油藏（可扩展至高、特高含水油藏）为研究对象，考虑油水两相和层位差异，开展了含油热储不同层位不同孔隙度、渗透率和初始含油饱和度下生产温度、注采压差及层间干扰对比，分析了层间干扰对取热性能的影响。研究成果对制定含油热储高效取热方案具有一定的指导意义，有助于油田地热的高效开发与推广利用。

1 数学模型

含油热储存在油水两相，两者在热储中流动，同时与岩石基质换热。本文建立的油水两相热流耦合模型主要基于以下假设：①岩石基质水平渗透率为垂直渗透率的10倍[16]，储层孔渗物性远高于盖层；②岩石物性为常数，即不随温度和压力改变；③传热只考虑对流传热和热传导，忽略热辐射过程；④模型采用局部热平衡假设；⑤储层压力高于泡点压力，即储层中只存在油水两相且两相均为不可压缩流体。

油相、水相质量守恒方程为：

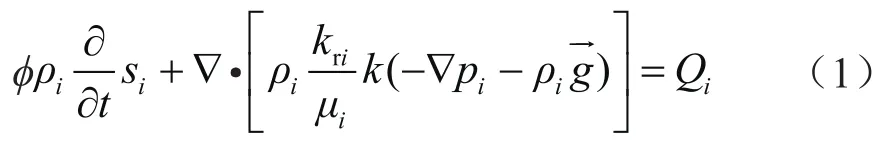
式中φ表示孔隙度；ρi表示第i相的密度，kg/m；t表示时间，s；si表示第i相体积分数；kri表示第i相相对渗透率；μi表示黏度，Pa·s；k表示渗透率，m2；pi表示第i相压力，Pa；Qi表示第i相质量流量，kg/(m3·s)。

储层流体包含油—水两相，两相饱和度存在以下关系：

式中sw、so分别表示水相、油相饱和度。

水相为润湿相，油相压力和水相压力存在以下关系：

式中po、pw、pc分别表示油相、水相、毛细管压力，Pa。

传热方程存在以下表达式[17]：

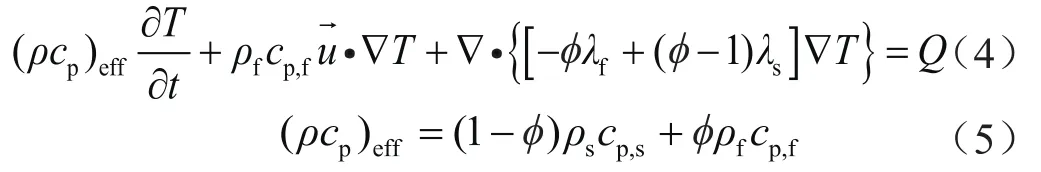
式中 (ρcp)eff表示恒压下有效体积热容，J/(m3·K)；ρf、ρs分别表示混合流体、岩石基质密度，kg/m3；cp,f、cp,s分别表示恒压下混合流体、岩石基质比热容，J/(kg·K)；表示流体速度，m/s；Q表示热源，W/m3；λf、λs分别表示混合流体、岩石基质热导率，W/(m·K)。

根据前人研究结果[18]，通过加权平均，可以得到混合流体的物性参数如下：

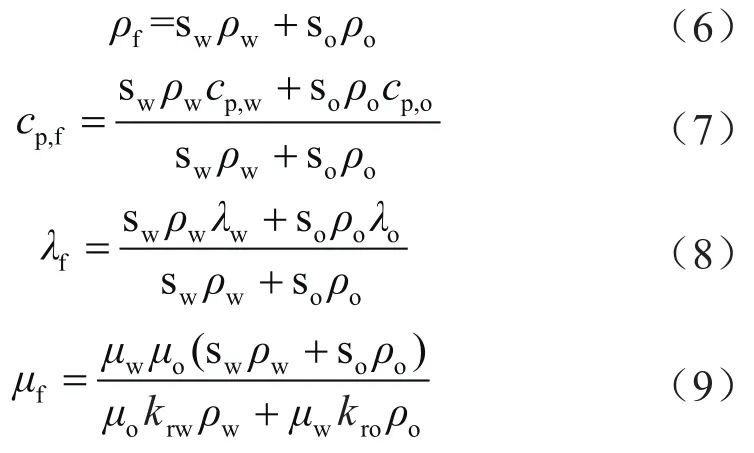
式中ρw、ρo分别表示水相、油相密度，kg/m3；cp,w、cp,o分别表示恒压下水相、油相比热容，J/(kg·K)；λw、λo分别表示水相、油相热导率，W/(m·K)；μf、μw和μo分别表示混合流体、水相、油相黏度，Pa·s；krw、kro分别表示水相、油相的相对渗透率。

水相为主要换热工质，水相密度、比热容和热导率随温度变化[19]，具体物性参数表达式如下：

油相密度设置为850 kg/m3，比热容为2234.2 J/(kg·K)，热导率为0.156 W/(m·K)，油相、水相黏度如表1所示，油相和水相相对渗透率及毛细管压力如表2所示，部分参数设置参考了本文参考文献 [13,20]中的数据。

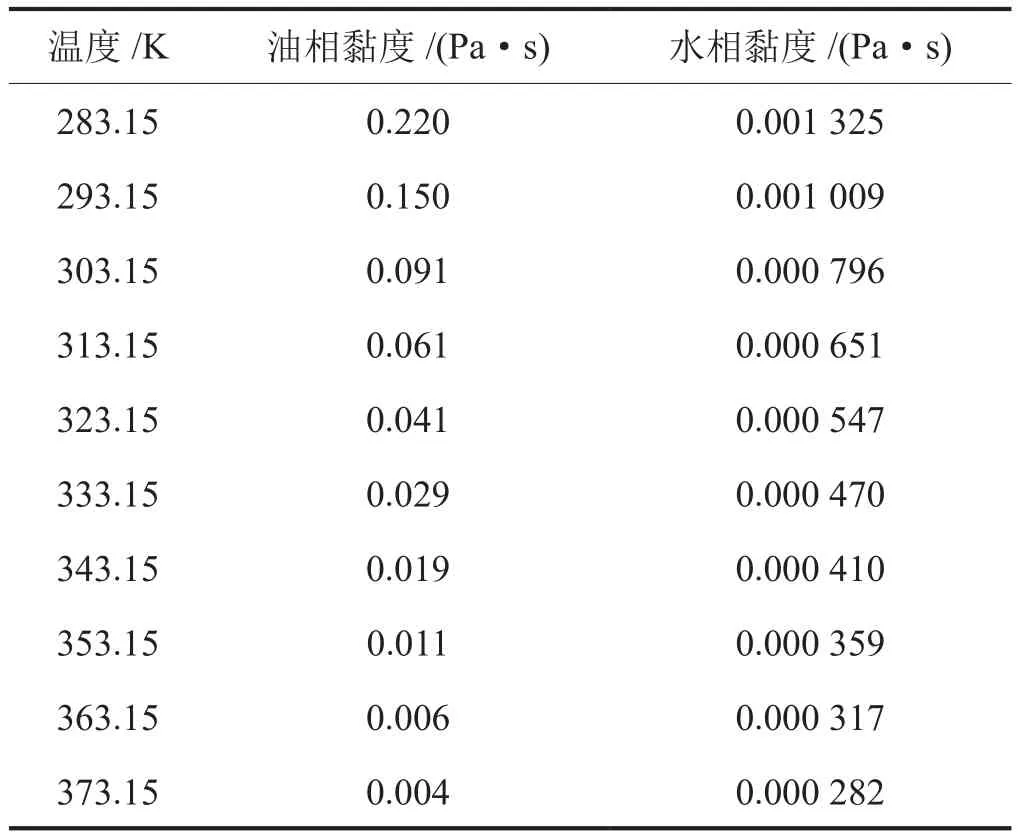
表1 油相和水相黏度表

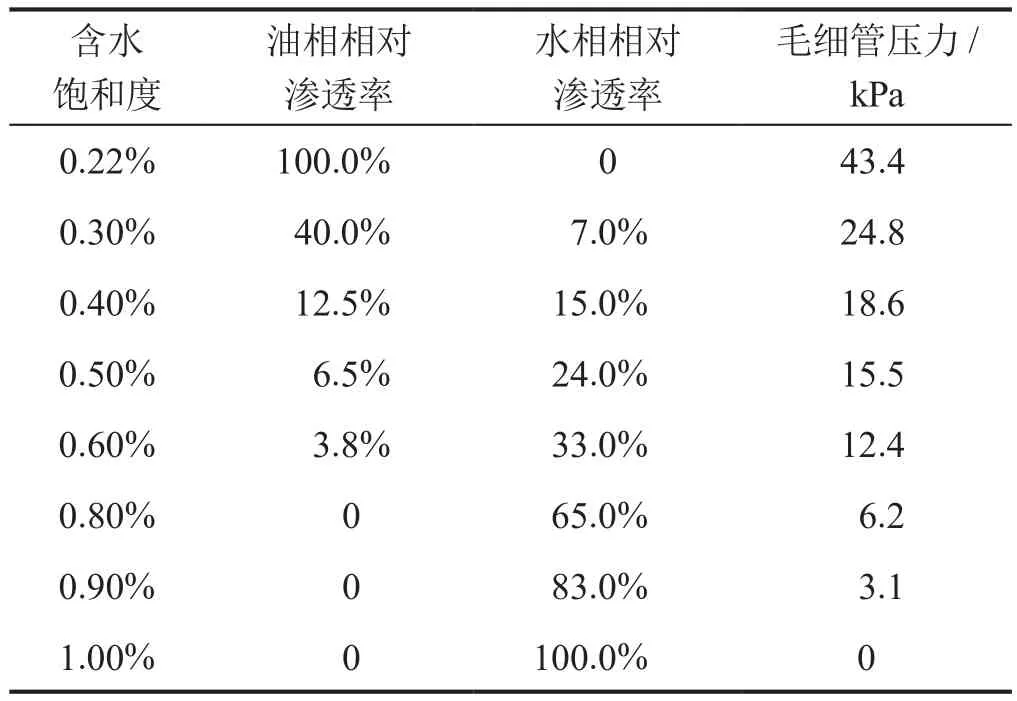
表2 油相和水相相对渗透率及毛细管压力表

采用各储层段的平均生产温度和平均注采压差对比各层的取热性能，其中，平均生产温度定义为各层位生产井生产温度的平均值，表达式如下：

式中Tout表示平均生产温度，K；l表示各储层小段生产井长度，m；L表示各储层段生产井长度，m。

平均注采压差定义为各层位注入井压力与生产井压力的差值，表达式如下：

式中Δp表示平均注采压差，MPa；pin、pout分别表示注入井、生产井平均压力，MPa。

2 数值模型

分层含油热储几何模型计算区域为1 500 m×1 500 m×1 500 m（图1）。储层被盖层包围，自上而下共分为5层。油藏储层单层厚度一般为几十米，然而较小厚度下层间温差小，不便于结果分析。为研究长期取热下层间干扰规律，本文将每层厚度设置为100 m。后文也将对比不同类型薄层热储的取热性能，用以验证本文规律的普适性。储层孔隙度和渗透率远高于盖层，两者物性参数见表3。注入井和生产井分别使用蓝点/线和红点/线表示（图1-a、b），长度均为500 m，注入井和生产井的井径分别为0.152 4 m、0.139 7 m。在油藏生产后期，常通过加密井网方式提高原油产量，而在废弃井取热中，并非所有注采井均被用于改造，为模拟不同排距和井距，本文设置注采井距分别为150 m、250 m、200 m和200 m（图1）。

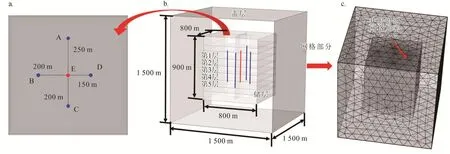
图1 含油热储模型计算区域图

表3 储层和盖层物性参数表

模型侧边界均为恒温边界，并将其温度设置为储层初始温度，上下边界均为绝热边界，所有边界均设置为无流动边界，模型顶部温度和压力分别为333.15 K和20 MPa，地温梯度和压力梯度分别设置为0.03 K/m和10 000 Pa/m[19]。注入井采用流量入口，各注入井流量均设置为12.5 kg/s，生产井采用压力出口，各层生产压力低于该层初始平均地层压力2.0 MPa。注入流体温度为303.15 K，储层束缚水饱和度和残余油饱和度分别为0.22和0.20，初始含油饱和度设为0.30，盖层只存在水相。

在储层顶面划分三角形网格，在井眼附近进行加密处理，以储层顶面为源面、储层底面为目标面对储层计算区域进行扫掠，形成三棱柱单元。最后剩余区域进行自由网格四面体剖分，计算区域网格剖分见图1-c。选取生产井平均温度作为网格无关性评价指标，在生产10年后对5种不同网格下的该温度值进行对比，研究得出当单元数达到12.9×104，对应自由度达到44.5×104时，计算结果趋于稳定，综合考虑计算精度和求解效率，使用该网格剖分方案作为最终方案。另外，相对容差的设置对取热性能也存在一定影响，以生产10年后生产井中心点处温度作为评价指标，对比了 10－5、10－4、10－3、10－2共4种不同相对容差下的该点温度。结果表明，当相对容差值接近10－4时，温度趋于稳定，考虑到求解精度和效率，所有变量相对容差设置为 10－4，并视为收敛标准。模型总体计算时间为20年，计算步长为1天。

本文将油水两相视为混相与岩石基质进行换热，温度场与流场进行耦合时，本质是单相（混合物）参与换热，利用COMSOL软件开展热流耦合研究已经得到了广泛的验证[21]。所以本文关键在于验证两相流模型的准确性，为此与已有文献[20]研究数据进行了对比。该文献[20]采用多种软件对相同算例进行模拟计算，本文选取其某一算例的计算结果平均值进行验证，所有模型设置均参考上述文献[20]。验证结果表明，最大绝对误差出现在初始时刻达24.93 m3/d，最小绝对误差仅为0.30 m3/d，在研究时间内（1 400 d）平均绝对误差为4.51 m3/d（图2）。在使用其他软件进行求解时也存在类似误差且初始时刻误差较大，原因在于不同软件的求解方式不同[20]。但由图2可知，随着生产进行，绝对误差呈下降趋势，所以认为本文所建模型是可靠的，可用来模拟含油储层两相流热流耦合过程。

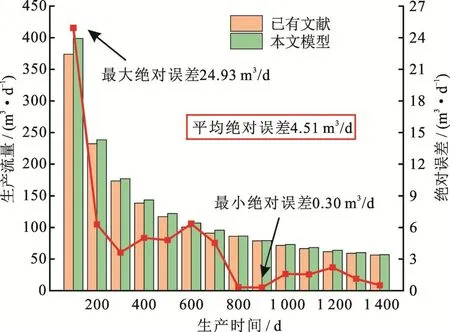
图2 本文模型计算结果与已有文献[20]研究结果对比图

3 结果分析

3.1 算例设置

采用控制变量方法，分别研究不同孔隙度、渗透率和初始含油饱和度储层的取热性能。孔隙度和渗透率间存在一定的关联，但本文旨在进行不同孔渗条件下分层合采油藏的取热性能对比，所以在研究不同孔隙度和渗透率条件时，将两者单独考虑，即忽略两者间的关联。另外，考虑到地层沉积过程中的压实，所以在算例设置中，渗透率和孔隙度自上而下逐渐降低，如表4所示。初始含油饱和度分层设置求解较难收敛，将储层设置为初始含油饱和度不同的含油均质储层进行对比研究，设置6种不同算例（表4）。特别说明的是初始含油饱和度为0、20%和30%的储层分别对应纯水储层、无油相流动储层（初始含油饱和度等于残余油饱和度）和基础算例储层。

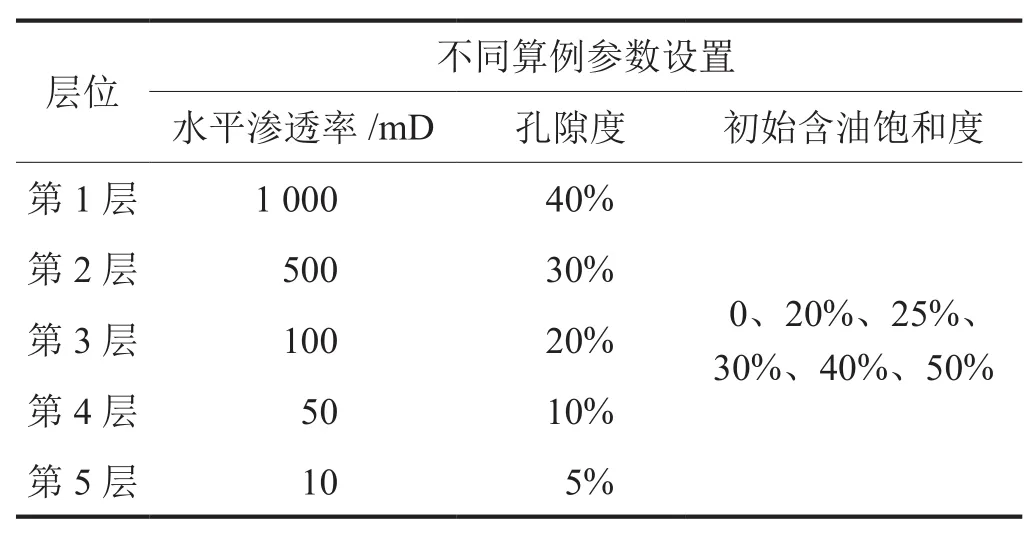
表4 不同算例研究参数设置表

3.2 不同初始含油饱和度储层

首先，分析基础算例储层温压特征并与纯水均质储层进行对比，作为其他算例对照组。基础算例储层自上而下分为5层，渗透率均为100 mD，孔隙度均为20%，初始含油饱和度设置为30%，纯水均质储层除初始含油饱和度为0外，其他设置均与之相同。图3、4分别为基础算例储层不同时刻温度场及20年后储层开采段压力场分布。由图3可知，温度场“冷锋”自上而下倾斜，原因是不同层位流体的注入量近乎相同且注入温度相同，由于地层存在地温梯度，所以上部储层温度低于下部储层，当流体与储层基质进行换热时，流体从储层吸收热量，该过程中低温储层层位温度下降速度将快于高温储层层位，所以上部更易发生热突破。此外，井间距越小，热突破时间越早，该规律在以往研究中已得到广泛证明。由图4可知，同一层位最大和最小压力分别出现在注入井和生产井附近，呈现明显的“压力漏斗”形态，图中字母分别代表不同注入井和生产井并与图1对应。

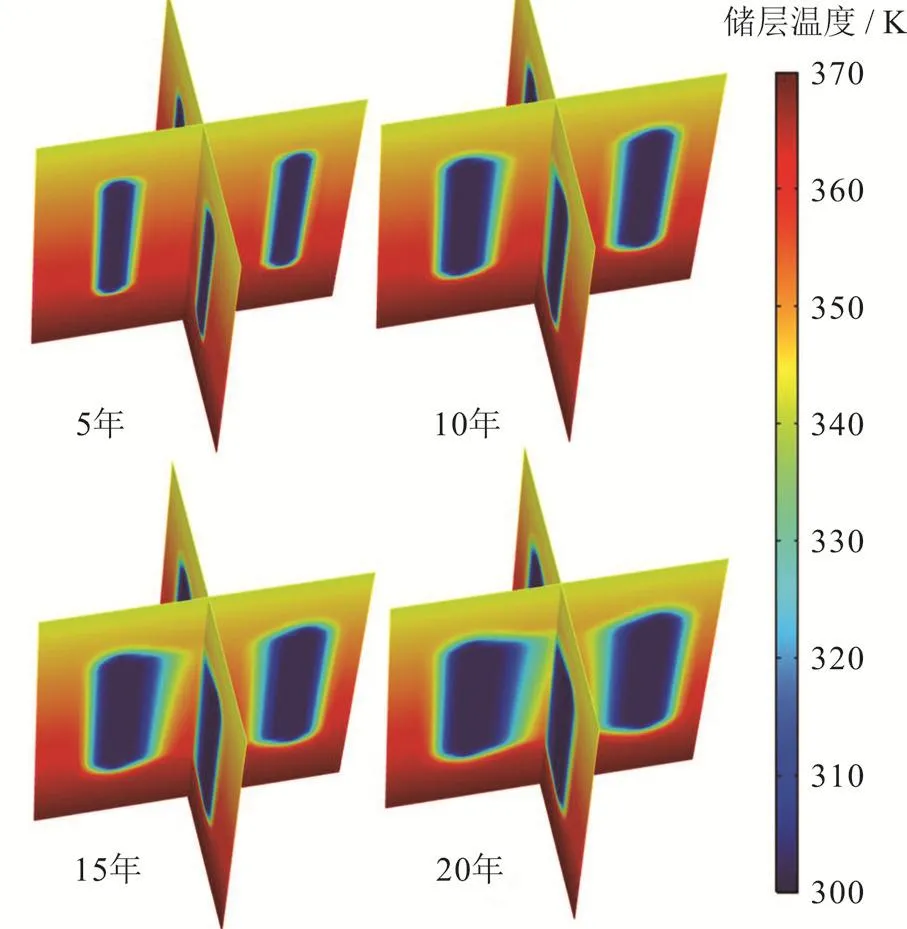
图3 基础算例储层温度场随时间变化图

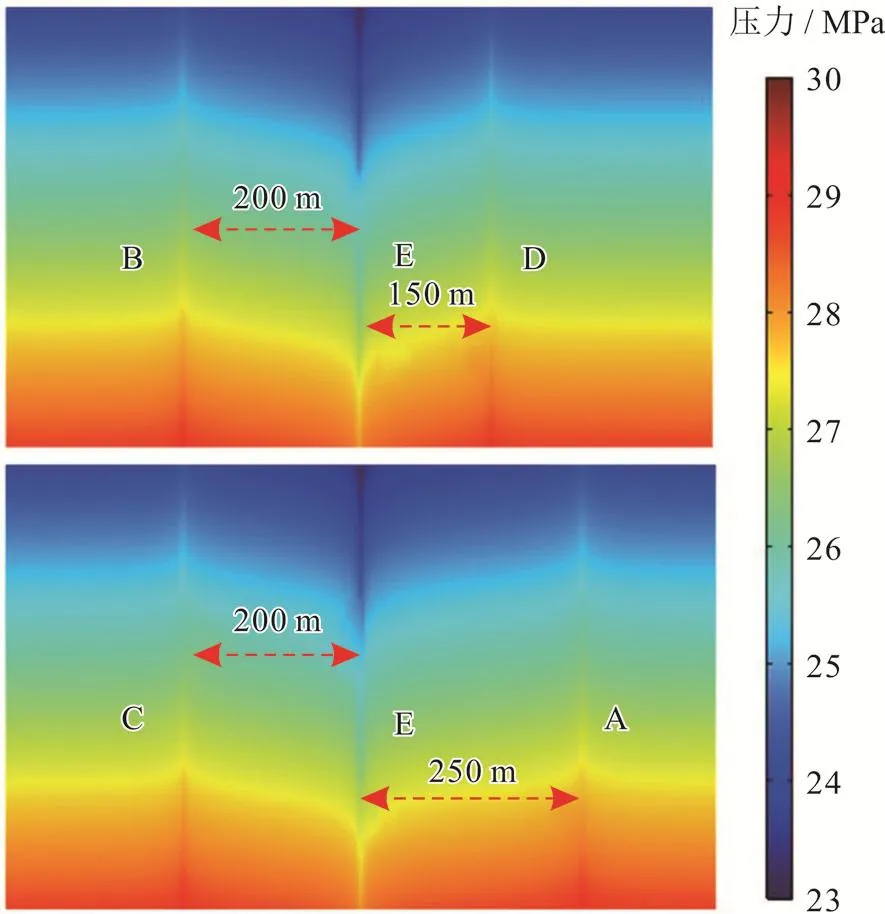
图4 生产20年基础算例储层开采段压力场分布图

为定量分析不同层位生产特征，依据图1层位划分方式，分析基础算例储层和纯水均质储层5个层位注采压差和生产温度随时间的变化规律（图5）。如图5-a所示，由于温度梯度存在，基础算例储层初始时刻第1层和第5层温差为12.0 K，生产20年后，温差为12.2 K，差值变化并不明显。随着开发进行，各层生产温度逐渐下降，导致流体黏度上升，注采压差逐渐上升。由图5-b可知，基础算例储层第5层注采压差始终低于其他4个层位，最大差值达0.27 MPa，原因为底部储层温度高、流体黏度低、流动阻力小、注采压差小。

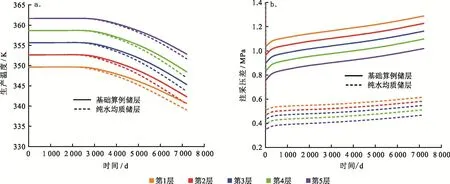
图5 基础算例储层和纯水储层不同层位生产特征随时间变化图

纯水均质储层同样存在上述规律，就单层而言，纯水均质储层生产温度和注采压差均低于基础算例储层，生产20年后两类储层对应层位的差值分别约为2.0 K和0.6 MPa。两者注采压差不同原因为纯水储层流体黏度小，流动阻力小。为分析初始含油饱和度影响，对比了不同含油饱和度下的生产特征，见图6。初始含油饱和度越大，生产温度越高，原因为此时产出液油相体积分数较大，油相在初始时刻即赋存于储层当中，其温度与储层温度相同无需加热，所以生产相同质量的混合流体，储层热量消耗低。注采压差对初始含油饱和度变化较为敏感，20年后最大差值达到1.32 MPa，说明油相的存在可显著提升注入压力。

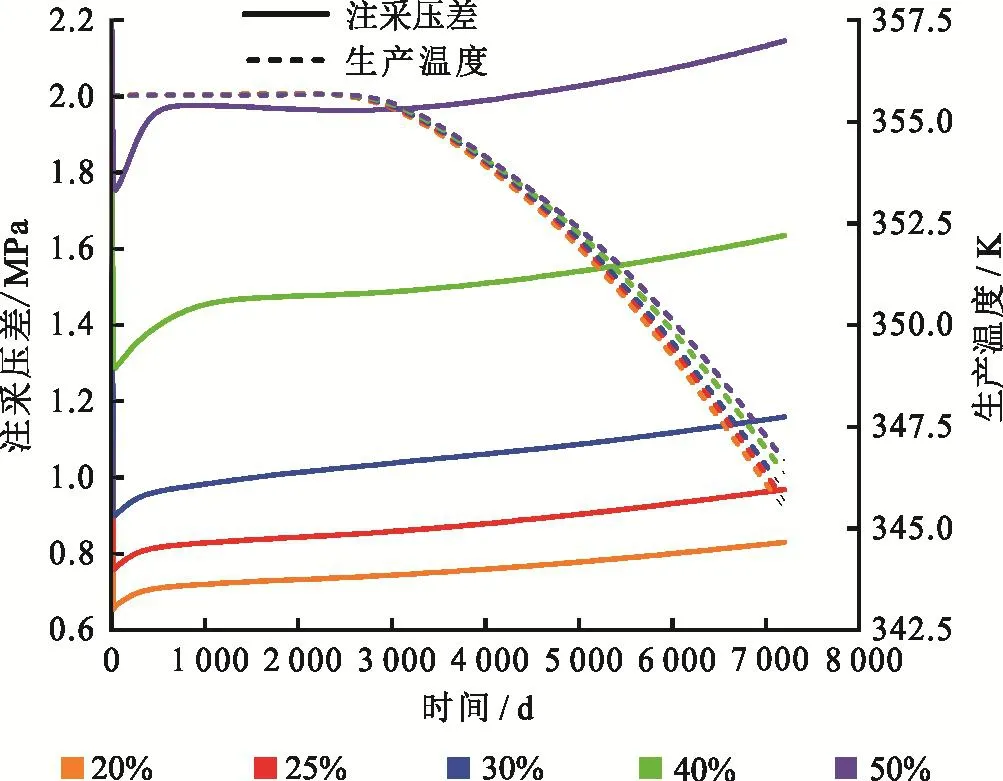
图6 不同初始含油饱和度生产特征对比图

3.3 不同渗透率储层

不同渗透率储层温度场随时间变化云图见图7，生产20年储层开采段压力场分布见图8。与均质储层相比，不同渗透率各层位温度剖面差异明显。如图7所示，开发10年后，高渗透第1层已发生明显热突破，其他储层冷温突进并不明显，开发20年后，高渗透第2层亦发生明显热突破。说明高渗透层位为流体流动主要层位，其生产井流体来自同层注入井和其他低渗透层，后文将具体分析层间干扰对取热影响。由图8可知，高渗透层注入压力远小于低渗透层注入压力，致使压力漏斗在储层下部更为明显。

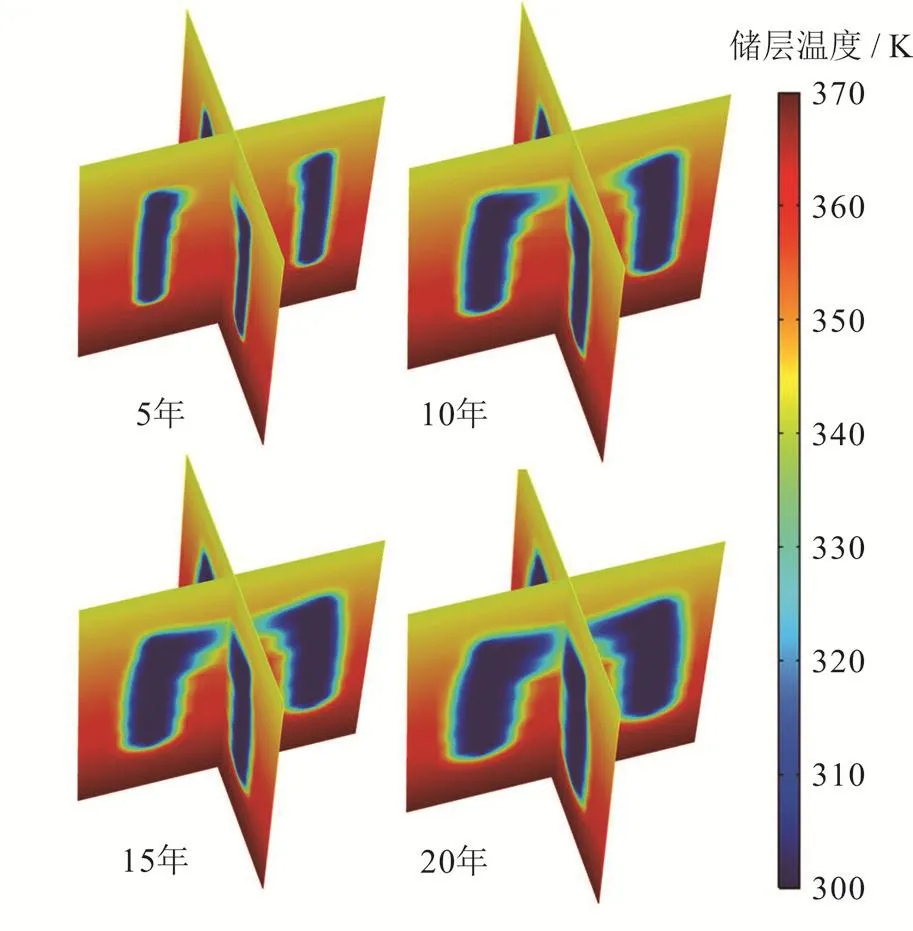
图7 不同渗透率储层温度场随时间变化图

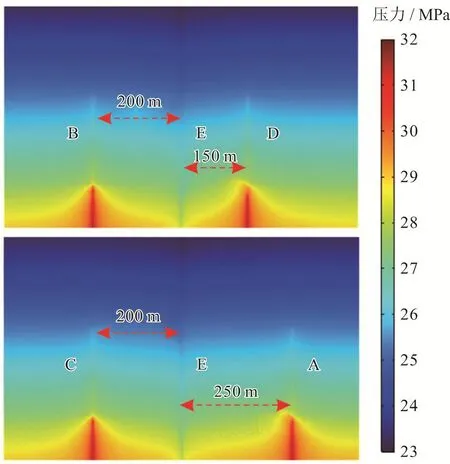
图8 生产20年不同渗透率储层开采段压力场分布图

同样的，依据图1层位划分方式，分析了不同渗透率储层5个层位注采压差和生产温度随时间变化规律（图9）。第5层注采压差最低，生产20年后与第1层最大差值可达3.27 MPa。各层最大温差为24.5 K，远大于基础算例储层温差值。说明渗透率为影响含油储层生产特征的主要参数，应当在开发中优先考虑该参数的影响。

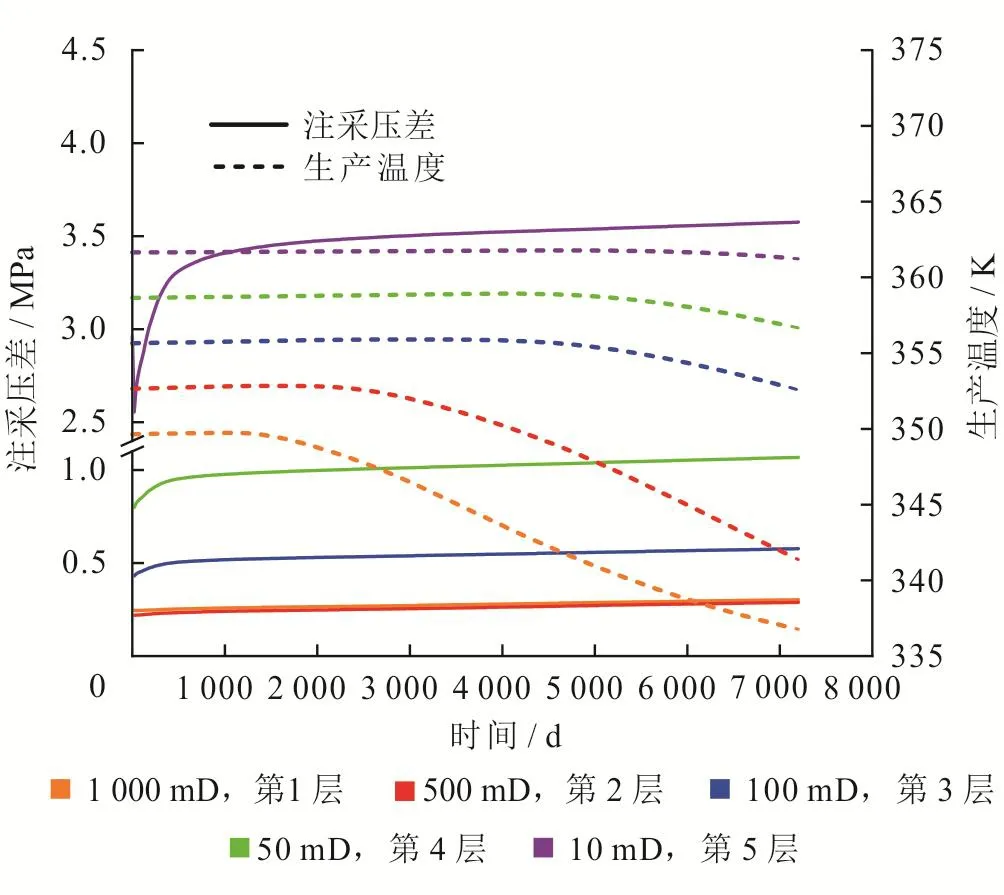
图9 不同渗透率储层不同层位生产特征随时间变化图

3.4 不同孔隙度储层

不同孔隙度储层不同层位生产特征随时间变化见图10。相较于基础算例储层，当孔隙度大于20%（基础算例储层孔隙度）时，生产温度高于基础算例储层对应层位温度，并且孔隙度越大差值越大。当孔隙度小于20%时，生产温度低于基础算例储层对应层位温度，并且孔隙度越小差值越大。主要原因为初始含油饱和度相同时，孔隙度越大，储层含油量显著提升，产出液中油相体积分数增大，油相初始时刻即存在于储层当中，无需加热，生产相同质量流体储层温度下降程度低，生产温度高。反之，孔隙度越小，生产温度低。孔隙度对注采压差的影响较小，可忽略不计。

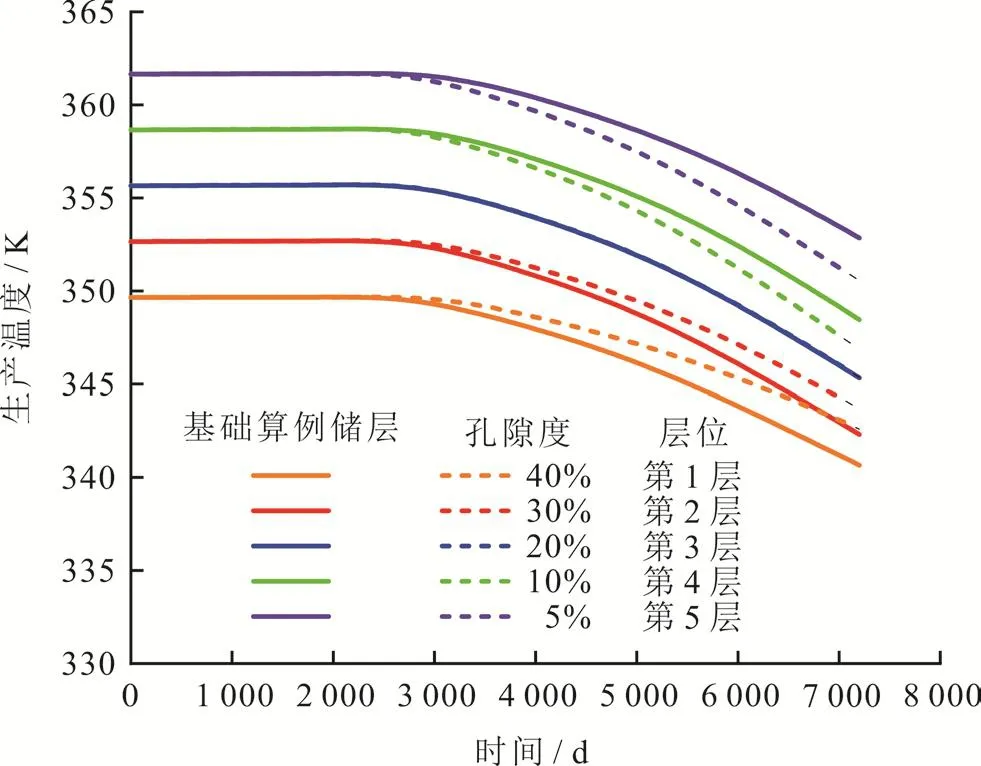
图10 不同孔隙度储层不同层位生产温度随时间变化图

3.5 层间干扰分析

流体在储层中并非仅存在水平流动，同时也存在垂向流动，不同储层不同层位产液量见图11。如不考虑层间干扰，则每层生产井流量应为10 kg/s，然而由图11可知，不同储层物性下，每层生产井产液量显著不同。基础算例储层层间干扰小于纯水均质储层，原因为油相存在导致混合流体黏度上升，流动性降低，垂向流动减弱。不同孔隙度储层与基础算例储层、纯水均质储层的产液量差值较小，不同渗透率储层与其他储层产液量差值明显。生产20年后不同储层不同层位的产液量见图12-a。不同渗透率下层间最大差值可达27.08 kg/s，其他储层的层间产液量最大差值均小于3.00 kg/s，说明渗透率为影响层间干扰的主要因素。

图11 不同储层不同层位产液量图

不同储层整体生产温度对比见图12-b。纯水储层生产温度低于基础算例储层和不同孔隙度储层。不同渗透率储层热突破时间较其他储层较早，而生产一段时间后，生产温度显著高于其他类型储层。以20年为例，与其他储层最大差值可达5.33 K。生产温度变化曲线与坐标轴所围面积反映了产热量大小，不同渗透率下20年的累计产热量明显高于其他类型储层。为更好地贴近实际储层，将单层储层厚度设置为20 m（薄储层），计算发现同样存在上述规律（图12-c）。说明在有边界热源补充的情况下，较强的层间干扰可以增大循环工质换热面积，强化换热过程，实现热储高效开发。层间干扰对油藏产油不利，而对枯竭油藏取热存在积极作用，说明了油藏产油和产热存在一定差异，也进一步证明了本文研究的必要性。

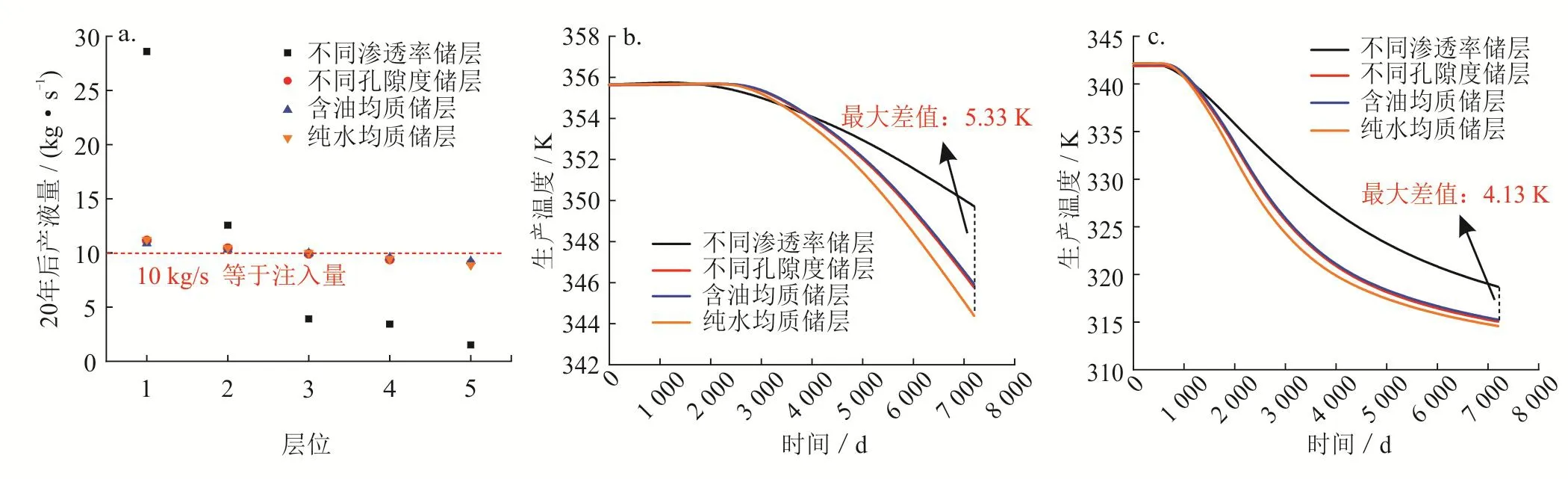
图12 不同类型储层整体生产温度及不同层位20年后产液量对比图

4 结论

1）含油均质储层不同层位生产温度和注采压差均高于纯水储层。初始含油饱和度越小，储层生产温度和注采压差越低，注采压差对初始含油饱和度变化较为敏感，20年后最大差值可达1.32 MPa，说明油相存在可显著提高注入压力。

2）不同渗透率储层不同层位生产温度和注采压差相差较大，高渗透层易发生热突破且注采压差较低，20年后与低渗透层最大差值可达3.27 MPa，最大温差可达24.5 K，远大于含油均质储层各层位对应差值，说明渗透率为影响含油储层生产特征的关键参数。不同孔隙度下不同层位生产温度和注采压差相差较小。

3）含油均质储层的层间干扰小于纯水均质储层，不同孔隙度储层与之相当。不同渗透率储层与其他储层差异明显，生产20年后不同层间最大产液量差值可达27.08 kg/s，较强的层间干扰增大了换热面积，最大可提高生产温度5.33 K。在有边界热源补充的情况下，层间干扰强烈的储层更易获得高取热量，在废弃井取热改造中可优先考虑此类储层。