基于代理模型的机身蒙皮复合材料夹层结构可靠性分析

丁振东, 李洪双, 管晓乐

1.南京航空航天大学 航空学院, 江苏 南京 210016；2.中国航天科工集团有限公司 北京动力机械研究所, 北京 100074

复合材料因其出色的可设计性和结构效率在航空航天领域被广泛应用。其中夹层结构是一种常见的复合材料结构形式，不仅可以在较小的质量代价下满足力学性能要求，特殊的设计还能使其具有隐身、隔热、降噪等多元化功能。然而，相较于传统的金属材料，复合材料力学性能的各向异性及对环境条件、制造工艺的敏感性较大，导致其结构性能呈现出较大的分散性。采用确定性分析方法难以准确地预测结构性能，容易造成性能过高或者过低。同时复合材料夹层结构功能的多元化也带来了多学科交叉和耦合问题，在传统的力学性能设计要求下可能增加热学、电磁学、声学等多学科问题。为了保证夹层结构系统的可靠性，这些因素在设计中需要更为系统化和全局化的考虑。

结构可靠性方法能够量化结构中的不确定因素影响，在确定性分析的基础上构造结构系统的极限状态函数，得到结构性能响应的统计特性和失效概率信息[1]，为准确地实现结构的设计要求和功能提供支持。复合材料夹层结构的可靠性分析往往有着以下特点：①多维随机变量，这是由其设计变量的复杂性和不确定来源的多样化决定的；②隐式化、高度非线性极限状态函数，这是由相应的力学有限元分析模型、声学模型等数值模型和极限状态确定的；③结构失效为小概率甚至极小概率事件，这对极限状态函数的全局计算精度和可靠性计算方法的效率提出了双重要求。

由于上述困难，在公开发表的文献中少有针对复合材料夹层结构进行可靠性分析的研究工作，目前主要的相关研究工作还是集中在复合材料层合板结构上。Wang等[2]在纤维缠绕圆柱壳的可靠性优化设计中，以缠绕角度为随机变量，在有限元分析的基础上使用Kriging法建立了圆柱壳在压缩载荷作用下线性屈曲响应模型，然后通过模特卡洛模拟得到结构响应的统计特性。Mathew等[3]基于二次可靠度方法结合径向基函数和重要抽样方法开发出一个自适应重要抽样的径向基函数来评估变刚度复合材料层合板失效概率和分析灵敏度，结果表明该方法相比于径向基函数-蒙特卡洛方法节约了95%的计算量。林森[4]基于多项式响应法拟合有限元计算的隐式极限状态方程，通过一次二阶矩法分析了不同压强条件下复合材料压力容器的可靠度。Sun等[5]建议使用自适应更新Kriging模型，并结合蒙特卡洛模拟来处理非线性、小概率和高维度的可靠性问题。周春苹等[6]基于Matlab和NASTRAN的联合仿真技术，构造自适应Kriging模型来代替真实的极限状态函数，使用蒙特卡洛模拟计算出复合材料结构静强度可靠度，并进行了随机变量的失效概率全局灵敏度分析。

目前，代理模型是解决结构分析高计算量的主流方法，常用的代理模型有多项式模型、径向基函数模型、支持向量回归模型、Kriging模型等。结构可靠性分析中应用最为广泛的是多项式模型，但是多项式模型依赖于多项式阶数和项数的选取，并且在高维度和高度非线性问题上精度和效率较低。Kriging模型由于具有理论严谨、逼近精度高以及其与随机方法自然关联的优点，在结构可靠性分析领域得到广泛应用。同时，Kriging模型自身也在不断发展之中，Gaspar等[7]提出了一种主动优化的自适应Kriging代理模型来解决具有非线性和中等规模输入随机变量的结构可靠性问题。Zhang等[8]基于折叠正态分布推导了一种主动学习函数，对自适应截断采样区域进行有效的主动学习迭代。

为了探索复合材料夹层结构多失效模式下的可靠性分析方法，本文以复合材料机身舱段蒙皮夹层结构为研究对象，选取夹层结构的主要力学性能参数和尺寸作为随机变量，根据主要失效模式构造极限状态函数。在此基础上采用Kriging代理模型结合子集模拟方法预测其失效概率。为夹层结构多失效模式的结构可靠性分析和其安全性评估提供方法支持。

1 机身蒙皮夹层结构

本文以单通道中短程客机的机身舱段为分析对象。飞行过程中，民航客机的机身受力形式主要有弯矩、扭矩、剪切力和内部的舱压，同时受到侧面发动机的噪声激励。舱段模型的一端假设为简支边界条件，一端为自由端，组合载荷将施加在自由端上。

1.1 几何尺寸和载荷工况

机身舱段外径R=2 m，长度L=1 m。载荷工况中,弯矩：Mx=900 kNm,My=-2 600 kNm,Mz=-900 kNm；剪力：Qy=-480 kN,Qz=-90 kN;同时受到来自侧边的发动机的噪音激励，频率为200 Hz(参考文献[9]中涡轮螺旋桨发动机的典型频率)，如图1所示。

图1 机身舱段示意图

夹层结构的面板是由T700GC/2510预浸带铺制的层压板，芯材为Rohacell 200WF，夹层的铺层方向为[90/45/0/core/0/45/90]。材料性能参数如表1～2所示。

表1 复合材料面板T700GC/2510性能参数

表2 泡沫芯材Rohacell 200WF性能参数

1.2 数值分析模型

1.2.1 静力分析有限元模型

首先将机身舱段简化为一个长度为1.1 m，外径为2 m的圆柱筒，圆柱筒的一端使用简支约束条件，一端为自由端。自由端在原模型基础上增加了长度为0.1 m的载荷过渡区，如图2所示。这样处理的原因是：复合材料的连接区域需要单独设计和特殊结构处理，而本文的研究对象是非连接区域(分析区)，根据圣维南原理使用载荷过渡区来代替连接区，过渡区具有与分析区相同的材料属性，但是不会发生破坏，这样能够避免直接在分析区加载带来的应力集中、传力路径失真等情况，从而提高分析区的仿真精度。

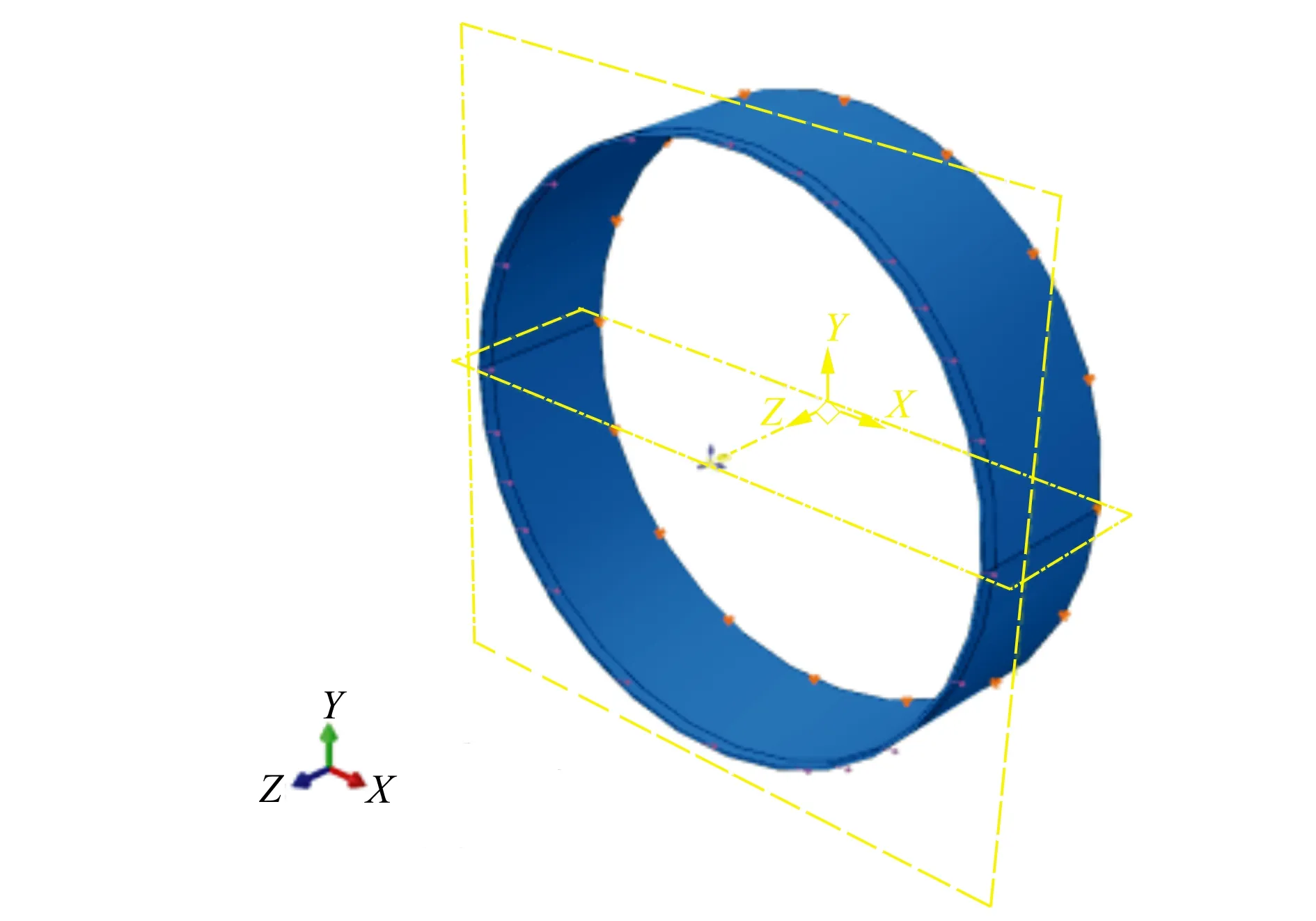
图2 夹层壳体简化模型

本文在有限元软件中建立静力分析模型，内外面板分别使用3层SC8R单元模拟，单元数为3 000。为了模拟出芯材在厚度方向上的应力变化，芯材使用5层C3D8R单元模拟，单元数为5 000。本文旨在研究增强纤维的力学性能和夹层厚度的分散性对结构可靠性的影响，所以未考虑面板分层、面板与芯材脱黏失效模式，这部分失效模式主要受树脂、胶黏剂的性能和制造工艺影响，所以面板与芯材默认有效连接。

面板为碳纤维增强层压板，本文采用Tsai-Wu失效准则[10]逐层分析层压板各层的应力状态，得到各层的破坏指数 。假设面板处于平面应力状态下，Tsai-Wu张量多项式如(1)式所示

式中：IF为破坏指数,IF<1，结构安全；IF≥1，结构破坏

式中：Xt和Xc分别为纤维方向上的拉伸和压缩强度；Yt和Yc分别为面内垂直于纤维方向上的拉伸和压缩强度；S为面内剪切强度。

芯材主要承受面外的剪切和扭转载荷产生的切应力，剪切失效是芯材失效模式中的一种主要失效模式。由于Rohacell 200WF闭孔聚合物泡沫材料具有各向同性[11]，本文采用最大切应力理论进行芯材的静强度评估。单元上的最大切应力τmax可以通过最大、最小主应力计算，芯材单元的最大切应力计算公式

(2)

式中:σ1和σ3分别为最大主应力和最小主应力。

图3和图4给出了在名义均值点处分析区内面板的Tsai-Wu失效指数IF分布图、芯材的Tresca应力分布图(Tresca应力是主应力间的最大差值，是单元上最大切应力的2倍)。图中的变形放大系数为20。

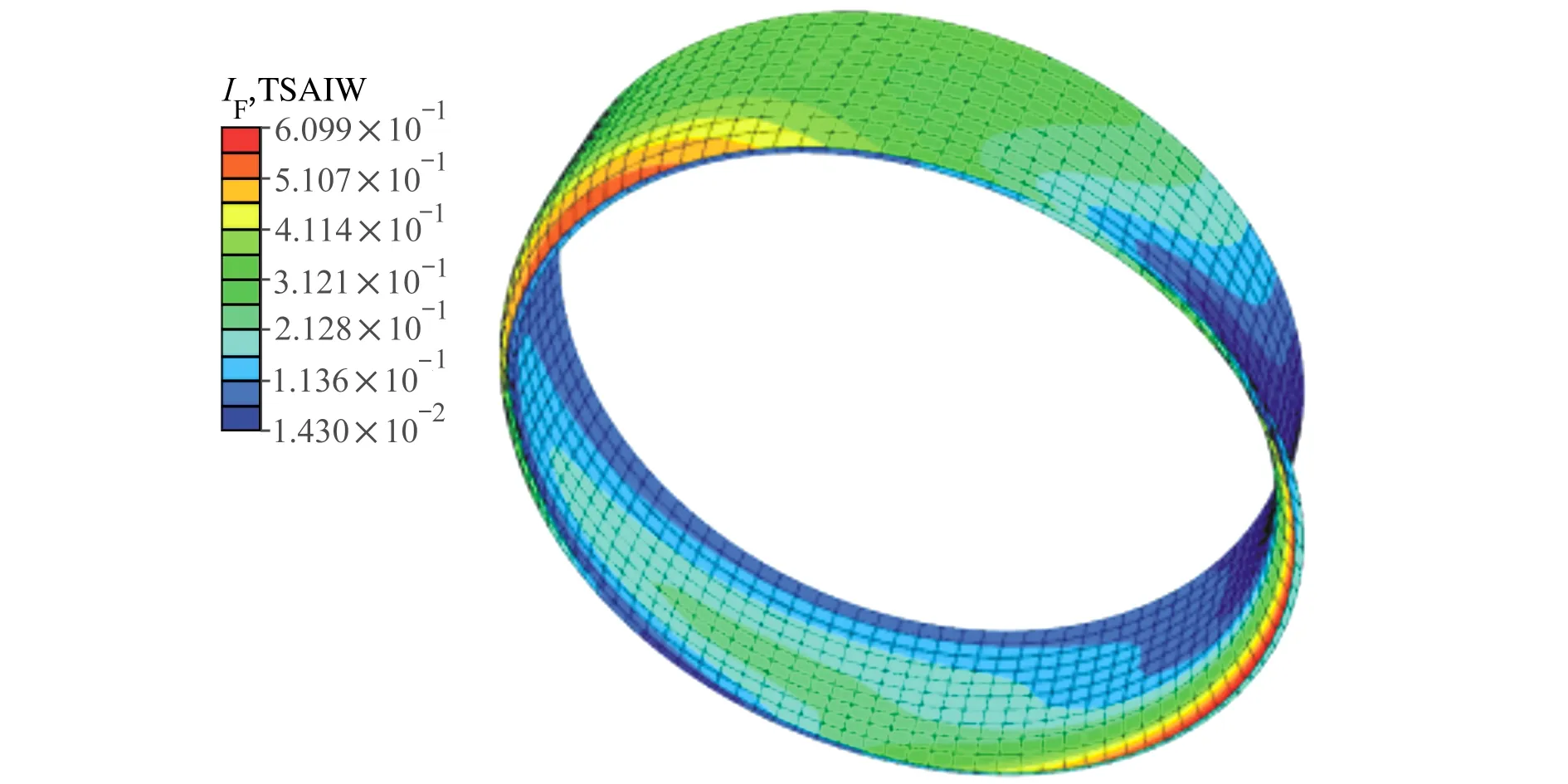
图3 面板Tsai-Wu失效指数IF分布图

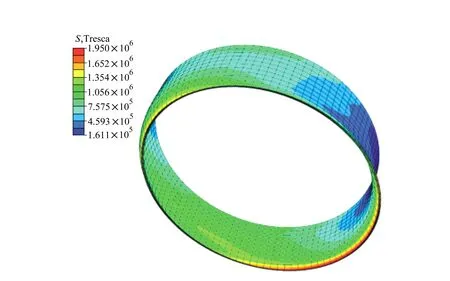
图4 芯材Tresca应力分布图

1.2.2 线性屈曲分析模型

在Abaqus中建立线性屈曲分析模型，采用摄动分析方法和子空间迭代法提取前10阶模态。因为本文所建立的数值模型中含有coupling约束，故无法使用Lanczos法，并且在少量(少于20)的模态提取时，子空间迭代方法一般更快。夹层壳体的一阶屈曲模态如图5所示。

图5 夹层壳体的一阶屈曲模态

1.3 声学边界元模型

由于声学分析涉及到动力学响应计算，且计算过程相对静力学分析要复杂得多。本文在进行蒙皮夹层结构声学分析前，先在商业有限元软件中建立了壳体的谐响应分析模型，求解得到壳体表面法向振动速度，然后进行声学响应分析。

谐响应分析是计算在双侧200 Hz的单位激振力作用下夹层壳体表面的法向振动速度，夹层厚度方向上的应力变化对结果影响很小，所以为了提高效率，面板和芯材都使用壳单元来模拟。整个模型单元数为2 000，结构阻尼系数设置为0.02。谐响应分析需要考虑结构中预应力的影响，飞行载荷会对机身蒙皮夹层结构作用产生预应力，在动力学工况中需要将静载荷引起的刚度影响结果引入到动力学分析中。壳体表面的法向振动速度如图6所示。

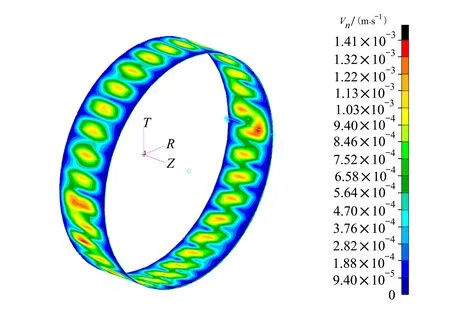
图6 声学模型表面振动速度分布图

声学边界元模型如图7所示，计算结果中结构网格上的法向振动速度被映射到黄色区域的声学边界元网格上，边界元网格内部的3个红色网格模拟舱内一侧的人耳，即场点位置，声学分析的目的就是计算6个场点位置(选在客舱内乘客头部位置)的声压级，从而对发动机噪声激励下舱内声压水平进行评估。

图7 声学边界元模型

2 蒙皮夹层结构可靠性模型

2.1 随机变量

由于面板主要承受面内的应力，与面板垂直的2个力学常数G23和G13对分析结果影响相对较小，故不作为随机变量考虑。本文选取的随机变量有面板的力学性能参数E11,E12,v12和G12，芯材的力学性能参数Gc，以及夹层的各层厚度ft1,ft2,ft3,ct,ft4,ff5和ft6，共计12个随机变量。面板材料的统计特性数据来自复合材料手册[12]，汇总在表3中。

表3 随机变量的统计特性

2.2 极限状态函数

夹层壳体的面板主要承受弯曲引起的正应力；内层的芯材主要用于承受剪力、保持面板的形状和结构的稳定性。机身蒙皮夹层承受的载荷主要有弯矩、扭矩和剪切力以及座舱压力，复杂的载荷情况使得机身夹层的失效模式较为复杂，泡沫夹层的主要失效模式包括面板失效、芯材剪切失效、面芯脱胶、面板皱曲、整体屈曲、剪切皱折等[13]。为了研究复合材料的主要力学性能和夹层厚度尺寸的分散性对结构的影响，本文主要考虑与这些不确定因素直接关联的3种主要失效模式:面板失效、芯材剪切失效和整体屈曲。同时从功能性角度出发考虑到现代民航客机机身对降低舱内振动噪声的要求，本文把在发动机的噪声激励下引起的舱内振动噪声超标作为一个主要失效模式予以分析。同时受限于作者的学科和已掌握的结构仿真分析方法，本文选取了3种典型失效模式，旨在说明所提设计框架在解决多功能一体化设计带来的多源、多失效模式问题时的可行性和优势，而实际中机身结构设计应不只考虑这3种失效模式。下面根据蒙皮夹层结构的设计要求给出3类典型的极限状态判据。

2.2.1 面板、芯材的静强度失效

本文复合材料面板的静强度评估使用Tsai-Wu失效准则实现，芯材静强度评估使用最大切应力理论实现。有限元法将夹层圆筒分割成n个单元，任一个单元失效，都会导致整体失效。计算得到面板单元上Tsai-Wu失效指数的最大值IF和芯材单元上的最大切应力值τm，根据面板静强度失效和芯材剪切失效分别给出以下失效判据：

式中，i为单元的编号，i=1,2,…,n。

2.2.2 整体屈曲失效

机身作为重要的主承力结构，须在组合载荷下保证其稳定性，并且机身结构的刚性要求较大。因此本文将整体屈曲失效作为主要失效模式之一加以考虑。线性屈曲理论是基于小挠度、线弹性的假设，在不考虑结构受载后的变形和初始缺陷的情况下对结构进行稳定性分析。

在有限元软件中的特征值屈曲预测分析中有

(K0+λiΔK)vi=0

(4)

式中：K0为基础状态的刚度矩阵；ΔK为递增载荷曲线Q的微分初始应力刚度矩阵；vi为屈曲模态的位移特征向量；λi为第i个特征值。

临界载荷

pcr=p0+λiQ

(5)

一般来说，先达到第一阶特征值处的屈曲载荷率从而引起屈曲失稳。在给定分析载荷情况下，为防止失稳，线性屈曲特征值λ需要满足：|λ|>1。

2.2.3 振动噪声超标

发动机作为舱内噪声的主要来源，民机飞行过程中，机身侧面受到来自发动机的噪声激励，引起机身壁板的振动，振动的壁板进一步激励舱内空气产生内部噪声。由于载荷和位置的不对称性，本文计算了6位乘客的耳朵位置场点的声压级，噪声超标判据为

max{P1,…,Pj,…}>60 dB

(6)

式中：Pj为第j个场点位置的声压级。基于此，建立振动噪声极限状态函数。

2.2.4 蒙皮夹层结构系统极限状态函数

蒙皮夹层结构的极限状态由多种失效模式确定，任意一种失效模式出现都会导致夹层结构整体失效，因此将蒙皮夹层结构作为一个串联结构系统加以分析，其可靠性框图如图8所示。

图8 机身可靠性框图

最终蒙皮夹层结构系统的极限状态函数为

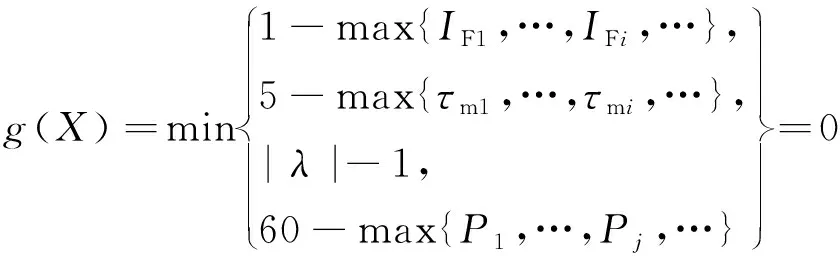
(7)

g(X)<0表示夹层结构在上述3类失效模式下失效。

3 参数化建模和程序化前后处理

为了克服计算量过大的问题，本文使用子集模拟方法预测夹层机身的可靠度。随机抽样方法的一个重要特点就是需要进行大量的抽样分析计算。尽管使用子集模拟方法和Kriging代理模型来提高抽样效率，但是多种失效模式下需要计算多个极限状态函数，每个极限状态函数的代理模型需要一定的样本点来保证逼近的精度，所以重复而大量的数值分析计算必不可少，这就需要参数化建模和程序化地协同控制各个分析软件完成各自的模型修改、计算、结果提取和处理工作。

编写统一控制各分析软件的控制代码，并封装成函数方法，以随机变量向量为输入，输出各个响应的数值分析结果向量Y。控制分析流程如图9所示。

图9 仿真分析流程图

4 蒙皮夹层结构可靠性分析

为了将蒙皮夹层结构可靠性分析的计算量降低至工程设计可接受的范围，本文采用Kriging代理模型逼近原始数值计算模型，同时为了进一步降低计算量，采用子集模拟方法计算失效概率。

4.1 抽取训练样本

对于耗时的数值仿真试验，需要考虑在保证近似精度的同时，研究如何使用少量的样本点来进行试验设计。鉴于拉丁超立方抽样的样本分层、分布均匀等优点，本文采用拉丁超立方抽样产生构建Kriging模型所需的初始样本点。

由于拉丁超立方抽样是在标准化空间[0,1]内抽样，因此在结构可靠性分析中，随机变量的样本值一般通过逆变化的方法获得。例如在第i维上，拉丁超立方抽样抽取的样本值为ui，那么对应的随机变量值xi为

(8)

式中，Fi为输入随机变量Xi的累积概率分布函数。

4.2 构造Kriging代理模型

在获取初始样本点后，本文利用Dace工具箱[14]为蒙皮夹层结构的3种失效模式和系统失效建立Kriging代理模型。代理模型构造流程图如图10所示。

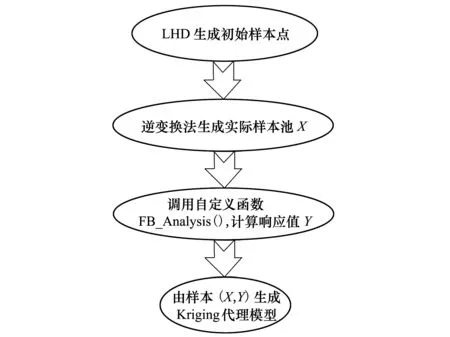
图10 Kriging模型构造流程图

4.3 代理模型误差检验

由于民机结构的失效风险在10-9左右，服从正态分布的随机变量落在[μ-6.5σ,μ+6.5σ]区间外的风险为8.03×10-11，区间外的部分对结果精度的影响小于8%，所以只需要保证代理模型在该区间内的精度。本文使用拉丁超立方抽样方法在随机变量的区间[μ-6.5σ,μ+6.5σ]内按均匀分布抽取100个检验样本点。分别用有限元/边界元数值计算模型和Kriging模型计算检验样本的响应值、预测值以及相对误差。每个检验样本有4个响应，分别对应面板Tsai-Wu失效指数IF、芯材最大切应力τm、整体线性屈曲特征值λ及场点的最大声压级Pmax。检验样本的响应值按照升序排列，对应的Kriging模型预测值、相对误差如图11～14所示。Kriging模型的最大预测误差小于3.5%，并且95%的检验点的相对误差在1.5%以下，预测效果理想，可进一步用于结构可靠性分析。

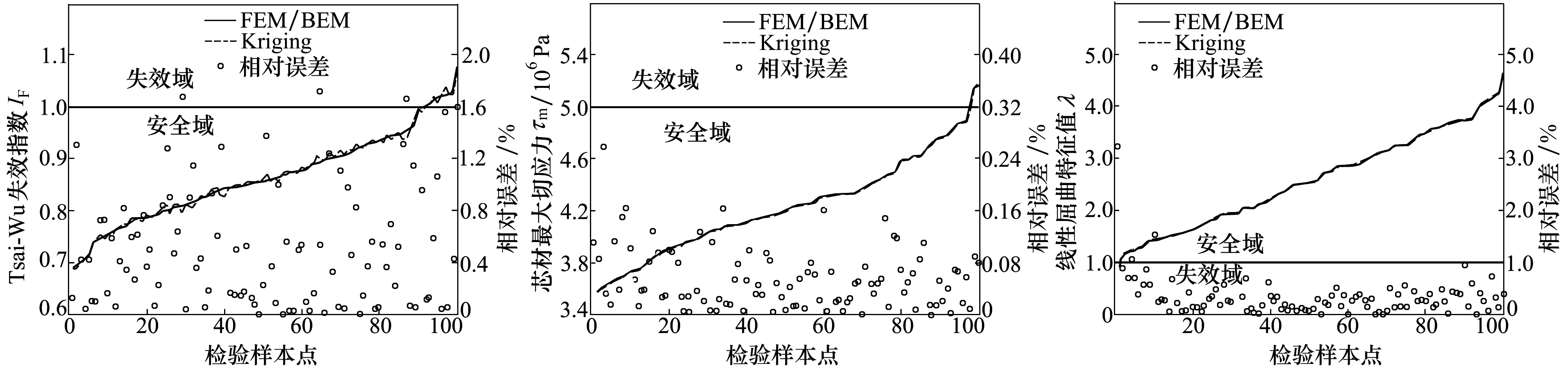
图11 面板Tsai-Wu失效指数IF对比图 图12 芯材最大切应力τm对比图图13 线性屈曲特征值对比图

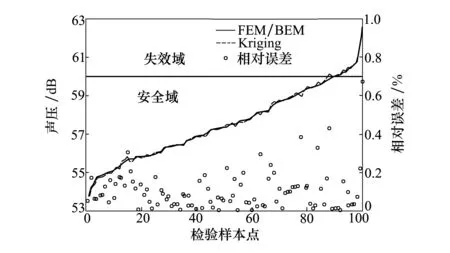
图14 内场声压级对比图

4.4 失效概率评估

完成代理模型构建后，本文采用子集模拟方法计算3个失效模式和蒙皮夹层结构系统的失效概率。子集模拟方法是一种先进蒙特卡洛模拟，继承了蒙特卡洛方法能够解决高纬度、非线性问题的优点，同时提升了求解小失效概率问题的能力。其基本原理是运用小概率事件可以由一系列较大条件概率的乘积来表示，将小失效概率事件模拟转化为较大条件失效概率事件来模拟，其关键步骤为产生服从条件分布的新样本[15]。

本文中子集模拟方法参数设置如下：每层样本数N=1 000，中间事件的条件概率P0=0.2。考虑到民机最大失效风险为10-9，子集模拟的最大迭代层数设为15，可以覆盖该小失效概率范围。经过10轮重复计算，前述3类失效模式和蒙皮结构系统的失效概率如表4所示。同时表中给出了失效概率计算结果的标准差和变异系数，可以看出10次失效率计算结果都在均值附近，最大的变异系数为1.479 7，说明所提方法具有较高的稳定性。本文1次系统失效概率的分析计算中大约需要9 800次结构系统响应分析，Kriging代理模型方法节约计算时间为9 800(tnum-tkri),tnum,tkri分别为数值分析和Kriging方法用时，分析模型越复杂，数值分析耗时越长，而Kriging模型方法分析用时基本不变，该方法效率越显著。3个分失效模式中噪声超标的失效率最大，应予以关注，结构系统的失效率与该主失效模型的失效率在同一量级。

表4 失效概率计算结果

5 结 论

本文提出了一种结构可靠性分析框架，用于复合材料夹层结构的可靠性分析。以民机机身蒙皮结构为例，利用多种有限元软件对夹层壳体进行参数化建模分析和自动程序化前后处理，得到不同参数组合下的数值分析结果。基于试验设计技术和数值分析结果构建各个极限状态函数的Kriging代理模型，并结合子集模拟方法分析了结构在各个单一失效模式下的失效概率和多失效模式下结构系统的失效概率。分析计算结果，可以得出如下结论：

1) 参数化建模和自动程序化前后处理是多维度、多失效模式分析的必要技术方法，多失效模式涉及不同的仿真分析软件，不同分析软件之间协同控制是解决问题的关键之一；

2) 使用同一组初始样本点，构建的Kriging模型能够对夹层结构的极限状态函数进行高效的全局近似，最大相对误差达到2.4%以下；结合子集模拟方法求得各单一失效模式下和整体的失效概率的变异系数最大为1.479 7，表明了所提方法的高效性和稳定性；

3) 本文方法的适用性取决于3个部分：结构仿真分析、Kriging代理模型及可靠性分析方法。结构仿真分析目前已在力学、声学、热学等学科中广泛应用，建立相应的参数化模型以及可靠性分析程序与仿真分析输入、输出的联系是使用本文方法的前提，所以该方法的适应性主要受限于结构分析的计算量；Kriging代理模型结合子集模拟可靠性分析方法克服了结构响应函数的非线性、隐式化问题，特别是机身结构在中、高频段的外部激励下的结构响应呈现高度非线性的特点，这能在很大程度上验证所提方法的适应能力;

4) 夹层结构整体可靠度主要取决于失效概率最大的失效模式，本文中蒙皮夹层的噪声水平超标对应的失效概率最大；为了提高蒙皮夹层结构系统的可靠度，应首先考虑减少该失效模式的失效概率，对影响噪声水平的设计变量进行优化。

本文所提方法适用于结构分析与设计阶段对机身蒙皮夹层结构的可靠性进行量化分析，为其他夹层结构的多失效模式下的可靠性提供了一定的方法参考。