串联机器人运动学建模与轨迹规划研究

于 昊,陈 桂,丁 飞,许艺严

(南京工程学院自动化学院, 江苏 南京 211167)

“中国制造2025”提出以来,以串联机器人为代表的机电一体化智能制造产品呈现爆发式的增长,在工业生产和制造等领域起到了显著的作用[1].串联机器人模仿人的手臂结构,可以灵活地代替人力完成重复度高、危险性大的工作任务,而轨迹规划作为机器人运动学的重要组成部分,一直以来是研究的重点.合理的轨迹规划,可以提升机器人的工作效率和运动性能[2],延长机器人的使用寿命.

本文以IRS300-3机器人为例,采用Denavit-Hartenberg(D-H)建模方法[3],借助Matlab Robotics机器人工具箱,对六自由度串联机器人进行建模与运动学分析;采用五次多项式插值方法,基于pick-and-place operation(PPO)路径规划码垛轨迹,分别实现机器人在关节空间与笛卡尔空间的轨迹规划,对比两种轨迹规划后的机器人的运动曲线,将规划出的轨迹在基于CODESYS的机器人控制平台上运用至IRS300-3机器人本体[4],有效提高了串联机器人的码垛工作效率.

1 机器人运动学建模

IRS300-3机器人是一款六自由度串联机器人,其机械结构图如图1所示.本例机器人有6个关节轴,对每个关节轴进行分析,建立连杆坐标系.在第i(i=1,2,…,6)个连杆坐标系中,zi轴沿关节轴i的指向,xi轴沿公垂线的指向,如果关节轴i和关节轴i+1相交,则xi轴垂直于关节轴i和关节轴i+1所在平面,yi轴根据右手法则确定.

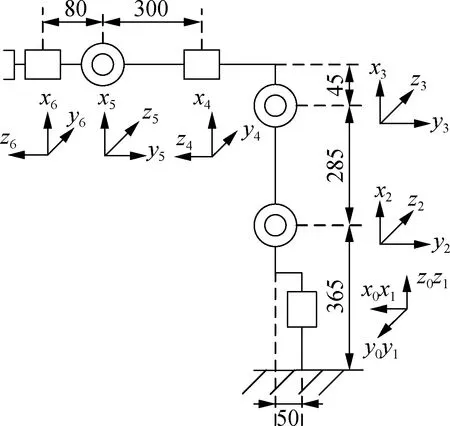
图1 IRS300-3机器人机械结构图(mm)

D-H模型是以连杆参数来表述机构运动关系的运动模型,依据D-H参数法得到的IRS300-3机器人D-H参数如表1所示.

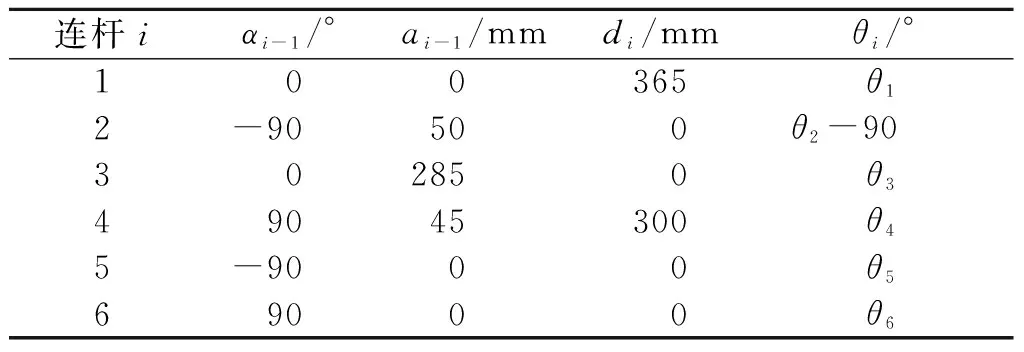
表1 IRS300-3机器人D-H参数

利用Matlab Robotic机器人工具箱的Link函数和SerialLink函数,以表1参数建立如图2所示的IRS300-3机器人的运动学模型.

图2 IRS300-3机器人运动学仿真模型

2 运动学分析

为了得到描述机器人末端执行器在笛卡尔空间的位姿矩阵,需要建立坐标系i相对于坐标系i-1的变换,然后将这些独立的变换串联起来,得到坐标系6相对于坐标系0的位置和姿态.

坐标系i在坐标系i-1中的描述可以看成坐标系i沿zi轴平移di,并绕zi轴旋转θi,之后沿xi轴平移ai-1,并绕xi轴旋转αi-1,得到的齐次变换矩阵为:

(1)

将表1中的D-H参数带入式(1),可得到机器人相邻两个关节坐标系之间的变换关系,则机器人末端执行器所在坐标系6相对于基坐标系0的位姿变换矩阵可表示为:

(2)

式中:(r11r21r31)T、(r12r22r32)T、(r13r23r33)T为机器人末端执行器相对于基坐标系的姿态向量;(pxpypz)T为机器人末端执行器相对于基坐标系的位置向量,分别代表空间中的x、y、z轴坐标.

基于蒙特卡洛法对机器人进行工作空间分析,在D-H参数已知的情况下,根据式(2)可以得到机器人末端执行器的位置与姿态关于θi(i= 1,2,…,6)的函数:

(3)

根据IRS300-3机器人各个关节的运动限位,利用rand函数生成6个关节的随机变化量,带入式(3)得到机器人末端执行器在三维空间中的位置:

θi=θimin+(θimax-θimin)rand

(4)

式中,rand为[0,1]的随机数.

随机取样次数N越大,得到的机器人工作空间越准确[5].在Matlab环境中,选取随机次数为100 000,得到机器人工作空间云图如图3所示.由图3可见,该机器人的末端执行器可以抵达臂长范围内三维空间的任何一个位置.

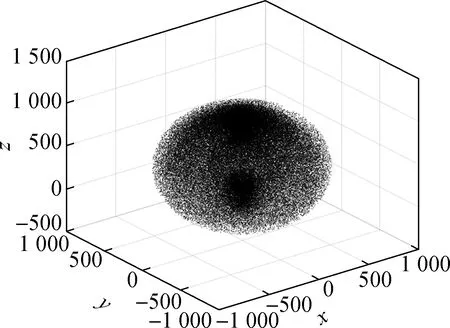
图3 工作空间

3 机器人轨迹规划仿真及分析

轨迹是指机器人在运动过程中走过的路径、各路径点的速度和加速度在时间上的变化,而轨迹规划是根据作业任务的要求计算出预期的运动轨迹[6].轨迹规划的基本问题是将机器人末端执行器从初始位置移动到目标位置,在这个过程中使其位置、速度、加速度关于时间的曲线尽可能地平滑,从而保证整个机器人运动过程的平稳.

根据目标所处空间的不同,可以分为关节空间规划方法和笛卡尔空间规划方法[7].关节空间轨迹规划不需要考虑路径点之间的轨迹形状,仅以关节角度的时间函数来描述机器人的轨迹,适用于码垛、分拣等应用场景;笛卡尔空间轨迹规划是将机器人末端的位移、速度、加速度以及加加速度表示成时间的函数,适用于焊接、喷漆等应用场景.

3.1 多项式轨迹规划

为保证机器人运动的平滑性,要定义一个连续的、具有一阶导数的平滑函数,让机器人的运动轨迹与其相拟合[8].为保证机器人在运动过程中加速度曲线平滑、避免震荡,需要这个函数三阶连续可导.这就需要用五次及以上多项式曲线进行轨迹规划.如果对作业曲线有更高的要求,则需要用更高阶的多项式曲线与轨迹拟合.

本文主要讨论五次多项式函数插值的方法,这种方法原理简单,不仅适用于串联机器人,在其他工业机器人轨迹规划场合也有广泛的应用[9].

假设机器人的第i个关节在时间段[t0,tf]内五次多项式插值的关节位置函数为:

θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(5)

式中，a0、a1、a2、a3、a4、a5为待求未知量.

对式(5)分别求其一阶导数和二阶导数,可以得到关节速度和加速度的函数:

(6)

6个未知量需要6个约束条件求解,令:

(7)

将式(7)的6个约束条件代入式(5)和式(6),解得五次多项式系数为:

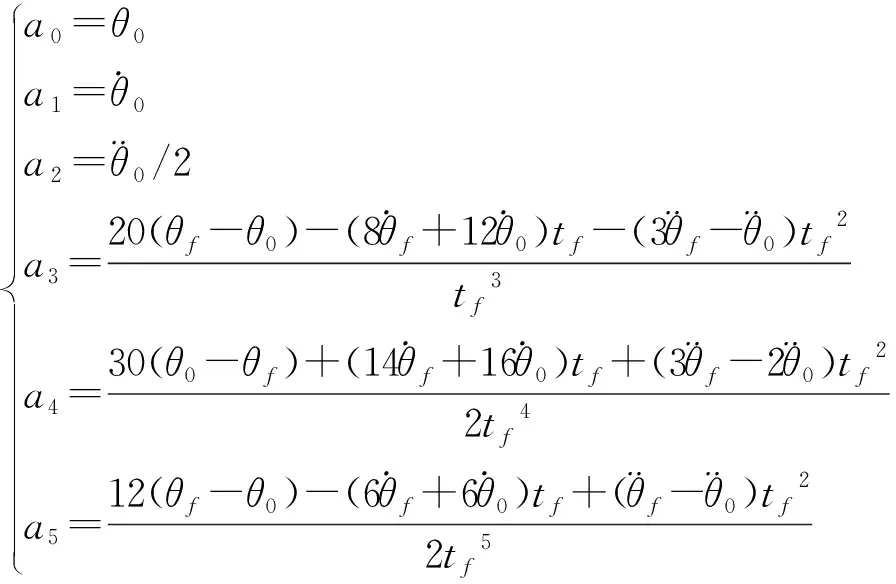
(9)

3.2 PPO轨迹规划目标分析

串联机器人根据作业的需要在不同的应用场景扮演着不同的角色.在高速流水线上进行码垛、分拣、搬运和筛选等高重复度机械作业时,主要的动作为抓取(pick)与放置(place).在这些机器人应用场景中的轨迹被统称为PPO轨迹[10-11].

如图4所示,串联机器人的PPO路径呈门字型,设定轨迹的关键点分别为初始点P1、平移点P2、平移点P3和放置点P4.通常会给定初始点和放置点的位置、机器人抓取高度、放置高度以及运行距离,要求串联机器人在初始点P1抓取物料,经PPO轨迹途经平移点P2和平移点P3,将物料放于放置点P4,最后又沿PPO路径返回初始点P1,完成一次抓取与放置的循环.

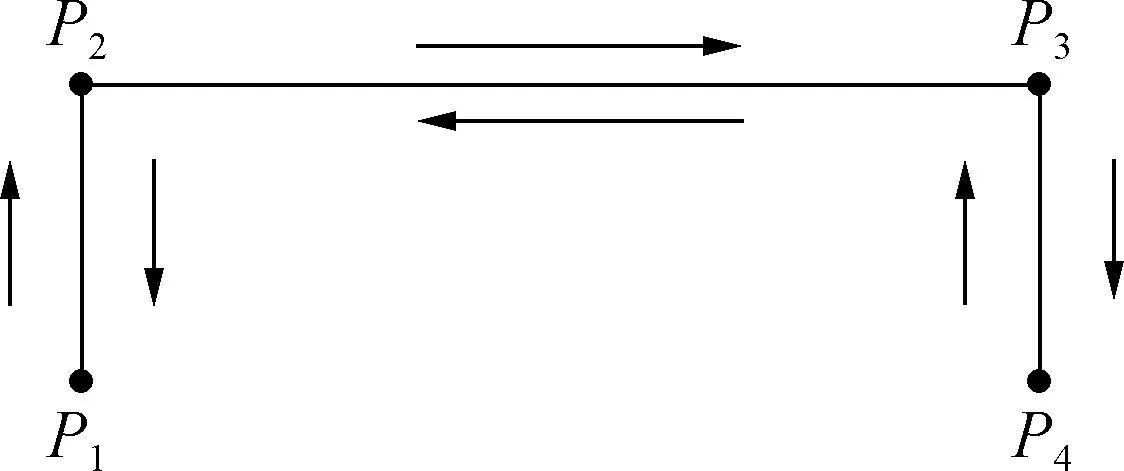
图4 PPO轨迹示意图

3.3 轨迹规划仿真

在Matlab环境中,基于建立的运动学模型,依据作业要求及五次多项式插值的轨迹规划方法进行PPO轨迹规划的动态仿真.

设在时间段[0,1]内,取插值初始点P1(-421.5,0,305.2)、放置点P4(-210.7,365,305.2),机器人抓取和放置高度为P1P2=P3P4=100 mm.

串联机器人末端执行器分别在关节空间和笛卡尔空间下进行轨迹规划,得到的轨迹对比图如图5所示.

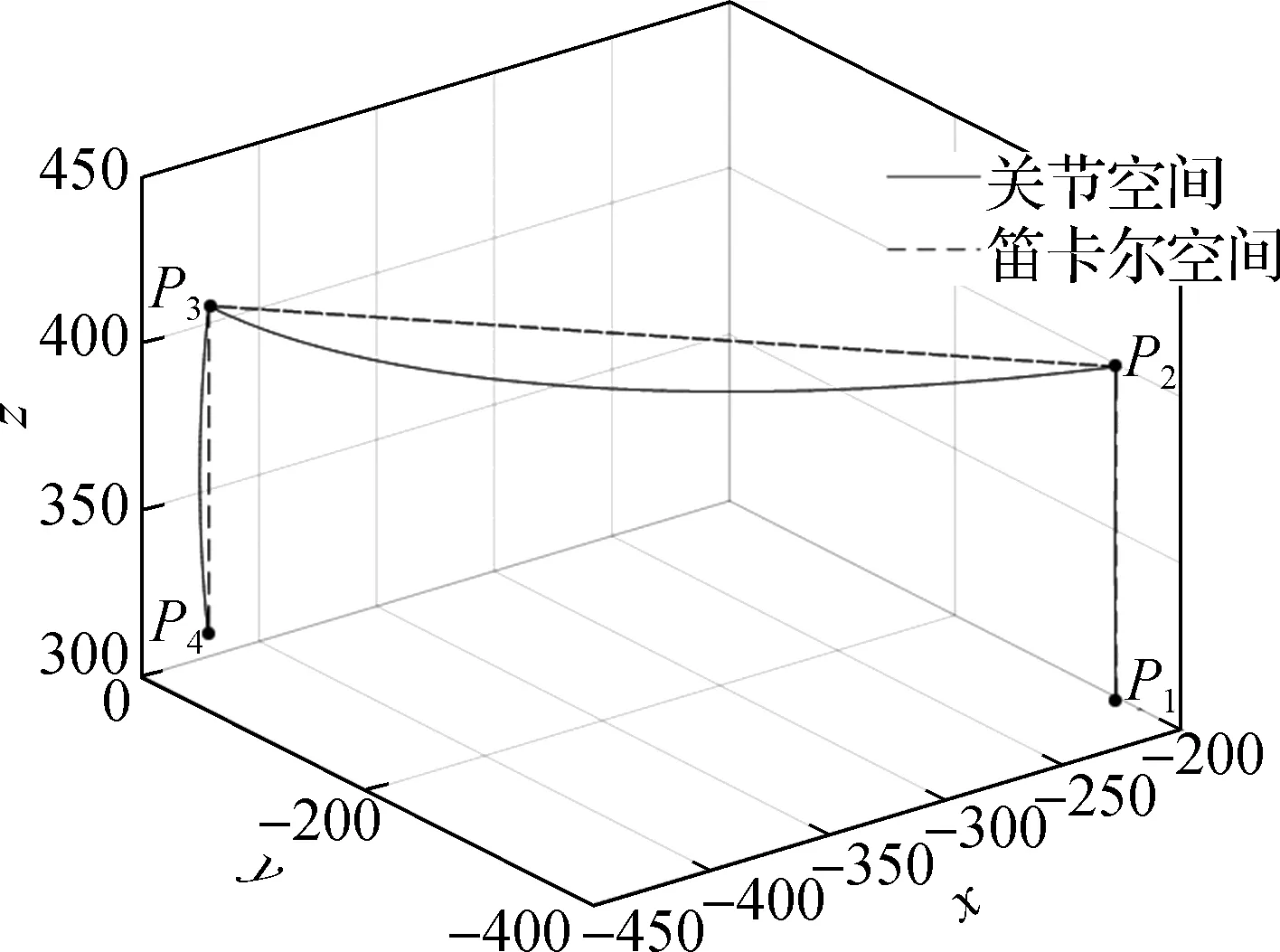
图5 末端执行器两种轨迹对比

由图5可见关节空间的轨迹呈圆弧形状、笛卡尔空间的轨迹呈直线形状,两条轨迹均途经点P1、P2、P3、P4,符合PPO路径的基本要求.

选取关节2、关节3观察其关节角的变化,图6为在相同插值方法的条件下,串联机器人关节2、关节3的角度处于关节空间轨迹规划和笛卡尔空间轨迹规划的变化情况对比.

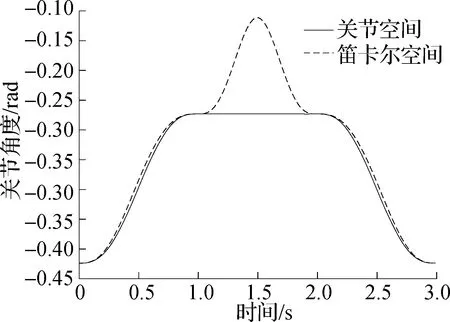
(a) 关节2

由图6可见,笛卡尔空间轨迹规划中1、2 s处存在关节角度的突变,这两处时间点分别是PPO路径上的拐点P2、P3.造成关节角度突变的原因为:关节空间轨迹规划时,直接对起止位置的角度进行多项式插值计算,每个关节角之间的变化相对独立,前一个关节角度的变化不会影响到后一个关节角;笛卡尔空间轨迹规划时先对机器人末端执行器的位姿进行多项式插值计算,然后将得到的位姿插值点逆运算求解出关节角度;由于笛卡尔空间和关节空间存在着非线性映射关系,当这些插补点经过运动学逆解映射到关节空间时,6个关节之间相互影响,形成如多骨诺米牌一样的连锁效应.

4 实物调试验证

在IRS300-3机器人上对设计的PPO路径五次多项式插值算法进行在线测试.输入初始点P1和放置点P4的坐标以及机器人抓取和放置高度,经插值算法计算出插值点,控制机器人6个关节轴的伺服电机在位置模式下进行插补运动,得到各个关节角度、角速度、角加速度变化曲线如图7所示.

(a) 角度

由图7可见,采用五次多项式插值的轨迹规划方法,关节角度、角速度、角加速度均无明显突变,机器人运动平稳且振动小.

选取关节1,观察其关节角度变化,对比在Matlab环境中仿真规划的关节角度轨迹,得到机器人的跟踪性能曲线如图8所示.由图8可见,机器人的跟踪轨迹存在0.3 s的延迟,形状与规划轨迹一致,能够完成轨迹规划的任务.

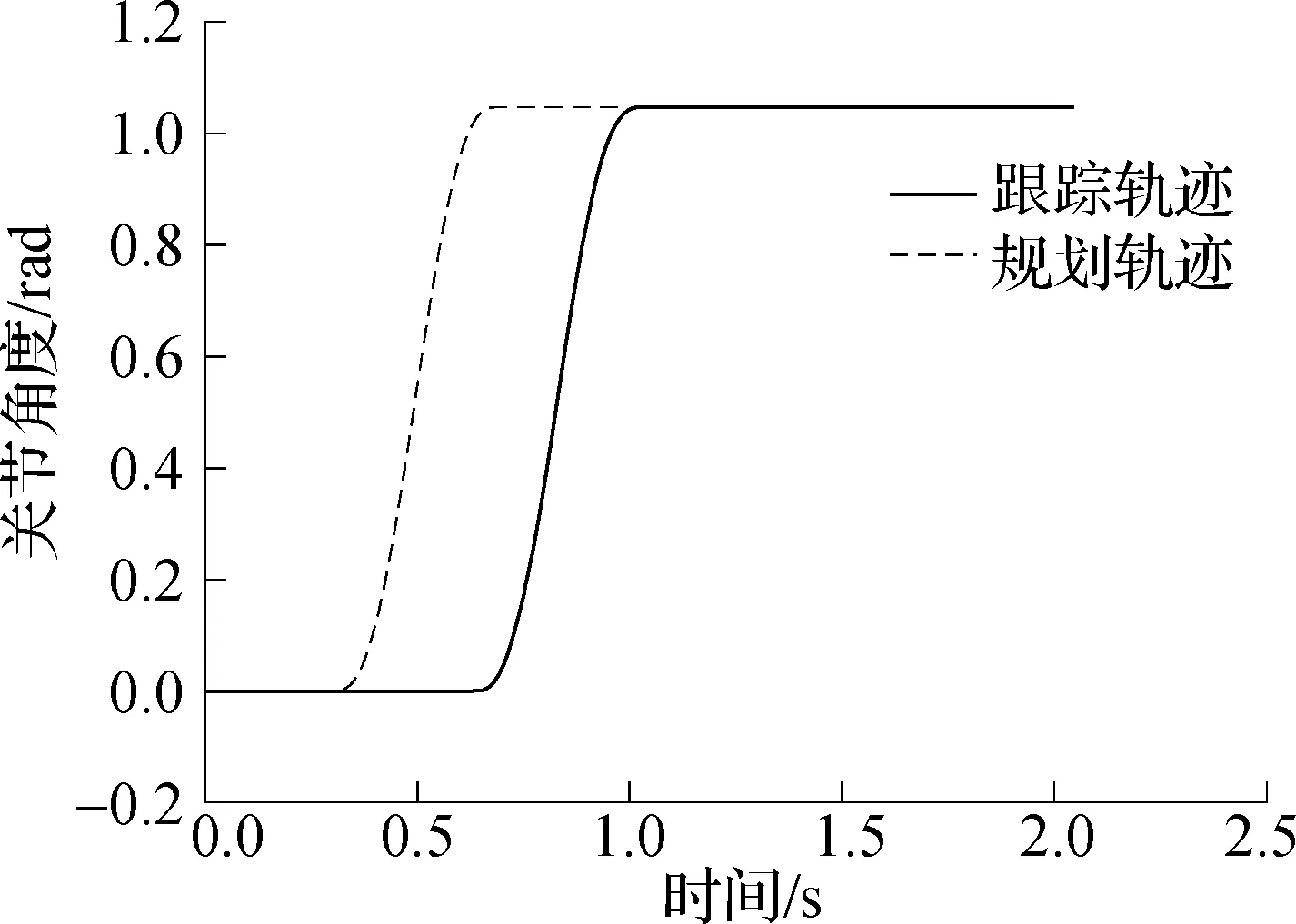
图8 单关节角度跟踪性能曲线

5 结语

基于PPO路径规划码垛任务轨迹,应用Matlab Robotics机器人工具箱建立机器人运动学模型,分别实现了机器人在关节空间和笛卡尔空间下的五次多项式插值的轨迹规划仿真与对比.仿真结果显示,关节空间的轨迹呈圆弧状,适用于空间开阔、无障碍物的工作场合,笛卡尔空间的轨迹呈直线状,机器人末端执行器的精度高,便于控制,适用于喷涂、焊接的工作场合.

将规划的轨迹在基于CODESYS的硬件平台上运用至IRS300-3机器人本体进行试验,结果验证了模型的正确性,表明使用五次多项式插值轨迹规划方法后,得到的运动曲线平稳,关节角度、角速度、角加速度无剧烈变化,轨迹的跟踪性能良好.