基于改进ECC和AES算法的边缘数据保护技术研究*

房照东 李永忠

（江苏科技大学计算机学院 镇江 212003）

1 引言

数据安全是构建工业互联网安全系统的关键。针对边缘数据中的指令数据，由于边缘数据安全要求较高，通常采用数字签名技术保证数据的完整性和来源。文献［1］提出了采用双私钥、双基点的方式改进数字签名算法，提高了数字签名中私钥的安全性，但是仍采用模逆操作，签名和验签速度较慢。文献［2］针对去除模逆操作在安全性上的不足，提出了使用随机数和私钥结合的方式生成数字签名，同时去除模逆操作，但是该方式并未考虑到私钥的安全性问题。

本文针对以上问题，在数字签名过程中采用双私钥和双基点以保证私钥的安全性，加入一个随机数以提高数字签名的安全性，去除模逆操作以提高数字签名速率。使用改进ECC和AES混合加密算法对边缘数据进行加解密操作。实现边缘数据的安全存储和传输。

2 算法概述

2.1 AES算法

AES（Advanced Encryption Standard，高级数据加密标准）算法［3］是美国联邦政府采用的一种区块加密标准，旨在取代DES（Data Encryption Standard）算法，成为新一代加密标准。该算法安全、快速、易于实现且能在各个平台上实现。AES算法是一种对称密钥的分组迭代加密算法，分组长度固定为128bit，密钥长度分为128bit、192bit和256bit三种不同的长度，密钥长度不同，加密轮数也不同。

2.2 ECC算法

ECC（Elliptic Curve Cryption System，椭圆曲线密码）算法［4］是利用椭圆曲线来实现的密码技术的统称。160bit长度的椭圆曲线算法密钥与1024位的RSA密码技术安全性相同，且具有在私钥加解密速度上比RSA［5］、DSA［6］等速度更快，存储空间更小，带宽要求更低等优点。

将椭圆曲线定义在有限域上，使之变成离散的点，即转化为椭圆曲线离散对数问题［7］。这个性质是椭圆曲线密码体制的基础，可根据这个性质实现公钥密码、数字签名和密钥交换。

在使用ECC算法进行数字签名过程中，私钥并非绝对安全，由于ECC的公钥是公开传输的，某些攻击手段可以根据公钥推算出私钥。其次ECC加解密过程中的模逆操作会降低算法加解密速度。

2.3 哈希函数

安全哈希算法（SHA-1）［8］是MD4算法家族中使用最广泛的信息摘要函数。该算法基于Merkle-Damgard结构［9］。在压缩函数过程中，最大消息长度为264位，输出长度160位，计算过程中将消息分成512位的分组进行处理。压缩函数总共有80轮，而这80轮又分成每组20轮的不同阶段。最终得到160位消息摘要。

3 改进ECC和AES混合加解密算法的设计

3.1 对ECC数字签名算法的改进

本文提出了一种采用双私钥和双基点，在签名和验签过程中加入一个随机数并去除模逆操作的改进方案。具体改进过程如下：

1）改进的数字签名过程

改进的数字签名过程如图1所示。

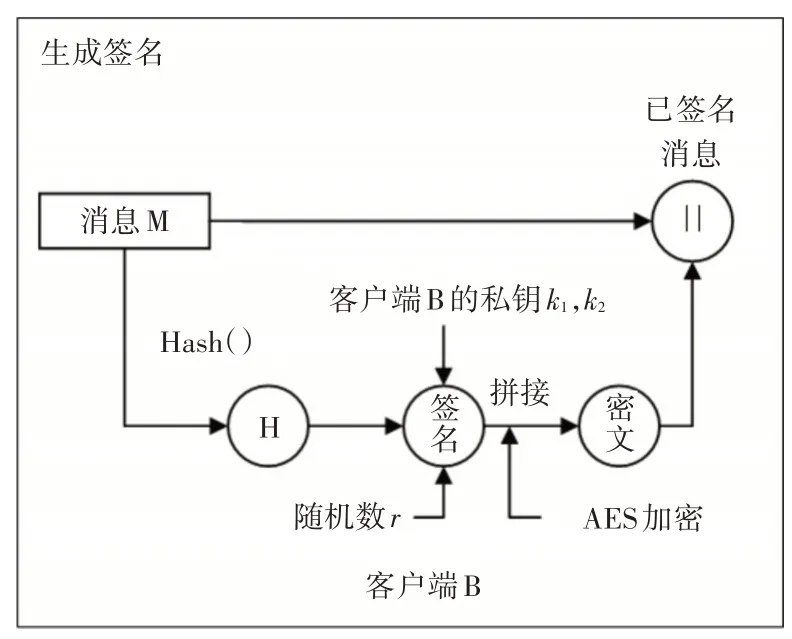
图1 生成数字签名过程

具体实现过程如下：

step1：选择一个随机数或伪随机数r，r∈[1，n-1]；

step2：基于基点G1、G2计算

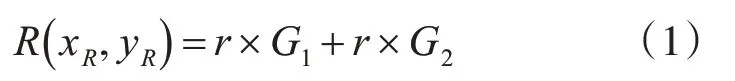
step3：计算x≡xR(modn)，其中xR为R的横坐标（如果x=0，则转步骤（1））；

step4：对需要签名的消息M通过散列函数计算其散列值，H=Hash(M，x)，将H转换成整数；

step5：生成签名：

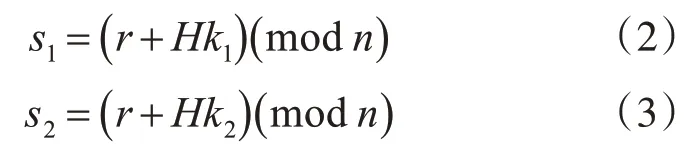
（若s1=0或s2=0，则转步骤（1））；

step6：客户端B将x，s1，s2和M拼接，使用AES加密生成密文c发送给服务器A。

2）改进的验证签名过程

改进的验证签名过程如图2所示。

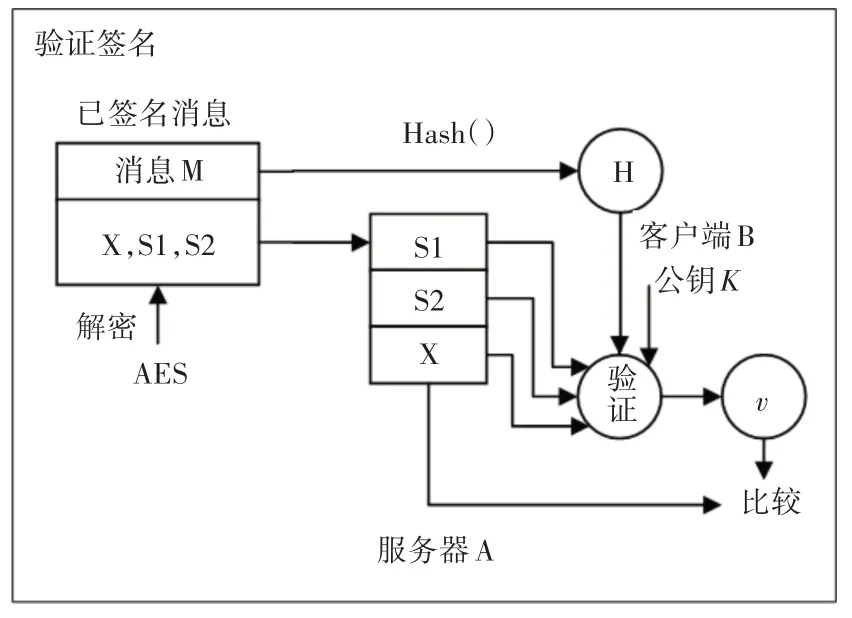
图2 验证数字签名过程

具体实现过程如下：

step1：服务器A接收到密文消息c，使用对称密钥解密，得到x，s1，s2和消息M；

step2：判断x，s1，s2是否属于[1，n-1]，否则签名无效；

step3：服务器A使用客户端B相同的散列算法H=Hash(M，x)；

step4：计算

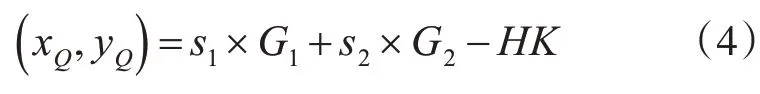
若Q=0，则签名无效；

step5：计算

step6：比较v和x，若相等，则验证成果，否则签名无效。

3.2 AES算法设计

在AES算法实现中，首先将明文分组得到数据块，数据块经过多层转换操作，每次转换产生一个中间结果，称为状态（State）［10］。加解密过程在4×4的字节矩阵上重复执行字节替代、行变换、列混合和轮密钥加四个不同的变换［11］，算法流程如下：

step1：轮密钥加，将当前分组和扩展密钥的一部分进行按位异或操作；

step2：字节替代，使用s盒［12］中与数据块对应行和列的数据替换原数据，即完成分组的字节到字节的代替；

step3：行位移，数据块第一行不变，第二行左移一位，第三行左移两位，第四行左移三位；

step4：列混合，将数据块每列的字节通过线性函数结合起来。

128bit密钥长度的AES算法需要进行10轮迭代，加解密过程中除了轮密钥加不同，其余操作均取逆。

3.3 SHA-1算法设计

SHA-1算法流程如下。

step1：假设有长度为l位消息M。为了使消息长度是512的整数倍，需要将消息进行填充操作。将一个1、k个0和l的二进制表示的64位追加到消息后面。如式（6）所示：

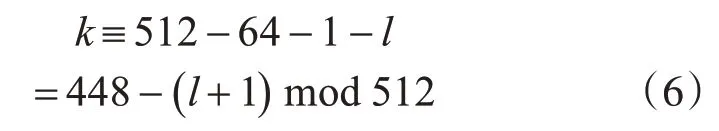
在使用压缩函数前，需将消息分割为长度512位的分组M1，M2，…，Mn，每个512位分组分为16个32位的单词。如式（7）所示：

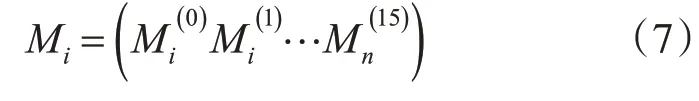
step2：在哈希函数计算中，对每个消息分组Mi进行四个阶段处理，每个阶段20轮，每轮都计算一个32位 单 词［13］，即W0，W1，…，W79。最 终 得 到160bit消息摘要值。

3.4 混合加解密算法设计

混合加解密算法过程如图3所示。

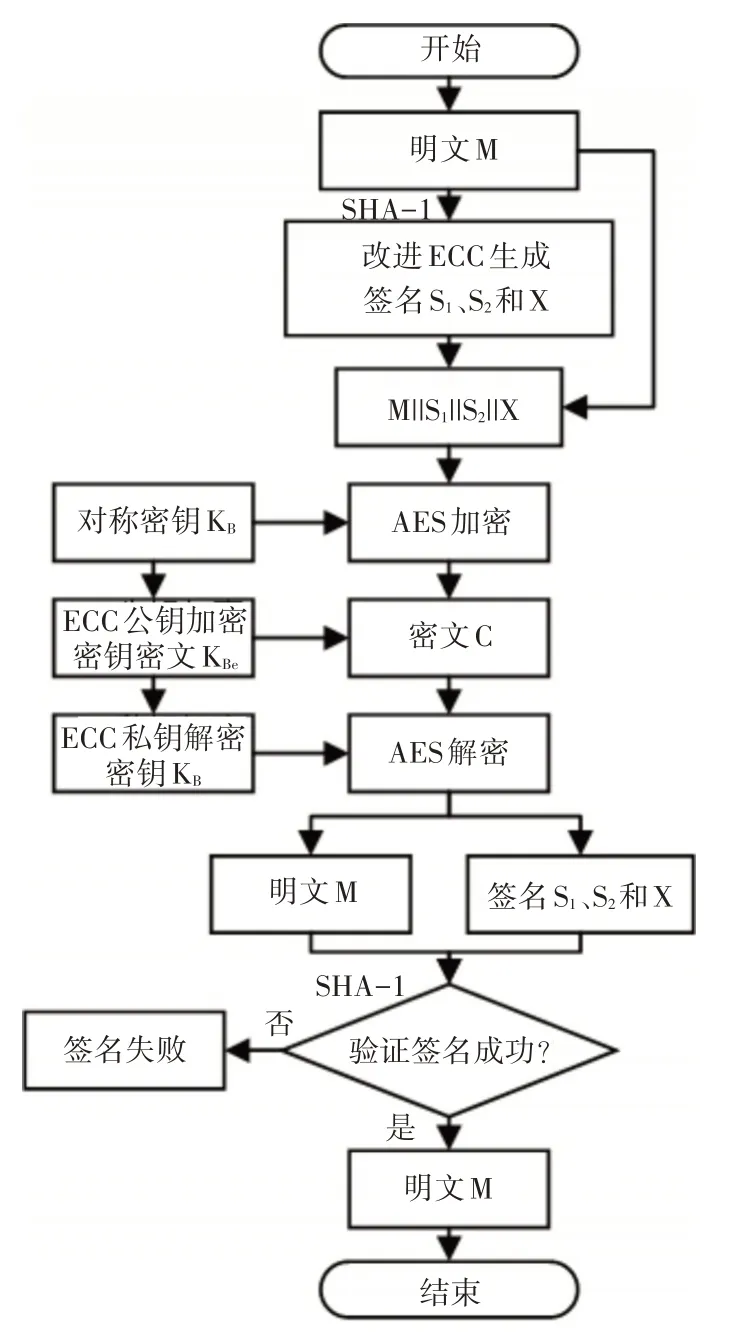
图3 混合加解密算法流程图

具体混合加解密算法流程如下：

step1：使用SHA-1哈希算法生成消息摘要H，再使用改进ECC数字签名算法私钥加密生成数字签名s1和s2，并生成验证值x；

step2：将明文M、数字签名s1、s2和x拼接，使用AES算法加密生成密文C；

step3：将密钥kB使用ECC算法公钥加密生成密钥密文kBe，将kBe和密文C发送给接收端；

step4：接收端收到消息后，使用ECC私钥解密密钥密文kBe，得到对称密钥kB，使用AES算法解密密文C，得到明文M、签名s1、s2和x；

step5：使用SHA-1验证明文M完整性，使用改进ECC公钥验证签名，验证成功，则所得到的明文M有效可用。

4 实验结果与分析

4.1 实验结果

首先使用哈希函数对工业互联网中设备信息、实时数据等进行哈希操作，获得消息摘要，再使用改进ECC私钥加密消息摘要生成数字签名。最后使用AES算法对已签名明文进行加密［14］。图4为生成数字签名和混合加密结果的终端打印信息，图的上方为明文信息，中间为数字签名的摘要值和签名信息，下方为密文信息。

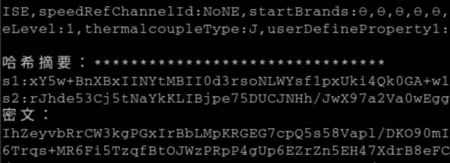
图4 生成数字签名并加密结果图

图5为验证签名和解密结果的终端打印信息，图的上方为密文信息、中间为验证签名的摘要值和验签成功提示，下方为解密后明文信息。

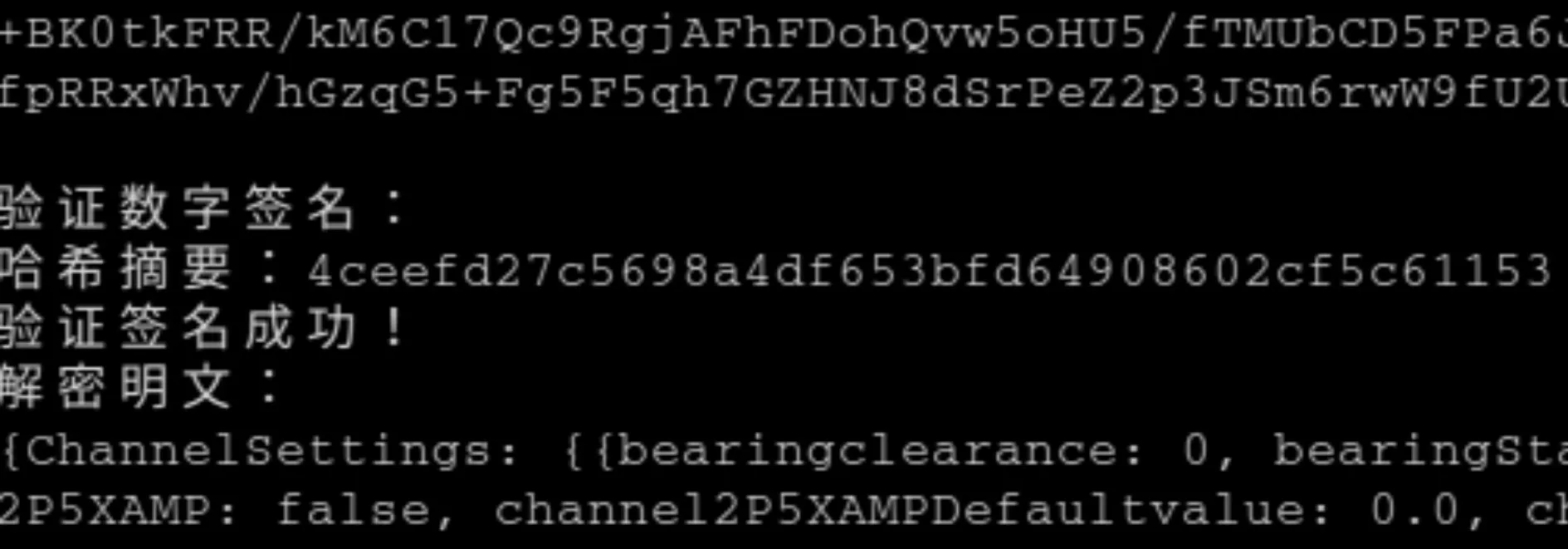
图5 验证数字签名并解密结果图

4.2 性能分析

1）加密性能分析

表1列出了加密不同大小数据包时，使用AES加密、RSA+AES混合加密和ECC+AES混合加密的加密耗时。从表格可以看出，AES算法的耗时最短，而其他两个混合算法的加密耗时区别较小。但是ECC算法在安全性上比RSA算法更好，且密钥更易于管理。数据波动图如图6所示。

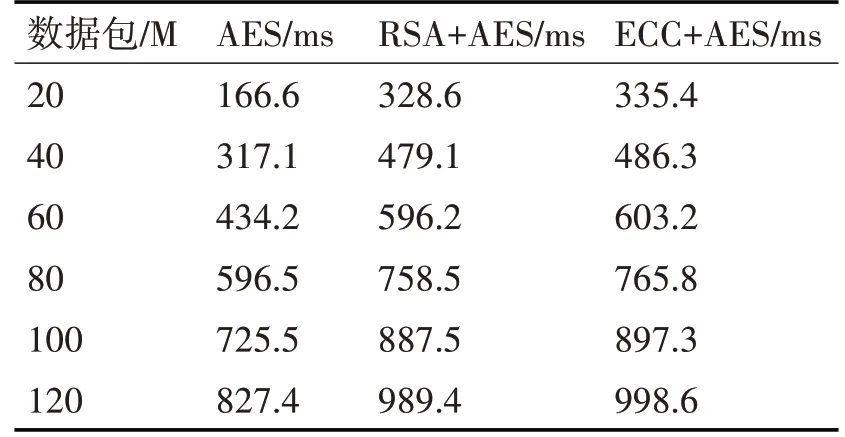
表1 不同算法加密时间比较表

图6 不同算法加密时间对比图

2）解密性能分析

表2列出了不同算法解密时间值，从表格可以看出，三种算法的解密时间与加密时间相比差距较小，其中AES算法解密耗时最短，而其他两种混合算法的解密耗时几乎一致。数据波动图如图7所示。

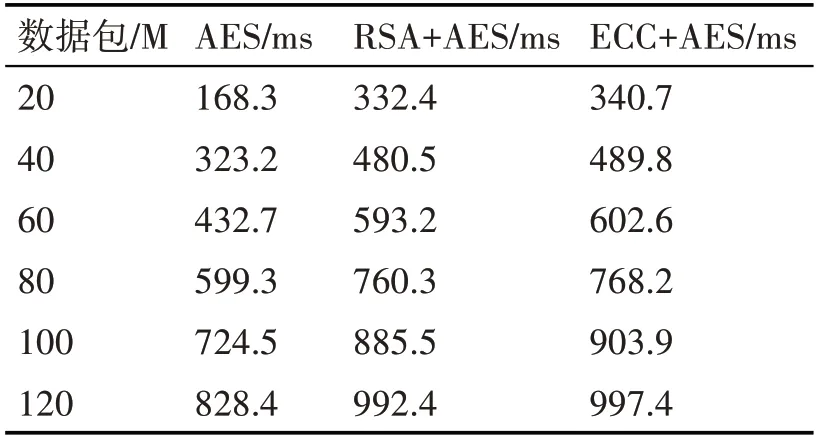
表2 不同算法解密时间比较表

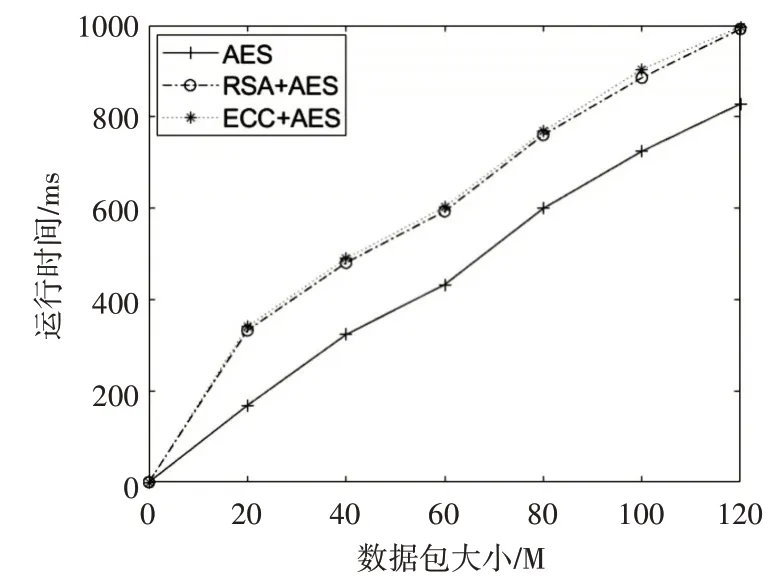
图7 不同算法解密时间对比图

3）数字签名性能分析

对边缘数据中的指令数据和配置数据要求数据能够被完整传达和发送者的身份能够准确核实。因此需要对该类型数据进行数字签名操作。表3列出了采用原ECC算法、RSA算法和改进后的ECC算法进行数字签名的耗时。

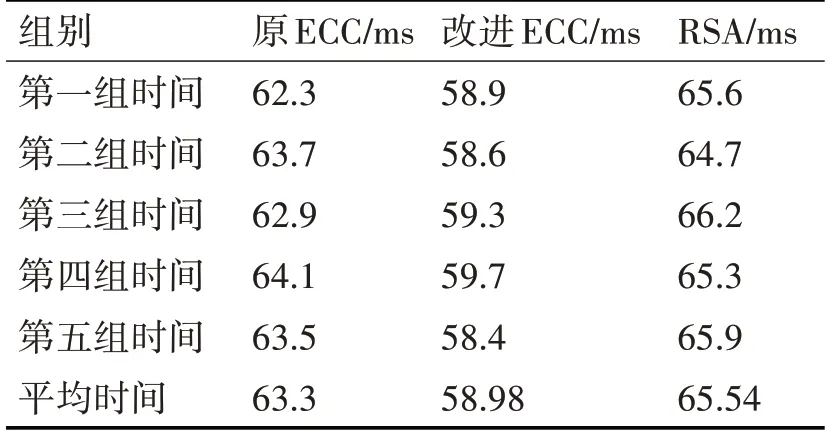
表3 不同算法数字签名时间比较表

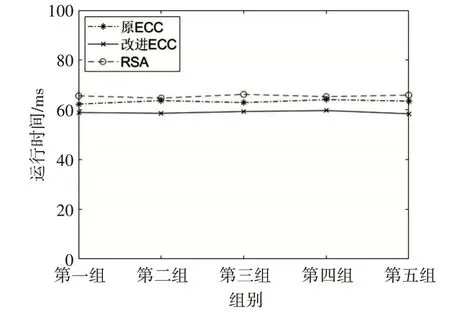
图8 不同算法数字签名时间对比图

由于数字签名采用公钥密码技术的私钥加密消息摘要值，而在安全等级相同的情况下，ECC密钥长度更短，加密速度更快，更便于存储。因此在测试不同算法的数字签名时间中，由于RSA私钥比公钥长度更长，因此加密速度慢，且密钥较长不便于存储。而改进ECC数字签名算法更是比原ECC速度更快。证明了本文改进的ECC数字签名算法对提升数字签名时间是有效的。

AES算法加解密速度较快，确保了对实时数据的实时加密与解密，ECC算法安全性较高，用其加密对称密钥确保的密钥的安全分配，因此在数据安全和密钥安全方面，此种混合加密方案具有较高的安全性。由于ECC的公钥是公开传输，某些攻击手段［15］可以根据公钥推算出私钥，本文中使用双私钥数字签名操作，确保了私钥的安全性。

5 结语

针对工业互联网中边缘数据的安全问题，本文采用了混合加密的方式对边缘数据进行加解密操作，采用了改进的椭圆曲线数字签名算法进行了数字签名操作，并设计了一个完整的工业边缘智能终端安全系统，实现了边缘端数据的安全存储和传输。由于边缘端环境复杂，仅仅依靠数据加密一种方式实现边缘端设备的安全防护还不够，还需要考虑边缘设备中系统的安全性，可建立入侵检测机制进行系统的安全防护，这也是下一步需要研究的方向。