无人机室内自主定位方法研究*

王晶晶 顾 德

（江南大学物联网工程学院 无锡 214122）

1 引言

随着科技的发展，无人机逐渐走进人们的视野。无人机具有隐蔽性好、机动性强、成本低等优点，在军事和民用领域被广泛应用［1］。目前，市售的无人机定位方式大多使用GPS与惯性测量单元（Inertial Measurement Unit，IMU）结合的方法［2］。这种常用的定位方式在室外无遮挡的环境具有较高的定位精度，而在较为复杂的室内环境中，GPS易受干扰，信号不稳定，若仅依靠IMU进行定位，其定位误差会随时间的增加而增大。随着机器视觉与图像处理技术的深入研究，相关技术逐渐被应用在无人机定位领域。视觉定位方法具有定位设备可靠，设备依赖性较小［3］，而且定位误差不随时间增加而增大的优点。本文根据以上视觉特点，提出一种基于双目视觉的无人机自主定位方法，通过机载双目摄像头采集地标图像，经过双目校正，特征点匹配等图像处理方法计算深度，并利用坐标变换得到无人机空间位置［4］。所有工作均由无人机及其装载设备完成，因此具有自主性。此外，相较于使用外部视觉传感器定位的方法，此方法还具有灵活性好，成本低，抗干扰性强等优势。

2 地标设计

室内定位中常用的地标有双圆地标，4圆形地标，H型地标，7个简单多边形的组合地标［5］等。本文设计T型地标［6］并将其作为室内定位标志物的原因如下：1）文中提取的特征为点特征，为保证无人机空间坐标计算的正确性以及无人机飞行方向的确定性，提取到的特征点应分布较好且个数适量。通过对比各地标的特征，T型地标满足此要求（圆形地标和H型地标有多条对称轴不易判断无人机飞行方向）。2）本文使用机载芯片进行图像处理，计算能力有限，T型地标由两个矩形组成，棱角分明，容易提取特征点（多边形组合定位角点提取较为复杂）。T型地标如图1所示。

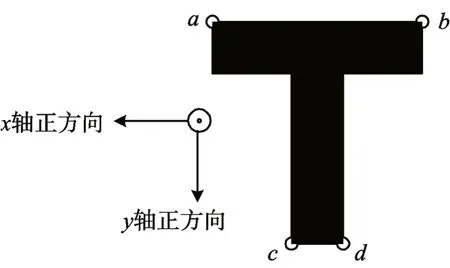
图1 T型地标示意图

通过地标尺寸实验得出地标尺寸对定位精度的影响较大，因此为保证无人机在室内飞行时得到较为清晰完整的地标图像，本文选取T型地标尺寸为长10 cm、宽2 cm的矩形。以地标左上角角点a为坐标原点，其余角点坐标值分别为b（-100，0，0）、c（-40，120，0）、d（-60，120，0）。

3 双目系统测量原理

双目测距原理是利用两个摄像机对同一目标进行拍摄，通过提取、匹配左右图像对应特征点得到目标物在图像中的视差，最终得到目标物的深度信息［7～9］。理想的双目立体成像原理如图2所示，左、右摄像机光轴相互平行，相机坐标系的原点为Ol、Or，分别在各自的光心处，光心距为B。以两个坐标系原点的水平连线方向为相机坐标系的Xc轴，以平行图像平面垂直Xc轴方向为Yc轴，Zc轴垂直于XcYc平面，符合右手定则。

图2 双目立体成像原理图

设左右摄像机在同一时刻观察空间物体某一特征点P的坐标为(X，Y，Z)，点P在左右摄像机成像平面上的投影点坐标分别为pl(xl，yl)，pr(xr，yl)。

根据双目立体成像原理可以得到深度Z与视差d的几何关系，其表达式为

其中：视差d=|xl-xr|；Z为点P距摄像机的垂直距离，即深度；B为两个相机的光心距；f为相机焦距。

则三维空间内一点P(X，Y，Z)的坐标表示为

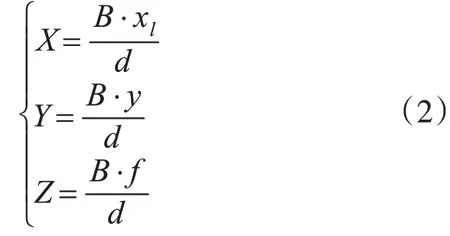
由式（1）可知，在光心距B和焦距f等摄像机结构参数不变的情况下，空间任意点P距摄像机的垂直距离与视差d成反比。即左右相机的成像图像中视差值越小，物体距离摄像机越远。得到深度距离后，即可通过坐标系转换求得空间点的三维坐标。

4 无人机三维定位流程

无人机实现室内的精准定位需进行以下几步：1）将两个相同的摄像头安装在无人机底部采集图像，选取T型地标左上角角点作为坐标原点；2）对双目摄像头进行标定，得到双目摄像头的内部参数以及两相机在世界坐标系下的空间位置关系等；3）根据极线约束准则对图像进行校正，以达到左右图像共面同行的情况；4）将双目校正图像进行地标检测、特征点提取及特征点的匹配；5）计算视差并根据视差结果计算深度以及坐标原点相对双目视觉的空间位置，利用坐标系转换最终求得无人机相对于地标的室内空间位置。无人机定位的流程如图3所示。

图3 无人机三维定位流程图

4.1 双目摄像机标定

摄像机标定的目的是建立摄像机成像模型，获取相机的内外参数，以便建立世界坐标系下物体空间点与图像对应点之间的关系［10］。

标定方法采用基于平面标定模板的张正友方法，该方法从不同角度、距离采集棋盘格图像，依靠多幅图像对应点之间的坐标关系进行参数解算。通过相机标定可求得摄像机的内部参数M、畸变矩阵D以及摄像机的外部旋转矩阵R和平移矩阵T：

其中：fx、fy分别为图像平面水平、竖直方向的焦距；u0、v0表示图像的中心像素坐标；k1、k2、k3为相机镜头的径向畸变系数；p1、p2表示相机镜头的切向畸变系数。

假设世界坐标系为Ow，摄像机坐标系为Oc，空间点P在Ow和Oc坐标系下的空间坐标分别为Pw和Pc，则Pw和Pc之间的关系式为

其中：R是一个3×3的矩阵，表示世界坐标系下右相机相对于左相机的旋转矩阵；T是一个3×1的矩阵，表示世界坐标系下右相机相对于左相机的平移矩阵。

实验采用文献［11］的方法对双目视觉系统进行标定，并利用Matlab中的标定工具箱进行标定。

4.2 基于标定技术的双目校正

由于工艺水平的限制，现实中大多数双目摄像机成像平面的空间位置无法达到光轴平行的情况，因此需要对摄像机采集的图像进行立体校正从而构造出理想的双目模型［12］。本文采用Bouguet算法［13］进行校正，其核心思想是使两图像中的每一幅重投影次数最小化，同时使观测面积最大化。校正步骤如下。

1）将右图像平面相对于左图像平面的旋转矩阵R分解为两相机的合成矩阵rl、rr，每个相机都旋转一半，以达到图像共面的目的。

2）为了将左相机极点变换到无穷远，并使极线水平对准创建一个由极点e1方向开始的旋转矩阵Rrect，以实现行对准的效果。

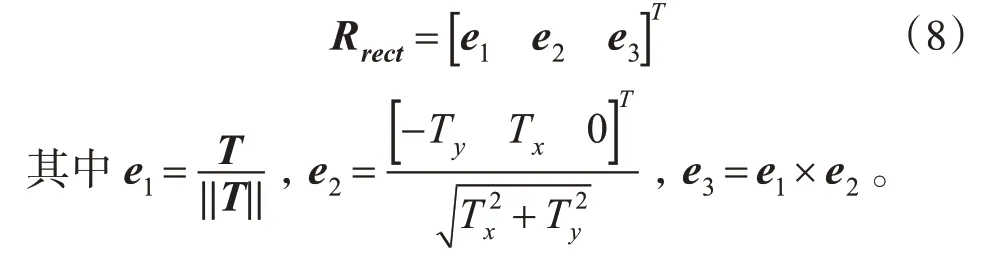
3）通过合成旋转矩阵与变换矩阵相乘获得左右相机的整体旋转矩阵。左右相机坐标系乘以各自的整体旋转矩阵就可使得左右相机的主光轴平行，且像平面与基线平行。

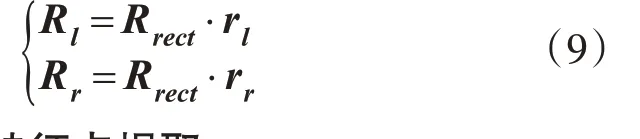
4.3 地标检测与特征点提取

地标检测目的是从机载相机获取的地面图像中去除多数干扰部分，分割出T型地标［15］。地标检测与分割使用二值化方法，根据地标和背景的区别选取合适的阈值，文中采用的地标为黑色，因此应选较小的阈值，由多次实验验证，阈值宜取50。

对分割出的地标图像进行特征点提取［14］，如图1所示。本文选取a、b、c、d四点作为图像特征点，原因如下：1）由式（1）可知，光心距B和焦距f确定时，深度Z的精确度取决于视差d，选取多个特征点计算多组视差可提高视差的精确度，减少随机误差；2）选取T型地标的4个端点作为特征点，相较于地标中其他点更易提取。

4.4 视觉三维坐标解算

双目视觉的视差由左右图像匹配点在图像物理坐标系下作差得到，而上述匹配点得到的视差值是在像素坐标系下求得，因此需要知道像素坐标系与图像物理坐标系的转换关系［16］。假设图像中一个像素在图像物理坐标系下水平和垂直方向的物理尺寸为dx和d y，则图像物理坐标系与图像像素坐标系的转换关系表示为

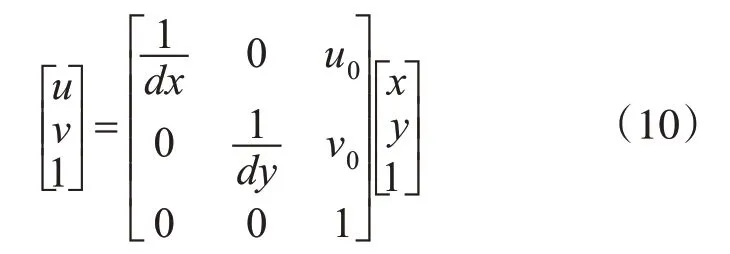
其中：[uv1]T是像素坐标点的齐次坐标，[xy1]T是图像物理坐标点的齐次坐标。

由上述转换关系即可得到视差在图像物理坐标系与在像素坐标系下的关系式：

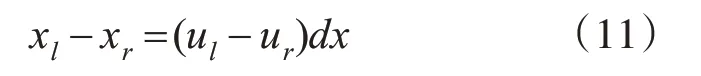
本文以T型地标的左上角角点为参考原点，将等式（11）代入等式（2），则室内无人机的空间位置坐标为

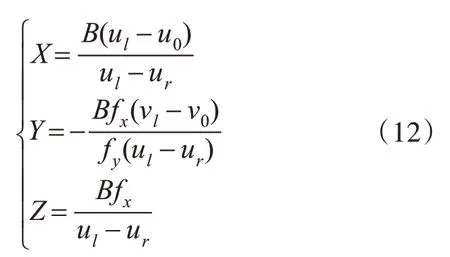
5 实验

本文系统采用单片机STM32F767作为机载芯片，完成双目校正、图像处理以及三维坐标解算。图像采集模块为OV2640双目摄像头，其分辨率为320像素×240像素，光心距为60mm。

1）对摄像机进行标定。标定板使用角点数为8×6，边长为24.5mm的棋盘格。双目摄像头标定结果如表1；

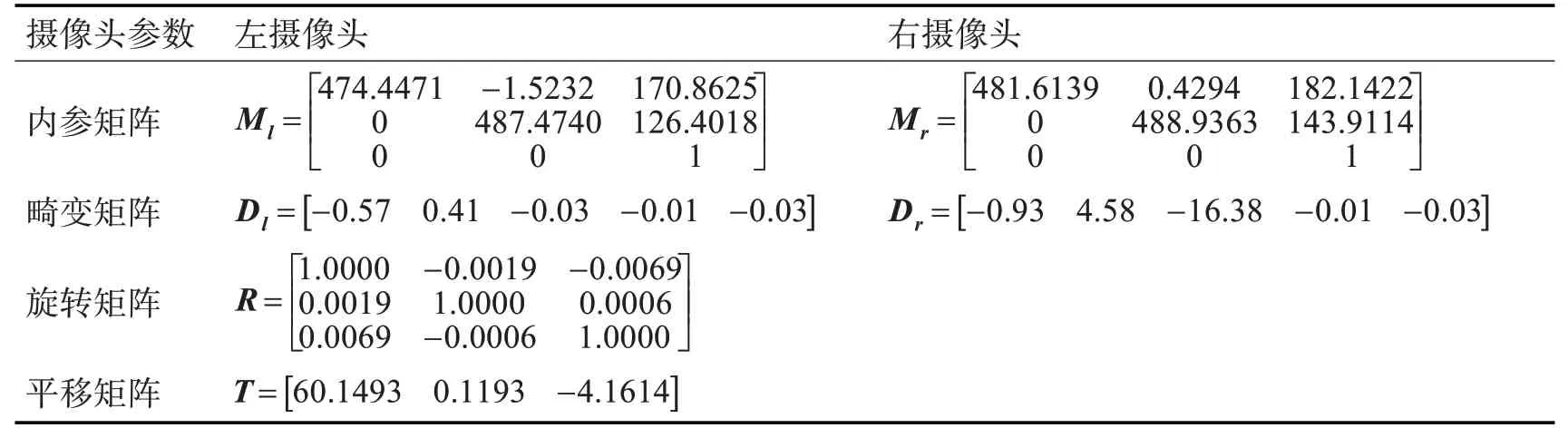
表1 双目摄像头标定结果表

2）地标尺寸比较实验。本文分别选取长10cm、宽2cm与长15cm、宽3cm的两种矩形进行测距对比实验，表3为长15cm、宽3cm的矩形的测距结果。

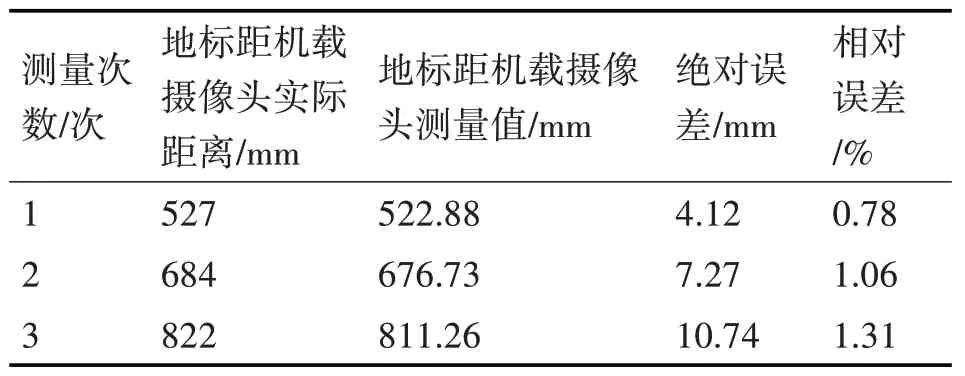
表3 长15cm、宽3cm矩形测距结果

对比表2与表3结果可以看出，选择更大尺寸的地标将提高测量精度。而当无人机距离地标距离过近时，双目相机的成像图像如图4所示，此时对应角点缺失较多，容易出现特征点误匹配的错误，影响定位效果。

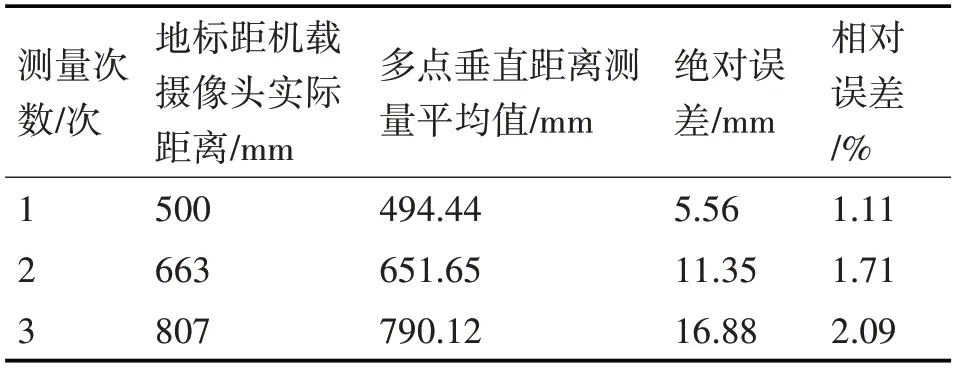
表2 长10cm、宽2cm矩形测距结果

图4 大尺寸地标成像图

3）无人机在室内飞行时，由于双目摄像头广角的局限性，地标并非完全在双目摄像头的视野范围内，角点缺失的地标图像如图5所示。本文以图5（a）为例，针对角点缺失情况设计以下处理方法：（1）计算地标左右图像中ab与a'b的像素长度lenab、lena’b；（2）设定阈值Th并计算l enab与lena’b的差值判断图像是否存在角点缺失；若lenablena’b＞Th，则为角点a缺失，舍弃角点a，计算b、c、d三点的测距平均值；否则判定该地标图像为完整图像。本文将阈值设置为5。

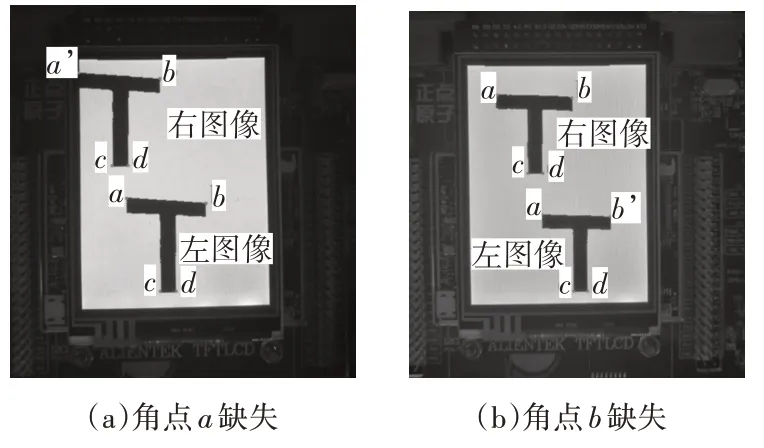
图5 地标角点缺失图

4）无人机三维坐标定位实验。由式（12）得到无人机相对于角点a的三维空间坐标如表4所示。

表4 无人机相对点a的坐标测量结果

由表5可知，使用本文算法测量的无人机位置与其真实位置相近，验证了本文算法的精确性。

表5 点a空间坐标误差

6 结语

本文提出一种结合T型地标，使用双目相机实现无人机室内定位的方法，改善了室内GPS信号弱无人机难以定位的缺点。此方法具有成本低，不受电磁干扰，灵活性高，移植方便等优势。结果表明：本文提出的自主定位方法与无人机的实际位置匹配精度高，定位效果较为理想。但由于单个STM32F7的处理速度有限，目前无人机的图像处理速度为10帧/s，较难满足无人机定位的实时性要求。下一步的研究方向为将此种定位方法与惯性传感器融合得到实时并且准确的室内无人机位置信息。