摸石头过河算法解决车间调度问题的研究*

许彦辉 高 尚

（江苏科技大学计算机学院 镇江 212000）

1 引言

作业车间调度即Job-Shop调度问题，是典型的多目标问题，很多研究学者都会将其作为生产调度问题［1～4］，对于企业复杂的生产调度环境，作业生产调度是一种简化模型。对该调度模型的研究具有实际的理论意义和研究价值。作业车间生产调度是指每个生产作业需要在多台加工机器上进行加工。每个生产作业包含多个生产过程。工件一经加工，不得中断。每个生产作业都有自己的处理顺序，不限制作业处理的机器，一个生产作业可以有不同的处理路径，一台机器一次只能处理一个作业。在这种生产车间中，机器的布局是任意的，工件的加工机器也是任意的，每个工件的数量和加工顺序也是任意的，每个产品都有其不确定的加工路径。由于作业加工的多重约束和加工环境的随机不确定性，它已成为一个极其困难的NP完全问题。传统多目标优化算法有加权法求和法［5～6］、约束法［7］、目标规划法［8～9］和目标满意法［10］等。近些年研究比较热门的多目标遗传算法［11］、蚁群算法［12］、粒子群算法［13］等也是用来解决最优化问题。

“摸石头过河算法”在2015年被高尚、邱玲、曹存根等率先提出。2015年3月，高尚、邱玲、曹存根在《南京师范大学报》自然科学版发表《解连续性优化问题的摸石头过河算法》的学术研究文章，受到摸石头过河思想的启发，提出了摸石头过河算法［14］，同时通过仿真实验，验证了其具有搜索速度快、精度高和不易陷入局部极值点的特点，进而说明该算法具有较好的全局搜索能力，应用前景非常广泛，具有一定潜力［15］。

摸石头过河算法提出时日尚短，但其也已经具有极大的优越性，并且经过数年的发展，也获得了一定的改进，对于连续优化问题与离散优化问题都能取得较好的优化结果［14］；将摸石头过河算法应用在解决实际的多目标车间调度多目标优化问题中，首先对FT06的标准问题进行求解优化，然后考虑到实际生产中存在工件在机器间的运输时间问题，将其考虑在内，继续优化带有运输时间的FT06标准问题，均优化得到最优解［14］。

2 摸石头过河算法

摸石头过河算法的思想来源于“摸石头过河”的思想［16］：摸到一个“石头”后，向该“石头”周围摸索其它石头，当再摸到一个“石头”后，再向该“石头”周围摸索其它石头，以此类推进行搜索。摸石头过河算法以一个解为起点，向该起点附近邻域随机搜索若干个解，找出这些解中的最好的一个解，以此解作为第2次迭代的结果。然后以此点为起点，再向附近邻域随机搜索若干个解，找出这些解中的最好的一个解，以此解作为第3次迭代的结果。后面的步骤以此类推，直到达到最大迭代次数或其它停止条件为止。其迭代过程如图1所示。

图1 摸石头过河算法迭代过程

摸石头过河算法是一个寻解与迭代的过程。由于算法每一次寻解都只保留最好解，所以在迭代的正反馈作用下，函数目标函数值将趋向于该函数的最小值。具体算法流程为［14］

3 多目标摸石头过河算法

3.1 算法模型

对优化多目标问题可表示为

其中，x=(x1，x2，…，xn)∈X∈Rn，n为变量的维数，X为决策空间；y=(y1，y2，…，ym)∈Y∪Rn，m为目标函数个数，Y为目标空间；gi(x)≥0(i=1，2，…，p)为p个不等式约束；hj(x)=0(j=1，2，…，q)为q个等式约束。

当目标函数处于冲突状态时，即不存在最优解使所有目标函数同时最优化。此时，把m个目标集成在一起，构成一个实质偏好函数，即构造一个妥协模型。然后在相同条件下，极大化妥协模型函数，得到的函数解成为妥协解，并作为实际意义上的原多目标问题的Pareto有效解［14］。

采用加权求和你法构造多目标优化问题的妥协模型。设目标函数fj(x)的优选权系数分别为λj，其中，j=1，2，…，m，则可以构造如下综合评价目标函数［14］：

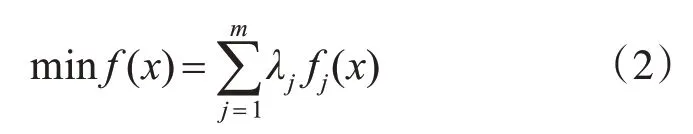
其中，0≤λj≤1，且λ1+λ2+…+λm=1。然后利用摸石头算法进行求解。

3.2 多目标摸石头过河算法流程

本文提出求解Pareto最优解的多目标的摸石头过河优化算法，具体流程如下：

1）随机产生N个初始可行解X1，X2，…，XN以及m个权值λ1，λ2，…，λm，其中0≤λj≤1且λ1+λ2+…+λm=1，评价各独立优化目标fj以及综合目标将p个可行方案的综合目标值，确定为当前最佳方案最佳解X，令k=0。

2）由当前解X通过邻域函数生成p个新的可行搜索解，并对其优化目标和综合目标进行评估。

3）对比全部的综合性的目标，如果存在这种

FX＜FX，那么用X'代替X成为新的当前解。

4）判断是否满足终止条件，否则令k=k+1，返回步骤2）。

上述算法过程保留了传统的摸石头过河算法的特点，并采用加权综合目标对多目标优化进行评价。由于权重的随机性，该算法的多次运行或并行实现可以在Pareto边界上获得多个方向的Pareto最优解，为决策者提供多个选择。应该强调的是：

1）步骤1）中，产生N个初始可行解，由于初态的随机性，当数量N足量多时可一定程度上体现了整个解空间中状态的分布情况。

2）摸石头过河算法区别于传统规划算法的关键之一在于邻域函数的设计。一般地，可以简单采用附加Gaussian分布扰动方式，即x'=x+ηξ，ξ∈N(0，1)，η为步长。最优解的保留则能够避免优良解的遗失。

4 仿真实验结果与分析

本文主要是在Matlab环境下进行的实验分析，通过比较算法求解多目标优化问题的结果，对影响寻优结果的邻域解搜索方法进行了讨论，确定了较好的邻域解搜索方法。其中选择的标准算例是车间调度问题FT06。

4.1 实际问题介绍

为了判断算法的优缺点，需要用同样的问题去测试，这些测试问题逐渐形成了标准问题。最著名的标准问题是Fisher等［17］提出的FT问题，包括FT06（6×6，即为6个工件，每个工件有6道不同的加工工序）、FT10（10×10）和FT20（20×5）。本文中采用FT06标准问题对多目标摸石头过河算法的可行性进行分析研究。FT06问题描述见表1，其中的序列对（M，T）表示（机器，加工时间）［14］。

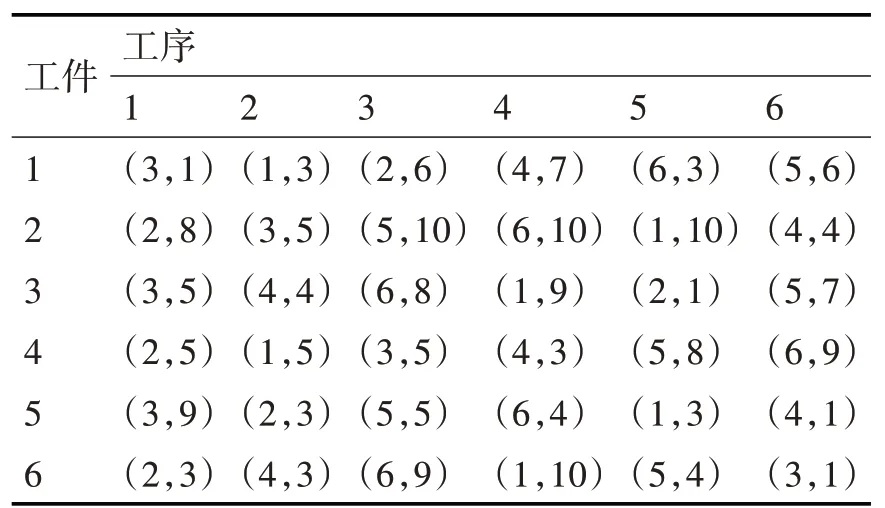
表1 标准问题FT06

FT06问题的描述可见图2。工件P1在机器M3上加工，生成节点11，1个单位时间后，节点11消亡，工件P1在机器M1上加工3个单位时间。6个工件的加工过程形成了生产现场的6个线程［14］。

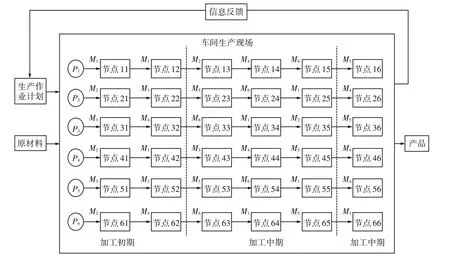
图2 生产过程示意图

在实际生产现场，往往要考虑到工件之间的物流时间，则标准问题便会被复杂化。以某叶片车间生产制造现场为例，其加工机器布局如图3。工件在各个机器之间的物流时间用矩阵表示为［14］

图3 机器布局图

其中Aij表示工件从Mi运输到Mj所需的时间。

设置迭代寻优次数为100，通过加权求和法构造综合评价函数，共有两个优化目标，为机器工作时间为Cmax和机器工作空闲时间Wmax，机器工作时间权值设为λ，分目标的权值之和为的原则即则机器工作空闲时间权值为1-λ，得到构造的综合评价函数为F=λ*Cmax+(1-λ)*Wmax［14］。

为了分析多目标摸石头过河算法的性能，我们通过针对性的几点讨论来分析所提出算法的性能，主要是通过加权求和法构造的综合评价函数中权值对算法优化的影响，以及多目标摸石头过河算法在增加运输时间的标准问题FT06上的优化性能［14］。

4.2 综合评价函数构造中权值的影响

在多目标摸石头过河算法优化过程中，综合评价函数对优化的结果至关重要，这里我们讨论了多目标中各分目标的不同权值对优化结果的影响，车间调度算法中主要优化的两个目标：机器加工的最大时间Cmax以及机器工作空闲时间Wmax，通过加权求和法得到综合评价函数F=λ*Cmax+(1-λ)*Wmax，为了公平比较，对每个权值求和得到的评价函数优化时各做了500次实验［14］，从中得到的最优结果为

λ=0时，F=87，其中机器加工最大时间55，机器空闲时间87；

λ=0.25时，F=79，其中机器加工最大时间55，机器空闲时间87；

λ=0.5时，F=71，其中机器加工最大时间55，机器空闲时间87；

λ=0.75时，F=63，其中机器加工最大时间55，机器空闲时间87；

λ=1时，F=55，其中机器加工最大时间55，机器空闲时间99。

具体优化结果可见表2。从最优结果中，可以看出除了λ=1时，其余权值情况下优化得到的机器加工最大时间与机器空闲时间是相同，然而由甘特图也可以看出，最终优化得到的加工顺序确实不同，优化的综合评价函数值相同，这也说明该问题具有很多个最优解，而不同权值的优化方式都是可以优化到最优值的，多目标摸石头过河算法是可以优化FT06问题得到最优解的［14］。

表2 不同权值下的综合评价函数优化结果

4.3 增加工件运输时间对寻优的影响

在实际的车间生产过程中，工件在机器之间的加工转运往往也要花费一定的时间，因此在实际的调度优化中需要考虑到运输时间的存在，本节将运输时间引入到我们的优化问题中来，机器间工件的运输时间可见4.1节矩阵A，机器位置布局见图3［14］。

同样地，经过以上几节的实验研究，在加入工件运输时间后，设置参数为取权值λ=0.5构造综合评价函数F=0.5*Cmax+0.5*Wmax，初始解的搜索个数为10000，邻域解的搜索方法采用三种方法随机选择混合的方式，每次迭代的邻域解搜索个数为100，迭代总次数为100，共进行500组实验。500次实验中，优化得到的最优值为89，最劣值为102.5，500次实验结果的平均值为92.161，该问题的最优值也为89，根据实验结果可以看出加入工件运输时间以后，优化问题变得更复杂，多目标摸石头过河算法依然能够优化得到最优值。由一组最优值编码201520310255342514013341041235442503，表3列出了该方案的机器加工时间，表中数字含义与表1相同，图4同时也展示了该加工甘特图［14］。

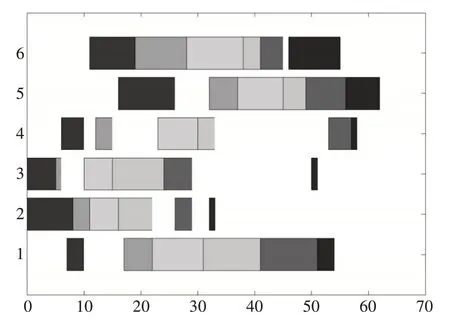
图4 增加运输时间的FT06问题最优解甘特图

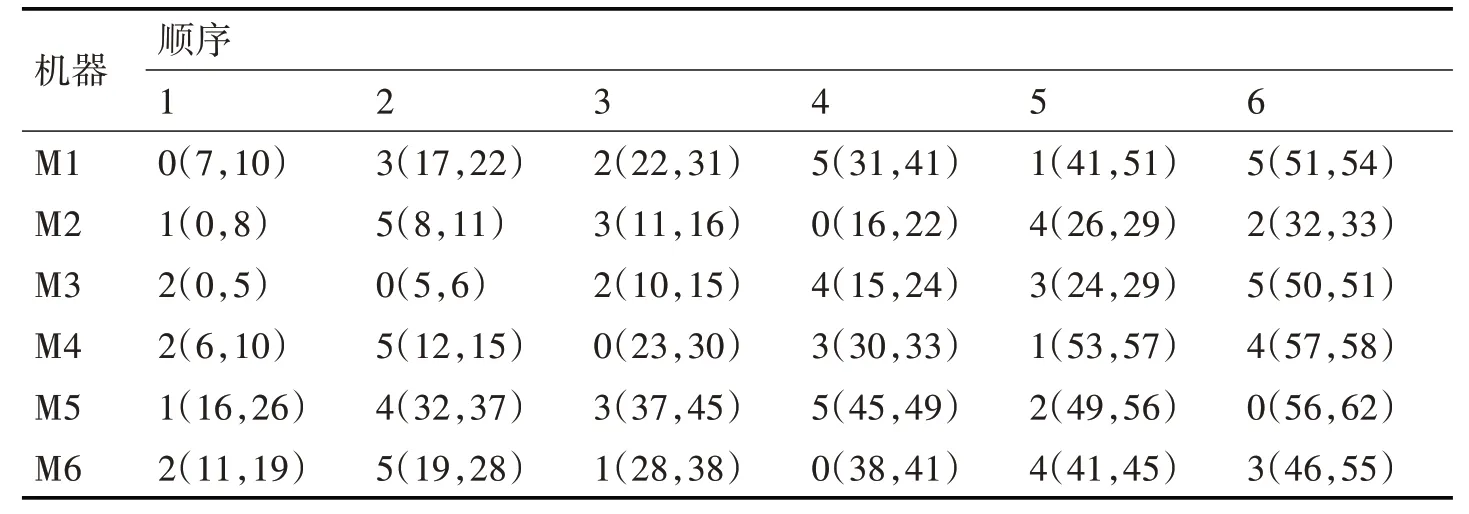
表3 增加运输时间的FT06问题机器加工时间表

5 结语

多目标优化问题被应用于生产和生活的各个方面，对作业车间调度问题的深入研究具有重要的理论意义和应用价值。寻求高效稳定的调度算法是制造业和人工智能领域共同研究的重点。基于Job-Shop调度问题具有深远的研究意义，提出了一种简单有效的摸石头过河算法对其进行优化。摸石头过河算法本身对于连续优化和离散优化问题的优化具有一定的优势。在多目标优化问题的基础上，提出了一种多目标摸石头过河算法对其进行优化。优化过程相对简单，但效率高，可以简单地找到最优解，通过仿真验证了该算法的可行性和有效性。