载体运动下光伏组件最大功率点动态跟踪方法*

李培兴 彭乐乐 张亚飞 陶俊鹏 郑树彬

（1.上海工程技术大学机械与汽车工程学院 上海 201620）（2.上海工程技术大学城市轨道交通学院 上海 201620）

1 引言

光伏发电技术是一种零碳发电技术，是实现国家2030年碳达峰和2060年碳中和的关键发电技术之一。随着海上光伏电站、移动载体分布式供电模式的推广，运动状态下光伏发电已经成为光伏发电中一种重要的应用方式。然而，光伏电池的输出功率随外界光强及温度的影响而不断改变，为了最大化的利用光伏能量，需要对光伏电池进行最大功率点跟踪（Maximum Power Point Tracking，MPPT）。长期的实践表明，光伏发电系统采用MPPT算法，其输出电能可以提高30%～40%［1～3］。

MPPT算法多达十几种［3～4］其繁衍出来的算法更是超过几十种。从算法的复杂维数来看，可以将其分为直接MPPT算法，解析MPPT算法和智能MPPT算法。直接MPPT算法［5～6］主要是利用组件最大功率点与其开路电压或者短路电流之间存在近似比例关系而将其控制在固定的工作点，这类算法中比较典型的有开路电压法和短路电流法［5］，其优点是控制简单成本低，缺点是效率低。解析MPPT算法是利用光伏电池的输出极值特性，利用数值计算的方法获取极值点，该类方法中主要有扰动观察法［7］及增量电导法［8］，其优点是效率高，缺点是抗干扰能力不强。实现更高效率的智能MPPT算法便诞生了，该类算法通常采用智能运算和求取光伏电池的功率最大点，较为典型的有粒子群算法［9～10］，神经网络算法［11］等。该类算法可以减小对光伏电池的依赖程度，甚至还可以通过不断的训练学习达到自我完善的效果。但是该类算法的缺点是需要大量的计算数据，不利于光伏发电技术的低成本推广和应用。

然而，以上MPPT算法中针对载体运动状态的光伏组件最大功率点动态跟踪方法研究较少。为了实现运动状态光伏组件高功率发电的目的，本文通过利用惯性测量单元获取组件运动姿态，并构建坐标映射关系，实现载体坐标与大地坐标间的转换，将运动姿态转换为光强变化。利用光伏五参数模型及环境参数关系，建立了光伏组件动态模型。基于此提出了一种自适应动态光伏组件最大功率跟踪算法。

2 载体运动下光伏组件动态模型

图1为载体运行状态下光伏组件动态建模方案图，通过利用惯性测量单元测量载体的运动姿态，构建载体坐标系与大地坐标系转换矩阵获取光伏组件光强姿态角变化，采用光伏组件五参数数学模型及环境参数与光强关系，获取光伏组件动态模型。

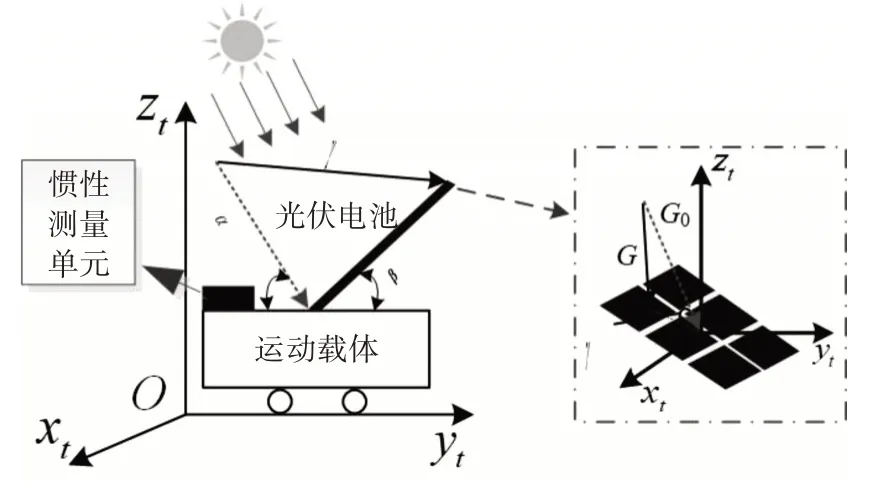
图1 载体运动状态下光伏组件动态模型

设定载体的运动姿态状态矩阵M为

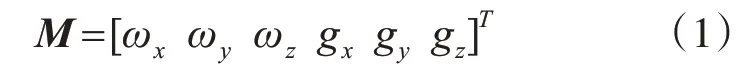
其中，ωb为陀螺仪所测运动载体在载体坐标系下角速度输出值，ωb=[ωxωyωz]T，gb为加速度计所测运动载体在载体坐标系下加速度输出值，gb=[gxgygz]T。根据欧式空间旋转理论，载体坐标系向大地坐标系转换得到大地坐标系下运动姿态如式（2）：

其中，IL为光电流，IO为光伏电池反向饱和电流，US为光伏电池的输出电压，q为电荷常数，K为玻尔兹曼常数，n为二极管理想因子，T为电池温度，RS为电池串联等效电阻，RP为电池并联等效电阻，ILr为在标准测试条件（T=25℃，S=1000 W/m2）下光生电流，ki为电流温度系数，T为温度，Tr为标准测试条件下温度值，S为光照强度，Sr为标准情况下的光照强度，Ior为标准测试条件下的二极管反向饱和电流，EG为光伏组件中半导体禁带宽带。

3 光伏组件自适应最大功率点跟踪算法

光伏组件自适应最大功率点跟踪时间Tpv和步长U之间可以用比例关系表示为

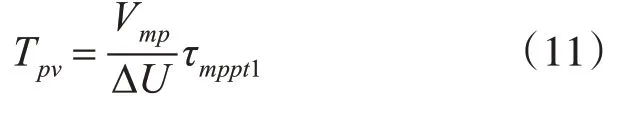
其中，Vmp为光伏组件最大功率工作点，τmppt1为跟踪算法循环调整周期，设固定步长为Δδpv，自适应变步长为Δψpv。根据式（11）可以推出Δδpv的大小为

根据步长与功率差值之间的关系，自适应步长Δψpv可以表示为

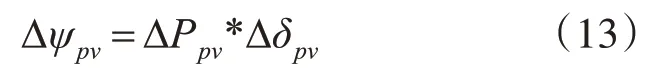
其中，ΔPpv为相邻两次寻优的相对功率变化量的绝对值，其关系式可以表示为

其中，Ppv（k）为当前输出功率，Ppv（k-1）为上一次输出功率（W）。为了量化Ppv，按功率变化量的绝对值大小与额定功率百分比来设定取值区间，设功率区间分别为εn（n=1，2，3…），区间的多少可以根据控制的精度和速度来调整。

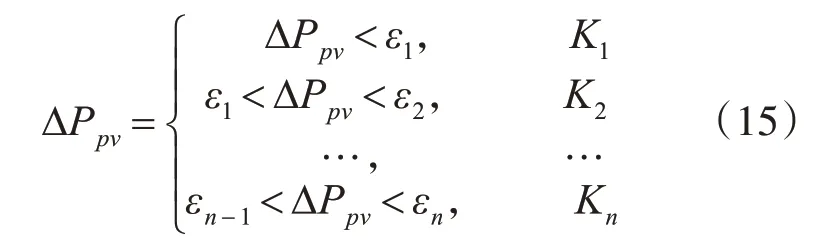
其中，K1，K2…Kn为区间系数。因此，光伏组件在k+1时刻的输出参考值为

其中，ψpv(k)为k时刻的光伏电池输出参考值；ψpv(k+1)为（k+1）时刻的输出参考值，Sig为扰动方向及大小由式（17）和式（18）决定：

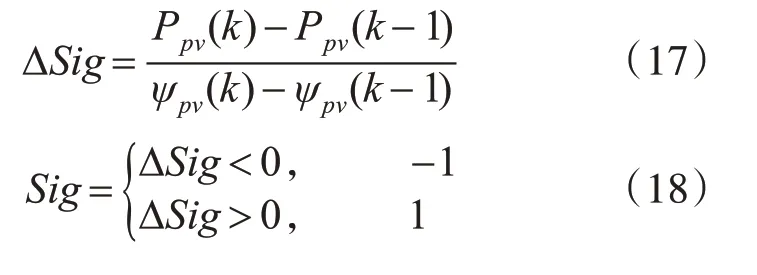
4 仿真及实验验证

为了验证本文所提方法的正确性，在Matlab/Simulink平台中构建了仿真平台如图2所示，采用Solare msx-60型光伏组件，在测试温度为25℃光强为1000W/m2时，组件的开路电压为21.1V，短路电流为3.8A，最大功率点电压为17.1V，输出最大功率为60W。采用相对和绝对误差方法来量化分析算法的实际效果如式（19）和式（20）：

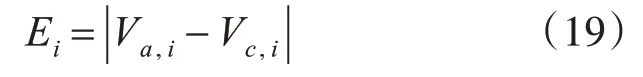
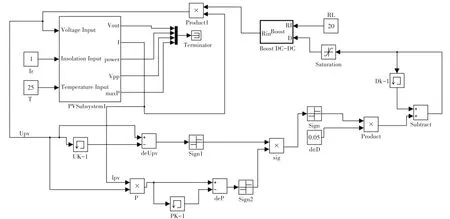
图2 Matlab/Simulink构建仿真模型

其中，i为采样点数，Ei为绝对误差值，Va，i为真实值，Vc，i为理论计算值，AEi为相对误差值。

图3给出了功率差值与步长和时间的关系。在整个跟踪过程，采用0.02步长的功率差值均小于0.05步长下的数值。而采用动态跟踪算法时，当时间小于0.006s时，功率差值等于0.05步长下的值；在［0.006s，0.025s］区间内自适应到以0.02步长跟踪，并且自适应算法的功率差值小于以0.02为步长的小步长扰动。在0.025s之后与小步长功率差值相同。通过对图3对比分析可得，动态跟踪方法可以加快减小功率震荡，提高跟踪精度、具有良好的收敛性。

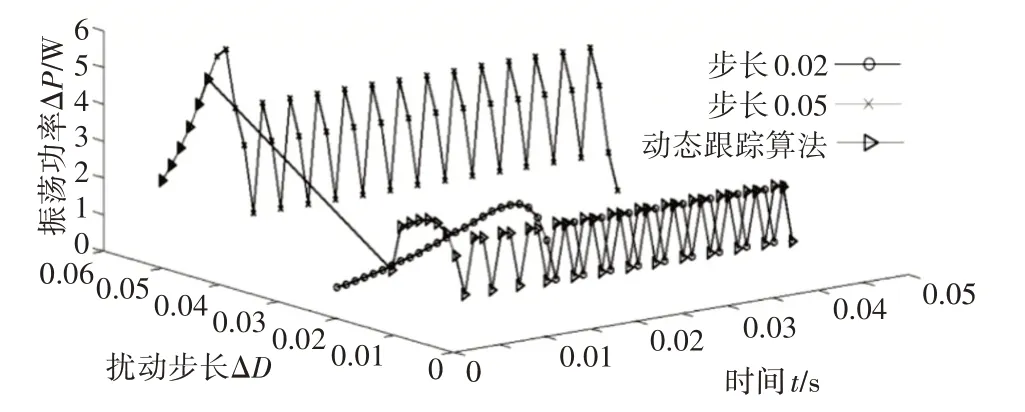
图3 功率差值与步长和时间之间的关系

表1给出了不同算法下的对比结果，从跟踪时间来看，分别为0.025s、0.009s和0.006s。在相同的扰动功率下，动态跟踪算法的跟踪时间比0.02步长下提高了2.8倍。从稳态扰动功率来看，0.02步长下的相对误差为2.6%，0.05步长下的相对绝误差为6.7%和动态跟踪算法的相对误差为2.6%。在相同的跟踪时间下，动态跟踪算法的相对误差比0.05步长下提高了4.1%。从获得的最大功率来看，0.02步长与动态跟踪算法的最大功率相同，和测试真实最大功率点相差0.8%。0.05步长下的最大输出功率和测试真实最大功率相差4.9%。总结图3和表1可得，动态跟踪算法在相同的跟踪精度下，跟踪时间相比0.02步长下提高了2.8倍；在相同的跟踪时间下，功率偏差相对误差比0.05步长下提高了4.1%。

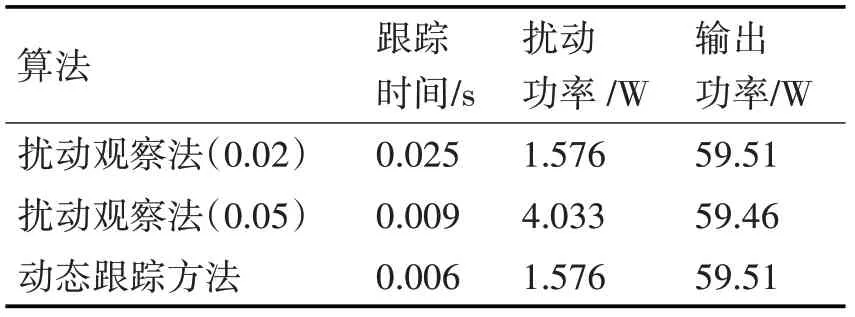
表1 不同算法下的结果对比

图4为载体运动时光伏组件输出功率。从图4可以看出，当载体运动时，光照强度从700W/m2变化到800W/m2，光伏组件最大输出功率快速从42.1W变化到48.3W，输出占空比稳定，输出功率响应快，调整时间短，实现了载体运动下光伏组件最大功率点的动态跟踪。

图4 载体运动时光伏组件输出功率

5 结语

本文针对载体运动状态下光伏组件最大功率点跟踪控制问题，提出了一种快速动态跟踪方法。仿真及实验验证了方法的有效性，结果表明，该方法具有跟踪速度快、效率高的优点。相比常规的扰动观察法，输出功率提高了4.1%。