融合差异进化的混合算法求解多选择背包问题*

蒋 妍 潘大志

（西华师范大学数学与信息学院 南充 637009）

1 引言

多选择背包问题（Multiple-choice knapsack problem，MCKP）是运筹学中的一个经典的NP-hard问题，由于问题自身具有配套属性，被广泛地应用于对组件串联选取［1］、资本预算和菜单规划［2］、广义分配问题［3］等实际问题中，对该问题求解方法的研究无论在理论上还是实践中都具有一定的意义。

目前，求解MCKP的算法主要分为两类：一类是精确算法，主要包括动态规划、分支定界等，该类算法可以求出问题的精确解，但随着问题规模和复杂度的增加，问题的求解难度和时间复杂度也会呈指数增长。另一类则是启发式算法，例如狼群算法、蜂群算法、蝙蝠算法、粒子群算法、差异演化算法［4～8］等，该类算法的求解速度快，但往往仅能求出问题的次优解。

近年来，国内外学者在求解MCKP问题时，采用了很多的创新和改进方式［4～16］来提升解的质量。例如，Bednarczuk［4］借助于闭式公式，提出了一种近似解的方法，其精度与贪婪算法和精确算法的精度相当，并且可以找到原始背包问题的相应近似解；Adouani［5］等提出将可变邻域搜索（VNS）与整数规划（IP）有效地结合起来，解决了带设置的多项选择背包问题；Balashov［6］提出了一种求解该问题的分枝定界算法，以及一种提高算法性能的上估计计算和优化方案；杨洋［7］基于凸帕累托算法（CPA），提出一种能够快速求解线性支配子集的改进帕累托算法，大大提升了求解的速度和精度；谭阳［8］构建了待选物品价值权重因子，平衡了极值效应对算法寻优过程的影响，同时采用新的修复机制，进而有效地优化MMKP问题；董亚科［9］等设计了基于离散空间的狼群算法，给狼群设计了新的游走、奔袭、围捕方式，进而提高了算法的求解精度；吴迪［10］等通过设置两个自适应变化的雄蜂群和雌蜂群，差分进化，有效地平衡了算法的全局搜索与局部搜索，进而避免算法陷入局部最优；李枝勇［11］等提出了一种改进的蝙蝠算法，引入了惯性因子，并重新定义了蝙蝠的速度的更新方程，有效地将蝙蝠算法应用于求解多选择背包问题，拓展了蝙蝠算法的应用领域；陈娟［12］等设计了一种离散粒子群优化算法对问题进行求解，通过仿真试验证明了算法的可行性和有效性；王研［13］等针对多选择背包问题的离散性设计了离散的差异演化算法，有效的解决了问题等。

为进一步提高求解MCKP问题的精度和效率，本文提出了一种融合差异进化的混合算法求解MCKP问题。算法将个体分为三个阶级，每个阶级对应特定的进化方法；同时设计了随机贪心修复策略，用于解的修复和优化。

2 多选择背包问题

有一个最大载重量为W的背包和一批具有物资消耗和重量的物品，现将物品分为m类，相互排斥，每一类含有ni(i=1，2，…，m)个不同的物品。多选择问题可描述为在满足背包载重的情况下，从每一类中选出一个物品，使得消耗之和最小。多选择背包问题作为背包问题的一个推广，与之不同之处在于，多选择背包增加了一个约束条件，并且将极大值问题变为了极小值问题。多选择背包问题用数学模型描述为

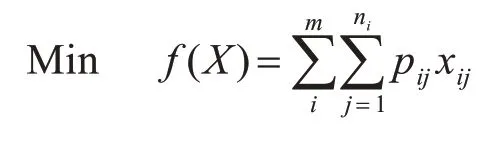
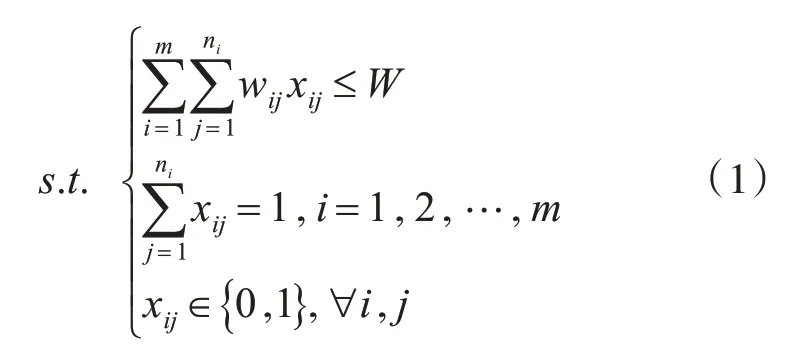
式中，f(X)为所有选入背包的物品的总消耗；pij为第i类中第j个物品的物资消耗量；wij为第i类中第j个物品的重量；X={x11，x12，…，x1n1，x21，…，xm1，…，xmnm}为决策变量，其中xij=1时表示第i类中第j个物品被选择，xij=0时表示不被选择。

目标函数为总消耗量最小；约束条件第一个为总重量不得超过背包容量；第二个为每一类选且只选一个物品；第三个为决策变量必须为0，1变量。

3 融合差异进化的混合算法

3.1 正整数编码

结合多选择背包独有的将物品进行分类的特点，本文摒弃了背包问题常用的二进制编码方式，采用了更为适合的正整数编码。以物品的类别数m作为解的维度，每一维以[1，ni](i=1，2，…，m)作为范围，选取任意正整数，作为该类的选取方案。用数学公式表示为

3.2 阶级划分

在算法中，依照适应度值，按一定的比例将种群分为三个阶级，依次定义为底层阶级、中层阶级和高层阶级三类。阶级划分算子的具体步骤如下。

算法1：阶级划分算子

步骤1：设置三个空集合L、M、U，分别记录底层阶级、中层阶级和高层阶级的个体；

步骤2：将所有个体按照适应度值进行降序排列，并将第k个个体对应的排名记为ind exk；

步骤3：若indexk≤m1*N P，则第k个个体被放入集合L中；若m1*N P＜indexk≤m2*NP，则放入集合M中；若ind exk＞m2*N P，则放入集合U中。

3.3 个体差异进化

3.3.1 底层阶级

当个体处于底层时，往往很难有大的提升，反而可能往错误的方向移动。因此应该放弃当前位置，向全局最优学习或重新初始化位置。基于此，对于底层阶级的个体，设置了重启策略，按照物品的类别依次进行，促使其往好的方向移动。重启算子的具体操作如下：

算法2：重启算子

步骤1：生成一个随机数rand，并与概率参数P进行比较；

步骤2：若rand＜P则学习全局最优个体，若rand≥P则重新生成初始个体，即：

步骤3：重复步骤1～2，直至每一维都更新完毕。

3.3.2 中层阶级

对于中层阶级的个体而言，可以从个体和社会的经验中进行学习。基于此，针对中层阶级的个体，本文融合了遗传算法和鱼群算法的思想，设计了自我学习和社会学习两个算子。

1）自我学习

自我学习融入了遗传算法的思想，将当前个体与历史最优进行交叉，通过向自身经验学习来进行更新。自我学习算子的具体操作如下。

算法3：自我学习算子

步骤1：在[1，m]间选取两个随机整数k1，k2(k1≠k2)，确定为交叉位置；

步骤2：用历史最优个体中k1到k2维的基因段替换当前个体中k1到k2维的基因段。得到新个体

2）社会学习

社会学习融入了人工鱼群算法的思想，先给个体设定一个可视范围，并计算出可视范围内所有个体的重心和最优值，再通过交叉的方式分别向重心和局部最优个体学习，实现更新。以第k个个体为例，社会学习算子的具体操作如下。

算法4：社会学习算子

步骤1：设置个体的可视范围vision；

3.3.3 高层阶级

当个体处于高层时，若变动太大可能会导致直接越过最优值，因此局部搜索更有利。基于此，针对高层阶级，本文设置了扰动算子，进行小范围搜索。扰动算子的具体操作如下。

算法5：扰动算子

3.4 精英库

鉴于优个体周围出现优个体的可能性很大，因此本文设置了一个精英库，用于存储第3.3.3节中未被选中的个体。在各个子群均更新完毕后，依次将精英库中个体与种群的最差个体进行比较，择优放入种群中。

3.5 随机贪心修复策略

对于不可行解，无论其总价值有多大，都是无用的，还会让搜索停滞不前。因此，对不可行解的修复，是求解多选择背包问题的关键。鉴于多选择背包每类选且只选一个物品的特殊约束，本文设计了随机贪心修复策略，随机保证了修复后解的多样性，贪心保证了修复后解的质量。策略按照维度依次修复，以第k个个体为例，算子的具体操作如下：

算法6：随机贪心修复算子

步骤1：随机选取一个维度j，记录对应的

步骤2：找出j类中所有重量比小的物品，放入集合A中；

步骤3：若A不为空集，则进行贪心操作，找出A中物资消耗最小的物品，替换；反之，则重复步骤1～2；

步骤4：检查替换后的新个体的总重量是否满足背包载重要求，若满足则修复完成，若不满足则重复步骤1～3直至重量满足要求为止。

操作中每个维度最多被选取一次，不会出现重复选取的情况。

3.6 算法步骤

融合差异进化的混合算法的具体步骤如下。

步骤1：参数初始化。设定最大迭代次数N I，种群规模N P，可视范围vision；

步骤2：种群初始化。按照3.1所提及的正整数编码方式，生成初始种群；

步骤3：生成子群。按照算法1，进行阶级划分；

步骤4：个体差异进化。对于不同的阶级，分别按照算法2～5进行更新，并更新精英库；

步骤5：解的修复。按照算法6，对不可行解进行修复；

步骤6：贪心装载。依次将精英库中的个体与种群的最差个体进行比较，择优纳入种群；

步骤7：重复步骤3～步骤6，直到达到最大迭代次数NI。

算法的流程图如图1所示。

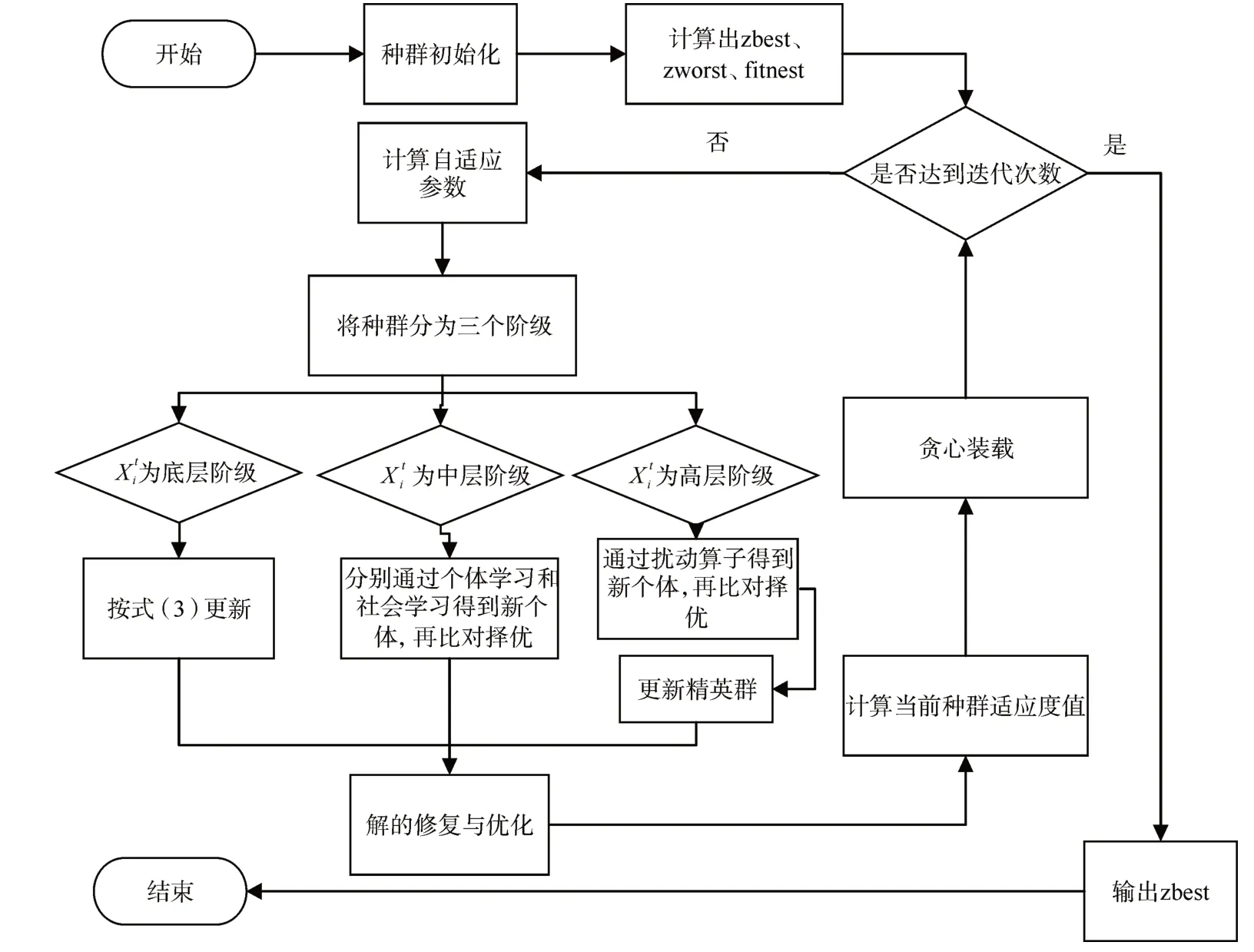
图1 算法流程图

4 仿真结果分析

4.1 测试算例

为测试融合差异进化的混合算法求解多选择背包问题的有效性，本文采用文献［4］提出的一个含有八类物品的经典多选择背包实例来进行仿真实验，问题实例具体如下。

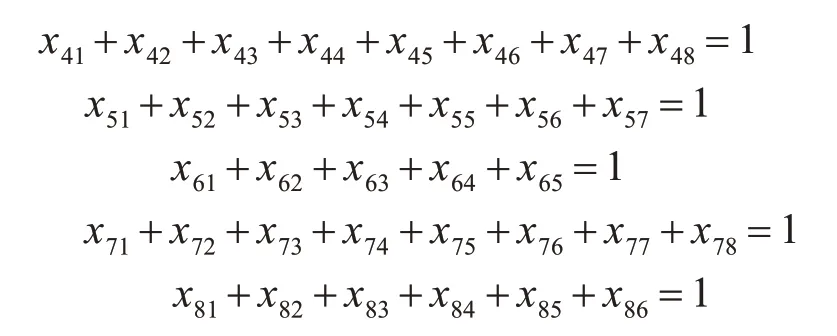
算例的理论最优值为34。

4.2 参数设定

4.2.1 通用参数

种群规模N P越大，算法得到最优值的可能性越大，但当NP达到一定值时，算法将停滞，反而会浪费很多的运算时间。在本文中，统一设定NP=40。

4.2.2 智能算法非通用参数

为验证融合差异进化的混合算法的性能，本文选取了近年来改进效果较好的两个算法：离散狼群算法［4］（DWPA）、改进的蜂群遗传算法［5］（BSGA）以及一个基本算法：基本粒子群算法（PSO）与本文算法进行比较，每个算法的非通用参数设置如表1。

表1 智能算法非通用参数设置

4.3 算法对比

为融合差异进化的混合算法的性能，本文运用选取的算例对IDEHA进行测试，并将结果上述的DWPA、BSGA以及PSO进行比较。算法均在处理器为Intel（R）Core（TM）i5-6200U CPU@2.30GHz 2.40 GHz，内存为8GB，操作系统Windows 10的计算机上使用Matlab 2016b进行仿真实验。实验中每个算法均独立运行100次取得平均值，实验结果如表2及图2所示。

由表2分析可得：

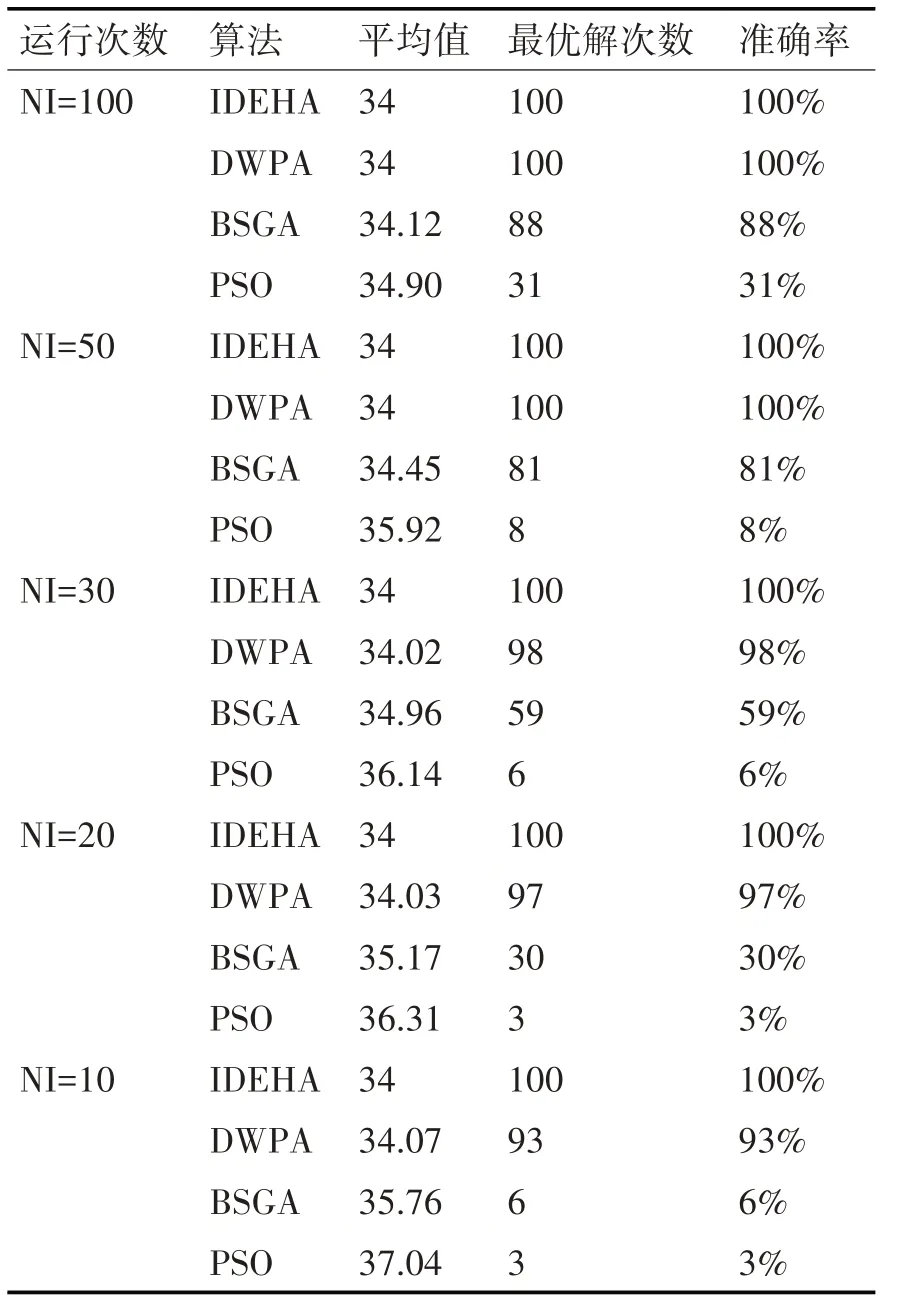
表2 智能进化算法求解典型测试算例性能分析

1）当NI=100、NI=50时，迭代次数较大，算法IDEHA和DWPA能够求得完全最优解，但算法BSGA和PSO不能，说明算法BSGA和PSO存在陷入局部最优的情况。表明算法IDEHA和DWPA的寻优能力相较之下更强。

2）当NI=30、NI=20、NI=10时，随着迭代次数的减小，算法IDEHA依旧维持着最优解和100%的准确率，而算法DWPA出现了不能完全求得最优解的情况，算法BSGA和PSO的平均值和准确率也进一步变差，表明算法IDEHA的收敛速度相较之下更快、稳定性更强。

总体看来，算法IDEHA无论是在寻优能力还是稳定性、收敛速度，都优于其他算法。

下面展示算法的迭代对比图，如图2所示。

图2 测试算例优化求解收敛图

由图2分析可得：算法IDEHA的迭代起始点普遍低于其他算法，曲线的下降幅度更明显，最早到达最低点，表明算法的收敛行强，收敛速度快；其次，算法IDEHA的迭代终止点普遍低于其他算法，表明算法的寻优能力强。

综合以上的仿真实验结果、迭代图及分析，可得DEAIEF算法寻优能力强、求解精度高、稳定性和鲁棒性强、收敛速度快，适合求解MCKP问题。

5 结语

本文提出了求解多选择背包问题的融合差异进化的混合算法，算法通过差分进化提高算法的动态适应性；提出了随机贪心修复策略来修复和优化解；引入精英库加快算法的收敛速度。并通过经典的多选择背包算例进行仿真实验，对比了近期提出的其他优秀的启发式算法（离散狼群算法、改进的蜂群遗传算法）以及基本算法（基本粒子群算法），实验表明本文算法具有较好的寻优能力、稳定性、收敛性，是一种更为有效的求解多选择背包问题的算法。