基于壳-弹簧模型的预制地下管廊横向抗震分析
甘梦云,梁建文,李东桥,赵 华
(1.天津大学建筑工程学院,天津 300350;2.天津市建筑设计院,天津 300074)
引言
地下综合管廊分为整体现浇式和预制装配式两种。预制装配式管廊由于预制接头的存在弱化了结构的整体刚度,因此预制接头成为地震作用下的薄弱环节。目前,已有研究通过壳模型分析预制接头对综合管廊纵向抗震性能的影响[1],而在横向抗震分析方面,研究大多仍将预制管廊看作平面问题考虑,采用二维梁模型模拟管廊结构,忽略纵向接头构造及初始装配预应力等因素对其横向抗震性能的影响,因此有必要进一步完善,为预制装配式管廊抗震设计提供参考。
目前地下结构横向抗震分析多采用反应位移法[2-3],将地震作用下的地层周围剪应力、结构自身惯性力等地震等效荷载施加于结构,并通过将土层位移差赋予地基弹簧非结构端的形式表征土-结构相互作用,进而求解结构的地震响应,但因传统方法多采用二维梁-弹簧计算模型求解,难以考虑纵向接头形式及接头预应力的影响。对于双舱等非对称截面形式的预制管廊,受接头预应力影响,地震作用下预制管廊段并非平面应变状态,传统二维梁-弹簧计算模型难以反映装配式接头及接头预应力作用,以及地震作用下管段的真实应力分布。采用壳模型可能更真实地反映在地震作用下的结构响应,已有研究将壳模型应用于大口径管道抗震分析[4]及盾构隧道的抗震分析[5-7]和地下管廊的抗震分析[8]。由于地下管廊多为浅埋结构,且预应力承插式接头与盾构隧道等结构常采用的拼装式螺栓接头在力学性能上有很大不同,地震作用下地下管廊的结构响应往往比盾构隧道等深埋结构更为不利[9]。
鉴于此,基于大型有限元通用软件ABAQUS,文中提出一种适用于预制管廊横向抗震分析的壳-弹簧计算模型,采用三向非线性弹簧模拟管段间纵向接头的相互作用,并考虑了钢绞线预应力作用。将精细化壳-弹簧模型与传统的梁-弹簧模型进行对比,讨论了钢绞线预应力和混凝土塑性等因素对管廊横向抗震分析的影响,相关研究结果可为预制管廊结构的抗震分析提供参考。
1 基于壳-弹簧模型的改进反应位移法
1.1 计算模型
采用壳单元模拟管廊结构,管廊周边土体模拟为支撑结构的地基弹簧,土体变形通过地基弹簧施加于结构,如图1所示。为模拟纵向接头的拉压异性力学行为,管段间采用三向非线性弹簧单元模拟承插式接头止水橡胶和混凝土协同抗压和抗剪作用,以及腋角处预应力钢绞线的抗拉作用。
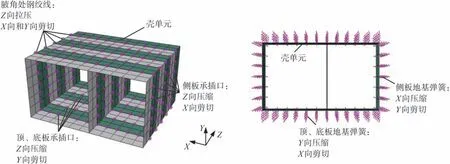
图1 壳-弹簧模型Fig.1 Shell-spring model
1.2 管廊纵向承插口接头力学行为模拟
管廊接头纵向受压时,抗压刚度由管段承插口缝隙填充的止水橡胶板及管廊混凝土共同决定。小变形下,橡胶的压缩模量较之混凝土小很多,接头间压缩变形主要由止水橡胶承担,此时弹簧刚度kZ1取接头止水橡胶垫的压缩模量;当橡胶受压变形增大至接头间混凝土接触时,此时弹簧刚度kZ2由混凝土压缩模量确定。管廊接头的力-位移关系曲线如图2所示。
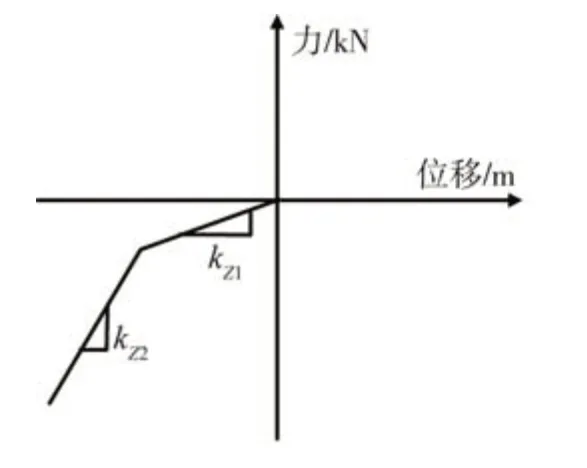
图2 承插口接头受压弹簧力-位移曲线Fig.2 Spring compressed force-displacement curve of bell and spigot joint
管廊纵向承插口接头处的受拉刚度由腋角处的预应力钢绞线承担。对于预应力的施加,以往研究[10]多通过施加恒定的装配力或建立实体钢棒来实现接头预应力的预紧效果,难以模拟接头预紧力随位移而变化的特性。因此,文中通过移动钢绞线弹簧力-位移曲线的纵坐标轴的方式达到预应力施加的效果,非线性弹簧刚度由钢绞线的屈服强度和极限强度来确定,其力-位移曲线应为一个双线性曲线如图3 所示。其中,kZ3和kZ4分别为钢绞线弹性状态刚度和屈服状态刚度。可以看到,弹簧变形为0 时管廊腋角处已受到大小为P的装配力;该弹簧受压时,钢绞线装配预应力逐渐减弱,直至位移小于钢绞线张拉距离δs后弹簧失效,这与接头受压时钢绞线的真实力学行为相同。
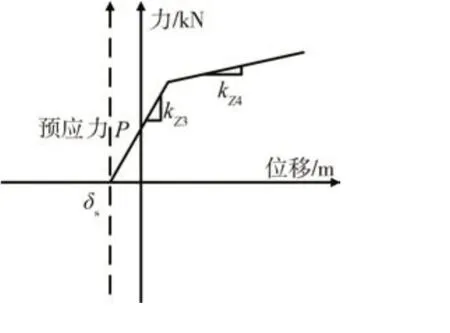
图3 预应力受拉钢绞线弹簧力-位移曲线Fig.3 Spring force-displacement curve of prestressed tension steel strand
根据承插式接头构造,考虑管廊纵向接头剪切刚度由承插口的止水橡胶和混凝土共同决定,其受剪模式如图4所示。由于橡胶和混凝土仅受压而不受拉,故当管廊纵向接头向Y正向运动时,仅顶板受剪;向Y负向运动时,仅底板受剪,因此于接头顶、底板处布置Y向拉压异性弹簧单元;同理,在侧板处布置X向拉压异性弹簧。剪切弹簧刚度kX1、kY1和kX2、kY2与承插口受压弹簧刚度kZ1和kZ2相同。
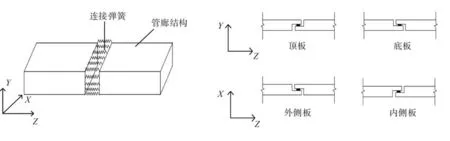
图4 承插口接头剪切弹簧方向示意图Fig.4 Diagram of shear spring direction of bell and spigot joint
1.3 地基弹簧
采用地基弹簧来模拟土-结构的相互作用,本文中地基弹簧的刚度参考日本《铁路抗震设计规范》[11]中的经验公式,如式(1)~式(4)所示:
顶、底板法向弹簧系数:

顶、底板剪切弹簧系数:

侧板法向弹簧系数:

侧板剪切弹簧系数:

式中,E0为土体动弹性模量;Bv、Bh分别为顶板宽度和侧板高度;Kv、Kh分别为顶、底板和侧板的法向弹簧系数,Kvs、Khs分别为顶、底板和侧板的剪切弹簧系数,该系数与弹簧作用面积的乘积即为法向和剪切弹簧刚度。
2 算例
2.1 工程概况
以天津市某典型深厚软土场地中的双舱预制综合管廊工程为例进行分析,管廊横向宽11 000 mm,其中大舱室宽6 100 mm,小舱室宽4 900 mm,高5 750 mm,顶板和侧板厚550 mm,底板厚600 mm,中隔板厚3 00 mm,截面尺寸如图5所示。管廊埋深3m,预制管廊节段长1.5 m,管段间由承插口相接。结构混凝土等级C60,密度2 600 kg/m3,弹性模量35.5 GPa,泊松比0.2,在腋角处配置预应力钢绞线,其张拉锚固下控制应力为1 395 MPa,预应力损失值采用简化方式,后张法取张拉控制应力的20%,计算得到有效预应力为1 116 MPa,则图3中P为156 kN。
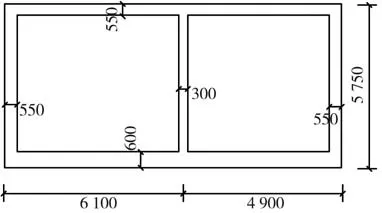
图5 双舱管廊截面Fig.5 Section of double-cabin utility tunnel
土层总厚度80 m,分为4类土层,各土层参数如表1所示。土体动力非线性曲线如图6所示。
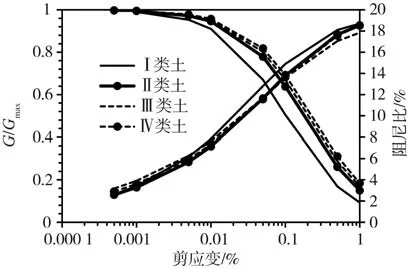
图6 土层非线性特性参数Fig.6 Nonlinear characteristic curve of soils
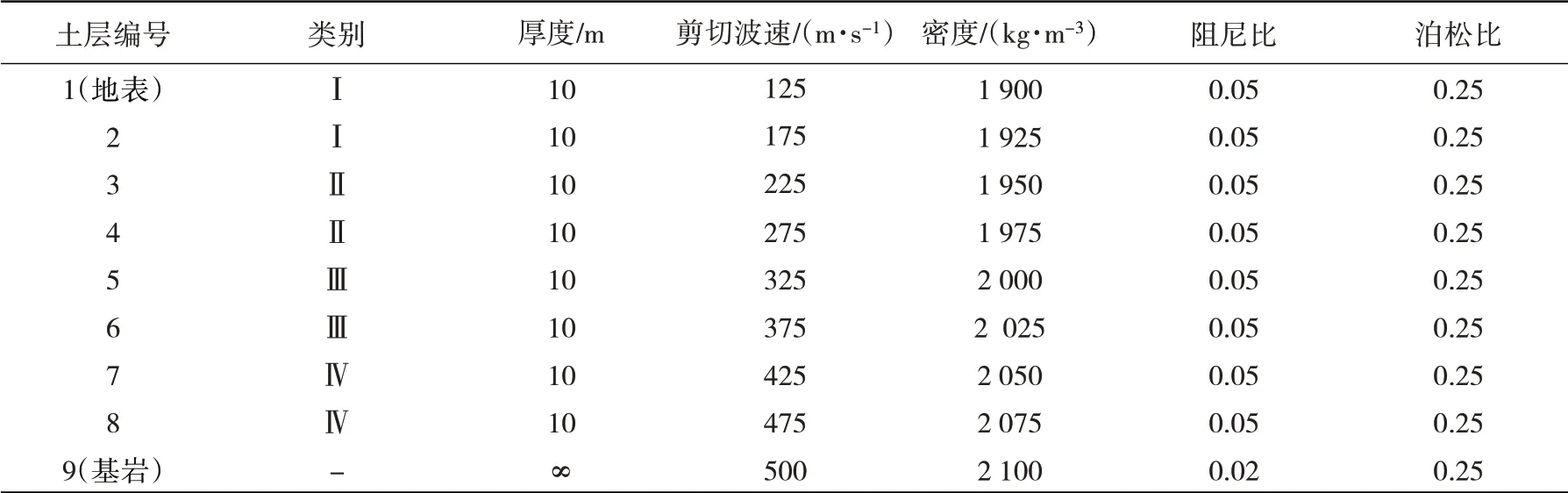
表1 土层参数Table 1 Soil parameters
选取E2(中震)及E3(大震)安评波,加速度峰值分别为0.2 g和0.38 g,如图7所示。
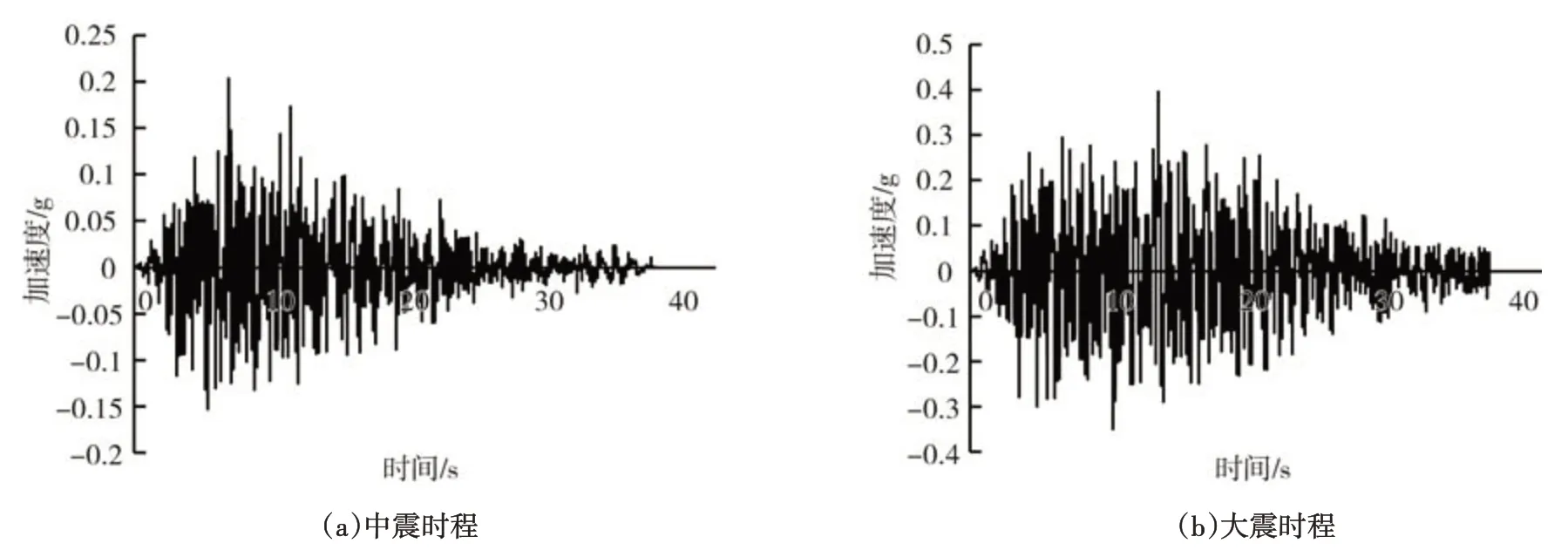
图7 安评地震波Fig.7 Safety evaluation seismic wave
2.2 计算模型及模型参数
采用壳单元模拟结构,《地下结构抗震设计标准》等[2-3]现行标准中规定,模型纵向网格尺寸Δz按预制管段长度确定,为方便布设地基弹簧,本文取为预制管段长度的1/2,即Δz=0.75 m;横向网格尺寸在场地最短地震波长的1/8~1/12的基础上,作加密处理,本文取为Δx=Δy≈1 m。预制管段间设置连接弹簧模拟接头力学行为;预制管段间连接弹簧刚度根据接头构造及混凝土、橡胶及钢绞线的材料属性计算得到[12],如表2 所示。

表2 管段间弹簧刚度取值Table 2 Spring stiffness between segments
其中,管廊接头轴向弹簧刚度系数由Kzi=EA/l取值(Kzi为轴向弹簧不同阶段的刚度系数,E为钢绞线弹性模量[13],或混凝土弹性模量[14],或橡胶弹性模量[15],A为钢绞线截面积或混凝土承压面积,l为钢绞线有效长度)。
为避免拟研究管段以外预制管段的边界约束影响且兼顾计算效率,确定计算模型尺寸。由2 个管段开始计算,逐渐增大纵向管段数,经过多次试算,当拟研究的中间管段的内力变化幅度在1%以内时,确定为计算模型的纵向尺寸。文中模型最终取为6节预制管段,纵向计算长度9 m。
管廊四周布置地基弹簧,其刚度由式(1)~式(4)计算得到。由于土体对结构只存在压力,因此法向地基弹簧无抗拉作用。同时,土体在剪切变形过程中存在屈服位移δ,当土体位移超过该屈服位移时,提供的剪力将不再增大,本算例管廊处于软黏土土层,土体屈服位移δ取0.01 m[16]。计算得到的梁-弹簧模型中顶、底板和侧板的地基弹簧刚度如表3 所示。因壳-弹簧模型中一个预制管段沿纵向划分为2 个网格,故壳-弹簧模型中地基弹簧取表3计算数值的一半。

表3 地基弹簧刚度Table 3 Foundation spring stiffness
通过一维地震分析程序EERA[17]获得自由场土层的相对位移,取模型顶、底板处土层出现最大相对位移时刻为最不利时刻,并将此时刻的结构惯性力及地层剪力施加于结构,相对位移施加于地基弹簧远端,进行横向抗震计算。
2.3 计算工况
选取了4个计算工况,如表4所示。工况1梁-弹簧模型采用B31 梁单元,无纵向连接弹簧,为将文中壳-弹簧模型与梁-弹簧模型进行对比,文中将梁单元计算深度取为1.5 m(与预制管段长度一致);工况2 的壳-弹簧模型约束纵向自由度,模型纵向接头无钢绞线预应力作用,以保证其平面问题假定,且将结构设置为与梁-弹簧模型相同的线弹性本构,用于与梁-弹簧计算模型进行对比。为研究结构塑性及纵向接头预应力对预制管廊横向抗震性能的影响,工况3计算模型于纵向接头施加钢绞线预应力;工况4施加结构塑性及损伤。
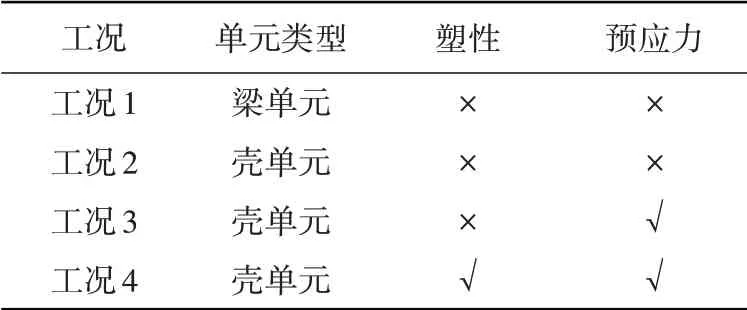
表4 各工况类型Table 4 Types of working cases
工况4 计算模型采用ABAQUS 中Rebar 功能,根据截面配筋设计将管廊顶、底板、侧板和中隔板弥散相应的钢筋。混凝土塑性损伤采用ABAQUS 中的CDP 模型,混凝土非弹性拉压应变与拉压应力、损伤因子的数据如表5所示,CDP模型中其他参数如表6所示[18]。
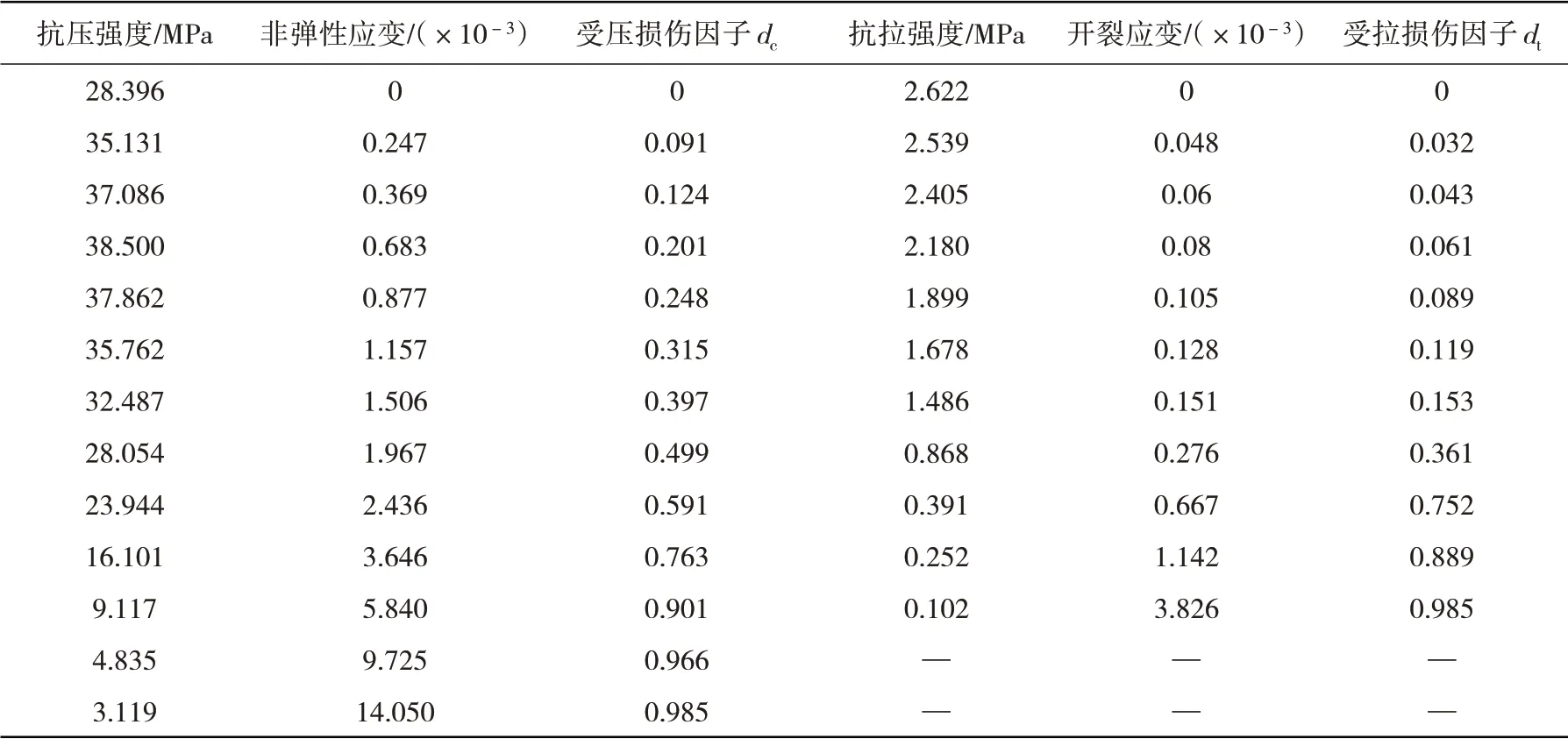
表5 混凝土材料塑性参数Table 5 Plastic parameters of concrete materials

表6 CDP模型其他参数Table 6 Other parameters of CDP model
3 结果与分析
3.1 平面应变假定下壳-弹簧模型(工况2)计算结果与梁-弹簧模型(工况1)计算结果的对比
中震作用下,线弹性壳-弹簧模型(无预应力)计算结果与梁-弹簧模型(规范方法)计算结果的对比如图8所示。其中,壳-弹簧模型的内力图取自管廊6个管段中最中间的2个管段。由于壳-弹簧模型中1个预制管段沿伸度划分为2个单元,因此其2个单元合力即为管段该处的内力。

图8 中震作用下壳-弹簧模型与梁-弹簧模型内力对比Fig.8 Comparison of internal forces between shell-spring model and beam-spring model under moderate earthquake
可以看到,两个工况内力分布相似,但壳-弹簧模型(工况2)内力略大于梁-弹簧模型(工况1)内力,其中轴力、剪力和弯矩峰值分别增大17.4%、22.7%和27.9%。这说明,相比文中考虑纵向接头的精细化壳-弹簧模型,采用现行规范方法进行预制管廊的横向抗震计算时,其结果对管廊的内力响应有所低估。
3.2 预应力钢绞线的影响(工况2和工况3对比)
中震作用下,管廊结构在有预应力(工况3)与无预应力(工况2)时的轴力云图(本文中的轴力均指沿管环方向的轴力)、剪力云图和弯矩云图如图9~图11所示。

图9 轴力云图Fig.9 Nephogram of axial force
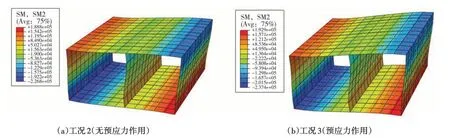
图11 弯矩云图Fig.11 Nephogram of bending moment
可以看到,工况2 无预应力的壳-弹簧模型内力沿模型纵向分布一致。受预应力作用时(工况3),对于非对称截面形式的双舱管廊,其内力分布已不再符合平面问题假定,可以看到,工况3有预应力的壳-弹簧模型中结构轴力显著增加,且其分布在幅宽(尤其是腋角钢绞线处)出现明显变化,而弯矩和剪力的变化相对较小。有预应力时轴力、剪力、弯矩峰值较无预应力时的峰值分别增加37.3%、7.2%和4.6%。因此,对于非对称截面形式的预制双舱管廊,接头钢绞线预应力存在时,如仅作平面应变问题考虑,将难以反应管廊结构的真实内力分布。
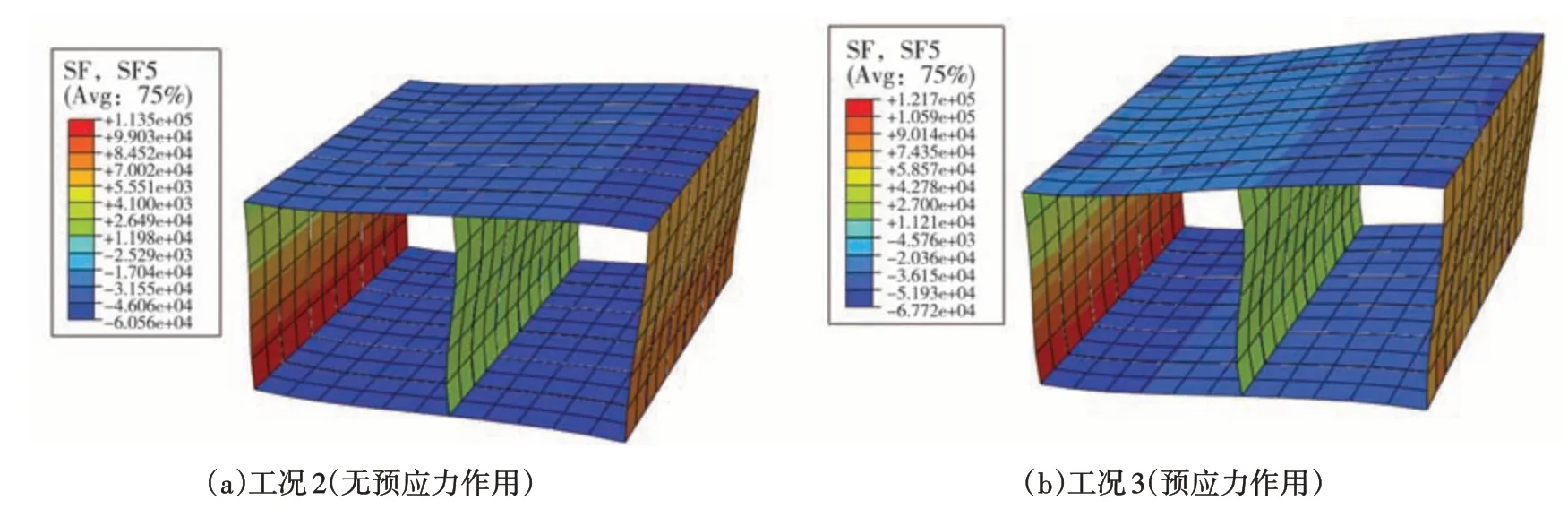
图10 剪力云图Fig.10 Nephogram of shear force
3.3 管廊结构塑性的影响
为分析管廊结构塑性对计算结果的影响,计算大震作用下,工况1、工况3和工况4模型的层间位移角,如表7所示。

表7 层间位移角Table 7 Displacement angle between top and bottom slab
可以看到,由于梁-弹簧模型中结构仅施加线弹性本构,因此无塑性时工况1与工况3层间位移相差较小;当考虑结构塑性后,工况4层间变形显著增大,变化幅值为68.4%。
考虑塑性损伤的壳-弹簧模型可以显示管廊塑性损伤部位,工况4模型在大震和中震作用下混凝土损伤云图如图12所示。
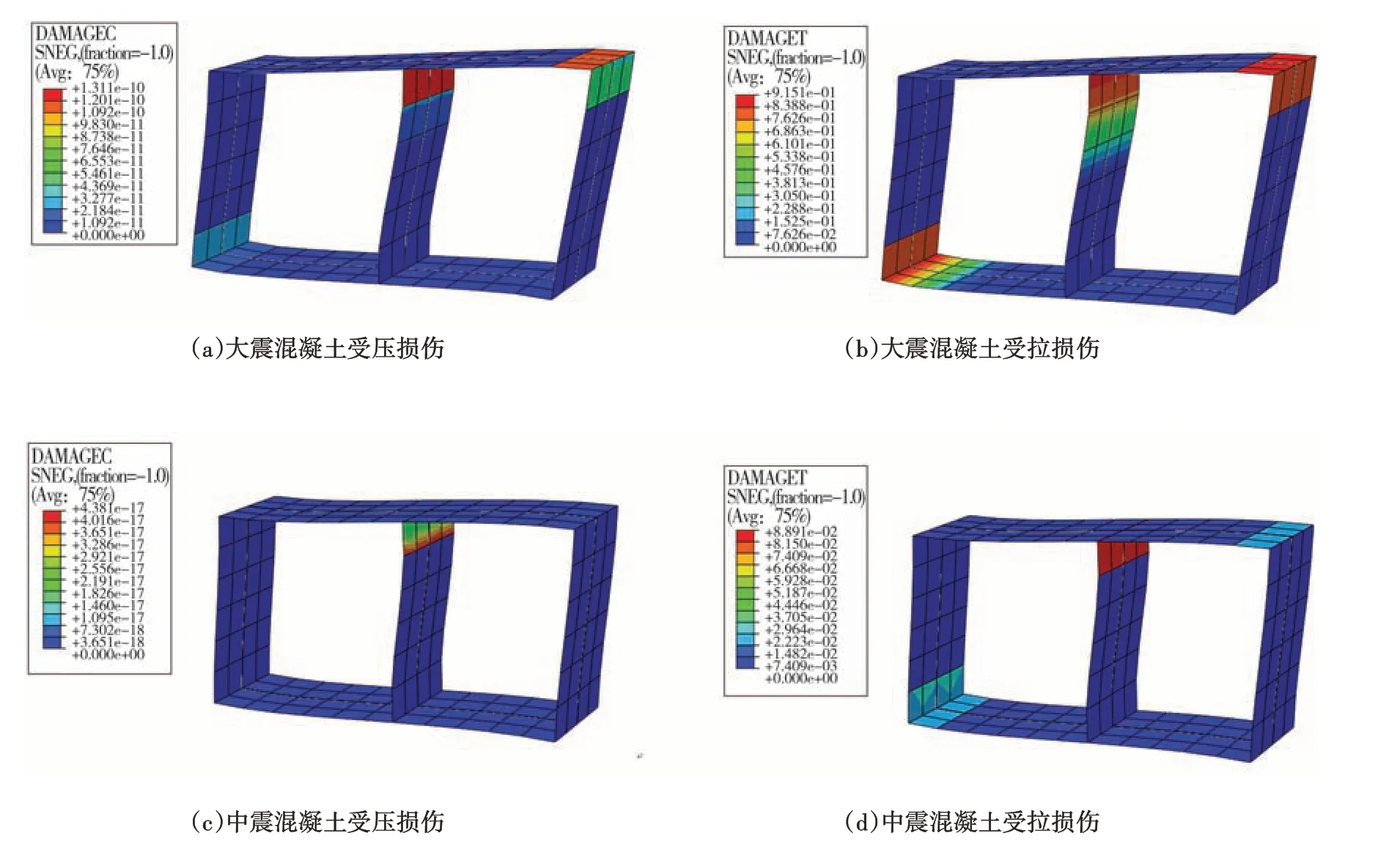
图12 工况4在大震和中震作用下混凝土损伤Fig.12 Concrete damage under large and moderate earthquakes in Case 4
可以看到,横向抗震分析中管廊结构主要受剪切变形作用,大震和中震作用下混凝土受压损伤较小,而对于受拉损伤,在大震作用下最大值为0.915 1,在中震作用下最大值为0.088 9。当混凝土抗拉强度下降至接近峰值的50%时,结构发生受拉破坏。根据表5,可以看到文中管廊结构的损伤限值为0.153。显然,大震作用下,结构已超出受拉损伤限值,发生受拉破坏;而在中震作用下,混凝土尚未破坏。
另外,值得注意的是,混凝土受拉损伤严重的区域均在中隔板顶端,因此应该考虑加厚中隔板厚度来抑制混凝土在地震作用下的损伤。
4 结论
文中提出一种考虑接头钢绞线预应力作用的壳-弹簧计算模型,以天津市某拟建地下综合管廊为例,进行了横向抗震分析,讨论了混凝土塑性和管廊的装配预应力对管廊横向抗震分析的影响,并得到以下结论。
(1)相较现行规范中建议的梁-弹簧模型(未考虑纵向接头),考虑纵向接头的精细化壳-弹簧模型计算得到的内力偏大,轴力、剪力和弯矩峰值分别增大17.4%、22.7%和27.9%,说明现行规范在处理预制管廊横向分析时,对管廊的内力可能有所低估。
(2)对于双舱等非对称截面形式的预制管廊,受接头预应力作用时,其受力状态不再满足平面应变假定,导致管廊内力分布在幅宽上有明显变化。其中,轴力变化较为显著,轴力峰值较无预应力时增加了37.3%;剪力和弯矩变化较小,剪力和弯矩峰值分别增加7.2%和4.6%。
(3)文中壳-弹簧计算模型可以考虑纵向接头及接头预应力作用,其力学性能更接近真实工况。同时,当考虑管廊结构塑性时,结构层间变形显著增大,层间位移角较梁-弹簧模型增大68.4%,模型以受拉损伤为主,主要出现于腋角钢绞线处及中隔板顶部,建议增强该处配筋。
综上,考虑纵向接头及预应力作用的精细化壳-弹簧模型可以更全面、准确地反映预制地下综合管廊弹塑性结构的受力状态,本文相关建模及计算方法对预制综合管廊抗震设计有一定指导作用。

