10-290K环境下聚酰亚胺纤维导热性能研究*
朱珊珊,林 欢,张 满,董 华
(青岛理工大学 环境与市政工程学院,山东 青岛 266033)
0 引 言
自人工合成的高分子化合物问世以来,高分子材料经历了突飞猛进的发展,目前已经成为世界上发展最迅速的产业之一[1],在生活日杂、电子电器[2]、航空航天[3]、能源[4]等领域都得到了广泛的应用,高分子科学具有极为广阔的开发新材料的背景。在众多高分子材料中,聚酰亚胺(PI)作为综合性能最佳的有机高分子材料之一,可在-200~300 ℃范围内长期使用,且部分无明显熔点,具有极好的绝缘性,103赫下介电常数为4.0,介电损耗极小,被列为“21世纪最有希望的工程塑料”之一[5]。现如今聚酰亚胺纤维在军用市场和民用市场均发展迅速,在发电技术、防护工作、节能环保和航空航天等领域都表现出优异的综合性能,这也是近年来被广泛研究的原因之一。
目前对聚酰亚胺纤维的研究主要集中在聚酰亚胺纤维及其复合材料的制备和性能上,许庆明等[6]以耐高温聚酰亚胺为基体,高硅氧纤维为增强体,制备了高温耐热树脂复合材料,并研究了树脂基复合材料的耐热性能和各组分不同配比的影响。L. Qiu等[7]提出了一种改进的线形3ω法,利用沿纤维轴向沉积的铂层加热器/温度计来测量单个多孔聚酰亚胺纤维的热导率。
本实验将研究在10~290 K温度范围内聚酰亚胺纤维的导热性,其研究结果可以为低温下的轻薄保温材料的研制提供理论帮助,用于制造野外极端天气条件下的保温毯。也可以利用聚酰亚胺纤维的导热性能来制造温湿度要求十分严格的IDC机房制冷保温材料,利用这种性质,可以减少通过制冷以达到温湿度标准的碳排放,以达到环保节能的目的。
1 实验材料
应用于本次实验的样品是由长春高琦聚酰亚胺材料有限公司提供的聚酰亚胺纤维,型号为轶纶95,对聚酰亚胺纤维进行SEM测试,如图1所示;对样品进行拉伸性能测试试验可得到样品的技术参数:断裂强度>4.0 cN/dtex、断裂伸长度>20 %、干热收缩率(280 ℃ 30 min)<0.3 %;样品1的长度和直径为571.3和15.0 μm,样品2为614.0和14.4 μm。

图1 5 000倍放大下PI纤维表面的SEM图Fig 1 SEM image of the surface of PI fiber at 5,000 times magnification
本实验主要使用到的仪器为磁控溅射镀膜仪(Q150TS,英国Quorum公司);微电流源(KEITHLEY 6221,美国Keithley仪器公司);示波器(DSO-X3052A,美国Agilent科技有限公司);数字万用表(15B+,美国Fluke公司);光学显微镜(DM270OP,德国Leica微系统有限公司)等。实验将监测在10~290 K内温度稳定时对样品通入电流的电压波动响应,会用到Janis CCS-450低温系统,包括水冷机、压缩机、温控仪、分子泵和Janis ccs-450,如图2(a)所示。
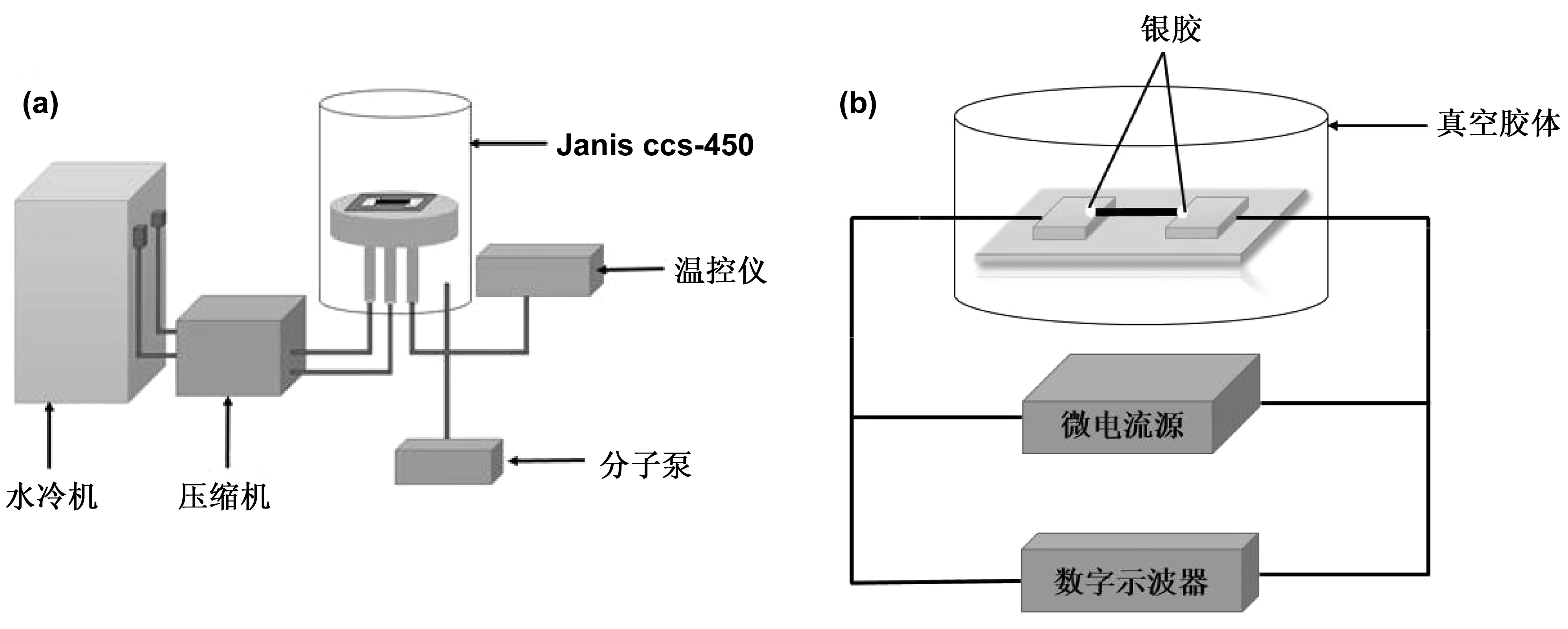
图2 实验原理图Fig 2 Experimental device diagram
2 实验方法
实验采用瞬态电热技术(transient Electrothermal technique,简称TET),TET是研究一维微尺度材料导热性能的一种技术,该技术具有测量范围广、测量周期短、测量信号强等特点,并且可以通过磁控溅射镀膜仪将绝缘材料表面镀金使其具有导电性,目前该方法的准确性已经得到了充分地证实,已经被国内外学者多次使用[8-11]。
TET实验原理图如图2(b)所示,将待测样品放置于真空腔体(真空度<2×10-4kPa)中,固定在两电极之间,待测样品、数字示波器和微电流源以并联方式连接,其中微电流源将方波脉冲直流电流通入待测样品诱导焦耳加热,待测样品的平均温度迅速上升直至达到一个稳定的状态。待测样品温升是一个瞬时过程,温度变化无法记录,当电流一定时,待测样品平均温度的变化直接影响待测样品的电阻,从而影响到待测样品两端的电压,当平均温度达到稳定状态时,待测样品两端电压也趋于平衡,所以可以用待测样品两端电压的变化表示样品平均温度的变化。数字示波器记录待测样品两端的电压随时间的变化,图3是样品2在温度为10 K、通入电流为1.095 mA时两端电压随时间变化的散点图,通过电压的变化描述平均温度的变化,从而推导出待测样品的热扩散系数,计算得出待测样品的热导率。

图3 样品两端的电压随加热时间的变化Fig 3 Voltage at both ends of the sample varies with heating time
实验将在真空度<2×10-4kPa的真空腔体中进行,因此可忽略对流换热对实验结果的影响,在实验中,样品的长度远远大于其直径,可将样品中的能量传递看作沿长度方向上的一维导热,控制方程为:
(1)
式中k为导热系数,cp为比热容,ρ为密度。样品平均温度由格林公式积分求解[12]:
(2)
理论上,样品的无量纲归一化温升T*可以表示为:
(3)
(4)
式中,V0是样品的初始电压,V1是样品的稳态电压,例如在图2中可以看出,初始电压为13.36 mV,稳态电压为13.63 mV,Vsample是示波器储存的样品两端的电压,表示为:
(5)
式中,I为通入样品的电流,R0为样品的初始电阻,η为电阻温度系数,t为时间。在本实验中,温度为290 K时通入样品1和样品2的电流分别为1.82和1.00 mA,随着温度的降低,通入的电流逐渐增大,直至10 K时分别为1.98和1.095 mA。
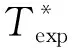
(6)
式中a1是去除辐射影响后样品的热扩散率;aeff是有效热扩散率;εr是样品有效发射率;σ是玻尔兹曼常数,取5.67×10-8W·m-2·K-4;D是样品的直径。
聚酰亚胺纤维为绝缘体,需要对材料进行镀金处理,使用真空溅射镀膜仪(Quorum Q150TS),以磁控溅射镀膜的方式在纤维表面制备厚度为20 nm的金薄膜。在本实验中,计算得到样品1和样品2的金薄膜的热扩散系数最大分别为2.29×10-7和1.92×10-7m2·s-1,已有实验证明此方法制备的金薄膜厚度的误差在10%以内[14]。去除辐射影响和金薄膜影响后样品的热扩散率可表达为:
(7)
式中areal是纤维的真实热扩散系数,L是样品的长度,R是样品的平均电阻,Aw是样品的截面积,Llorenz是金薄膜的洛伦兹数,ρ和cp是样品的密度和比热容。
联立式(6)和式(7),聚酰亚胺纤维的真实热扩散系数为:
(8)
通过在不同环境温度下进行TET实验,可以得到材料在不同温度下的比热,当样品温度稳定时,能量传递方程为:
k∂2T(x)/∂x2+q0=0
(9)
其中,q0=I2R1/AcL,R1为稳态电阻。通过求解控制方程,确定平均温升为ΔT=I2R1L/(12kAc),电阻变化反映的温度变化为ΔT=(R1-R0)/(dR/dT)其中R1-R0为焦耳加热前后的电阻变化。结合这两个方程,得到有效导热系数为:
(10)
因此比热可以由ρcp=keff/aeff表示[8],在290 K时聚酰亚胺纤维的比热容由差示扫描量热法(DSC)测量为1090 J·kg-1·K-1,体积密度为1 400 kg·m-3。
3 实验结果和分析
通过瞬态电热技术测量得到从10~290 K内18个温度的聚酰亚胺纤维的热扩散率,经计算可以得出不同温度下的比热(比热容cp与密度r的乘积)和真实热扩散系数,实验结果中各参数与温度的关系分别为图4—图6所示。
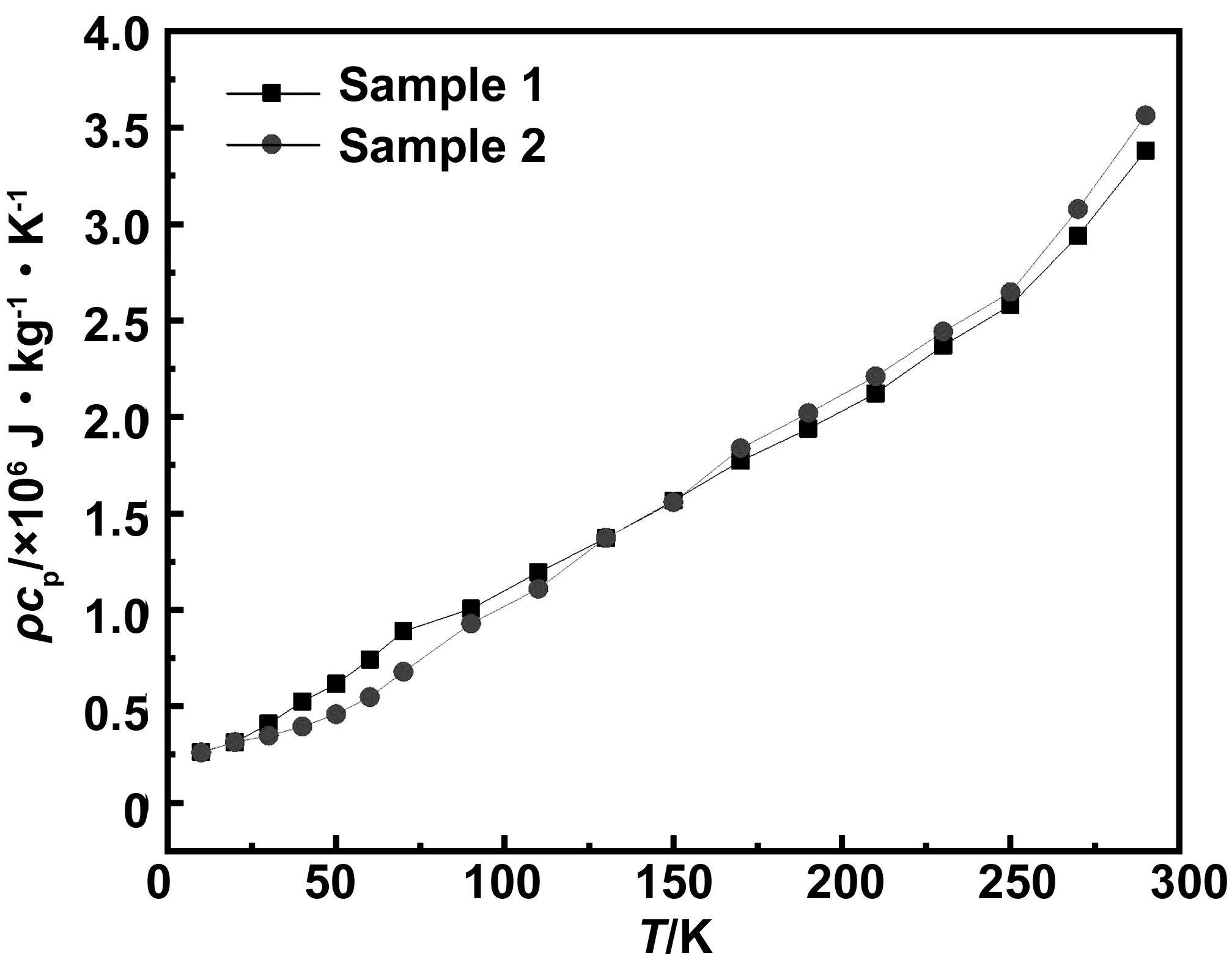
图4 比热随温度变化的关系图Fig 4 The relationship between specific heat and temperature

图5 热导率随温度变化的关系图Fig 5 Thermal conductivity as a function of temperature
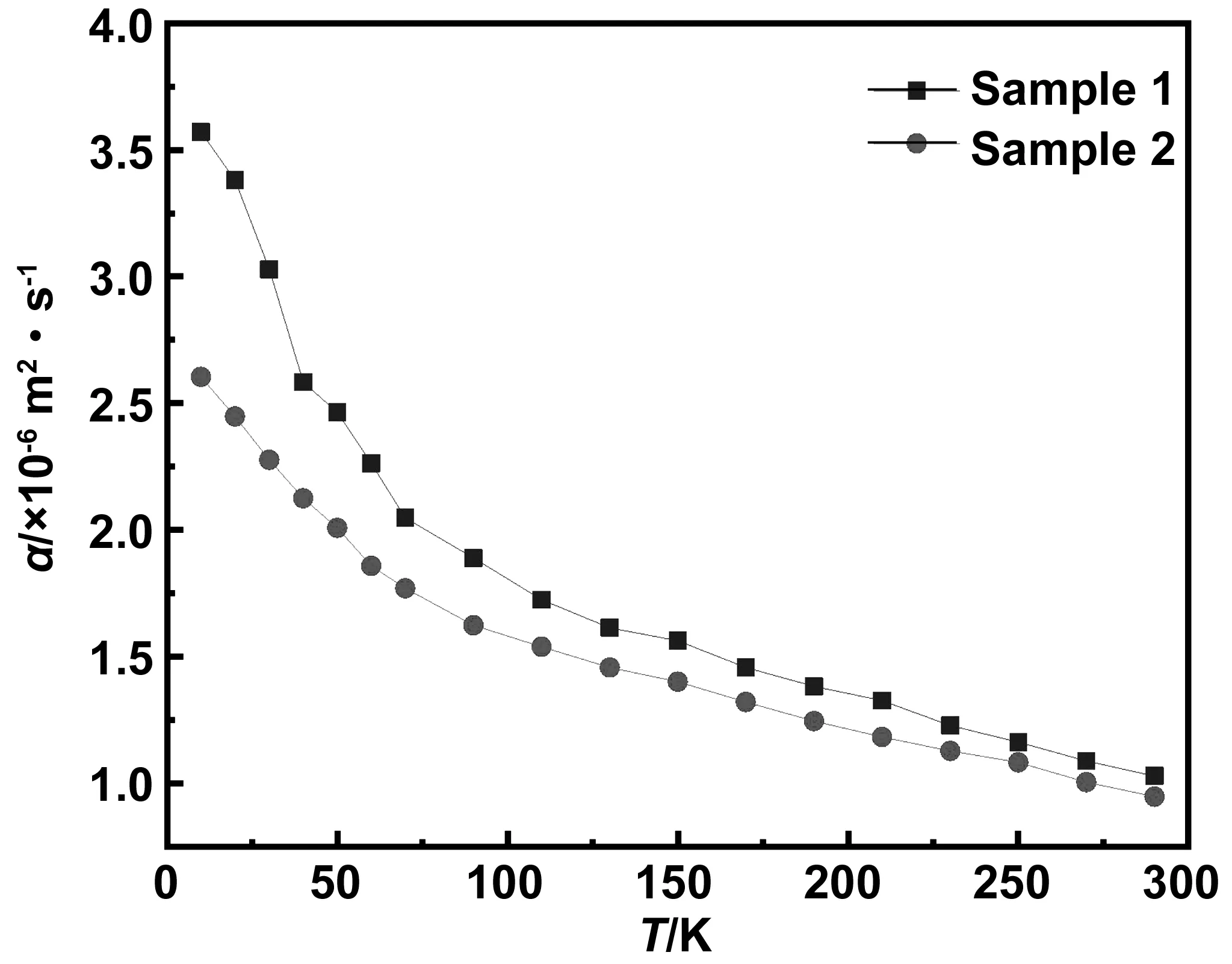
图6 热扩散率随温度变化的关系图Fig 6 The relation of thermal diffusivity with temperature
从结果得出聚酰亚胺纤维随着温度的降低,热导率和比热逐渐降低,热扩散系数逐渐升高,下面从3个方面分析该实验结果。
3.1 晶格振动对聚酰亚胺纤维热导率的影响
对于聚酰亚胺纤维这种高分子聚合物而言,内部没有自由电子,导热载体主要为声子,所以晶格振动是热传导的主要方式。聚酰亚胺纤维的热导率随温度变化的情况较为复杂:一方面聚酰亚胺纤维相对分子质量很大,分散性强,分子链无规则缠结,很难完全结晶;另一方面分子链随温度升高而振动加剧,从而对声子的散射作用也是一个重要的影响。
因晶格振动而发生热传导的固体材料,其导热性可用式(11)表示:
(11)

为了解决在低温下杜隆珀替定律热容量不为常数的缺陷,下面用德拜热容来描述热容随温度变化的关系,德拜热容的数学关系为:
(12)
其中:ξ=hw/kBT,θD=hwm/kB,θD为德拜温度,由此可以得出热容与温度的关系。
根据德拜理论,声子之间的相互碰撞和固体材料中的气孔裂纹缺陷对声子的散射以及声子平均自由程都有极其重要的影响。在德拜模型中,假定晶格为连续介质,晶格振动为连续介质的弹性波[16],平均声子数量和温度的关系为:
(13)
式中,nav是平均声子数量,wm为晶格波的振动频率,kBT为每一个简谐运动的平均能量,h是普朗克常数。德拜温度可以表示为:hωm/kB=θD,当T<θd时,n=exp(hωm/kBT);当T>θd,声子基本上被全部激发,可以粗略地表示晶格振动频率的数量级;当T≫θd时,nav=kBT/hωm,此时声子数目和温度成正比。

3.2 结晶率对聚酰亚胺纤维热导率的影响
对于非晶聚合物:在非低温区域,热导率随温度的升高缓慢增大,直至玻璃化转变温度Tg时,热导率与热容成正比;温度超过Tg后,热导率随温度升高而下降[17]。
对样品进行DMA测试如图7所示,从图中可以看出样品在400 ℃下处于弹性态区和转变区,故其玻璃化温度大于290 K。
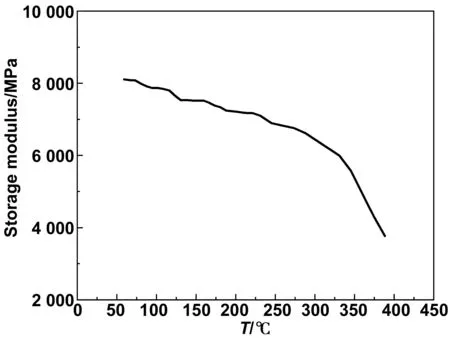
图7 聚酰亚胺纤维的DMA曲线图Fig 7 DMA curve of polyimide fiber
对于结晶聚合物:在低温区,结晶度和结晶区分子链晶型都会影响结晶聚合物的热导率,高结晶度聚合物的热导率随温度升高先增后降;伴随着结晶度的增加,极大值点向低温区偏移;低结晶度的聚合物由于非晶区占比较高且导热性差,其热导率主要由结晶区的热导率贡献,结果表现为热导率随温度升高缓慢增大,直至玻璃化转变温度出现极大值[17]。
张晓辉[18]选取PE(结晶聚合物的代表—聚乙烯)和PMMA(非结晶聚合物的代表—聚甲基丙烯酸甲酯)研究其热导率随温度的变化的规律。不同结晶率的聚乙烯随温度变化情况结果如图8所示。

图8 不同结晶率的聚乙烯(PE)的热导率随温度变化关系图[14]Fig 8 Relationship between thermal conductivity of polyethylene (PE) with different crystallization rates and temperature [14]
根据实验结果,结晶率高的PE的热导率高于结晶率低的PE的热导率,并且随着结晶率的升高,材料热导率的极大值点向左偏移。在对PMMA的研究中,热导率随温度变化的关系如图9所示。
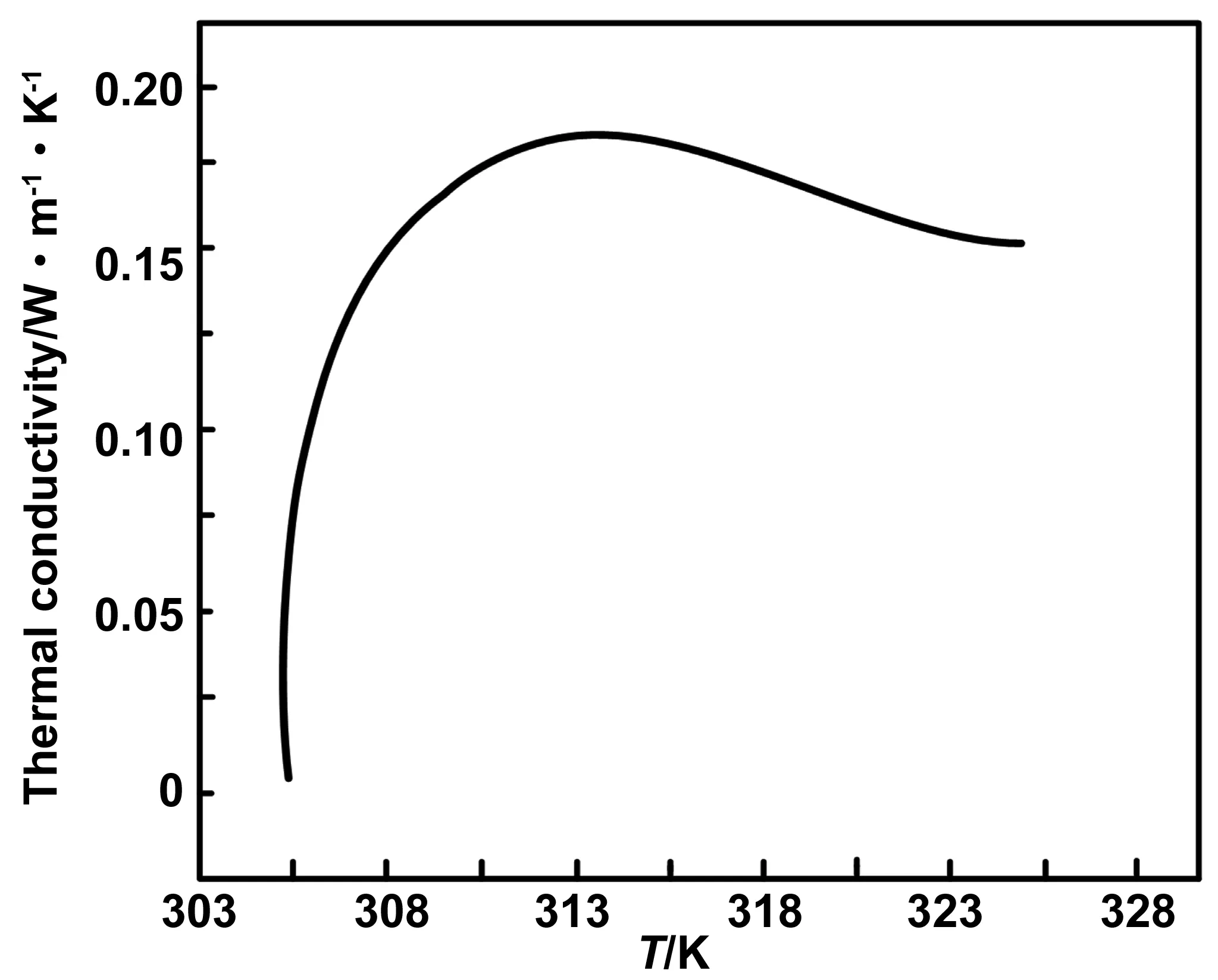
图9 PMMA的热导率与温度的关系图[15]Fig 9 Relationship between thermal conductivity of PMMA and temperature[15]
PMMA的热导率小于结晶聚合物,在玻璃化转变温度以下随着温度的升高而单调上升。高分子材料的结晶度在定向拉伸时会发生剧烈变化,原因是分子链段、晶片和晶带等沿分子链方向择优排列。已经有研究结果表明:取向程度越高的高分子材料结晶率越高[19]。而聚合物的结晶度对热导率及热导率随温度变化规律有很大的影响。下面将从结晶区和非晶区分子链结构的角度来分析其原因:晶区内分子链为有序排列,非晶区内分子链无序排列,故在晶区内声子之间碰撞较少,平均自由程较大,热导率较高,所以晶区的热导率比非晶区大。
对于本实验所用到的聚酰亚胺纤维属于半结晶聚合物,结晶率跟加工工艺有关,在对聚酰亚胺纤维加工热拉伸处理环节,聚酰亚胺材料的无定形区以及结晶区域都会沿纤维轴向进行取向,而加工的工艺影响了结晶度的高低和分子链的取向程度,从而影响了热导率随温度变化的程度和极大值点的偏移。结晶度与分子链取向之间可以相互影响,且都对高分子材料的导热性能有影响。
聚酰亚胺纤维的热导率k可由下式给出:
1/k=X/kc+(1-X)/ka
(14)
式中,C为结晶度,kc为结晶区的热导率,ka为非结晶区的热导率,且ka 根据实验数据及上述分析可以得出下面结论:在微观尺度上,聚酰亚胺纤维的热导率及热扩散率随温度的变化主要和结晶率有关。而本实验使用的材料由于其结晶率较低,热导率随温度变化的表现更接近非晶聚合物。随着温度升高,聚酰亚胺纤维的体积受热膨胀,分子的振幅变大、键长变长,分子原有体积增加,声子受到散射严重干扰并抵消了受温度升高而产生的晶格振动带来的热导率贡献。 不同的聚酰亚胺纤维制造工艺造成的缺陷可能影响热导率随温度的变化率。例如干纺工艺中初生纤维内部会残留DMAc溶剂,在该工艺高温处理过程中,DMAc溶剂的挥发会导致纤维内部留下微孔缺陷。此时材料的导热则是由材料实体本身和微孔缺陷内的空气两部分导热传递综合作用的结果。如果空气孔洞太大,那么孔洞内的对流换热和辐射换热也不可忽略,尤其是当温度升高时,气体的导热系数升高的幅度和材料本身导热系数的升高幅度远不相同,从而大大影响聚酰亚胺纤维的热导率随温度变化的特性。 聚酰亚胺纤维的阻温系数随温度的关系如图10所示。 阻温系数定义为热扩散系数的倒数,温度为0 K时的阻温系数为残余阻温系数,反映了极低频率的声子散射过程。根据王信伟[20]对阻温系数描述:从能量传递到结构尺寸中的研究,阻温系数随温度变化的趋势可以反映材料缺陷对热导率造成的影响。若材料的物理结构不随温度发生变化,那么阻温系数随温度的下降而下降,并且趋于残余阻温系数,在本实验中,样品1的阻温系数可以用Θ=9.56×105×exp(-149.72/T)+3.30×105来表示,样品2的阻温系数可以用Θ=9.99×105×exp(-176.17/T)+4.41×105来表示,在本实验中,测得聚酰亚胺纤维的阻温系数随温度升高而升高,这说明聚酰亚胺纤维结构随温度变化稳定的结论。 实验利用瞬态电热技术测量出聚酰亚胺纤维在10~290 K内18个温度的热扩散系数,得出聚酰亚胺纤维随着温度的降低热扩散系数单调升高、热导率单调降低的结论。根据阻温系数计算出样品1和样品2的德拜温度分别为299.44和352.34 K,说明温度降低对晶格振动、声子浓度和声子平均自由程等之间的关系,并研究结晶率对聚酰亚胺纤维热导率的影响,且聚酰亚胺纤维结构随温度变化稳定。研究低温下聚酰亚胺纤维的热导率及德拜温度等对其在绝热性方面的应用具有一定意义,同时随着研究的不断深入,通过改变结晶率、改善工艺等方法,制备满足不同生活、生产、科研需要的聚酰亚胺纤维。3.3 材料缺陷对聚酰亚胺纤维热导率的影响
4 结 论

