一种融合社区结构信息的网络表示学习算法
刘彦北,刘金新,耿 磊,王 雯
(1.天津工业大学 生命科学学院,天津 300387;2.天津工业大学 天津市光电检测技术重点实验室,天津 300387;3.天津工业大学 电子与信息工程学院,天津 300387)
网络与人们的生活息息相关,例如社交网络、学术引用网络和蛋白质-蛋白质相互作用网络。网络表示学习又称网络嵌入,旨在通过捕获拓扑结构和属性信息来学习网络节点的低维表示,是一种有效的网络分析手段。它可以克服原始网络表示在分析任务中遇到的许多困难,例如计算复杂度高、并行性低和机器学习方法不适用[1]。网络嵌入在各种后续网络处理任务如节点分类[2]、节点聚类[3]、链接预测[4]和可视化[5]等方面表现优异,已引起了学者浓厚的兴趣。
根据保留网络的信息类型,可以将已有的网络嵌入算法分为3类:结构和属性保留算法、辅助信息保留算法和高级信息保留算法。结构和属性保留算法[6]旨在保留网络中节点之间的结构信息和在嵌入过程中影响网络发展的属性信息。辅助信息保留算法通过融合丰富的辅助信息(例如引文网络中的节点内容或标签,社交网络中的节点和边属性以及异构网络中的节点类型[7])来获得更好的节点表示。高级信息保留算法[8]是指在特定任务中利用监督或伪监督信息。
根据网络嵌入中捕获信息的方式,可以将已有的网络嵌入算法大致分为3类:基于随机游走的算法[9-11]、基于矩阵分解的算法[12-15]和基于深度学习的算法[16-19]。基于随机游走的算法在网络上执行截断的随机游走,并生成随机游走路径以保持节点之间的邻接关系。例如DeepWalk[9]对网络节点执行随机游走,发现随机游走序列中出现的节点分布与自然语言单词的分布相似。因此,该算法扩展了经典的单词表示模型Skip-Gram[10]以学习节点表示。Node2vec[11]改进了DeepWalk中随机游走的生成方法,使生成的随机游走序列可以反映深度优先采样(DFS)和广度优先采样(BFS)的特征,从而改善网络的嵌入效果。基于矩阵分解的算法将网络中的信息转换为矩阵形式,并对矩阵进行分解以获得节点表示。例如TADW[12]、HOPE[13]和M-NMF[14]等算法试图通过分解矩阵(捕获了网络中各种信息)来学习节点表示。这些捕获的信息包括结构关系、文本内容以及各阶邻近度。近年来,许多算法包括LINE[15]、PTE[6]、DeepWalk[9]和Node2vec[11]均被证明等效于矩阵分解。随着深度学习的迅猛发展,基于深度学习的网络表示方法被提出。该方式主要利用非线性函数学习模型以获得节点表示。文献[16]提出的GCN将深度学习中的卷积操作应用到非欧结构的网络数据上,以此来融合目标节点周围邻居节点的信息。文献[17]提出的GAT方法在GCN的基础上使用注意机制确定节点邻域的权重,提高了聚合特征信息的准确性。在GAT的基础上文献[18]提出了关联性图注意力网络,整合了图卷积神经网络(GCN)+注意力机制+关联性的优点。文献[19]提出的LC-GNN利用未连接但具有相同标签的节点对扩大了GCN和GAT这一类方法中节点的接受范围。尽管基于深度学习的算法提供了端到端的学习解决方案,但它们具有较长的训练时间和复杂的参数。
上述方法主要集中在保持结构关系(基于随机游走的算法)或最小化重构误差(基于矩阵分解的算法和基于深度学习的算法)两方面。但是,现存的这些算法中仍然存在一个巨大的挑战,那就是作为网络结构重要特征的社区结构信息[20]通常被忽略了。社区结构在网络中占有极其重要的位置,因为它从更高的层次揭示了网络的组织结构和功能组件[21],因此,捕获原始网络中的社区结构是嵌入学习中的关键步骤。
本文设计了一种融合社区结构信息的网络嵌入(CINE)模型,具体来说,将可以揭示网络组织结构的模块度[21]思想纳入基于矩阵分解的模型中,以提取社区结构信息。与同样研究社区结构信息的Wang等[21]提出的算法相比,本文所提算法的主要创新点在于不仅仅捕获了社区结构信息,还将低阶网络结构信息和节点属性信息同时融合到了节点表示中,设计了一个整体的目标函数,并使用共轭梯度算法进行优化。最后在3个基准数据集上用获得的嵌入结果进行节点分类,通过链路预测实验来评估所学节点低维表示的有效性。
1 CINE模型
1.1 CINE模型构建
CINE的模型框架如图1所示。首先将捕获了节点之间的一阶和二阶邻近性的相似度矩阵分解为不同的组成部分;然后使用模块化约束以挖掘网络中的社区结构;最后联合优化,获得低维的节点向量表示。
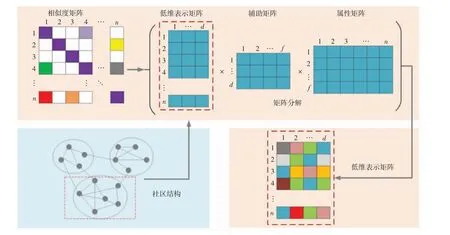
图1 CINE模型框图Fig.1 Diagram of CINE mode
(1)建模结构和属性信息。借鉴TADW的建模思想,在矩阵分解的基础上利用归纳完成矩阵的思想将文本特征合并到节点表示中。计算公式为:
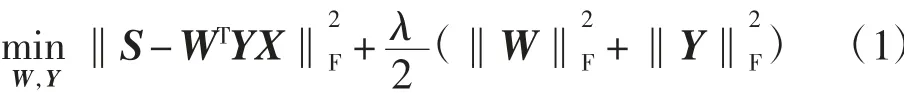
式中:S为捕获节点之间一阶和二阶邻近性的相似度矩阵;W为节点的低维表示矩阵;Y为辅助矩阵;X为节点文本特征矩阵;λ为控制参数。TADW是一种基于矩阵分解的模型,通过合并属性特征来获得更好的网络表示。
(2)建模社区结构信息。首先引入社区结构这个概念,在参考基于模块度最大化[22]的社区检测方法后对社区结构进行建模。模块度的定义为:

式中:ki为节点i的度;如果节点i属于第1个社区则hi=1,否则hi=-1;如果边是随机放置的,则kikj/2e为节点i和j之间的期望边数。因此,直观地说,模块度本质是度量落在社区内的边数与随机放置边的等价网络中的期望边数之间的差。模块度矩阵定义为B∈Rn×n,其中Bij=Aij-(kikj/2e),使得Q=hTBh/4e,h=[hi]∈Rn表示社区指示向量,如果大于两个社区则为社区表示矩阵H,式(2)化简为:

式中:tr(X)为矩阵X的迹;A为邻接矩阵;B∈Rn×n为模块度矩阵;H∈Rn×k为社区指示矩阵。H的约束是确保只有一个元素在每一行中为1,其余为0。因此,每个节点仅属于一个社区。
结合式(1)、式(3)将社区结构引入属性网络的表示中,得到:
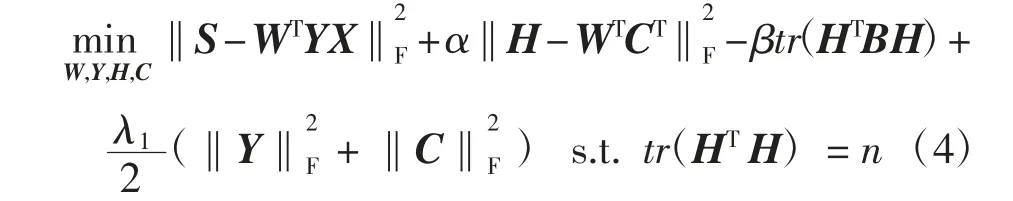
式中:α和β为用于调整相应项贡献的参数;C∈Rk×d为社区表示矩阵。矩阵C的第r行(Cr)为社区r的表示。假设节点i属于社区r,则节点i的表示类似于社区r的表示。相反,如果节点i不属于社区r,则该节点的表示向量与社区r的表示向量正交。根据此假设,本文所提模型期望WTCT的结果可以近似社区指标矩阵H,这样保证了同一社区的节点更相似,从而在节点表示学习中获取了社区结构。
式(4)中,第1项捕获网络中节点级别邻近度;第2项通过矩阵分解将社区结构信息吸收到低维矩阵W中;模块度项约束社区指标矩阵H来更好地捕获网络中的社区分布;最后1项通过调整参数λ1来防止过拟合。
整个CINE模型具有2个优点:首先CINE能够捕获社区结构信息,以使所学的嵌入表示更好地表达原始网络的组织结构和功能组件;其次是将社区结构信息、节点级别的邻近度和属性信息融合到一个目标函数中进行联合优化,这样学习的节点表示更加完善。
1.2 CINE模型优化
首先将目标函数方程(4)简化为:

虽然f(W,H,Y,C)相对于W、H、Y和C同时来看是非凸函数,但在采用交替迭代方法后,即W、H、Y和C中的3个变量固定,相对于仅剩的一个变量而言转化成为该变量的凸函数。此时,整体目标函数的非凸问题就可以转化为关于4个变量的4个凸函数的求解问题,正确初始化W、H、Y和C后再采用共轭梯度下降法寻找出最优解即可。
(1)H步:给定W、C、Y,求解目标中H的子问题。目标函数可以写成:
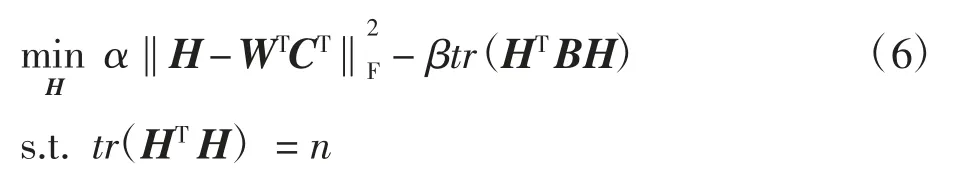
式中:H为社区指标矩阵,由于约束项,使等式(6)的优化成为一个非确定性多项式(NP)难题。参照MNMF[14],放松对HTH的约束为HTH=I后可解决上述问题。最后加入正则化系数λ2将式(6)转换为:

式中:λ2>0应该足够大以确保满足正交性,本文在实验中将λ2设置为103。
(2)Y步:给定W、H、C,求解式(5)中Y的子问题。目标函数可以写成:
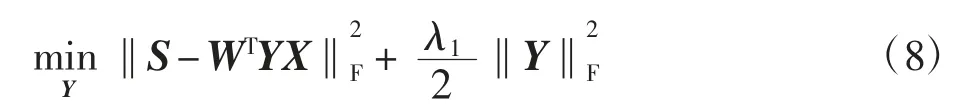
(3)C步:给定W、H、Y,求解式(5)中C的子问题。目标函数可以写成:
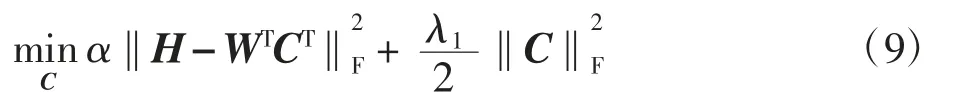
(4)W步:给定H、Y、C,求解式(5)中W的子问题。目标函数可以写成:

(5)然后,使用共轭梯度算法分别进行迭代优化。算法流程如下。
输入:网络G={V,E,X},维度d,社区的数量k,参数α,β,λ。
随机初始化W、Y、H、C并且计算S和B。
H-步:给定W、Y、C使用共轭梯度下降法针对式(7)优化H。
Y-步:给定W、H、C使用共轭梯度下降法针对式(8)优化Y。
C-步:给定W、H、Y使用共轭梯度下降法针对式(9)优化C。
W-步:给定Y、H、C使用共轭梯度下降法针对式(10)优化W。
输出:直到目标函数收敛,输出节点表示矩阵W。
1.3 复杂度分析
本节主要分析CINE算法的时间复杂度。根据式(6)—式(9)中的更新规则计算时间复杂度,分别需要O(n2k+ndk),O(nnz(S)+ndf+nf2),O(nd2+ndk)和O(nd)。其中,nnz(·)表示非零条目的数量。由于d,k,f< 本文采用Cora、Citeseer和Wiki等3个公开网络数据集验证CINE在节点分类、链接预测和可视化任务中的表现。Cora和Citeseer是2个引文网络,网络中不同主题的文档作为节点,文档之间的引用作为边缘。Wiki是一种语言网络,其中文档之间的超链接充当边缘。对于所有数据集,文档的内容对应于节点特征,这些节点特征由相应文档的词袋表示。表1给出了3个数据集的详细信息。 表1 数据集详细信息Tab.1 Details of dataset 为了证明本文所提出CINE算法的有效性,将其与DeepWalk[9]、Node2vec[11]、GraRep[23]、LINE[15]、HOPE[13]、TADW[12]等6种经典的网络嵌入方法进行比较。其中,DeepWalk[9]为基于随机游走的网络嵌入方法,使用截断的随机游走保留节点上下文的结构信息;Node2vec[11]为基于偏向随机游走的网络嵌入方法,使用深度优先采样(DFS)和广度优先采样(BFS)图搜索来获得比DeepWalk更高的质量和更多的信息表示;GraRep[23]为基于矩阵分解的网络嵌入方法,使用奇异值(SVD)分解来保留全局结构信息;LINE[15]为适用于大规模网络数据的网络嵌入方法,使用负采样来优化目标函数,保留了节点之间的一阶和二阶接近度;HOPE[13]为基于矩阵分解的网络嵌入方法,使用SVD分解相似矩阵而不是邻接矩阵来保留高阶接近度;TADW[12]为基于矩阵分解的网络嵌入方法,使用归纳完成矩阵保留节点的文本特征。 实验过程中比较方法的参数默认使用原作者的设置,本文实验所用数据集及对比方法复现调用OpenNE开源库,链接如下:https://github.com/thunlp/OpenNE。对于CINE,设置α,β∈{0.01,0.05,0.1,0.5,1}和λ1∈{0.1,0.2,0.3,0.5,0.6,0.7,0.8,0.9,1}。与此同时,本文使用SVD对属性信息X进行预处理,将其简化为一个200维矩阵。为了公平起见,所有嵌入方法的表示维度统一设置为128。 随机抽取一定百分比的标记节点作为训练集,其余作为测试集,样本训练集的比例占数据集的10%至90%;采用LIBLINEAR软件包[24]训练分类器,进行了10次实验,所有算法都采用微平均(Micro-F1)和宏平均(Macro-F1)评估指标,具体结果如表2—表4所示。 表2 Cora数据集上的分类结果Tab.2 Classification results on Cora dataset 表3 Wiki数据集上的分类结果Tab.3 Classification results on Wiki dataset 由表2—表4可以看出,CINE的分类性能始终高于其他基线方法。CINE和TADW这2种方法优于仅捕获网络结构信息的其他传统嵌入方法,这表明在网络中融合属性信息可以更好地学习节点表示。与此同时,在3个数据集上CINE的性能都显著高于TADW,充分证明捕获社区结构可以更好地表达网络的结构信息,并有助于分类任务。 表4 Citeseer数据集上的分类结果Tab.4 Classification results on Citeseer dataset 采用网络10%的边缘作为测试集,剩下90%的边缘作为训练集。重复实验10次以获得平均结果,并采用ROC曲线下面积(AUROC)为评价指标,如图2所示。 由图2可知,CINE在3个数据集上均达到了最好的效果。从Cora数据集的AUROC得分来看,与Node2vec、DeepWalk和TADW相比,CINE分别得到了1.165、1.144和1.059倍的相对提高。这些结果验证了学习网络节点表示时捕获社区结构的必要性。 图2 链路预测实验结果Fig.2 Experiment results of link prediction 采用t-SNE[25]包对CINE和典型基线方法执行可视化任务,利用结果进行更直观地比较分析。由于3个数据集效果类似,本文只展示了Cora数据集上的可视化结果,如图3所示。图3中,不同的颜色代表不同的类别。 由图3可以看出,与DeepWalk相比,TADW和CINE可以更好地分离不同类别的数据点,这表明融合属性特征使得节点学习到的网络信息更加丰富。与TADW相比,CINE中相同类别的数据点彼此靠近,不同类别的边界线更加明显,这证明捕获社区结构后节点表示可以更好地表达网络的组织结构信息。 图3 可视化实验结果Fig.3 Visualized experimental results 本文提出了一种新颖的融合社区结构信息的网络嵌入模型(CINE)。在嵌入过程中,CINE使用矩阵分解来融合节点的1阶、2阶节点邻近度信息以及属性信息,在模块度的指导下捕获社区结构,设计一个统一的目标函数,采用共轭梯度算法对其进行优化,并在Cora、Wiki、Citeseer3个真实数据集上验证了所提出模型的有效性。结果表明: (1)在分类任务中,CINE采用90%训练集在3个数据集上的Micro-F1分数分别达到0.900 2、0.840 2、0.761 9,优于所有对比算法; (2)在Cora数据集的链路预测任务中,CINE的AUROC得分比Node2vec、DeepWalk和TADW分别提高了1.165、1.144和1.059倍; (3)CINE算法在保留了从更高层次揭示网络组织结构和功能组件的社区结构信息后,所学习的节点表示可以更好地完成后续各种网络分析任务。2 实验验证
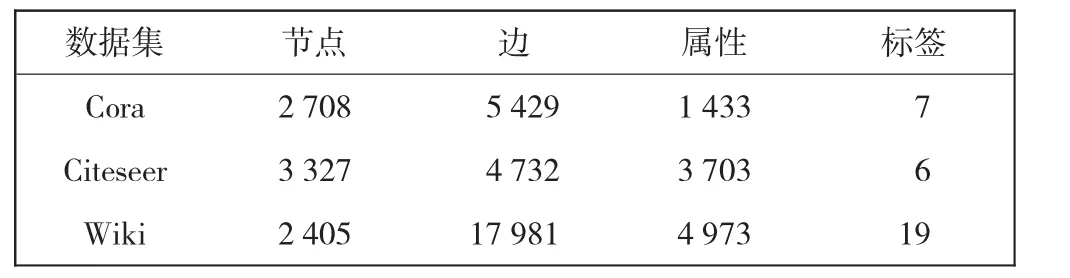
2.1 节点分类
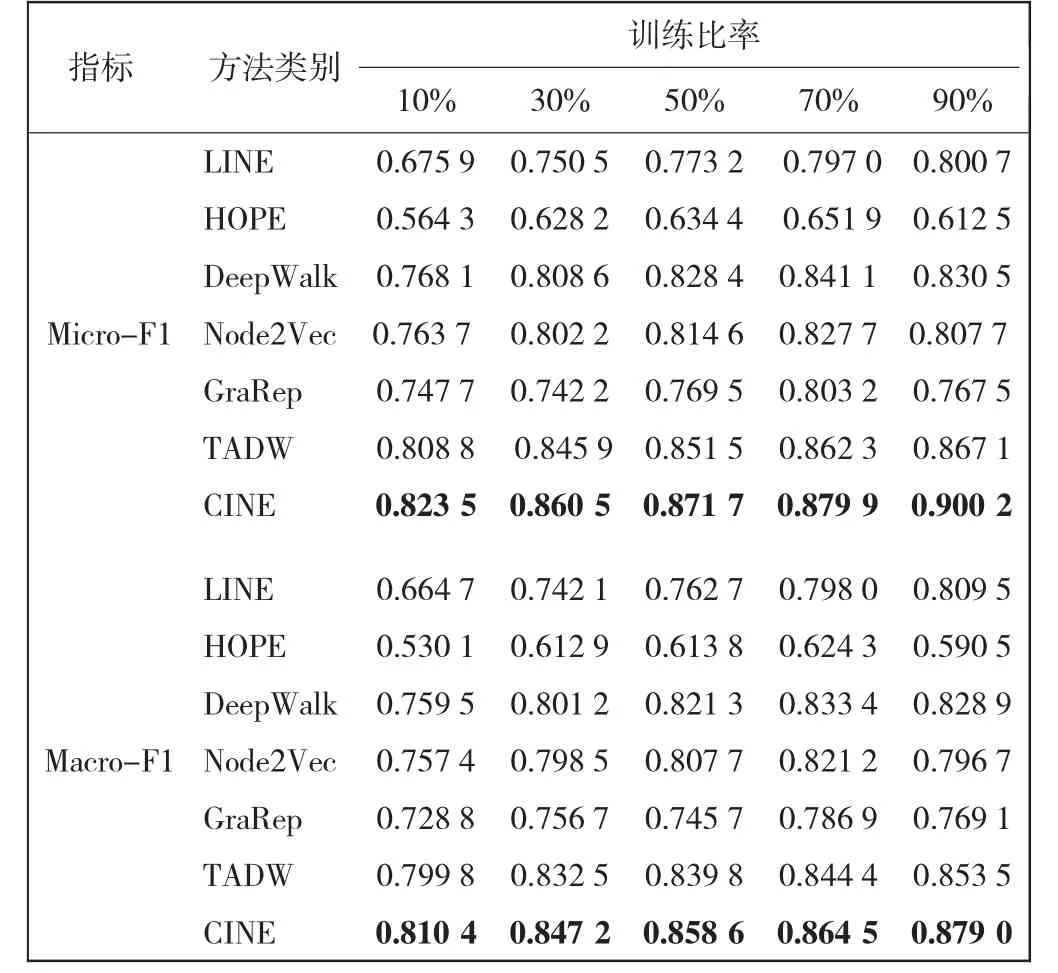
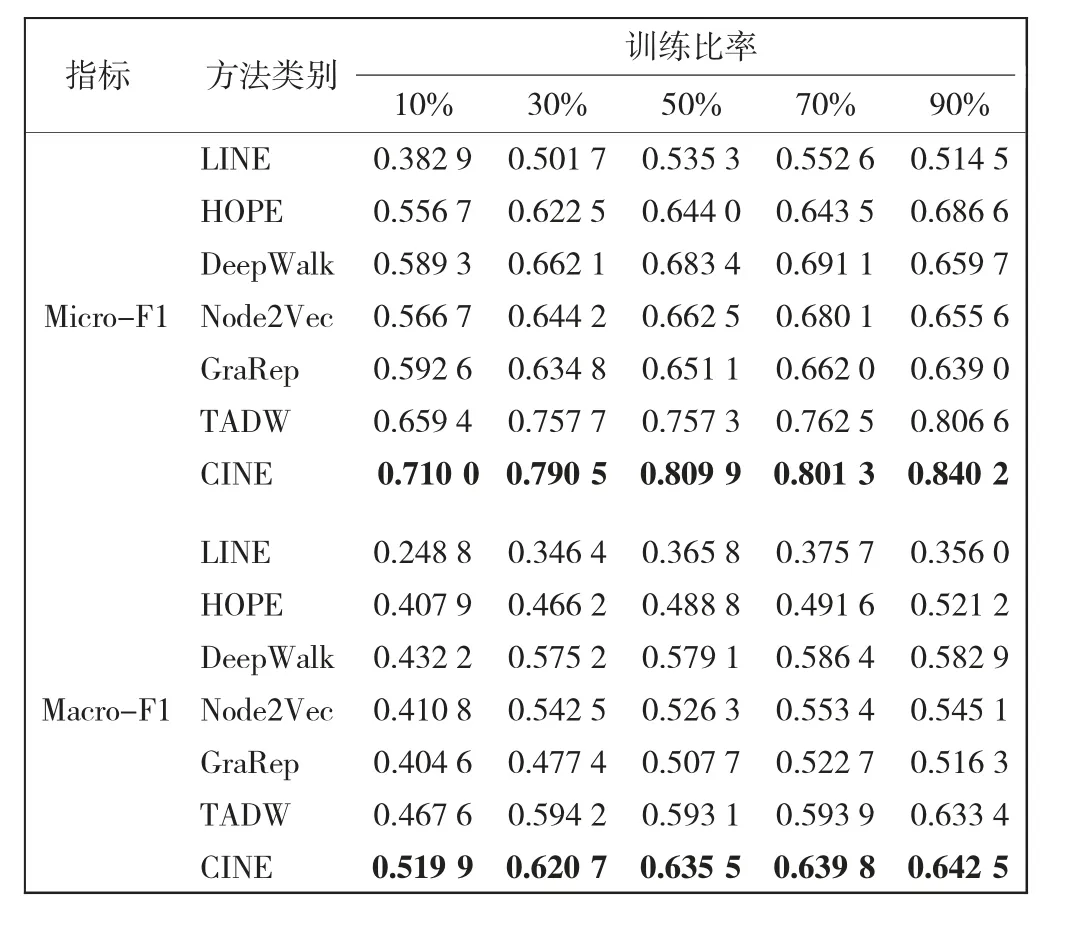
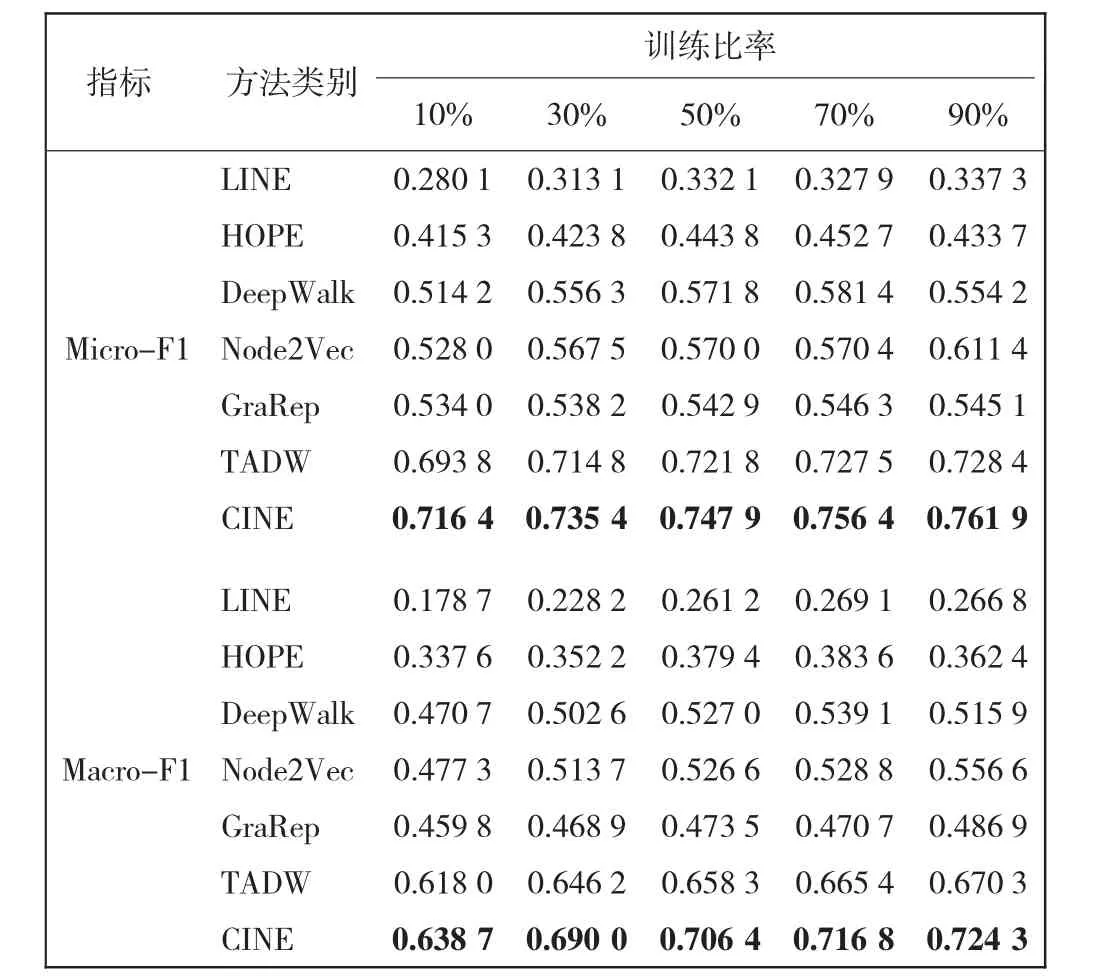
2.2 链路预测

2.3 可视化

3 结论

