基于变论域模糊PID的航空转台控制系统研究

魏 彬 唐凤轩 梁 畅 张爱军*

(北京化工大学 1.有机无机复合材料国家重点实验室；2.机电工程学院，北京 100029)

引 言

航空转台可模拟飞行器在空中的姿态角，实现半实物模拟仿真分析，从而快速、安全和有效地对制导和控制系统及相关器件的安全性和可靠性进行评估，并根据仿真结果作出相应的改进以达到飞行器总体设计的性能指标[1]，因此广泛应用于飞机试飞、导弹制导等特殊环境的试验测试中。国防工业的进步对航空转台的控制精度提出了更高的要求，针对航空转台控制系统进行研究对于促进我国国防工业的发展具有重要意义。

目前在世界范围内，美国Auctrionic公司一直是航空转台业内翘楚，其研发的转台产品HD7736的控制精度可达0.001″，定位误差小于0.005″[2]；国内在航空转台领域的研究起步较晚，北京航空精密机械研究所研制的SGT-550测试转台是最具代表性的产品，其精度可达1″，位置分辨率优于0.000 01°[3]。控制方法是航空转台控制系统研究的核心，控制方法的选择对转台控制系统的性能有巨大影响。当前广泛用于工业控制系统的控制算法主要有传统的比例-积分-微分(proportion integral differential, PID)控制算法、复合控制算法以及Smith 预估控制策略。Boldbaatar 等[4]将自学习模糊滑模控制首次应用于水温控制，取得了良好的控制效果。自McCulloch 和 Pitts[5]提出神经元模型后，经过半个多世纪的发展，神经网络模型已经从简单的模型向深层神经网络模型发展，其非线性逼近能力更优。Hu等[6]第一次使用近端策略优化强化学习算法优化随机控制策略来控制无模型四旋翼飞行器速度，大大提高了模型速度跟踪的准确性和鲁棒性。Xu等[7]使用分数阶微积分理论的分数阶PID控制器控制转向油缸的运动，在瞬态响应、跟踪能力和鲁棒性方面均取得良好的效果。

模糊PID是在模糊控制论诞生后发展起来的一种控制策略，在工程上有广泛应用。聂放[8]利用遗传算法对模糊 PID 控制进行优化，将遗传算法的模糊PID控制器和标准模糊PID控制器进行比较的结果表明，前者性能明显优于后者；Oliveira等[9]提出一种新的线性规划方法，用于设计两输入两输出(TITO)系统的对角模糊PID 控制器，并提出基于补偿特征轨迹的设计方法，实验结果表明线性规划方法提高了对角模糊PID的控制效率；谢少华等[10]将模糊控制与直流电机调速结合起来，验证了基于模糊PID的直流电机调速系统的可靠性；胡国良等[11]提出利用遗传算法设计模糊车辆半主动悬架磁流变阻尼器的PID控制系统，仿真结果表明该控制系统具有优越的减振性。

国内转台厂商大多采用传统PID加高阶前馈网络校正的方法补偿误差，这种方式对工况质量的要求较高，且依赖于技术人员的现场调试，无法实现控制参数的在线整定。为解决这一问题，本文设计了一套航空转台随动控制系统，相较于传统控制策略转台，其具有较好的工况适应性，对人员调试水平的依赖度更低，且将粒子群优化模糊PID控制策略与集成化控制卡相结合，有利于转台领域应用模糊控制策略的小成本迁移。对基于粒子群优化的变论域模糊PID进行研究，在MATLAB环境下完成仿真验证，选取航空转台测试平台硬件，利用Labwindows/cvi和可编程多轴运动控制卡(PMAC)脚本语言作为控制软件编写环境，完成航空转台测试平台的整体设计，并使用航空转台测试平台对本文所述方法进行了验证。

1 系统硬件设计

航空转台测试平台由台体和控制系统组成。为了达到高精度的定位性能，需要选取合理的电气元件，同时采用可靠的控制策略，从而完成转台的实时控制并显著提升其定位精度。

转台台体由运动控制器、力矩电机以及配套的驱动器和编码器组成；控制系统则是由形成位置闭环、完成控制策略的PMAC下位机和运行图形用户界面(graphical user interface，GUI)的工控上位机组成。转台控制系统的整体结构如图1所示。

该系统的工作原理如下：编码器实时采集转子位置，通过60孔扁平线缆发送给运动控制器，控制器接受上位机命令，将目标位置与反馈位置的偏差输入到PID控制器中，改变驱动器端电压从而实现电机的定位。系统实物如图2所示。

图2 系统实物图

采用工控机作为除运动控制之外的数据流传递工具，完成运动管理、通讯及数据收集与处理。工控机选用SIMATIC IPC847D工控机(德国西门子公司)，运动控制模块选用经典PMAC运动控制卡(美国Delta Tau公司)，该控制卡的速度、分辨率、带宽等性能指标优越，契合转台控制场景[12]。选用KEB COMBIVERT F5-MULTI型驱动器(德国科比传动技术有限公司)，反馈元件采用RON786增量式编码器(德国HEIDENHAIN公司)，电机选用160LYX35型力矩电机(包头长安永磁电机有限公司)。电机参数如表1所示。

表1 电机参数

2 模糊PID控制策略

提出一种使用粒子群迭代寻优策略以得到最优化调节参数的方法。通过变论域模糊PID控制保证控制系统的动态抗干扰能力，使用粒子群优化算法优化PID参数和变论域伸缩因子，增加初始设置的模糊规则利用度，在MATLAB/simulink环境下进行仿真。

2.1 粒子群优化策略

粒子群优化(particle swarm optimization, PSO)算法是一种用来求解问题最佳解决方案的寻优算法[13]，可以获得一定范围内待求解问题的最优解。在控制领域，可以将PSO 算法与 PID 控制器结合使用，实现参数的动态调整[14]。粒子群优化算法基于由群体智能建立的简化模型，个体可获得群体运动，使问题的解决有序化，从而获得最佳解决方案[15]。图3所示为本文应用的粒子群优化算法流程图。首先进行优化参数的初始设定，初始化粒子后计算个体与群体的位置及适应度，判断是否满足终止条件，若满足则输出结果，不满足则更新粒子，形成迭代。

图3 粒子群优化流程

为了判断各个粒子值与理论解的接近程度，应当确定一个合理的评价指标，并适配力矩电机的模型特点。本文选取误差积分准则中的时间乘绝对误差积分准则(ITAE)指标作为评价粒子值与理论解接近程度(粒子群适应值)的函数[16]，ITAE指标的表达式为

(1)

式中，e(t)为实际值与设定值之间的偏差；t为优化时间。

从表达式(1)可以看出，ITAE指标可以作为超调量、调节时间、上升时间等变量的表征参数。本文将ITAE指标作为衡量控制过程控制性能的综合评价因素，即粒子群适应值反映了超调量、调节时间、上升时间等综合参数的情况。

2.2 模糊PID控制器设计

模糊控制器本质上是基于误差e、误差变化率ec的PID参数自调整型控制器，同时利用e和ec的变化率来动态调整输入变量的伸缩因子α(e)、α(ec)和输出变量动态整定值LK(m)(m=p,i,d)，以此实现论域因子的自动整定[17]。模糊PID控制器的变论域结构如图4所示。

图4 模糊PID控制器变论域结构

依据Mamdani等[18]提出的min-max推理准则，加权平均解模糊处理后的输出为

(2)

PID参数整定公式为

Kp=Kp0+ΔKp

Ki=Ki0+ΔKi

Kd=Kd0+ΔKd

(3)

式中，Kp0、Ki0、Kd0均为PID参数的初始设定值；ΔKp、ΔKi、ΔKd均为模糊控制PID解算出的动态整定值。

根据工程整定经验，e、ec和PID的自调整量ΔKp、ΔKi、ΔKd在函数形式上均为三角函数分布。建立ΔKp、ΔKi、ΔKd的控制规则，以ΔKp为例，如表2所示，其中NB、NM、NS、ZO、PS、PM、PB分别代表负大、负中、负小、零、正小、正中、正大，是表征输入和输出变量模糊化后的模糊语句。

表2 ΔKp模糊控制规则

则系统的实际输出值为

(4)

为了最大程度地提高模糊规则的利用度，更好地优化控制指标，可通过伸缩因子和比例因子动态调整模糊PID控制器的输入和输出。对于输入变量的量化因子，考虑对模糊规则的最大利用，采用量化因子与输入变量正相关的原则，从多种描述方式中选择在电机控制领域有广泛应用的形式[17]：α=1-λ1e-kx2；对于输出变量的比例因子，结合PID各个参数对控制性能的影响，采用Kp和Kd的比例因子与误差单调一致，而Ki的比例因子又与误差具有单调反向性的原则，来得出比例因子的经验公式。本文总结的伸缩因子和比例因子的经验公式如式(5)所示。

(5)

通过粒子群优化算法完成式(5)中各个参数的求取。利用2.1节的粒子群优化算法，设定惯性因子为0.6，加速常数为2，本文研究的调整函数中量化因子与比例因子的伸缩因子公式中共有7个参数λ1、λ2、λ3、λ4、λ5、k1、k2，再加上PID的3个初始参数Kp0、Ki0、Kd0，设定维数为10，粒子群规模为30，最大迭代次数为30，最小适应值设置为0，最大迭代次数和最小适应值可作为算法的终止条件，速度最大值和最小值分别为2和-2，10个优化参数解向量的上区间为[5 2 000 0.01 1 1 1 1 1 3 3]，下区间为[1 1 000 0.001 0 0 0 0 0 0 0]。粒子群初始化后代入ITAE指标求解，保存个体与群体的历史位置和适应度，进行终止判断，如未满足终止条件则重新设定参数进行下一轮求解，以此形成迭代，直到达成寻优终止条件。

迭代过程中的适应值变化如图5所示。

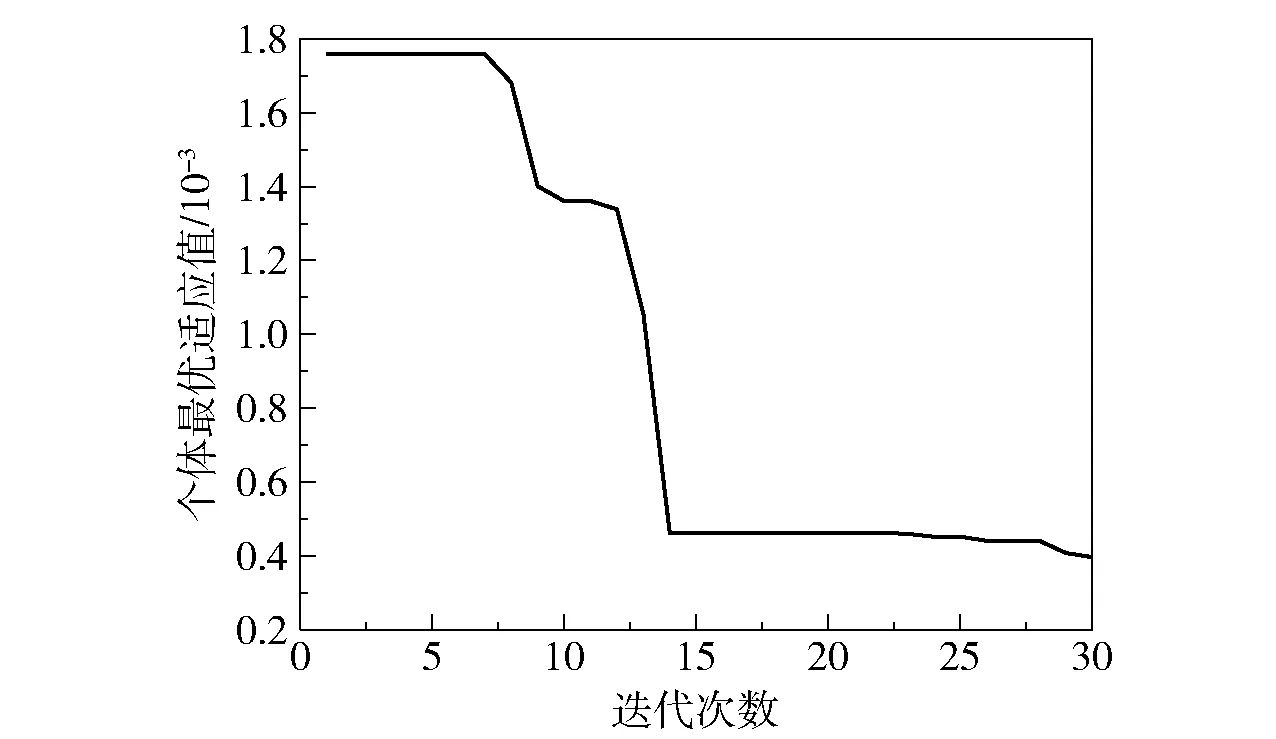
图5 个体最优适应值变化

计算出参数最优解为[Kp0，Ki0，Kd0,λ1,λ2,λ3,λ4,λ5,k1,k2]=[2.246,1 533.861,0.003 5,1,1,1,1,0,0.384,0]。通过粒子群算法迭代寻优，设定迭代次数为30。由图5可以看出，当迭代次数在0～7时，种群位置更新较慢，个体最优适应值保持稳定；当迭代次数在7～14时，适应值随迭代次数的增加而大幅下降；当迭代次数大于14时，个体最优适应值继续保持稳定状态，系统适应度函数指标已经趋于稳定；迭代次数大于24之后有小幅度下降。在实际应用中可根据实验精度要求设定迭代次数，次数越多，精度越高。

2.3 系统建模与分析

仿真系统由力矩电机近似仿真模型、定义粒子群优化的MATLAB脚本程序以及调用simulink模型的MATLAB函数组成。其中脚本的粒子群优化算法通过引用适应度函数模型得到适应值，根据适应值在线优化参数，将优化过程参数储存在工作空间中，与近似仿真模型实现数据交互，在定义粒子群优化的MATLAB脚本程序中实现迭代寻优。

在模糊控制器的设计中，利用MATLAB中的模糊控制工具Fuzzy工具箱可以快速便捷地进行输入以及输出变量的定义，因此本文使用Fuzzy工具箱进行模糊控制变量的相关设计，如图6所示。

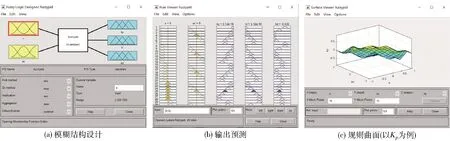
图6 模糊控制变量设计

给定初始转速(1 000 r/min)后，计算输入量e和ec，之后输入变论域模糊PID控制器，经过变论域调整环节和矩阵运算，输出PID参数调整变量ΔKP、ΔKi、ΔKd，再累加至KP、Ki、Kd。依据ITAE指标，将仿真得到的适应度函数输入到粒子群算法程序中进行下一步优化，得到参数的最优解，进而得到模糊PID的最优化模型，如图7所示。

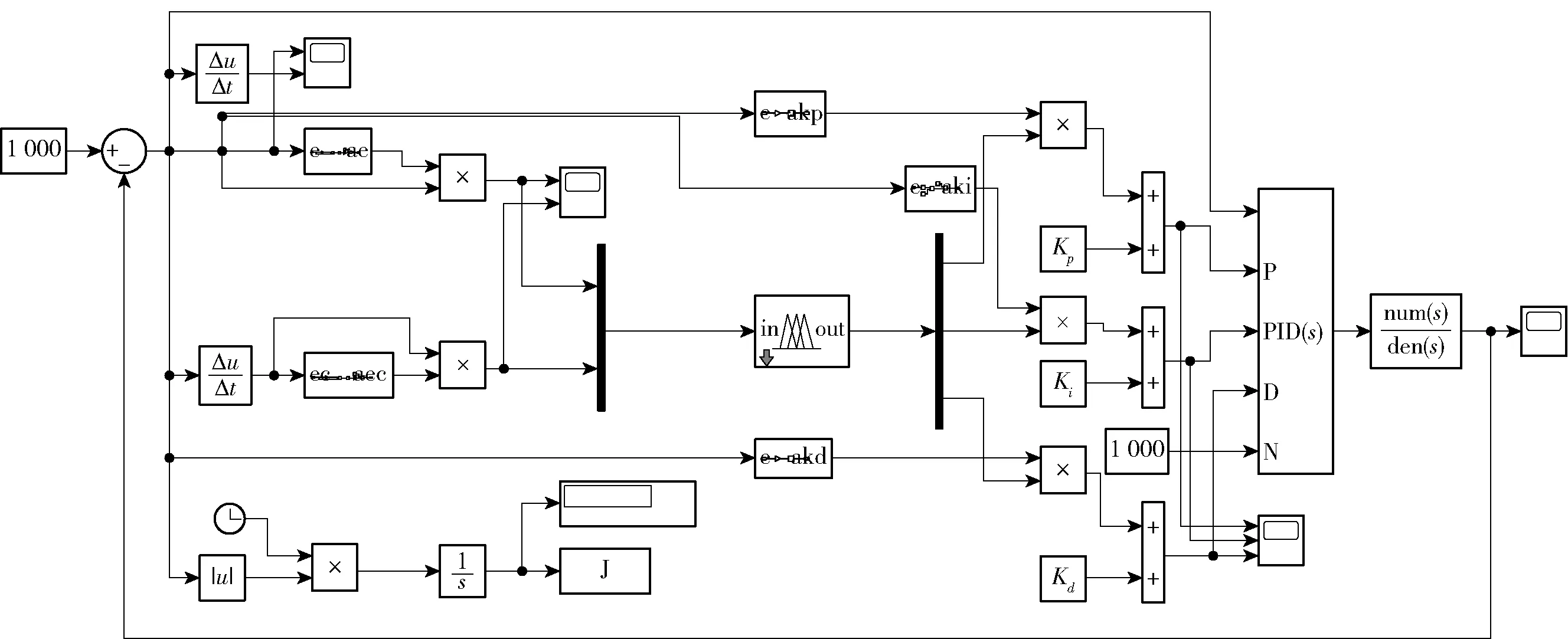
图7 模糊PID的simulink模型

将通过优化算法获得的最优解代入变论域模糊PID控制系统模型中，即[Kp0，Ki0，Kd0,λ1，λ2,λ3,λ4,λ5,k1,k2]=[2.246,1 533.861,0.003 5,1,1,1,1,0,0.384,0]，设置电机模型启动的期望转速为1 000 r/min，启动负载为10 N·m。当t=0.05 s时，外部负载突增至20 N·m。粒子群优化的模糊PID控制策略、未优化的模糊PID控制策略和常规PID控制策略的转速和转矩阶跃响应如图8所示。

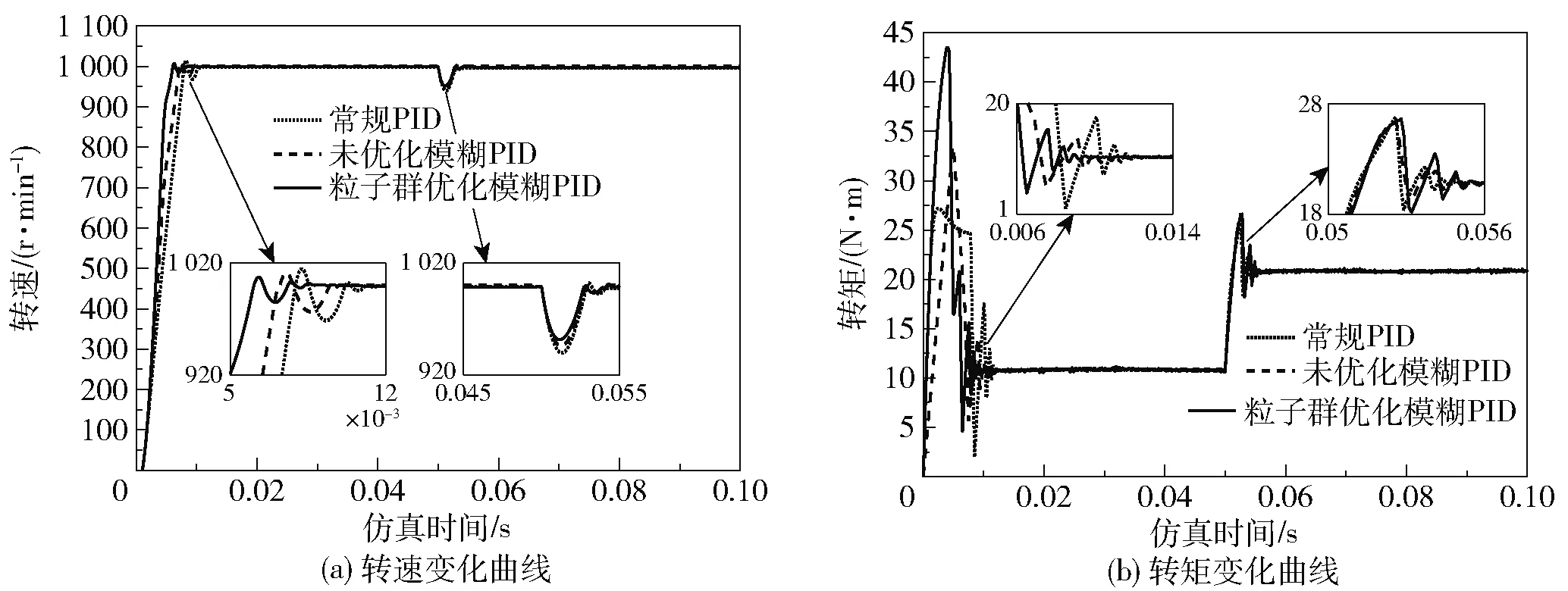
图8 转速与转矩的阶跃响应

从图8(a)可以看出，常规PID控制的转速上升最慢且存在较大超调，未优化的模糊PID控制的转速表现相较于常规PID有所提升；而相较于未优化的模糊PID控制，粒子群优化的变论域模糊 PID 控制的转速上升更快且超调量更小。在对系统施加负载扰动后，三者均有动态扰动响应，而优化的变论域模糊PID控制的超调量更小，稳定性更好，说明其具有更好的抗干扰能力和鲁棒性。从图8(b)可以看出，变论域自适应模糊PID控制能使电机转矩更快地达到稳定，波动较小，抗干扰能力强。如图8所示，当负载在0.05 s发生变化，优化过的模糊PID控制相较于其他控制策略在转速方面超调更小，转矩响应更快速，可及时跟踪负载的变化情况。

综上可得出：粒子群优化的论域可变模糊PID 控制的超调量更小、调节时间更短，对于负载扰动有更好的调节适应效果，使得系统的跟随特性好、稳定性和抗干扰能力强。

3 系统软件设计

控制系统由上位机和下位机组成，上位机完成粒子群迭代和模糊PID的运算后，通过外设部件互连标准(peripheral component interconnect，PCI)总线与下位机通信，物理上采用60孔扁平线缆，在运动控制器的可编程逻辑控制器(programmable logic controller, PLC)中定义双口随机读取存储器(random access memory, RAM)，控制程序中写入双口RAM地址，进而实现打开控制器、发送运动命令、收集位置信息等后续流程，控制算法对位置误差进行有效补偿，提高控制精度[19]。转台控制系统软件结构如图9所示。

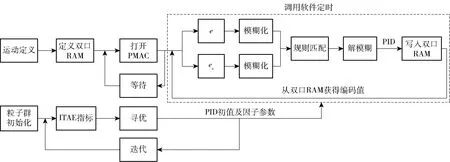
图9 软件结构

使用Labwindows/cvi作为开发环境，编写可视化操作界面，通过操作界面完成对转台的指令下发与转台状态的实时监测，操作界面如图10所示。

图10 上位机运行界面

航空转台实验平台控制通过上位机可视化界面采集运行数据，如输入信号类型、幅值、周期和相位等，在上位机中完成集成PSO优化的变论域模糊 PID 算法运算。PMAC运动控制器中定义了双口RAM地址，上位机通过PCI总线将运行通讯输入到PMAC运动控制器中，运动控制器在双口RAM地址中采集运行数据。应用位置式数字 PID 控制算法完成转台的实物控制，观察具体的控制性能曲线，判断其控制性能。

在转台空载运行时，输入幅值为1°、频率为1 Hz的正弦信号。在传统PID下，即上位机不经过模糊PID动态整定运算，直接将恒定PID参数传递给PMAC运动控制器，在输入信号激励下，实验平台正弦响应及输入输出信号相减得到的误差如图11所示。

图11 常规PID的正弦响应和误差

打开上位机模糊PID自整定系统，设定粒子群优化算法惯性因子为 0.6，加速常数为2，维数为10，粒子群规模为30，最大迭代次数为30，最小适应值为0，速度最大值和最小值分别为2和-2。经过粒子群优化后，在幅值为1°、频率为1Hz的输入信号激励下，实验平台正弦响应及输入输出信号相减得到的误差如图12所示。

图12 模糊PID的正弦响应和误差

通过上述正弦信号跟踪仿真曲线的对比可以看出，应用了模糊控制器的航空转台可将正弦跟踪误差从0.1°降至0.05°以内。转台能够精确地到达指令位置值处，并且误差保持在有效要求范围内，取得了更好的位置随动效果。

4 结论

以粒子群优化求解最优参数的变论域模糊PID结构方法为控制策略，设计了航空转台控制系统。在MATLAB/simulink中搭建航空转台控制系统仿真模型，与常规PID和未经粒子群优化的模糊PID相比，所提控制策略的转速响应超调量更低，调节时间更短，转矩响应更快达到稳定且波动较小，抗干扰能力较强。选取以PMAC运动控制器为核心的航空转台测试平台硬件，使用Labwindows/cvi编写测试平台控制软件上位机部分、PMAC脚本语言编写下位机部分，搭建航空转台测试平台并进行算法验证，实验结果显示，应用了变论域模糊PID的航空转台测试平台将正弦跟踪误差从0.1°降至0.05°以内。综合仿真和实验结果，基于变论域模糊PID的控制系统使航空转台的控制精度得以显著提升，超调量更小，调节时间更短，抗干扰能力强，同时具备实用性，极大地提高了航空转台的控制系统随动性。