分数阶热弹理论下重力对压电介质中波传播的影响

马永斌, 张建敏

(兰州理工大学 理学院, 甘肃 兰州 730050)

经典热弹性理论认为热波的传播速度是无限的，但后来的实验发现这与物理事实不符，为解决这一问题，学者们发展了广义的热弹性理论.目前广泛应用的是Lord-Shulman[1](L-S)广义热弹性理论和Green-Lindsay[2](G-L)广义热弹性理论.基于广义热弹性理论，学者们进行了大量的研究工作.自从Abel开始运用分数阶导数求解等时曲线问题中积分方程的解之后，分数阶微积分便被用来修正很多现有的物理模型，尤其是在粘弹性、热传导等领域.对于许多材料及物理过程，例如生物材料、低温过程等，在此情形下经典理论和广义热弹性难以准确描述其热弹性行为.因此将分数阶微积分引入广义热弹性理论十分必要.Sherief等[3]在L-S理论的基础上加入Caputo型分数阶导数，提出一种新的分数阶广义热弹性理论，建立一种新的分数阶广义热弹性耦合理论.何天虎等[4]基于Sherief等提出的分数阶热弹性理论对无限长圆柱导体模型研究了其广义电磁热弹耦合问题的动态响应.Sherief等[5]在广义热弹性扩散理论的基础上，采用拉氏变换和傅里叶变换研究了厚板受到热冲击和化学扩散的边界问题.刘泽权[6]基于该理论研究了二维纤维增强弹性体受热冲击载荷的电磁热弹耦合问题.马永斌等[7]基于分数阶热弹性理论，研究了含有球型空腔无限大体的热冲击动态响应.

Youssef等[8]将Riemann-Liouville分数阶积分算子引入广义热传导方程，得到新的分数阶广义热弹性耦合理论.Sarkar等[9]基于Youssef等提出的分数阶广义热弹性耦合理论研究了各向同性旋转弹性介质热弹性耦合问题，运用正则模态法分析了不同分数阶参数下介质内场的变化.Youssef等[10]建立具有分数阶应变的三维广义热弹性模型，分析了不同分数阶参数下介质内各物理场的变化.Sunita等[11]基于Youssef等提出的分数阶广义热弹性耦合理论，研究了均匀各向同性弹性介质在双温及磁场作用下的物理场分布，得到位移、应力、温度、应变的表达式.

Ezzat等[12]在考虑分数阶双相滞后热传导规律的基础上，建立了一种新的双温磁热弹性数学模型，建立另一种分数阶广义热弹性耦合理论.Ezzat等[13]在热传导的背景下考虑记忆依赖效应，建立了电热弹性耦合的数学模型，并将计算结果与经典耦合理论的结果进行了比较.Kumar等[14]基于该分数阶热弹性理论，研究了双温条件下平面波在热弹性介质边界的反射，得到入射角度不同情况下反射波的振幅变化.Magdy等[15]在上述分数阶理论基础上，考虑热传导与记忆依赖效应，建立新的磁热弹性理论模型，并与经典耦合理论进行比较.

学者们对于热弹性材料的研究多是基于各向同性的材料进行的，然而随着压电材料的广泛应用以及其不同于各向同性材料的材料特性，学者们大量研究了压电材料的热弹性行为.Chandrasekharaiah[16]首次提出了压电介质的热弹性理论，并且得出能量方程中解的唯一性.Noda等[17]提出了压电复合材料板的弯曲行为理论，并且基于压电效应和热电效应的经典叠层理论，给出了求解方法.El-karamany等[18]提出了压电介质的广义线性热弹性模型.Singh[19]基于G-L理论建立了广义热弹性压电材料的控制方程，研究了压电介质中的波传播问题.

然而，目前对于压电材料的研究大多忽略材料的重力作用，对于压电材料，考虑重力的分数阶广义热弹性理论的研究尚不多见.本文基于Ezzat等[12]建立的分数阶热弹性耦合理论，考虑电场，研究压电材料特性参数与温度相关的空间半无限大体同时受应力冲击和热冲击作用的热弹响应问题，弥补压电材料对考虑重力方面研究的不足.

1 基本方程

本文采用均匀各向异性热弹性压电介质，建立半无限大体模型，z轴方向与介质平面垂直.介质中所有的场量都用坐标x，z和时间t表示.各向异性热弹性介质的基本方程在下面给出.

1) 运动方程[20]

(1)

式中：σij表示应力；ui表示位移分量；ρ表示物质密度；Fi表示体力分量.

2) 静电方程(高斯方程)

Di,i=0

(2)

3) 热传导方程[12]

(3)

式中：Kij是热传导系数；θ=T-T0为温度增量；T为温度；T0为初始温度；Ce为恒应变比热；γij为热模量；τ0为热松弛时间.

4) 本构方程

压电材料的本构方程表示为

σij=cijklεkl-eijkEk-γijθ

Di=eijkεjk+υijEi+piθ

(4)

式中：cijkl为弹性常数；eijk为压电系数；Ei表示电场强度；υij表示介电常数；Pi表示热电常数.

位移应变关系及电场电势函数关系

(5)

式(1～5)中，逗号后面加后缀表示对坐标的导数，上面加点表示对时间t的导数.

2 问题描述

对于半无限大空间模型，上述本构方程转化如下：

对于半空间问题，所有的变量都依赖于时间t和坐标x,z.对于二维问题，假设位移向量的分量形式如下：

u1=u(x,z,t),u2=0,u3=w(x,z,t)

(8)

则由运动方程(1)可以得到

(9)

式中:g为重力加速度，由式(2)和式(7)得

(10)

定义如下的无量纲变量

(11)

式中

将方程(3,9,10)根据方程(11)进行无量纲化.除特别说明外，以下讨论均采用无量纲量，并略去“′”.

(12)

(13)

(14)

(15)

式中

(16)

本构方程(6,7)无量纲表达形式如下：

(17)

(18)

3 正则模态法

计算中所涉及的物理变量的解可以按照正则模态法表示

{θ,u,w,φ}(x,z,t)={θ*,u*,w*,φ*}(z)e(iξx+ωt)

(19)

利用式(19)，式(12～15)可表示为

(D2+A1)u*+(A2D+A3)w*+

A4Dφ*+A5θ*=0

(20)

(A6D+A7)u*+(D2+A8)w*+

(A9D2+A10)φ*+A11Dθ*=0

(21)

A12Du*+(A13D2+A14)w*+

(D2+A15)φ*+A16Dθ*=0

(22)

A17u*+A18Dw*+(A19+D2)θ*=0

(23)

式中

(24)

式中

(25)

消去方程(20～23)中u*,w*,θ*,φ*的任意三个函数，得到

(26)

式(26)中的Bj(j=0,1,2,3)的取值如下：

B0=(A1A8A15A19-A1A10A14A19-

A3A7A15A19-A5A8A15A17+

A5A10A14A17)/(1-A9A13)

B1=(A1A8A15-A1A10A14-A3A7A15+

A1A8A19-A3A7A19-A5A8A17+

A1A15A19-A5A15A17+A8A15A19-

A10A14A19-A2A6A15A19-A1A9A14A19-

A1A10A13A19+A2A10A12A19+

A4A6A14A19-A4A8A12A19+A5A6A15A18+

A1A10A16A18-A1A11A15A18-

A2A10A16A17+A2A11A15A17+

A4A8A16A17+A5A9A14A17-A5A10A12A18+

A5A10A13A17-A4A11A14A17)/(1-A9A13)

B2=(A1A8-A3A7+A1A15+A1A19-A5A17+A8A15-A10A14+A8A19+A15A19-

A2A6A15-A1A9A14-A1A10A13+

A2A10A12+A4A6A14-A4A8A12-

A2A6A19+A5A6A18-A1A11A18+

A2A11A17-A4A12A19+A4A16A17-

A9A14A19-A10A13A19+A10A16A18-

A11A15A18-A1A9A13A19+A2A9A12A19+

A4A6A13A19+A1A9A16A18-A2A9A16A17-A4A6A16A18-A5A9A12A18+A5A9A13A17+A4A11A12A18-A4A11A13A17)/(1-A9A13)

B3=(A1+A8+A15+A19-A2A6-A4A12-

A9A14-A10A13-A11A18-A1A9A13+

A2A9A12+A4A6A13-A9A13A19+

A9A16A18)/(1-A9A13)

当z→∞时，式(26)的解如下:

{u*(z),w*(z),θ*(z),φ*(z)}=

(27)

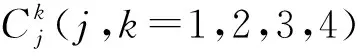
m8+B3m4+B2m4+B1m2+B0=0

(28)

将式(27)代入式(20～22)，得到以下关系

(29)

式中

(30)

可以得到

(31)

将式(31)代入式(17,18)得到的应力和电位移的表达式

(32)

(33)

4 边界条件

4.1 应力边界条件

假设只产生正应力大小为σ0(不含切应力)，则有

σ13(x,0,t)=0，σ33(x,0,t)=-σ0e(iξx+ωt)

(34)

4.2 热力学边界条件

在表面z=0，θ对z的一阶导数为零.因此有

θ(x,0,t)=θ0e(iξx+ωt)

(35)

4.3 电场条件

在z=0时，电场强度为零，因此有

(36)

(41)

因此，所涉及的场变量，如温度、位移、电势、应力和电位移的变化趋势均可用图形的形式反映出来.

5 数值结果及分析

计算中，半空间无限大压电介质采用材料特性参数如下：

c11=7.41×1010N/m2
c13=3.93×1010N/m2
c33=8.36×1010N/m2
c55=1.32×1010N/m2
ρ=5 504kg/m3,Ce=260J/(kg·K)
T0=298 K-1,K1=K3=9 W/(m·K)
γ1=6.21×105N/(m2·K)
γ3=5.51×105N/(m2·K)
e31=-0.160C/m2,e33=0.347C/m2
e15=-0.138C/m2
υ11=8.26×10-11C2/(N·m2)
υ33=9.03×10-11C2/(N·m2)
p3=-2.94×10-6C/(m2·K)

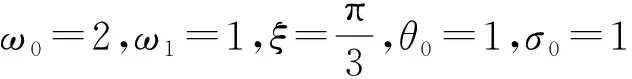
图1～图6给出了x=1,g=0，考虑三个不同的r(r=0.50,r=0.75，r=1.00)值，位移、温度、应力和电势沿z轴的变化.

图1显示水平位移u始终为正值，在z≈0.1处取得峰值，随着位置远离边界水平位移也相应减少，最终趋向于零.分数阶参数取不同值时，对位移u的影响不大.图2显示无量纲位移w沿z轴的分布情况.位移w在边界处取得最大值，随着位置远离边界而减少，最终趋向于零.相对于位移u，分数阶参数取不同值对位移w的影响不大，这主要是热弹性材料在两个方向上的材料性质不同造成的.

图1 r取不同值,位移u在z轴上的分布(g=0) Fig.1 Distribution of dimensionless displacement u on z-axis at different r(g=0)

图2 r取不同值,位移w在z轴上的分布(g=0) Fig.2 Distribution of dimensionless displacement w on z-axis at different r(g=0)

图3显示温度θ在z≈0.5处达到峰值，然后随着z轴远离热源而降低，最终收敛于零.随着分数阶参数的增加，计算得到的温度的峰值也增加.图4显示应力σ11满足边界条件，在z≈0.5的位置达到峰值(同时也靠近温度最高的位置)，温度对应力σ11有较大影响.应力σ11随着z取值增加呈上升趋势，最终收敛于零.分数阶参数增加，计算得到的应力σ11峰值的绝对值增加.

图3 r取不同值,温度θ在z轴上的分布(g=0)

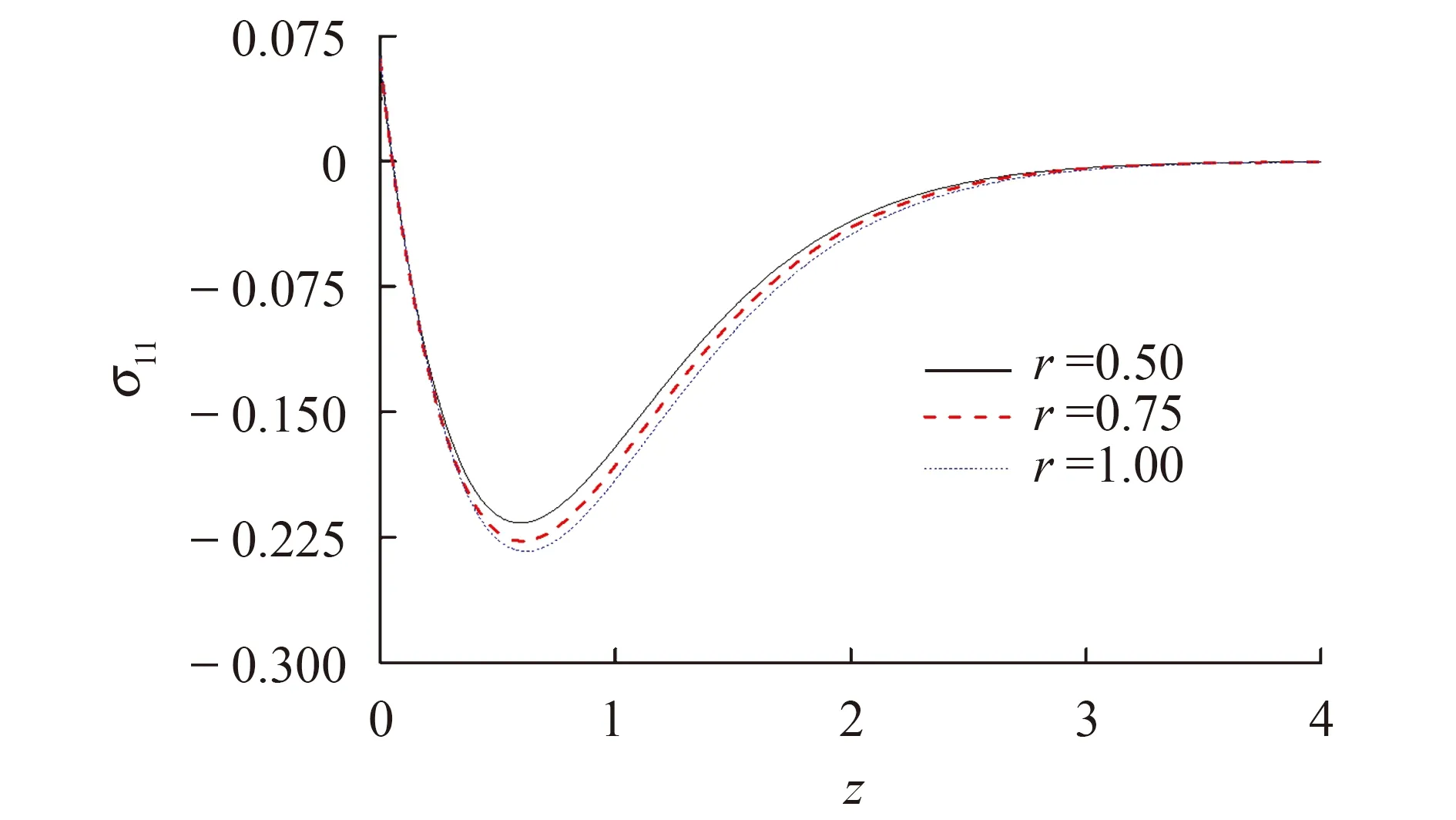
图4 r取不同值,应力σ11在z轴上的分布(g=0) Fig.4 Distribution of dimensionless stress σ11 on z-axis at different r (g=0)

图5显示无量纲应力σ13满足边界条件，在z≈0.25处达到最小值，随着z取值增加，应力σ13的值增加，最终趋向于零.分数阶参数取不同值时，对应力σ13的影响不大.图6显示无量纲电位移D1沿z轴分布情况，电位移D1在边界处绝对值最大，随着z取值远离边界，电位移D1的值增加，最终趋向于零，不同分数阶参数对应的电位移D1的值相差不大.

图5 r取不同值,应力σ13在z轴上的分布(g=0) Fig.5 Distribution of dimensionless stress σ13 on z-axis at different r(g=0)

从图1～图6可以看出，物理量的变化不仅依赖于空间，还依赖于分数阶参数，随着z值的增加，各物理量呈下降趋势，最终收敛于零.这表明在该模型中，x方向坐标值不变，z坐标值越大的位置，热冲击对各物理量的影响越小.

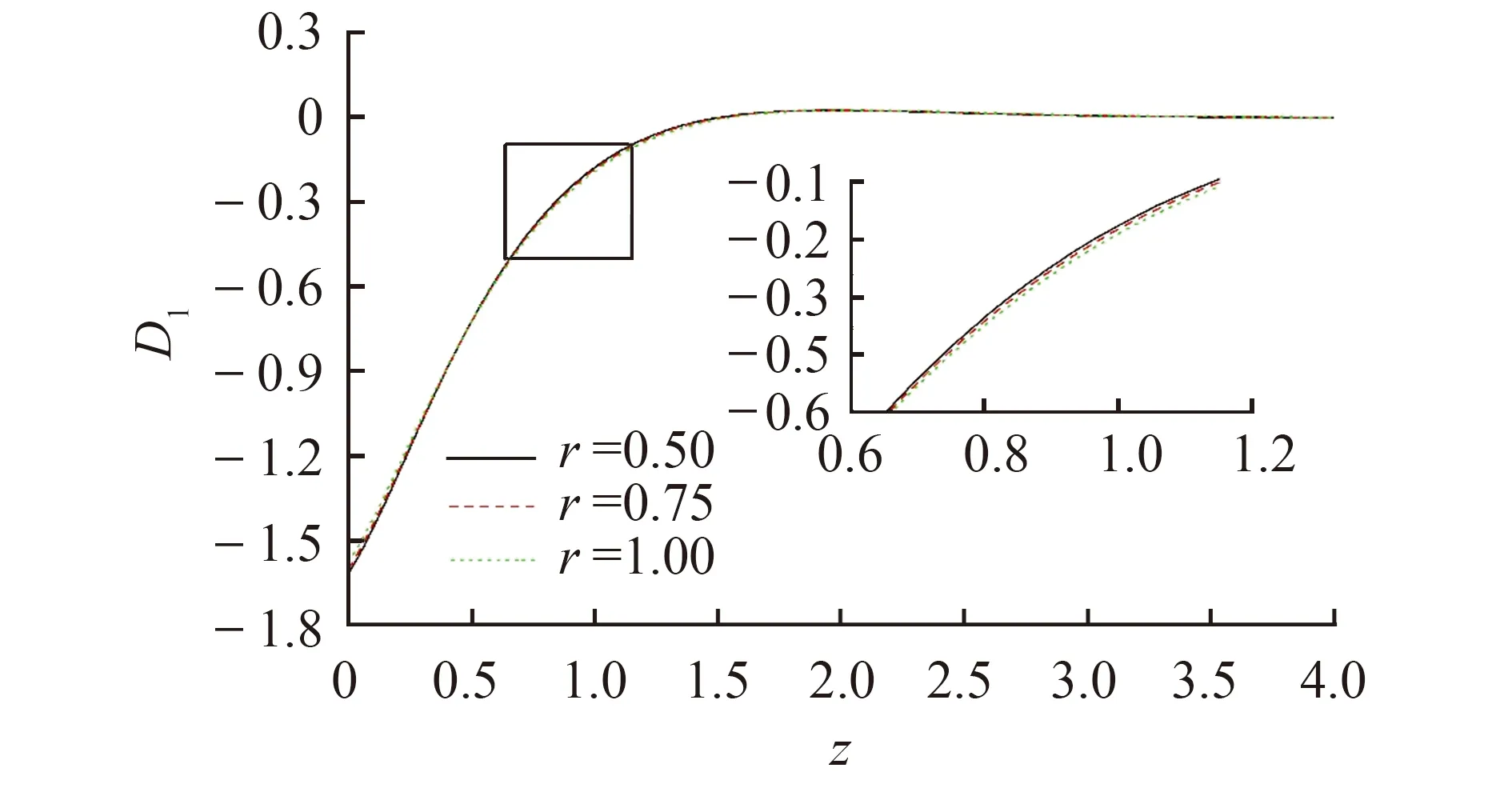
图6 r取不同值,电位移D1在z轴上的分布(g=0)Fig.6 Distribution of dimensionless electric displacement D1 on z-axis at different r(g=0)

图7～图12给出了x=1,g=9.8时，考虑三个不同的r(r=0.50,r=0.75，r=1.00)值，位移、温度、应力和电势沿z轴的变化.

图7～图12绘制了在重力作用下，位移u和w、温度θ、应力σ11和σ13、电位移D1六个物理量沿z轴的分布情况.图7显示水平位移u始终为正值，并且在边界处取得最大值，随着z轴远离边界，位移

图7 r取不同值,位移u在z轴上的分布(g=9.8) Fig.7 Distribution of dimensionless displacement u on z-axis at different r(g=9.8)

u逐渐减小，最终趋向于零.在边界处分数阶参数越小预测的位移值结果越大.在远离边界处，分数阶参数越小预测的位移值结果越小.同时对比图1发现，重力影响位移u的分布趋势以及在边界上的数值.图8显示位移w沿z轴的分布，其分布趋势与位移u相似，在边界处取得最大值，随着z轴远离边界，位移值逐渐减小，最终趋向于零，同样在边界处分数阶参数越小预测的位移值越大，在远离边界处，分数阶参数值越小，预测的位移值越小.位移w在边界处的数值不同于位移u，原因是各向异性材料在两个方向上的材料参数不同.对比图2发现，重力影响位移w的分布趋势以及在边界上的数值.

图8 r取不同值,位移w在z轴上的分布(g=9.8)

图9显示不同分数阶参数下，温度θ沿z轴的分布情况.由图可知随着z轴远离边界，温度先逐渐升高后逐渐降低，最终趋向于零.在相同位置，分数阶参数越小，预测的温度数值越小.对比图3发现重力对温度的影响较小.图10显示不同分数阶参数下，应力σ11沿z轴的分布.由图可知，应力σ11的分布先逐渐减小，后逐渐增大，最终趋向于零；分数阶参数越大，预测的σ11的最小值越小.对比图4，可知重力影响其大小及走势.

图9 r取不同值,温度θ在z轴上的分布(g=9.8)Fig.9 Distribution of dimensionless temperature θ on z-axis at different r(g=9.8)

图10 r取不同值,应力σ11在z轴上的分布(g=9.8)Fig.10 Distribution of dimensionless stress σ11 on z-axis at different r(g=9.8)

图11显示不同分数阶参数下，应力σ13沿z轴的分布.由图可知，在边界上应力σ13为零，表明在边界处不存在切应力，随着z轴远离边界，σ13呈现先减小后增大的趋势，最终趋向于零.分数阶参数越小，预测的最小值也越小，对比图5可知，重力影响应力σ13的分布，但最终都趋向于零.图12显示不同分数阶参数下，电位移D1沿z轴的分布.由图可知电位移D1在边界处取得最小值，随着z轴远离边界，D1逐渐增加，最终趋向于零.在z轴的相同位置，分数阶参数越小，预测的电位移D1的值越大，与图6对比发现，重力影响电位移D1的分布趋势.

图11 r取不同值,应力σ13在z轴上的分布(g=9.8)Fig.11 Distribution of dimensionless stress σ13 on z-axis at different r(g=9.8)

从图7～图12可以看出，物理量的变化与空间位置和分数阶参数有关，同时还与重力参数有关.结果表明，重力对热弹性波的影响是不同的，重力影响各物理量的峰值，但是不影响其走势，各物理量最终都收敛于零.表明在该模型中，x方向坐标值不变，z坐标值越大的位置，热冲击对各物理量的影响越小.

图13～图18给出了g=0,r=0.5时,考虑三个不同的x值(x=1.0,x=1.2，x=1.4)，位移、温度、应力和电势在z轴上的变化.

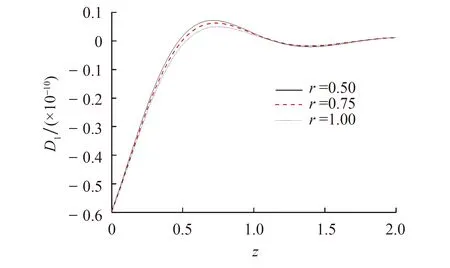
图12 r取不同值,电位移D1在z轴上的分布(g=9.8)Fig.12 Distribution of dimensionless electric displacement D1 on z-axis at different r(g=9.8)

图13 x取不同值,位移u在z轴上的分布(g=0)Fig.13 Distribution of dimensionless displacement u on z-axis at different x(g=0)

从图13～图18可以看出，随着x的变化，各无量纲物理量发生变化.图13显示x取不同值，无量纲位移u沿z轴分布情况.当x取不同值时，位移u都在边界(z=0)上取得最大值.图中显示当x=1.4，位移u的峰值最大，随着z取值增加，位移u的值平稳下降，最终趋向于零.图14显示无量纲位移w沿着z轴分布情况.在固定平面(z取值相同时)，随着x取值增加，位移w的值减小.在x取值不变，位移w随着z的值增加逐渐下降，最终趋向于零.

图14 x取不同值,位移w在z轴上的分布(g=0)Fig.14 Distribution of dimensionless displacement w on z-axis at different x(g=0)

图15显示x取不同值，无量纲温度θ沿z轴分布情况.温度在边界z≈0.2处取得最大值，随着z取值增加，逐渐减小，最终收敛到零.温度场量在x方向存在波动，在x=1.4对应的温度θ小于x=1.0对应的温度.图16显示x取值增加，应力σ11在0≤z≤2范围内的取值也随之增加.应力σ11在边界处取得最大值，随着竖向距离z的增加，逐渐减小，最终收敛到零.

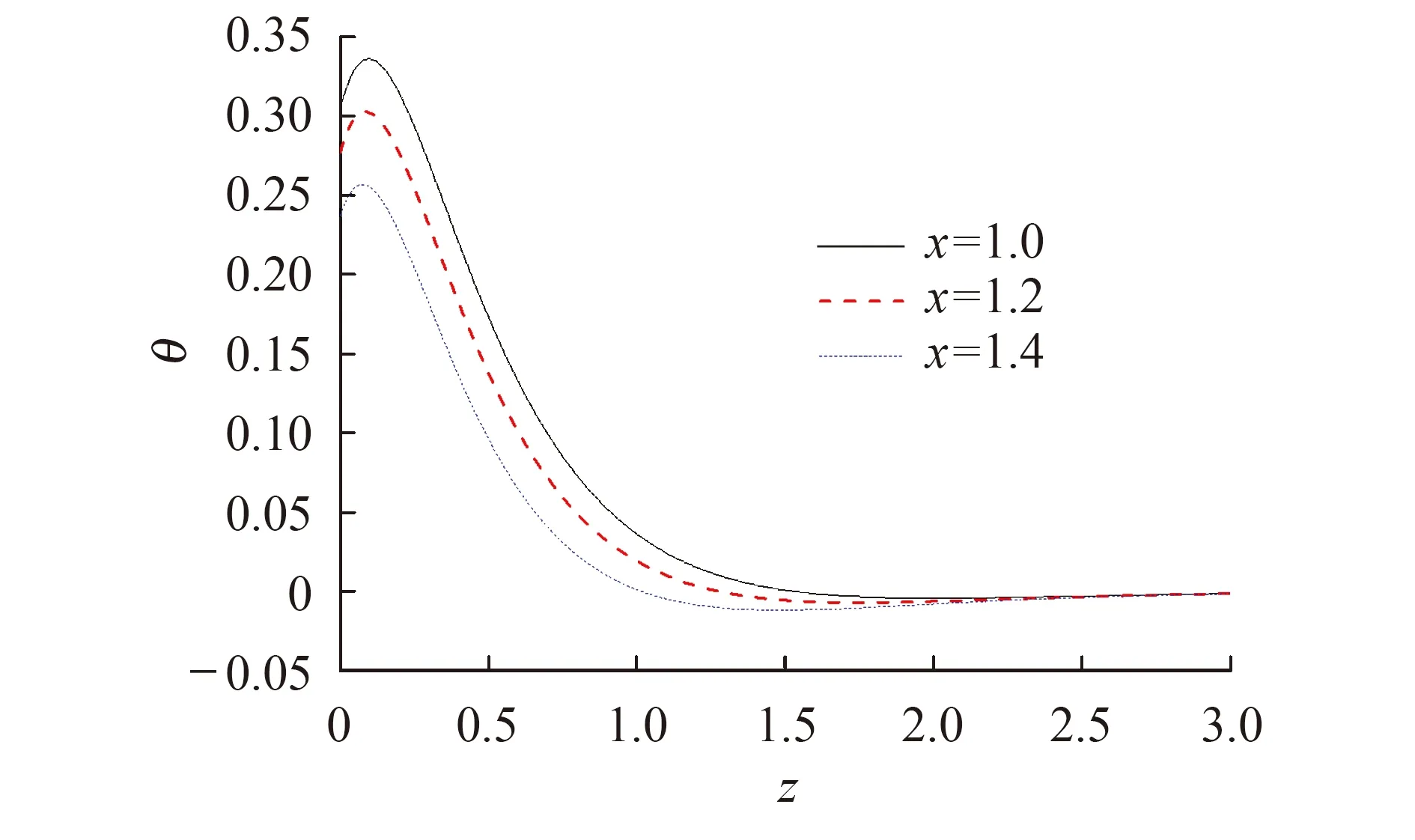
图15 x取不同值,温度θ在z轴上的分布(g=0)

图16 x取不同值,应力σ11在z轴上的分布(g=0)Fig.16 Distribution of dimensionless stress σ11 on z-axis at different x(g=0)

图17显示应力σ13在边界处的值为零，满足边界条件，在z≈0.25处的绝对值达到最大.图中显示x取值增加，应力σ13的峰值增加，随着竖向距离z的增加，逐渐减小，最终收敛到零.图18显示电位移D1始终为负值，在z=0处绝对值取得最大值.图中显示在z取值靠近坐标原点处，x取值的变化对电位移有显著影响.随着z的增加，电位移逐渐增加，最终收敛于零.

图17 x取不同值,应力σ13在z轴上的分布(g=0)Fig.17 Distribution of dimensionless stress σ13 on z-axis at different x(g=0)

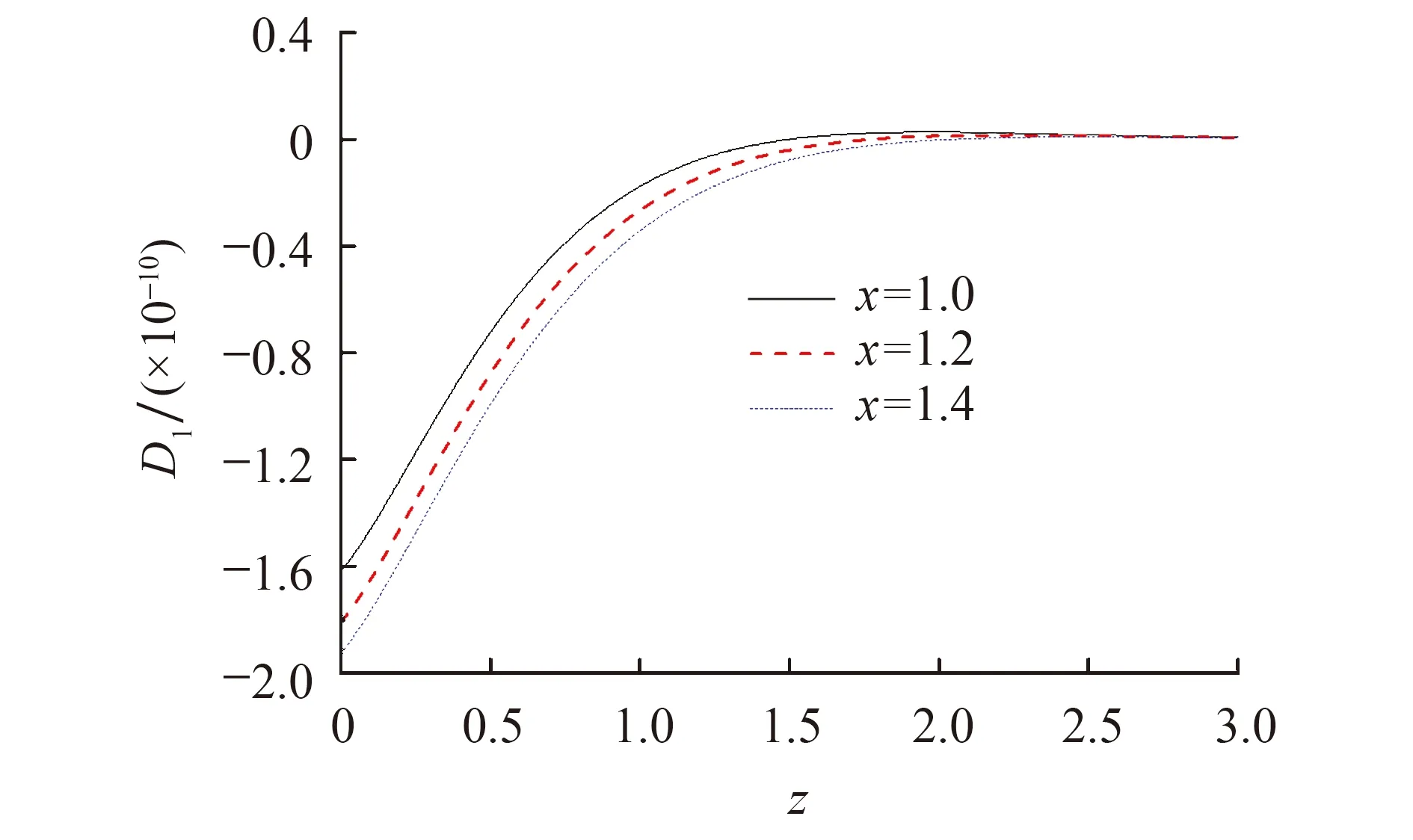
图18 x取不同值,电位移D1在z轴上的分布(g=0)Fig.18 Distribution of dimensionless electric displacement D1 on z-axis at different x(g=0)

取g=0,r=0.5,z=1.0,对轴上的两个固定位置(x=1.0和x=1.4)进行了计算，得到了无量纲位移u，w和无量纲应力σ11随时间的分布规律，如图19～图21所示.

图19 x取不同值,无量纲位移u随时间t的变化Fig.19 Change of dimensionless displacement u with time t at different x

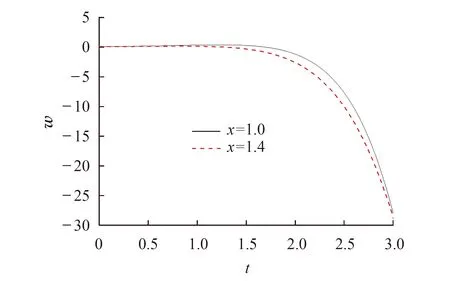
图20 x取不同值,无量纲位移w随t的变化

图21 x取不同值，无量纲应力σ11随时间t的变化Fig.21 Change of dimensionless stress σ11 with time t at different x

图19显示两个固定位置的水平位移从零开始，随着时间的增加而平稳增加.图20显示了两个固定位置的竖直位移w随时间的变化.图中显示每个固定位置的位移w从零开始，随着时间的增加逐渐减小.位移u和w在同一位置的表现不同，是因为热弹性体在两个方向上抵抗变形的能力不同.对于不同点达到相同位移所需的时间也是不同的，距离热源越远，膨胀变形所需的时间越长.距离热源越远，相应位置的位移绝对值越小.这能够反映出热弹波是以有限速度传播的.

图21显示应力分量σ11随时间的分布.结果表明在t≥2.5的范围内，x=1.0位置的应力和梯度大于x=1.4位置的应力和梯度，但是在时间上的分布趋势是相同的.

6 结论

本文基于分数阶热弹性理论，研究了半无限大体受到热冲击和应力冲击时的动态响应，结果显示，重力对各物理量的预测结果有显著影响.由所得结果，可得出如下结论：

1) 在不考虑重力情况下，不同分数阶参数对应的温度、应力、位移、电位移的峰值不同.这说明弹性体的位移、应力、温度、电位移不止与时间t、空间变量x,z有关，还与分数阶参数有关.

2) 重力的存在增加了位移u、w，应力σ11、σ13和电位移D1的波动性.重力对各物理量的峰值有影响，因此重力在该模型中的存在具有重要意义.

3) 计算结果表明，位移u,w的走势不同，是因为该热弹性体模型在两个方向上的力学性质不同.

4) 固定位置的位移u,w，应力σ11随时间t的不同，说明热波的传播速度是有限的.

5) 随着竖向坐标z的增加，各物理量都收敛于零，各物理量都是连续的.