施工及环境因素诱发污水处理池差异沉降及渗漏风险

王颖轶，徐伟忠，刘祥龙

[1.上海交通大学船舶海洋与建筑工程学院，上海市200240；2.上海城建市政工程（集团）有限公司，上海市200065]

0 引言

工程实践和理论分析表明，几乎所有的混凝土构件均是带裂缝工作的，只是有些裂缝很细，甚至是肉眼看不见的微观裂缝（裂缝宽度＜0.05 mm），一般对结构的使用没有大的危害，可允许其存在[1-2]；有些裂缝在使用荷载或外界物理、化学因素的作用下，不断扩展演化，引起混凝土碳化、保护层剥落、钢筋锈蚀等，使混凝土的强度和刚度受到削弱、耐久性降低，严重时甚至发生结构倒塌事故，必须加以控制[3-4]。裂缝的形成与扩展机理复杂、影响因素众多，与混凝土材料及配比、施工质量、养护条件、地质条件等多方面的因素相关[5]。迄今，研究的焦点是服役期混凝土结构在自然环境、地基变形条件不良影响下裂缝形成和扩展问题。例如：（1）在我国东南沿海地区，混凝土结构的沉陷裂缝与自然灾害的相关性；（2）地基受地下水、污水、雨水等长时间浸泡，导致不均匀沉降，从而造成结构混凝土沉陷裂缝。但对于大体积混凝土施工过程中，因非均匀流变软土地基差异沉降、地下水渗透等诱发结构裂缝及其演化尚少见系统研究。

对于某项目的依托工程白龙港污水处理厂提标改造工程，地基土体具有分布不均匀、地下水位受地表水源及近海潮汐影响、地下水位分布不均匀等不良工程地质和复杂水文地质条件影响，大面积基坑开挖及混凝土结构全生命周期具有较大风险及其不确定性。

1 工程因素诱发地基沉降

对于大型污水处理池工程，地基变形主要源自场地降水（井点降水）、地面季节性降水水位变化、海岸潮汐水位变化、基坑开挖卸载后土体流变位移。考虑到季节性雨水不在工程区域产生地下水位大的差异性分布，为简化分析，仅考虑工程井点降水、潮汐水位变化和施工卸载的影响。

1.1 工程场地人工降水

污水处理厂通常靠近河岸、海滨等利于排水的区域建设，工程区域内地层水量相对丰富且渗透性强。渗透性地层基坑开挖过程中，在水头差作用下，易产生渗透、流砂或周边坍塌等现象，影响开挖效率和施工安全。对此，根据基坑开挖深度及土层性质，采用轻型井点、真空管井等降低其水位或含水量。

1.1.1 降水方式

降水方式一般有井点降水和真空疏干管井降水等。（1）井点管：用ϕ48 mm 的PVC，井管长8.0 m，下端装2.0 m 长的滤管，滤管外包尼龙网，并用铁丝绑扎牢固。（2）连接管：用ϕ48 mm 的塑料管与集水总管连接。（3）集水总管：用ϕ65 mm 的钢管，每隔1.5 m设一个连接井点管接头。（4）抽水设备：选用真空泵。

真空疏干井点管井：（1）井壁管：井壁管均采用焊接钢管，降水井井壁管直径均为ϕ273 mm。（2）过滤器：滤水管的直径与井壁管的直径应相同；所有滤水管外均包一层40 目的尼龙网，尼龙网搭接部分约为20%～50%；尼龙网包好用铁丝捆绑牢实。（3）沉淀管：滤水管底部搭接1.00 m 沉淀管，防止井内沉砂堵塞而影响进水；沉淀管底口用铁板封死（见图1）。

图1 降水井现场布置之实景及轻型井点管大样图

1.1.2 井点降水引起地基变形特性

根据白龙港污水处理池设计资料，现场采用成排式真空疏干井管排水方式，沿长轴方向任意横截面水位分布相同（工程地质和水文地质条件相同），简化为竖平面的水位线分布，如图2 所示。函数关系可表达为式（1）所列。

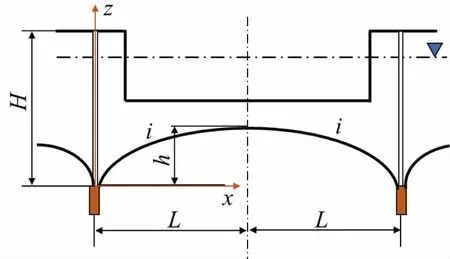
图2 井点间降水水位线图示

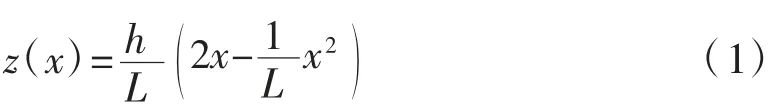
同时，井点降水造成地下水位的变化将不可避免地引起深层土体和地表的沉降位移。迄今大量研究表明，井点管降水引起的地表沉降位移可用式（2）近似表达。

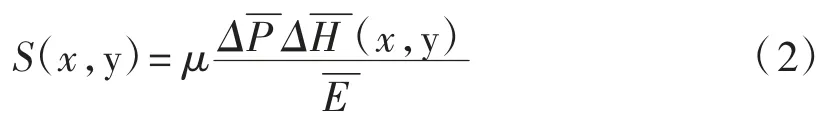
式中：Δ为降水产生的自重附加应力平均值，kPa；为降水深度；为降水深度范围内土层的压缩模量平均值，其调整系数，取值范围为0.5～1.5。

以上海白龙港工程为例，建立工程降水实际水位分布曲线及沉降位移曲线如图3 所示。

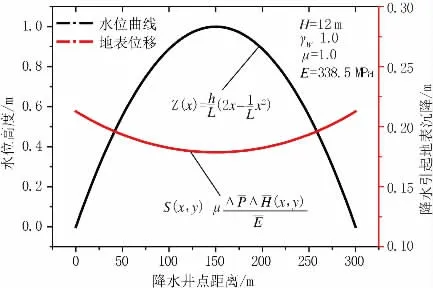
图3 降水水位曲线及地表沉降曲线图

根据沉降公式（2）即可求出对应的曲率半径。

当x=L时，曲率半径具有最小值。

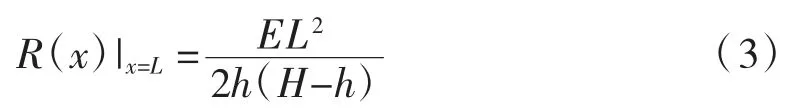
将L=150 m，E=339 MPa，H=12 m，h=1.0 m 代入式（3）可得降水引起地表沉降曲线的最小曲率半径为346 704 m。水池结构周边及其底板混凝土结构最大附加弯曲正应力分别为0.865 MPa 和0.069 MPa。两者均远小于混凝土抗拉强度。

1.2 桩基作用分析

上述分析可知，当材料参数和结构几何参数一定时，地基差异变形状态下其上部结构产生的变形应力与变形曲率成比例关系。在实际工程中，造成地基不均匀沉降的原因有工程场地地质参数的非均匀性、水文地质区域性差异、随环境因素的变化，以及基坑开挖中普遍使用的抗拔工程桩。

为比较分析，取无桩基、单桩、群桩等三种不同的地基加固状态，在工程地质、水文地质开挖方式相同的条件下，采用三维有限元作对比性模拟计算，地基位移分布数值模拟结果如图4 示。

在图4 的上图中，深色点线为无桩基条件下的计算结果，浅色点线为模拟单桩作用下的数值计算结果。其结果显示，桩基作用使得地基的峰值上浮位移降低了约20%。更重要的是桩基有效地降低了地基变形分布曲线的曲率（增大了曲率半径），对缓和地基上部结构的弯曲变形应力十分有效。

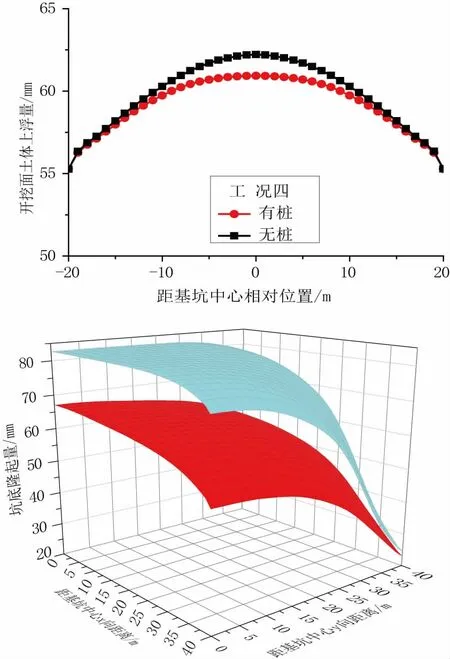
图4 软土地层桩基作用比较图

下图深色曲面为模拟无桩基条件下的基坑开挖坑底地层上浮位移的空间分布，浅色曲面为按4×4 m间排距设置抗拔桩条件下基坑开挖引起坑底上浮位移的空间分布。显然，无桩基条件下地层的上浮位移大于80 mm，且位移曲面的曲率较大。群桩作用，有效抑制了地层的卸载上浮，较大程度上降低了位移量（15%～20%）。同时，群桩作用很大程度上降低了地层位移曲面的曲率，从而有效降低上部结构弯曲应力及结构裂纹萌生发展的风险，提高水池结构抗渗性能。

2 海岸潮汐变化影响

当存在水位差时，地下水体将产生渗透流动。由于地层中物质结构不同，水流路径和渗透系数差异巨大。地下水复杂渗流路径和地层附加变形空间分布如图5 所示。

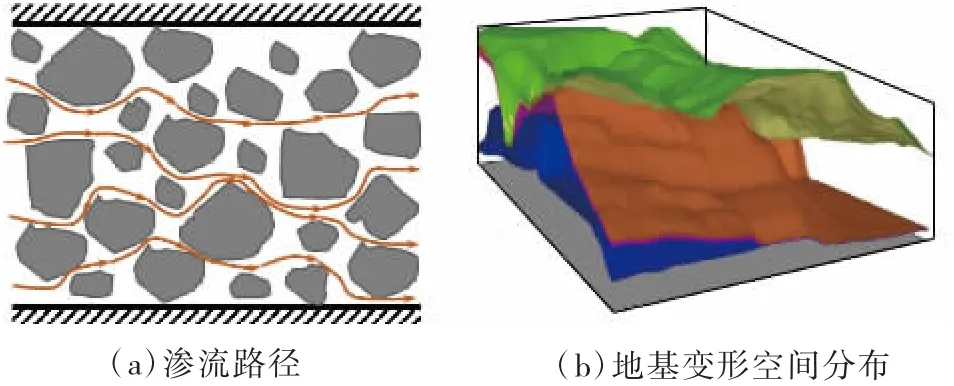
图5 地下水渗流及其对地基沉降影响图示

可见，实际工程中地下水渗透特征、渗流形成的地下水位分布状态、地下水位变化引起的地层附加变形空间分布等十分复杂。同时，其分布形态取决于地层的水力学特性及其分布的基本特征。在实际工程中，无法获得精确的相关参数和函数关系。为建立潮汐渗透水位线，作以下假定：

（1）地层可处理为具有平均渗透系数的均匀介质。

（2）涨潮与退潮海水具有相同的渗流特性。

（3）大潮和低潮呈稳定周期性变化且每个周期的最大潮位差不变。

在高低潮位差形成的水头压力作用下，海水将通过砂性地层的渗透作用向水池施工区域渗透，影响地下水位，以及井点降水水位，形成随海洋潮汐变化的动态地下水位分布曲面和附加地基变形，从而影响水池结构的受力及其抗渗性能。迄今，研究表明，砂性地层的渗透系数如表1 所列。

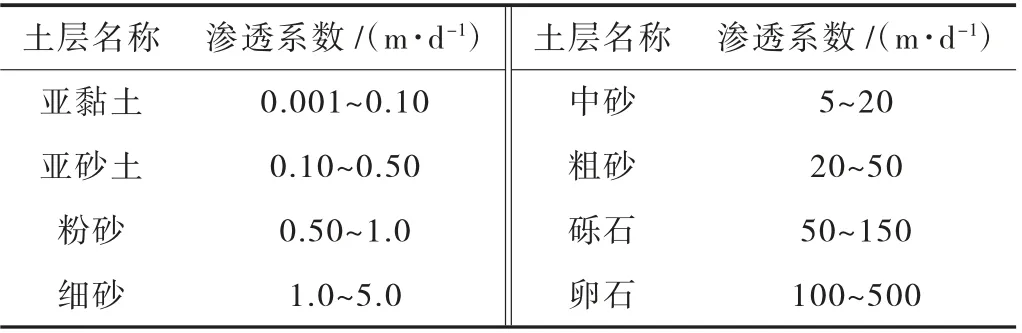
表1 砂性地层渗透系数参考值一览表

根据地层的渗透系数，水在地层中渗流具有一个时间过程，其长短与土体的深流系数密切相关。不同渗透系数的复合地层体系，其渗流过程及任意时刻的地下水位分布十分复杂。

对于海水潮汐渗透问题，涉及到潮流的涨退和叠加问题。退潮时，水位下降形成下降水位线；涨潮时，水位上升形成上升水位线。由于渗透的时间依存性，地层内尚未完全消退的水量在下一波涨潮时必然会产生叠加，形成叠加水位曲面。

假定高低潮位基本不变，在一定地层渗透条件下，低潮位和高潮位将对应着一定渗透条件的地层水位曲面。考虑海岸比较平直、开阔，为便于计算，将海岸线简化处理为直线的竖直渗透面。

根据地下水渗透流动水力坡降特性，建立低潮位及高潮位时地层中水位分布函数如式（4）所示。低潮位渗流水位线方程为：

式中：H为最大潮位差；h0为低潮位与正常地层中水头落差。

由式（4）可得高潮位引起地层上浮位移的表达式（5）。

以上海白龙港工程为例，按上述函数关系作工程区域海水潮汐变化引起地下水位变化、地层附加位移分布如图6 所示。

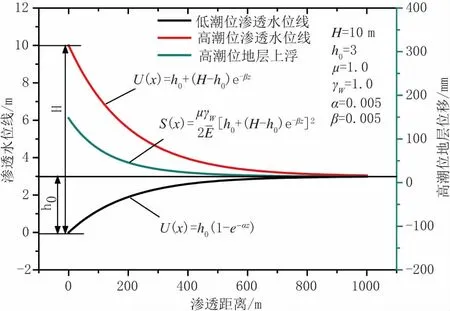
图6 海岸潮汐引起地下水位及地基附加位移图

式（5）对应的曲率半径表达式为：

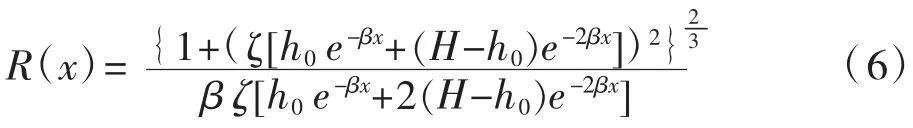
式（6）是一个单调增函数，变化区间为[R（0），+∞），即[115 720，+∞）。假设工程区域地层的渗透特性相同（差异可以忽略不计），海岸潮汐渗透引起地基变形的曲率半径可采用式（6）计算获得。

3 地基变形特征对水池结构应力峰值影响

根据工程特点，基坑开挖见底并浇筑混凝土，土体开挖卸载引起的坑底地基瞬态弹性位移及混凝土结构自重引起的地基变形在混凝土未凝固前已经完成，这两部分位移对水池结构受力影响可以忽略不计。计算中仅考虑混凝土初凝后地基变形状态及其几何特征对结构受力状态及其致裂风险的影响。因此，其力学问题可以抽象为非规则弹性板的变形应力问题。

3.1 地基变形状态一般化函数

引发地基非均匀沉降的原因主要有基坑开挖卸载、地下水位变化、基础加固等。这些因素对地基沉降的作用各自独立，不具有耦合作用和相关性。假定地基沉降为小变形状态，上述因素引发的地基沉降位移适用叠加原理。考虑：（1）基坑开挖卸载位移分布为椭圆抛物面；（2）人工降水引发地基变形呈平行于降水井轴线方向的抛物面分布；（3）地下渗透引发的地基变形呈指数函数分布。综合因素影响下地基变形曲面的一般化形式为指数函数与椭圆抛物面函数的叠加函数，如式（7）所示。

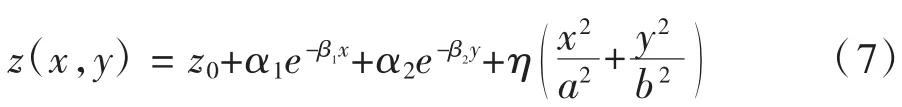
式中：｛α1，α2，β1，β2，η｝为待定系数；a，b分别为椭圆的长轴和短轴。根据现场监测结果即可建立相应的椭圆抛物面函数，用于计算结构应力。

3.2 地基变形引起的结构应力

考虑水池混凝土结构与土体接触面间满足变形协调条件，取模型板（梁）的半高为Hs、混凝土弹性模量为Ec，地基变形引起混凝土结构弯曲曲率半径为R（z）。按设计要求，混凝土结构服役过程处于弹性变形状态。根据结构力学理论，任意截面上的最大正应力为：

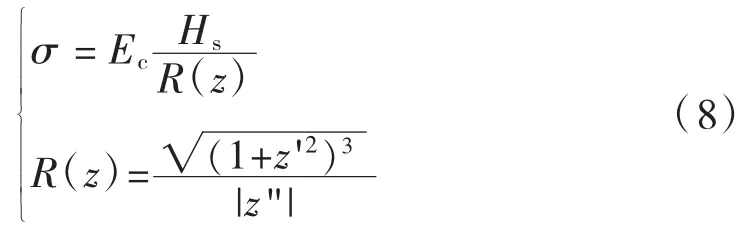
由式（8）可见，当混凝土结构公称高度Hs确定的情况下，决定混凝土结构任意截面上最大应力的参数包括混凝土弹性模量Ec（不同养护龄期变化）和截面上结构曲率半径R（z）。在给定混凝土龄期和结构几何尺寸前提下，结构上最大正应力发生在曲率半径最小的截面外侧。

考虑不同养护龄期混凝土弹性模量、水池结构高度（底板厚度），模拟地基变形最小曲率半径，根据式（8）即可计算对应地基变形条件下水池结构（池周边及底板）最大应力。

参照白龙港水池工程，取结构弯曲高度10 m（对应于水池四周墙体结构）和0.8 m，分别计算对应于前述模拟地基沉降最小曲率半径的结构应力，并与数值模拟计算结果汇总比较如图7 所示。

图7 中的曲线为混凝土弹性模量Ec={10，15，20，25，30，35}MPa 条件下根据弹性结构弯曲应力计算公式（8）计算的对应于混凝土结构养护期T={1，3，7，14，28}结构应力。实心散点是采用地基沉降最小曲率半径和混凝土结构各龄期对应的弹性模量，按式（8）计算的结果。空心散点为数值计算获得的对应于相同点位、相同曲率半径、相同龄期弹性模量条件下的计算结果。

图7（a）显示：（1）三种条件下的计算结果总体吻合，同一曲率半径条件下，计算结果基本位于混凝土弹性模量[20，35] MPa 对应区间内；（2）随结构变形曲率半径的减小，弯曲正应力显著增大。

图7（b）显示：（1）与图7（a）结果比较，由于底板厚度较小（约为水池边墙结构的1/12），理论计算结果几乎等比例减小；（2）数值模拟计算所得水池底板结构正应力明显大于相同参数和边界条件下的理论计算结果。究其原因，数值计算中水池底板上面布置有高度4～5 m 的隔板，很大程度上提高了结构实际高度从而提高了抗弯刚度，从而数值模拟结果大于理论计算结果。

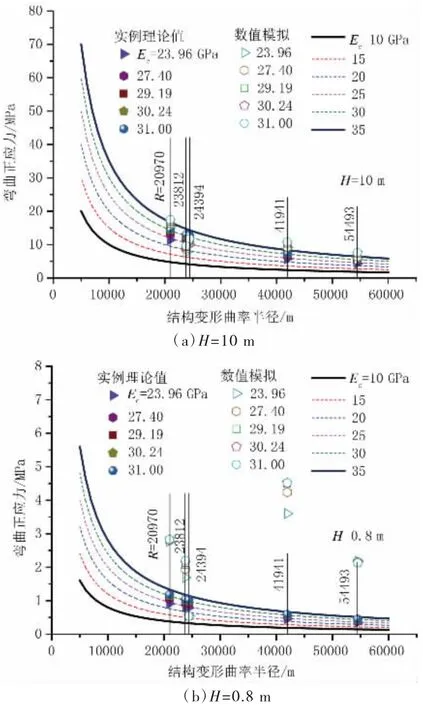
图7 结构弯曲应力随变形曲率半径变化曲线图

综上，地基差异沉降对初龄大面积混凝土结构抗拉稳定性及裂纹的产生、扩展存在较大影响，高度较大的结构更容易产生拉应力超限。尤其，水池结构隔板连接处，因结构刚度突变而形成极高的应力集中，使结构局部应力超限，引发破裂或微裂纹萌生，对水池结构抗渗性能形成不良影响。

4 实例分析

以白龙港污水处理厂提标改造工程为例，地基土体具有分布不均匀、地下水位受地表水源及近海潮汐影响、地下水位分布不均匀等不良工程地质和复杂水文地质条件影响，根据工程地质资料，取各土层的物理力学参数如表2 所列。

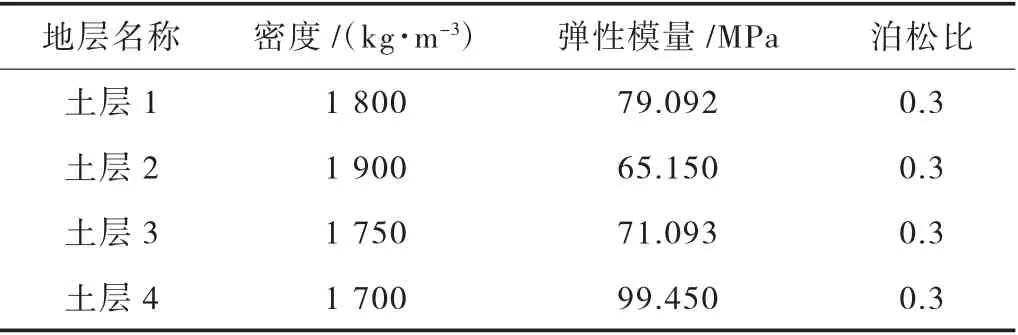
表2 土体力学参数表

假定水池结构与土体之间不产生竖向位移不连续，参考工程现场地基沉降监测结果，建立结构变形曲面函数如式（9）所列。

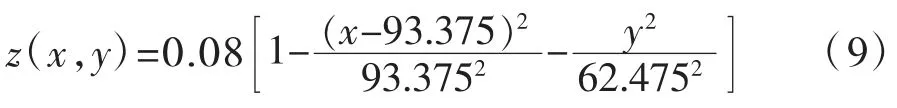
由式（9）得到水池结构最小曲率半径如表3 所示。

表3 水池结构曲率半径最小值一览表 单位：m

当地基产生椭圆抛物面隆起，不同结构拉压应力峰值及其随混凝土龄期变化如图8 所示。

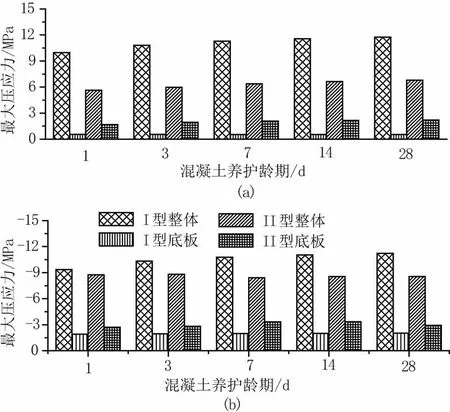
图8 水池结构应力峰值随龄期变化柱状图

图8 结果显示：（1）水池四周墙体混凝土结构拉压正应力均显著大于底板应力值，反映了结构截面高度对弯曲正应力的影响；（2）结构最大拉应力和最大压应力分别沿水池墙体的长度方向，水池四周墙体附加应力显著大于地板结构的峰值应力。

综上所述：（1）结构截面高越大，地基变形弯曲应力越大；（2）结构高度一定且无刚度突变条件下，地基变形曲率变化梯度越显著，弯曲附加应力越大；（3）结构最大张拉应力方向总是沿着结构弯曲变形方向，考虑到混凝土结构抗拉强度低的特性，工程设计中应加强相应部位的布筋设计，提高其抗拉强度从而降低水池结构断裂损伤风险。应力随混凝土养护龄期无明显变化，主要原因是表征结构抗弯刚度特性的混凝土弹性模量随龄期变化不大，但由于初龄混凝土强度较低，极易产生破坏或局部断裂损伤，应引起工程设计高度注意。

5 结 论

根据污水处理池结构特点，建立了地基井点管降水、开挖与桩基础、滨海潮汐地下水渗透影响下地基变形特性及基本变形方程及多因素综合影响下地基变形的统一函数表达式。结果表明：

（1）工程区域人工降水、海岸潮汐等地下土体渗透可能引起地基变形、结构受力的不良影响。

（2）地基沉降模式及其沉降量对上部混凝土结构受力将产生直接影响，沉降变形曲率半径越小，结构产生的附加变形应力越大，造成结构裂纹扩展、抗渗性能弱化的风险越高。

（3）混凝土结构高度越高，对地基弯曲变形的反应越敏感。同时，水池四周结构与隔板结构连接处由于抗弯刚度突变，应力集中程度较高，导致局部应力状态超过结构抗拉强度。

（4）群桩基础可以有效控制地层上浮位移、缓和地基变形曲面形式和曲率半径，从而有效改善上部结构的变形附加应力状态，降低大面积混凝土结构破裂和渗漏风险。