基于格子Boltzmann方法的潜堤上波浪破碎数值模拟
王艺之,韩新宇,董 胜
(中国海洋大学工程学院,山东 青岛 266100)
引 言
近海海域的波浪,在行进中遇到潜堤时会发生剧烈破碎,随后产生波浪增水,形成波生流以及低频波运动。这些水动力过程会影响泥沙输运、潜堤稳定,甚至引起生物栖息地的变化,因此有必要对波浪在潜堤上破碎的情况进行全面的研究。
自19世纪50年代起,有学者针对潜堤上的波浪变形进行了观察及试验[1-5]。研究结果表明,陡坡与缓坡上的波浪变形非常相似,两者的差异主要是波浪破碎的强度和位置。在陡坡上,水深沿程迅速变化,波浪剧烈破碎并产生一段狭窄的破波带,水流可以看作是间歇性的强向岸射流后紧跟着缓慢的向海回流。与此同时,针对潜堤上的波浪传播问题,Symonds等[6]基于对自然礁上波浪的观测以及对其能谱的分析,提出入射波的强度与淹没水深有关;Hearn[7]研究了波浪驱动流在珊瑚礁上的流体动力学及其对礁体的冲刷;Gourlay和Colleter[8]利用明渠理论推导了礁顶流速与入射波条件、淹没水深、堤顶物理特征的关系;Massel和Gourlay[9]提出,假设波和流的时间与空间尺度分离,与辐射应力模型相结合的缓坡方程也适用于研究此类课题。
波浪在潜堤上破碎的数值模拟的关键,在于如何准确对复杂自由表面的变形进行建模。传统的数值模拟方法是从宏观得到微分方程,对该微分方程进行离散化计算并求解,只关心微分方程的形式与结果。而格子Boltzmann方法(LBM)并不是对方程直接求解,其基本思想是从介观动力学出发,将流体离散成介观粒子,按照符合物理规律的演化机制计算粒子系统,观察流场的宏观变化。该方法在宏观上连续,微观上离散,且边界条件易处理,适合大规模的粘性流场计算[10]。
国内最早由朱照宣[11]对LBM的前身格子气自动机方法进行了总结,并提出了一些应用方向;胡守信[12]于1989年在朱照宣[11]和U.Frisch[13]等的基础上研究了直管道中绕平板平面流动的格子气仿真,并于1997年与施卫平共同研究了用LBM模拟无粘性浅水长波方程[14]是国内较早对于LBM及其应用的研究。随后,LBM不断发展,在三维风场[15]、悬浮颗粒运动[16]、明渠水流模拟[17]等方面均得到了广泛应用。
本文探讨LBM模型求解波浪在潜堤上破碎的适用性与准确性。数值建模时,采用推波板造波,并利用斜坡进行消波,构造了二维的数值水槽。分别对高水位和低水位条件下的自由液面高度、波高的空间分布以及斜坡上波浪的增水进行了模拟,并将模拟结果与Wen等[18]的物理试验数据进行了对比,此外还对不同工况下的波浪透射与反射系数进行了计算,所得结果对潜堤结构设计有参考价值。
1 LBM数值模型
目前,LBM已经逐渐成为解决流体流动方程的重要方法。该方法由元胞自动机、格子气自动机模型结合Boltzmann方程发展而来。由于将格子类方法对速度、时间、空间的离散方式与Boltzmann方程的碰撞演化机制相结合,兼具二者的优势。
1.1 控制方程
采用BGK碰撞机制的Boltzmann方程表示如下:
(1)
式中,f=f(x,ξ,t)表示单个粒子的分布函数;ξ表示微观速度;λ表示与碰撞有关的松弛时间;feq表示Boltzmann-Maxwellian平衡分布函数,该函数计算公式表示如下:
(2)
式中,D表示空间维数;ρ,u,T分别表示宏观密度、速度、温度。
将Boltzmann方程对时间进行离散,记沿特征线ξ的时间导数为:
(3)
把式(1)写为关于时间的全微分形式,即:
(4)
对上式进行推导和泰勒展开,忽略高阶无穷小项,记无量纲的松弛时间为τ=λ/Δt,可得对时间的离散结果如下:
(5)
在此基础上,记{eα}为微观速度ξ离散后的速度集合,则得对速度的离散结果为:
(6)
此即BGK逼近下的Boltzmann方程。
对于式(2)表示的分布函数,将其对速度进行泰勒展开至u2并截断高阶项,可得格子Boltzmann模型中的平衡分布函数为:
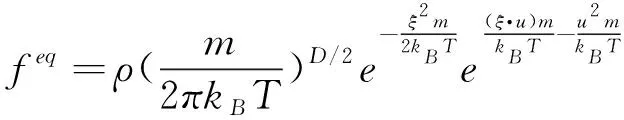
(7)
(8)
可以看出,选定离散速度{eα}后,只要再确定权系数{ωα}就可确定具体的平衡分布函数。
对于n维空间中m个离散速度的情况钱跃竑提出DnQm系列模型,并随LBM的发展不断扩充,其中二维问题中最常用的就是D2Q9,也是本文模拟中所应用的离散速度模型。该模型下的格子速度、权函数、当地声速如下:
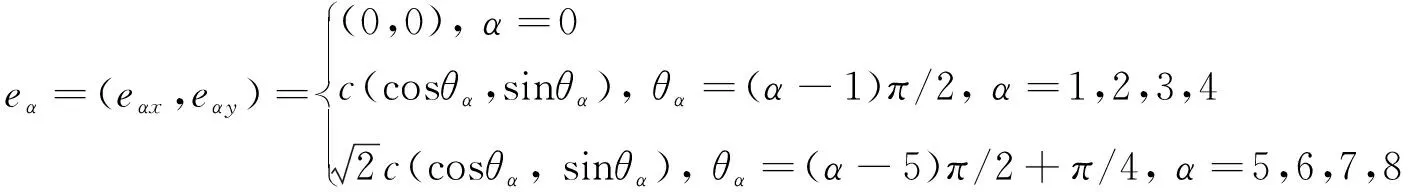
(9)
(10)
在该模型下通过多尺度展开可近似得到不可压缩的N-S方程:

(11)
1.2 湍流模型
湍流模型采用Wall-Adapting Local Eddy-viscosity(WALE)模型,此模型对近壁面和远壁面、层流和紊流都具有良好的特性[19]。该模型可以表示如下:
(12)
式中的系数定义如下:
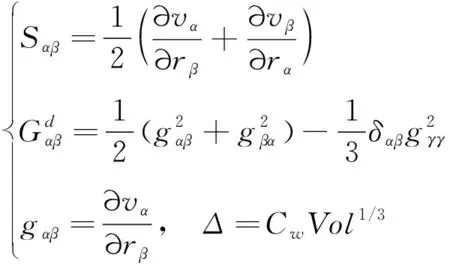
(13)
式中,WALE常数Cw通常取0.2。
1.3 边界条件
本文中应用壁面函数如式(14)所示,同时考虑了曲率和压力梯度的影响,能够较准确的解决湍流边界层的问题[19]:
(14)
式中,y+表示距离墙壁的法向距离;uτ表示表面摩擦速度;τw表示湍流壁面剪切应力;U表示距离墙壁给定距离处的速度。具体定义如下:

(15)
2 数值模拟
数值模型设置如图1所示。水槽长度由入射波长决定。水槽中放置潜堤模型,其陡坡坡度为1:1,坡后平台长8.6 m,高1.8 m。在水槽起始端设置一推板,考虑减少推波板造成的二次反射,将推波板到潜堤的距离设为5.0L(L代表入射波波长);在尾端设置消浪斜坡,坡度为1:10。水槽初始水深设置为d= 1.8+hr,其中hr代表潜堤的淹没水深。

图1 数值水槽示意图
沿数值水槽共布置13个波高测点,它们的相对位置如图1所示。G1—G3位于深水区,G4—G6位于陡坡区,G7—G13位于水平平台区。坐标原点位于坡脚,传感器的坐标如表1所示。

表1 波高仪坐标
考虑到计算精度以及计算效率,本文整体选择4.0 cm的粒子间距,仅在自由表面以及潜堤附近使用粒子自适应方法细化至2.0 cm,示意图如图2所示。模拟时长选取50 s。

图2 自适应粒子细化示意图
3 基于数值结果的分析和讨论
3.1 自由液面高度与试验数据的对比
模拟自由液面高度时共设计两个工况,波高均为0.20 m,周期均为1.75 s,淹没水深分别为0.10 m(高水位)和0.02 m(低水位)。模拟结果如图3和图4所示。对比中用到试验数据以及试验图片来自Wen的论文[18]。
图3给出了两个工况下试验值和LBM计算值的对比结果。可以看出,计算值和试验值吻合良好。说明该模型可以较为准确的模拟波浪在潜堤上的传播过程。通过潜堤平台上的测点结果,可以看到波浪在潜堤上传播的非线性特征,波峰较陡,波谷较缓。由于潜堤的阻碍作用,平台上的波高明显减小。
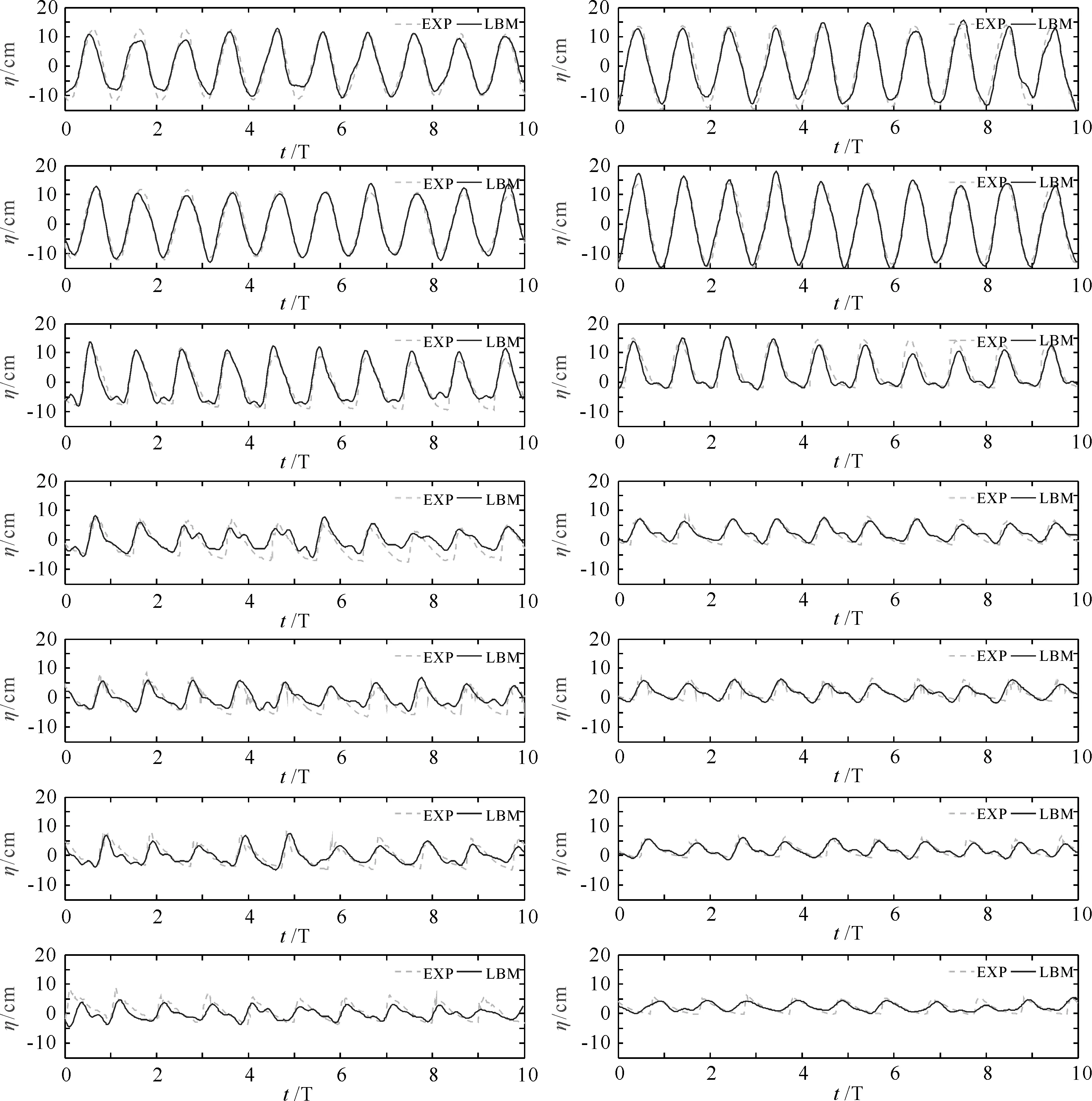
图3 试验结果与LBM模拟结果对比
图4是低水位下波浪与潜堤相互作用过程的自由表面的演变过程,左侧为试验图,右侧为数模图。通过试验和数值模拟可以看出,由于潜堤导致波面升高,随后波浪在靠近斜坡的平台处发生破碎。如图4所示,当t=0.0T时,波浪到达潜堤并开始破碎;当t=0.25T时,崩破波在水平平台传播时,波浪表面开始出现液体飞溅;当t=0.5T和t=0.75T时,已经破碎的波浪继续沿平台传播,与此同时,陡坡与平台的交接处会发生轻微的回流。

图4 瞬时波面对比(低水位)
3.2 波高的空间分布
模拟自由液面高度时,增加1.5 s、2.0 s两种周期,共组合出6种工况进行数值模拟。波高空间分布的试验与模拟对比情况如图5所示,数值模拟沿程波高变化曲线由Akima插值得到,插值节点横坐标与试验结果相同,均为沿程测点的横坐标,纵坐标为模拟结果在该测点位置的波高。从图中可以看出,模拟结果与试验基本吻合,波高随着波浪的传播方向整体呈逐渐衰减的趋势。由于大部分的入射波能量从陡坡反射回深水区,因此在潜堤前可以观察到局部驻波。此外,波浪在潜堤上的破碎导致波能消散,使得波高在潜堤上也迅速衰减。
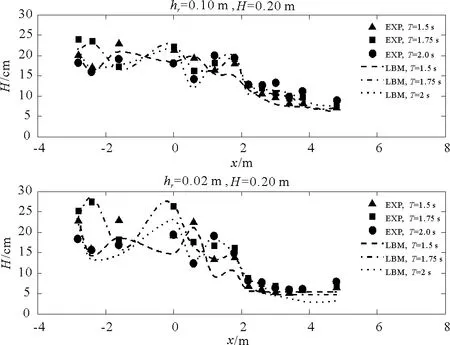
图5 波高在潜堤上的空间分布
3.3 反射系数
图6表示潜堤在不同工况下的反射系数与入射波周期的关系。在潜堤堤脚前1倍入射波长与1.2倍入射波长的位置分别设置一个测点,根据这两个测点处的波高时程变化可以计算得出每个工况的反射系数如表2所示。由图6可以看出,当堤上水深为0.10 m时,潜堤反射系数随入射波周期增大而逐渐增大,且周期与反射系数近似成正比;当堤上水深为0.02 m时,反射系数随入射波周期的增加成先增加后减小的趋势。两种水位的反射系数都在入射波周期为1.5 s时最小,且入射波周期相同的情况下,低水位工况下潜堤的反射系数要比高水位工况的更大。综上所述,潜堤在低水位工况下具有较好的消浪效果。由于本文涉及的工况下潜堤透射系数过小,可以忽略,故本文不对该潜堤的透射系数进行研究。

图6 反射系数变化趋势
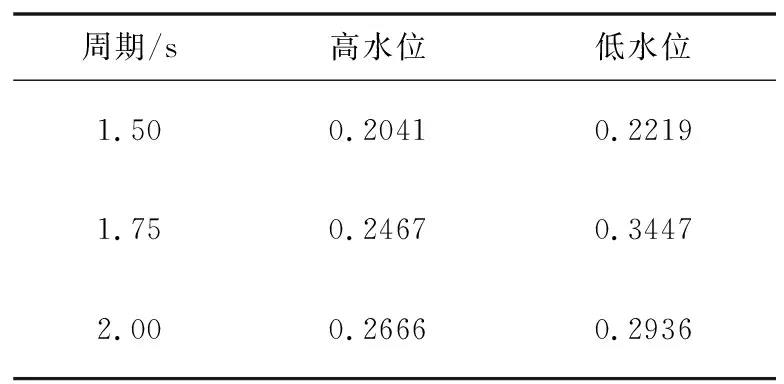
表2 各工况反射系数
4 结论
基于LBM,本文对规则波与潜堤的相互作用进行了研究,建立二维波浪水槽对其进行数值模拟。通过模拟值和试验值进行对比分析,结论如下:
(1)基于LBM方法可以较好的模拟规则波与潜堤相互作用过程中的波浪破碎和液体飞溅等非线性现象,传播过程中的波高与试验吻合良好。
(2)通过对沿程波高进行分析,波高整体呈衰减趋势。在波浪传播到靠近斜坡的平台附近,由于波浪反射和破碎,波高迅速衰减。
(3)在相同波高的情况下,高水位反射系数随周期的增大而增大,低水位反射系数随周期的增大先增大后减小。

