莱州湾岸线变迁对渤海潮波影响的数值研究
朱金龙,朱淑香,张翠敏,徐艳东,魏 潇,孙 伟*,孙贵芹,刘 宁
(1. 山东省海洋资源与环境研究院,山东省海洋生态修复重点实验室,山东 烟台 264006;2. 青岛衡立环境技术研究院有限公司,山东 青岛 266400;3. 烟台市福山区尚德中学,山东 烟台 265500)
引 言
海湾为凹入陆地明显的水曲,在特定的水沙动力条件下,海湾沿岸常发育有粉砂淤泥质海岸,该类型海岸的岸线比较平直,岸坡极缓、滩涂宽广,加之具有优越地理区位和丰富的自然资源,是围填海活动较为适宜的区域。随着海岸带经济的快速发展,人类对土地的需求持续高涨,利用滩涂围填成为人类扩展生存发展空间,缓解土地供求矛盾的有效途径[1-2]。长期的滩涂围填不仅侵占了重要的湿地资源,直接改变了原始岸滩的几何形态,同时也引起了周边海域潮差、分潮振幅和潮汐性质等潮波系统的改变,进而影响滩涂的演变趋势[3-5]。东中国海区沿岸滩涂面积宽广,该区域潮波系统研究始于上个世纪三十年代[6],早期手段主要为潮汐调和分析和数值推算[7-8];随着计算机技术及应用的快速发展,对潮波系统的形成机制、主要分潮分布和潮波系统演变等进行了模拟研究[9-12];后期随着数值计算精度的提高,调和分析得到的分潮数量更多[13-14];近期则更多关注人类活动对潮波系统的影响[1,15-17]。此类研究对于海岸带开发管理、海岸工程建设和生态环境保护具有重要意义。
莱州湾位于山东省渤海南部,和渤海湾、辽东湾并称为渤海三大海湾。湾口东起屺姆岛高角,西至黄河新入海口[18-19]。截至到2000年,湾口宽101.6 km,海岸线长445.8 km,海湾面积6895.7 km2,居山东海湾之冠。莱州湾东部为沙质海岸,西部是现代黄河三角洲,湾顶为粉砂淤泥质海岸。湾周沿岸滩涂多广阔,湾内水深变化不大,最大水深位于海湾东北屺姆岛高角附近,水深可达22 m,大部分水深在10 m以内。莱州湾水浅泥沙多,建港条件很不理想,尤其是海湾的西南部滩宽坡缓,缺乏深水岸线,该处港口布置多采用双堤环抱的平面形式,如潍坊港和广利港,且将堤头延伸到含沙量较低的深水区,以尽量减少进港泥沙数量,从而减小港口回淤量。为了满足建港的深水条件,需向海一侧大规模填海造地,使得海岸线持续向海推进,港口的发展也带动了周边围海养殖和盐业用海活动,围填海面积的持续增加,势必引起渤海潮波系统的改变。针对渤海潮波系统的研究,过去主要模拟了其现代分布特征[13,20-21],从黄河口演变角度对比分析了20世纪40年间的潮波系统变化[22]。近期虽有研究涉及岸线地形变化对渤海潮波系统的影响[15,23-24],但鲜有渤海潮波系统对莱州湾岸线变迁响应的报道。本文利用遥感影像和海图资料,选择莱州湾作为研究区域,通过潮波数学模型计算,分析渤海潮波系统对莱州湾岸线变迁的响应,旨在为渤海潮波系统的变化机制、蓝色海湾整治行动和渤海综合治理攻坚战提供科学依据,并为研究渤海潮波系统演变提供典型案例和参考。
1 资料和方法
1.1 数据来源和处理
莱州湾自20世纪80年代以来,海湾岸线和形态变化逐渐趋于复杂,尤其是2000年以后,沿岸滩涂经历了大规模围填且开发利用强度极大,根据已有的研究结果统计,2002—2015年莱州湾岸线长度的增加占近半个世纪海湾岸线增加值的53%[19]。因此,文中重点关注2000年以后的莱州湾岸线变迁对渤海潮波系统的影响。岸线数据分别提取自2000年和2020年莱州湾历史遥感影像,渤海及黄海北部其他区域的岸线数据保持不变。2000年的岸线资料提取自美国陆地卫星Landsat-5 TM,空间分辨率为30 m;2020年的岸线资料提取自中国高分卫星GF-1,空间分辨率为2.0 m。黄海北部及渤海的水深资料取自航保部2006年出版的编号为10011海图及搜集到的近岸海域水深测量资料。渤海是一个近似封闭的内海,沿岸滩宽水浅,平均水深为18 m,北隍城岛北部的老铁山水道最深,水深可达86 m(图1)。
1.2 潮波数学模型
本文二维潮波模型的控制方程为沿水深积分的N—S方程[25],控制方程的空间离散采用单元中心有限体积法,时间积分采用显示欧拉格式[26]。模型运行时间为2019年1月1日至2019年12月31日,时长为1年。对潮波结果采用最小二乘法进行调和分析,计算各分潮的调和常数,进而作出分潮同潮图、潮汐类型分布图和最大可能潮差分布图。
1.2.1 定解条件
模型范围的选取以研究区域未影响开边界处的进出潮量为准,经反复调试确定模型的计算区域是自江苏淮河口—韩国灵光的连线以及岸线所围成的黄海及渤海海域(图1)。由于风和河流入海径流对潮波的影响很小,因而模型中没有考虑河流入海径流、风以及风吹流的影响[17]。针对岸线曲折和地形复杂特点,模型采用边界拟合较好的非结构三角形网格,网格东西最大跨度约617 km,南北最大跨度约760 km,网格数为137 229个,网格节点数为72 723个,最大网格面积3080 m2。
模型的初始条件:采用前期水深和流速模拟结果的“热起动”方式。边界条件:垂直于陆地边界的法向速度为零;随涨、落潮交替出现的潮滩,采用“干、湿”动边界技术[27],其中湿水深为0.1 m,淹没水深为0.05 m,干水深为0.005 m;开边界水位驱动来自于Topex8.0全球潮汐预报模型[28],是由全球十个主要天文分潮(日分潮:S1,K1,O1,P1,Q1;半日分潮:M2,S2,K2,N2;浅水分潮:M4)组成,分潮数据空间精度为0.125°×0.125°。
1.2.2 模型验证
模型的底床糙率由曼宁系数确定,曼宁系数随水深h取值为0.015+0.01/h[29];水平涡流粘度采用Smagorinsky公式计算[30],Smagorinsky系数Cs取值为0.28;变动时间步长取值介于0.01~120 s;科氏力根据模型所在区域的地理纬度进行计算。
潮波计算结果与黄渤海沿岸26个验潮站(图1)的调和常数进行比较,M2分潮振幅和迟角的绝对误差分别小于4.32 cm和6.32°,K1分潮振幅和迟角的绝对误差分别小于2.12 cm和5.64°。M2和K1分潮振幅、迟角分布与已有的研究结果基本一致[10,24],其中M2分潮在辽东湾西南侧和渤海湾东南侧各形成一个绕无潮点按逆时针方向旋转的驻波系统,K1分潮在渤海海峡附近形成一个绕无潮点按逆时针方向旋转的驻波系统(图3~图4)。本文验证是以前研究成果基础上的继续与完善[31],文中选取与岸线年份相近的实测水文资料进行验证,各站位验证结果表明(表1),除了个别点和个别时刻外,模型计算的潮位过程与现场实测值基本一致,其中高、低潮位的最大绝对误差不超过10 cm,高、低潮时的相位最大绝对误差不超过15 min,模型的验证精度符合有关数值模拟技术规程的要求[32],说明模型采用的计算参数合理,能够较好的模拟渤海的潮波系统。

表1 潮位过程验证
2 结果与讨论
2.1 莱州湾几何形态变化
本文莱州湾几何形态变化从岸线长度、海湾面积和海湾重心三个方面分析。在二维几何空间中,海湾重心的位移方向、路径和距离能够反映海湾形态变化的基本特征。海湾重心坐标(x,y)、重心位移距离L计算公式[33]:
(1)
(2)
式中:xi,yi(i= 1,2,…,n)为海湾平面离散点坐标;xj,yj为j时相的海湾重心坐标;xk,yk为k时相的海湾重心坐标。
自21世纪以来,莱州湾几何形态受自然变迁和人类活动影响变化显著(图2)。岸线的自然淤进和蚀退主要位于黄河口附近,由于河口改道断流缺少沙源补给,老黄河口岸线持续向陆侵蚀后退,而新黄河口岸线则由于长期的沙源供给不断向海淤进。黄河口以外的海湾岸线主要受人类用海活动影响,普遍出现了背陆向海曲折运动,人工岸线长度急剧增长,海湾面积逐年缩减,2000—2020年20年间,莱州湾面积减少了8.02%,海湾岸线增长了77.65%。海湾沿岸开发利用活动长期以围填海为主,尤其是海湾西南部岸线变化最为剧烈,由此导致海湾重心向东北向方移动了2.21 km,港口用海、围海养殖和盐业用海为主的围填海活动是导致海湾形态变化的主要原因。

图2 莱州湾岸线与重心变化Fig.2 Change of coastline and centroid in Laizhou Bay
2.2 渤海潮波系统整体变化
东中国海区潮汐性质以半日潮为主,因此文中潮波选取半日分潮M2为主要研究对象,同时涉及到日分潮K1。黄海潮波经由渤海海峡进入渤海,继续向西传播过程中,受到渤海湾和辽东湾的阻挡而形成反射波,在入射波和反射波的相互作用下形成驻波,由于地转偏向力的作用驻波波节线消失,最终形成了波峰线绕无潮点按逆时针方向旋转的潮波系统[34]。以2020年分潮振幅为例,对于M2分潮而言(图3),无潮点分别位于黄河口和秦皇岛附近海域,分潮振幅最大值位于辽东湾湾顶,其值可达1.3 m,渤海湾湾顶次之,振幅值接近1.1 m,莱州湾分潮振幅最小,振幅值不足0.5 m,海湾以外海域振幅介于0.2~0.6 m;对于K1分潮而言(图4),其无潮点位于渤海海峡偏南部,极值分布与M2分潮振幅相似,分潮振幅最大值位于辽东湾湾顶,其值可达0.42 m,渤海湾湾顶次之,振幅值接近0.37 m,莱州湾分潮振幅最小,振幅值不足0.28 m,海湾以外海域振幅介于0.05~0.25 m。
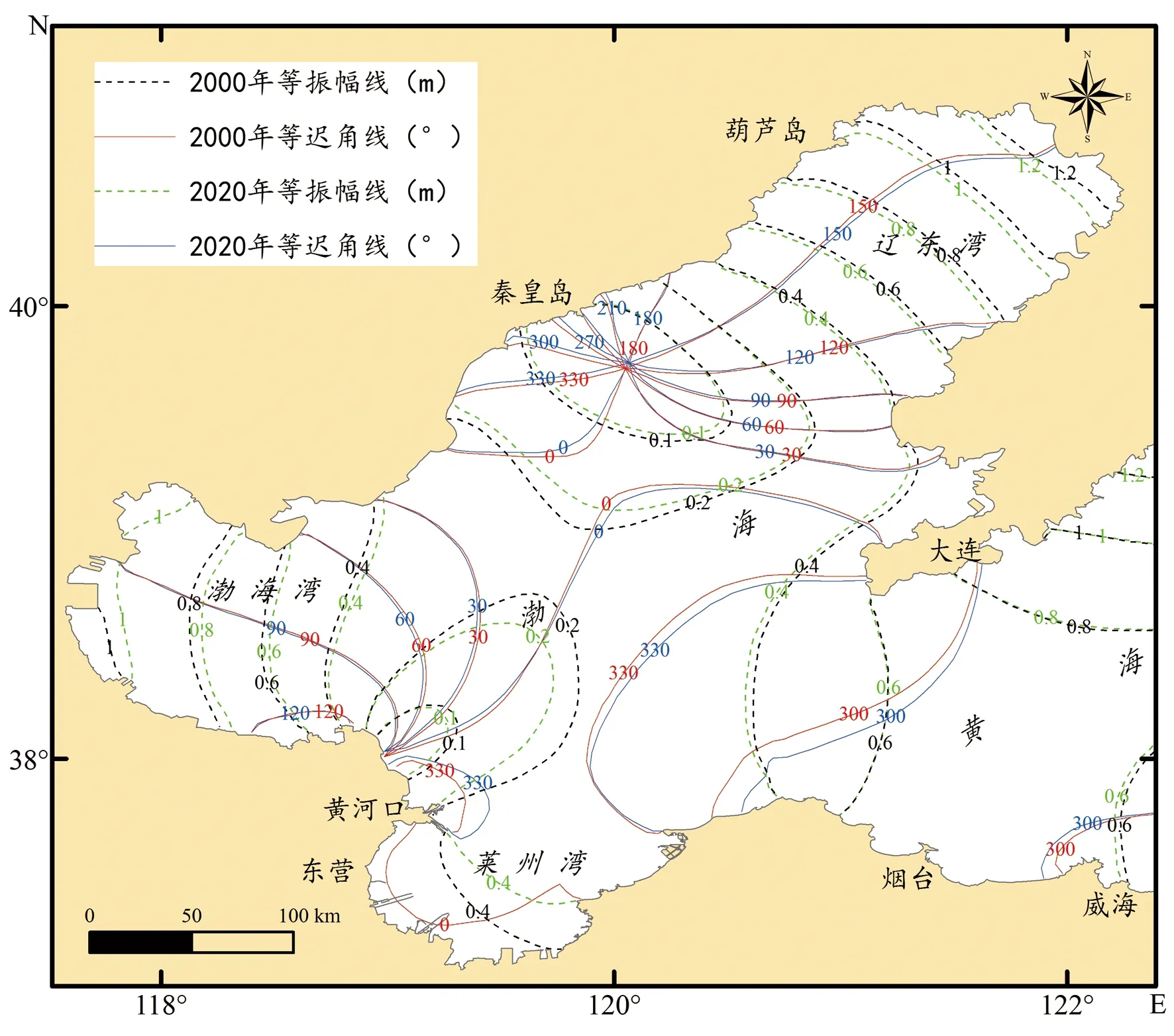
图3 M2分潮同潮图
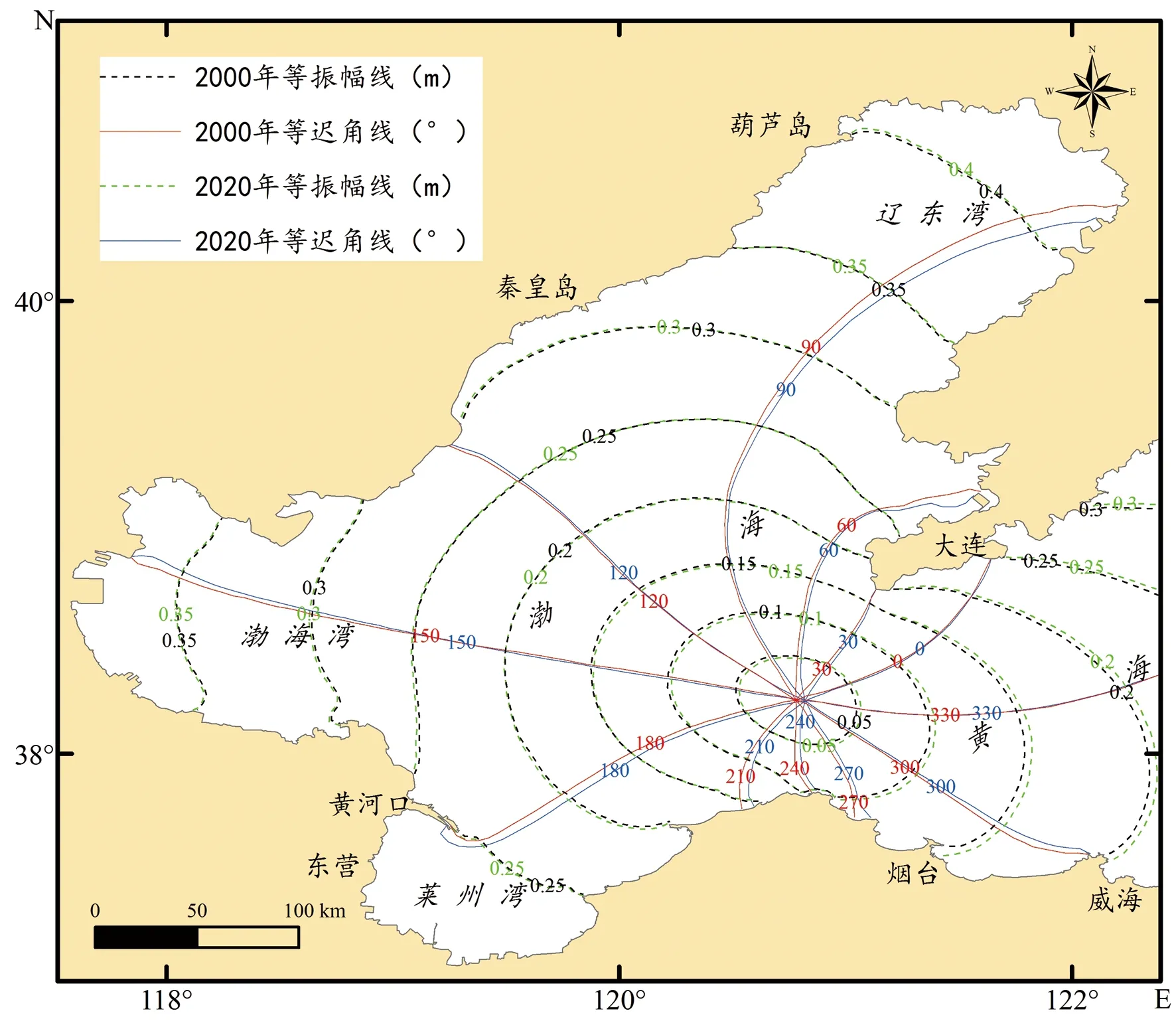
图4 K1分潮同潮图Fig.4 Co-tidal charts for K1 constituent tide
根据潮波原理由潮能分布角度分析,滩涂区潮波能量分布受底摩擦和水平扩散影响,涨潮时滩涂储存能量,落潮时滩涂释放能量,且存储于滩涂区的潮波能量远高于因底摩擦等在滩涂损耗的能量[35]。随着围填海开发活动的进行,20年间莱州湾滩涂面积不断减少,由于岸线变迁并未影响数值计算开边界处的进出潮量,因此原先存储于滩涂区的那部分潮波能量,随着滩涂的消失将在滩涂以外的海区重新分布,由此使得整个受影响海区分潮振幅增大、无潮点背离莱州湾等一系列潮波系统变化。从而导致黄河口附近M2分潮无潮点向西北移动1.4 km,秦皇岛附近M2分潮无潮点向东北移动1.7 km,渤海海峡偏南部的K1分潮无潮点向东移动2.1 km。由此可见,秦皇岛附近M2分潮无潮点受围填海的影响要大于黄河口附近M2分潮无潮点所受的影响,这主要是由于新黄河口持续向海发育,潮波传播受到河口岸线的阻碍而损耗掉一部分潮波能量,使得黄河口附近M2分潮无潮点移动距离小于秦皇岛附近M2分潮无潮点移动距离。与秦皇岛附近海域相比,渤海海峡距离莱州湾较近,因此K1分潮无潮点移动距离要大于秦皇岛附近M2分潮无潮点移动距离。受莱州湾岸线变迁的影响,2000—2020年20年间,渤海M2分潮振幅整体呈现增大趋势,其中莱州湾、渤海湾和辽东湾M2分潮振幅是自湾口向湾顶逐渐增大,辽东湾和渤海湾M2分潮振幅增加最大值位于湾顶,其值可达4.2 cm,围填海发生区域的莱州湾振幅变化尤为显著,增加最大值可达6.5 cm,海湾以外海域M2分潮振幅增大值小于4.1 cm;K1分潮振幅变化主要发生在渤海海峡以东的海域,海峡以东K1分潮等振幅线整体向东移动,振幅值变化不足1 cm,其他海区K1分潮振幅变化很小,也由此说明了岸线变迁对潮波的影响主要为半日分潮。
2.3 潮汐性质和最大可能潮差变化
根据各海区潮位随时空变化情况将潮汐性质分为规则半日潮、不规则半日潮、规则日潮和不规则日潮四种类型。潮汐类型判别依据下式:
F=(HK1+HO1)/HM2
(3)
式中:HK1为日分潮K1的振幅;HO1为日分潮O1的振幅;HM2为半日分潮M2的振幅。
潮汐类型判别标准:0 < F ≤ 0.5为规则半日潮;0.5 < F ≤ 2.0为不规则半日潮;2.0 < F ≤ 4.0为不规则全日潮;F > 4.0为规则全日潮。
根据研究海域潮汐性质,依据公式(5)和公式(6)计算最大可能潮差,取两者中的最大值,最大可能潮差计算公式[36]:
mptr=max(mptr1,mptr2)
(4)
mptr1=2(1.68HK1+1.46HO1+HM2+HS2)
(5)
mptr2=2(1.29HM2+1.23HS2+HK1+HO1)
(6)
渤海潮汐以不规则半日潮为主(图5),由于M2分潮驻波波腹和K1分潮驻波波节出现在渤海海峡,因此该海区为规则半日潮类型;而黄河口外和秦皇岛附近海域为K1分潮波驻波波腹和M2分潮驻波波节所在区域,因此该海区为不规则全日潮和规则全日潮类型。受莱州湾围填海影响,黄河口外和秦皇岛附近海域不规则全日潮和规则全日潮所占海区范围呈现减小趋势,通过章节2.2的分析,这可能是由于莱州湾围填海导致该海区M2分潮振幅增大,而日分潮振幅基本不变,导致公式(3)的比值减小,从而造成不规则全日潮和规则全日潮范围缩小。
渤海最大可能潮差最大值位于辽东湾湾顶,以2020年最大可能潮差为例,其值可达5.71 m,渤海湾湾顶次之,最大可能潮差值接近4.79 m,莱州湾内最大可能潮差最小,最大可能潮差值不足2.9 m,渤海海湾以外海域最大可能潮差介于2~3 m。
莱州湾岸线变迁引起的渤海最大可能潮差变化和M2分潮振幅变化趋势基本一致(图6),莱州湾、渤海湾和辽东湾最大可能潮差是自湾口向湾顶逐渐增大,最大可能潮差增加最大值位于莱州湾湾顶,其值可达17.5 cm,辽东湾湾顶次之,增加最大值接近11 cm,渤海湾湾顶最小,增加最大值不足9.5 cm,海湾以外海域最大可能潮差增大值小于9 cm。莱州湾围填海相当于增加了潮波传播阻力,使得进入渤海的潮波势能增加,潮波势能即潮差,由此引起了渤海潮差的增大[1,35]。
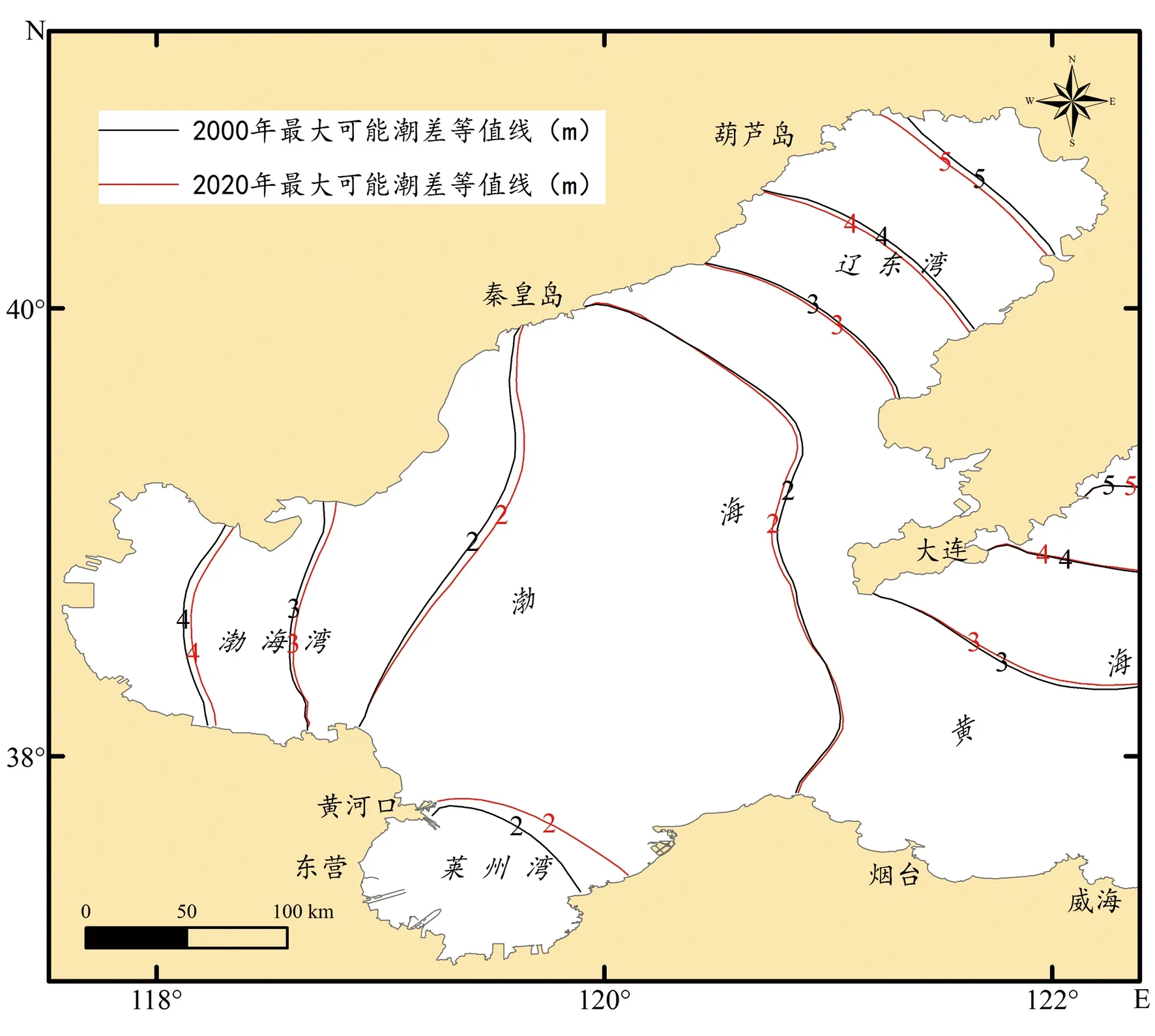
图6 最大可能潮差分布
3 结论
(1)2000年以来,莱州湾几何形态变化显著,海湾面积不断缩减,海岸线持续向海曲折运动,港口用海、围海养殖和盐业用海为主的围填海是引起海湾形态变化的主要原因。2000—2020年20年间,莱州湾面积减少了8.02%,海湾岸线增长了77.65%,尤其是海湾西南部岸线变化最为剧烈,由此导致海湾重心向东北向方移动了2.21 km。
(2)受莱州湾20年间岸线变迁影响,黄河口附近M2分潮无潮点向西北移动了1.4 km,秦皇岛附近M2分潮无潮点向东北移动了1.7 km,渤海海峡偏南部的K1分潮无潮点向东移动了2.1 km;渤海M2分潮振幅整体呈现增大趋势,其中莱州湾振幅增大最为明显,增加最大值可达6.5 cm;K1分潮振幅变化主要发生在渤海海峡东侧,岸线变迁对潮波的影响主要为半日分潮。
(3)渤海潮汐以不规则半日潮为主,部分海区如渤海海峡为规则半日潮类型,黄河口外和秦皇岛附近海域为不规则全日潮和规则全日潮类型。受莱州湾岸线变迁影响,黄河口外和秦皇岛附近海域不规则全日潮和规则全日潮所占海区范围缩小,渤海海域最大可能潮差增大,尤其是围填海发生区域的莱州湾潮差变化最为显著,增加最大值可达17.5 cm。围填海造成的潮差增大使得沿岸低洼区域有被淹没的风险,因此海湾沿岸大规模围填海的实施需要经过全面的科学论证。

