基于门控神经网络的储能电站荷电状态估计研究

宋 洁， 赵雪莹, 2， 朱玉婷， 梁丹曦， 徐桂芝， 邓占锋

(1.全球能源互联网研究院有限公司， 北京 102209； 2.清华大学电机系， 北京 100084)

1 引言

随着中国碳中和、碳达峰目标的提出，以光伏、风电为代表的可再生能源战略地位凸显，电化学储能作为支撑可再生能源发展的关键技术，将迎来行业的蓬勃发展。其中锂离子电池以功率密度、能量密度、循环寿命和自放电率低等优点，成为储能系统的首要选择。其短时供应电力、电力削峰填谷和能源利用率高等特点，成为储能行业的主要能源载体。荷电状态(State Of Charge，SOC)估计作为能量管理系统的关键，其准确估计可以保护电池系统运行安全，防止过充或过放影响电池使用安全及寿命，同时为电池组均衡策略控制提供关键参考。

SOC作为不可直接测量的参数，通常定义为可用容量与参考容量的比值[1]，表征电池的剩余电量。目前，SOC估算方法主要分为4类。安时积分是一种十分传统的SOC估算方法[2,3]，其计算公式源自SOC的定义[4]，具有计算消耗低的优点。但是，安时积分需要一个准确的初始SOC值才能保证SOC估算精度；对电流测量精度的要求较高，否则在长时间的使用中会产生较大的累计误差；而且安时积分没有修正能力，在实际应用中会产生较大的估算误差。

基于开路电压(Open-Circuit Voltage, OCV)的方法估算电池SOC[5]因电池OCV是电池SOC的函数得以实施，不过基于OCV估算SOC在现实中很难应用，这是因为OCV需要电池经过足够长的静置才能测得。同时OCV-SOC的关系受电池循环寿命与温度的影响较大[6]，在复杂的现实情况中难以获得良好的估算条件与结果。

基于模型的方法是建立一个准确的电池模型，模拟电池在复杂工况下的响应[7]，根据模型的公式从而直接或间接地估算电池的SOC。模型可分为电化学模型和等效电路模型。电化学模型基于复杂的偏微分方程[8]，计算量巨大，不适合在线估计。与之对比，等效电路模型则计算量小，是现在主流的使用方法，通过等效电路模型公式在线估算电池的OCV[9]，理想情况下，等效电路模型能准确反映电池在复杂工况的响应。然而，锂电池系统作为一个强耦合与非线性的系统[10]，很难找到一个完美的模型结构能准确等效真实电路，并且在对模型进行参数辨识时也很难找到一组完美的模型参数。通常将基于等效电路模型的方法与扩展卡尔曼滤波(Extend Kalman Filter, EKF)的方法结合使用，然而，EKF使用一阶泰勒展开式对非线性系统近似线性化会带来截断误差，造成估计精度的损失，且基于模型的方法不能考虑温度和老化对电池SOC估计的影响[11]。

与基于模型的方法不同的是，神经网络方法不需要建立电池模型，而把电池看作一个黑箱模型，通过大量的数据，训练出一个能反映观测值如电流、电压、温度与电池SOC非线性映射关系的模型。目前已经有许多神经网络方法估算电池SOC。文献[12,13]使用支持向量机(Support Vector Machine, SVM)估算SOC。然而，支持向量机所需的计算量巨大，并且泛化能力差。文献[14]使用深度神经网络(Deep Neural Networks, DNN)估算SOC，然而SOC估计过程是一个时间序列的问题，DNN忽略了电池SOC与电压电流历史信息的关系。文献[15,16]使用长短期记忆网络(Long Short-Term Memory, LSTM)估算SOC，LSTM虽然能避免循环神经网络(Recurrent Neural Network, RNN)的梯度消失或爆炸的问题，但是LSTM本身的内部参数过多，不方便训练，且增加了过拟合风险[17,18]。

综上所述，针对基于LSTM预测模型的不足，本文提出一种基于门控神经网络(Gated Recurrent Unit,GRU)-Dropout的电池SOC预测方法。首先GRU[19]简化了内部结构，内部参数更少，训练更快，且过拟合风险更小，并消除了RNN因为梯度消失或爆炸的问题[18]；为了提高模型预测的泛化能力，避免模型训练时Dropout[20]正则化对模型进行局部优化；使用Adam[21]优化方法进行模型参数优化；最后通过对该方法进行验证，结果表明本文方法具有良好的估算精度。

2 GRU-Dropout模型

2.1 GRU原理

GRU网络在RNN的基础上引入重置门与更新门，t-1时刻的隐藏层状态(hidden state)不直接参与t时刻隐藏层状态的计算，而是通过重置门与更新门决定参与下一个时间步计算的信息数量。通过修改神经网络中隐藏状态的计算方式，解决当时间步数较大或者时间步数较小时，RNN的梯度容易消失或者爆炸的问题，从而使GRU更好地捕捉时间序列中时间步距离较大的依赖关系。GRU网络的结构如图1所示。

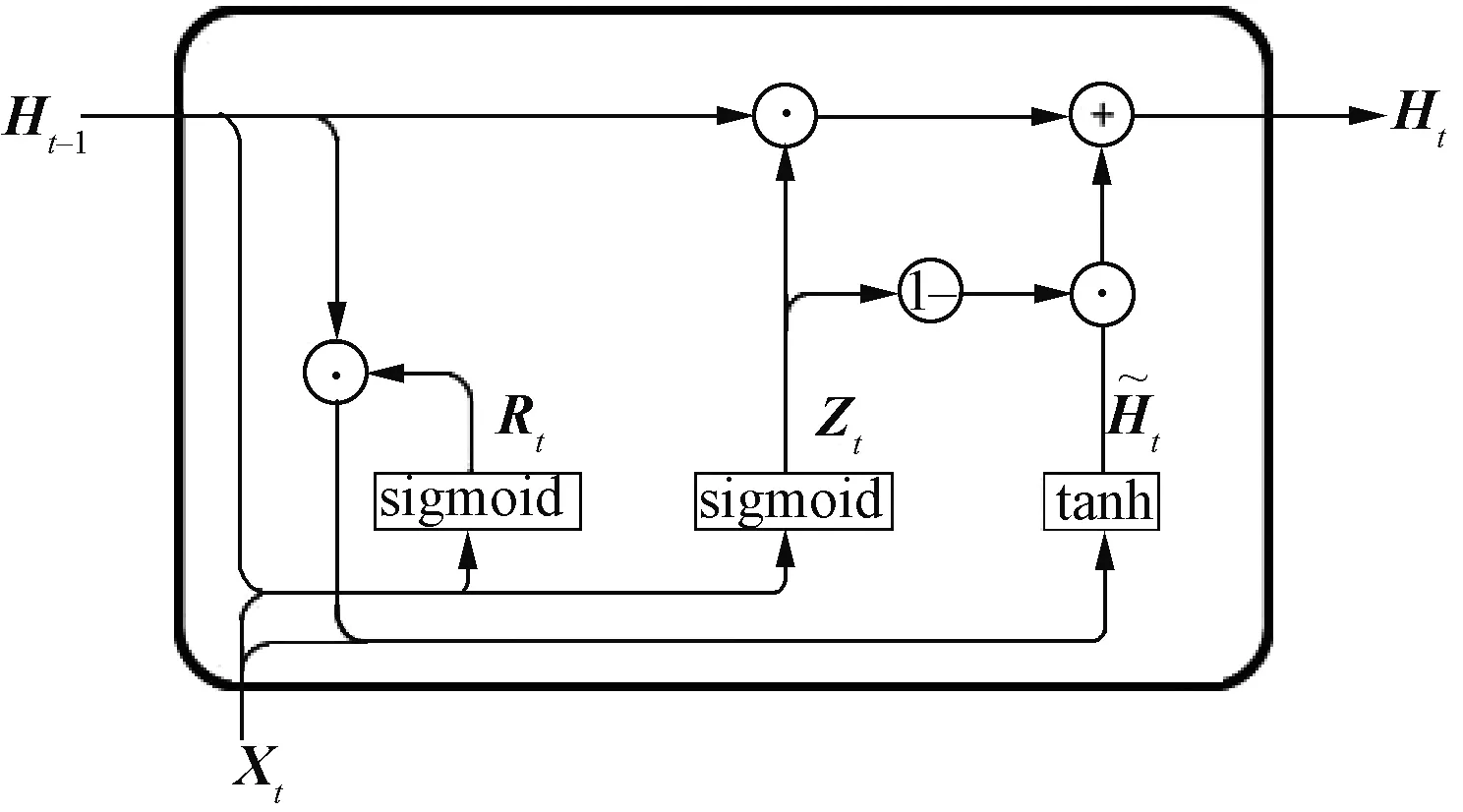
图1 GRU Cell结构Fig.1 GRU Cell structure

在GRU中，首先计算重置门和更新门，计算公式为：

Rt=sigmoid(XtWXR+Ht-1WHR+bR)

(1)

Zt=sigmoid(XtWXZ+Ht-1WHZ+bZ)

(2)

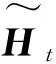
(3)

式中，WXH为输入向量的权重矩阵；bH为候选隐藏层状态的偏置；tanh为激活函数，计算公式为：

(4)

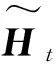
(5)

式中，⊙为按元素乘积。

2.2 Dropout原理

当网络的模型变得很复杂时，权值衰减就很难应对过拟合情况，而Dropout则可以在网络很复杂时抑制过拟合，使模型获得良好的泛化能力。Dropout是一种在学习过程中随机删除神经元的方法。训练前，先预设丢弃概率为p，则每个隐藏层神经元有p的概率被清零，有1-p的概率会除以1-p做数值的缩放。具体来说，随机变量ξi为0和1的概率分别为p和1-p。使用丢弃法时计算新的隐藏单元h′i为：

(6)

由于

E(ξi)=1-p

(7)

因此

(8)

即Dropout不会改变其输入的期望值。Dropout工作原理如图2所示，其中，x为Dropout过程中输入参数，h为Dropout过程中隐藏层参数，o为Dropout过程中输出参数。

图2 Dropout原理示意图Fig.2 Dropout schematic diagram

在测试时，为了得到确定性的结果，不使用Dropout。

2.3 GRU-Dropout的SOC估计

对于SOC估计，电池管理系统(Battery Management System,BMS)测量的电压电流数据是进行SOC估计的关键参数。本文中，使用电压电流作为GRU-Dropout神经网络的输入参数。假设N是数据样本的总数，则网络的输入数据集为X={Xi|i=1,…,N}，其中，第i个输入向量为Xi={ψi,t|t=1,…,T}，向量ψi,t=(Ii,t,Vi,t)表示在(i-1)L+t时刻测量的电压电流值。L是序列长度，也就是输入的窗口大小，输出数据集Y={Yi|i=1,…,N}，其中Yi=SOCi，SOCi表示输入Xi后网络计算出的SOC值。X，Y都是张量数据，其维度分别为(N,L,2)和(N,1,1)。对于输入数据集，其维度的含义为有N个样本，其中每个样本包含L个2维向量,并按时间顺序依次排列。

本文提出的GRU-Dropout神经网络估算SOC的工作流程如图3所示。将样本Xi输入到GRU层，GRU层通过学习输入数据的时间序列关系后输出一个大小为c的向量，其中c为隐藏层的节点数。该向量经过Dropout层后，经过全连接层后计算出Yi=SOCi。为了评估本文提出方法的性能，使用平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)作为误差的评价标准。RMSE表征估计的鲁棒性，MAE表征估计的准确性。

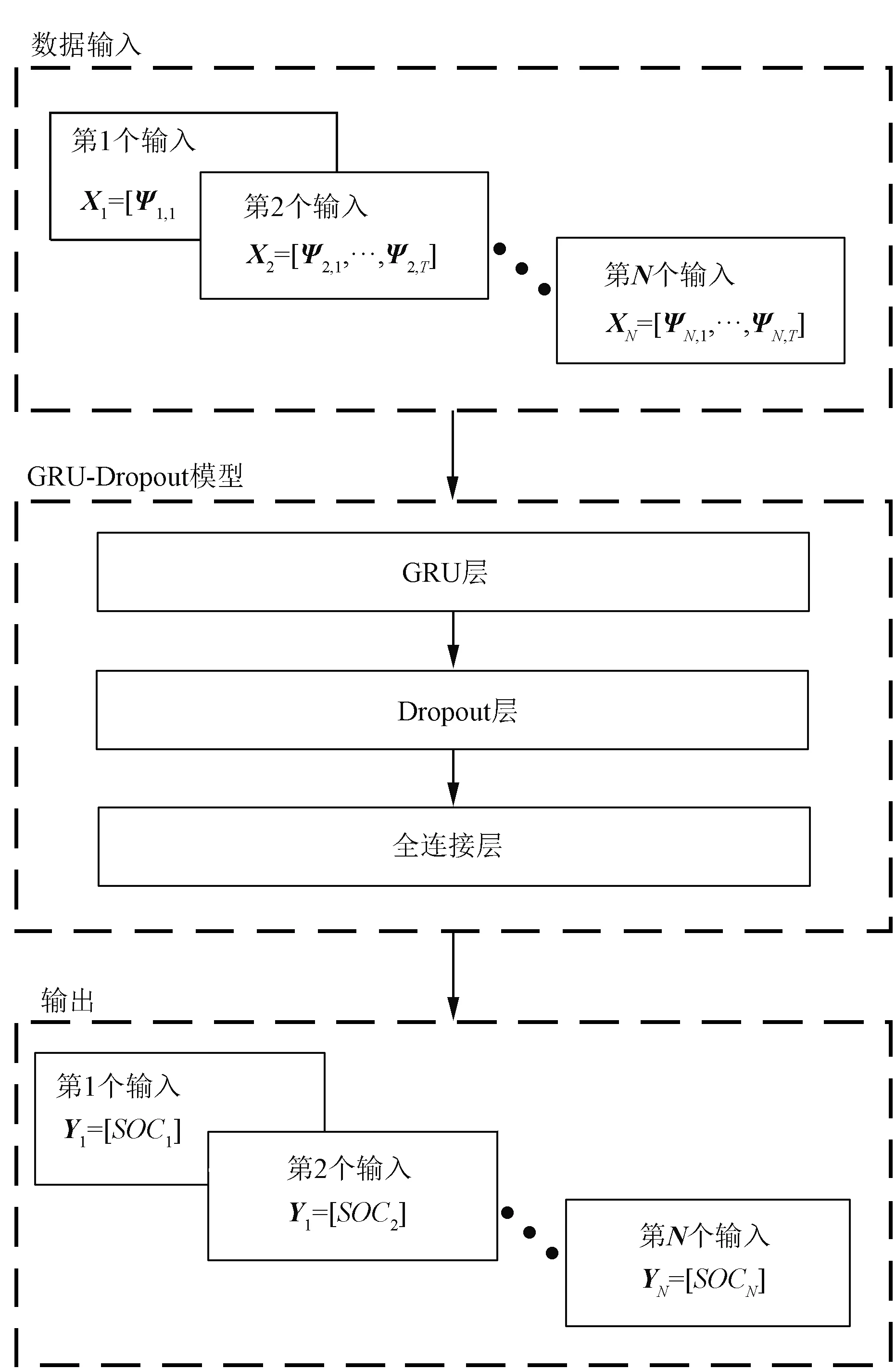
图3 GRU-Dropout的SOC估计流程图Fig.3 Flow chart of GRU-Dropout for SOC estimation

(9)

(10)

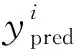
3 数据描述

为了模拟储能系统在复杂工况下的表现，使用模拟动态工况作为储能电池的动态功率需求。实验分为三个阶段：充电工步、放电工步、静置工步。首先，电池以1 C的电流进行恒流充电。当电池电压达到4.2 V时，切换为恒压充电，逐渐降低充电电流，当电流降至0.01 C时停止充电，此时电池视作完全充满电状态。经过2 h的静置后，分别使用模拟动态工况1、工况2、工况3(参考美国环保署的动态工况HWFET，US06及UDDS测试方法)对电池进行放电。放电过程中，当电池电压达到截止电压2.5 V时停止放电。工况的电流电压如图4～图9所示。数据采样间隔为0.1 s。

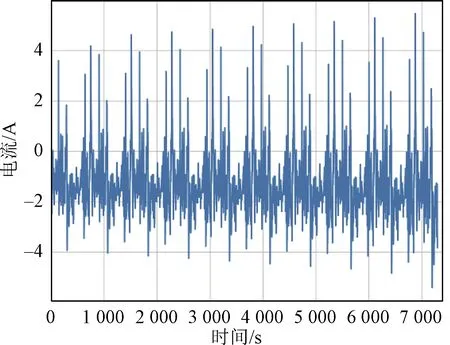
图4 模拟工况1电流Fig.4 Current diagram of working condition 1

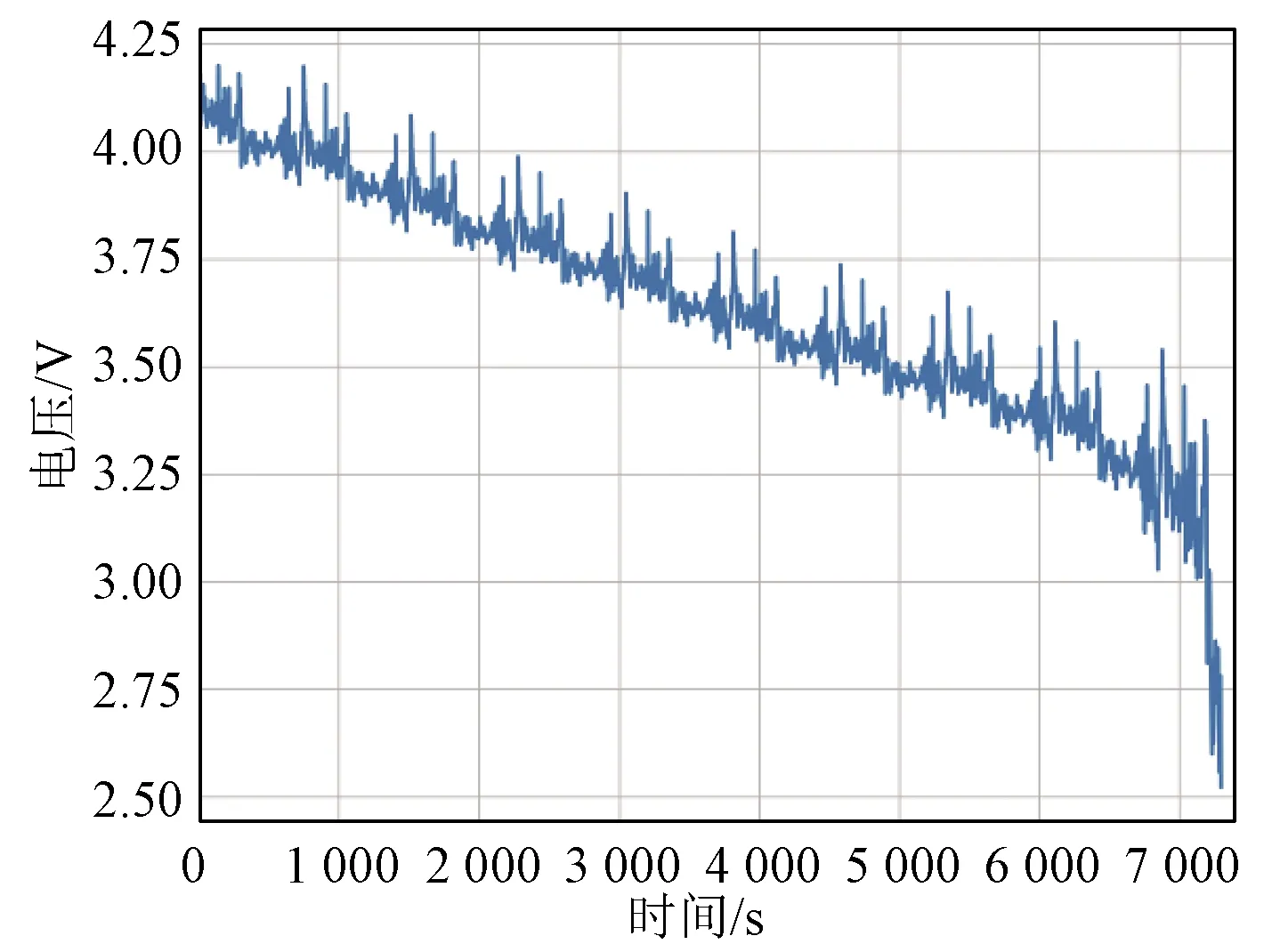
图5 模拟工况1电压Fig.5 Voltage diagram of working condition 1

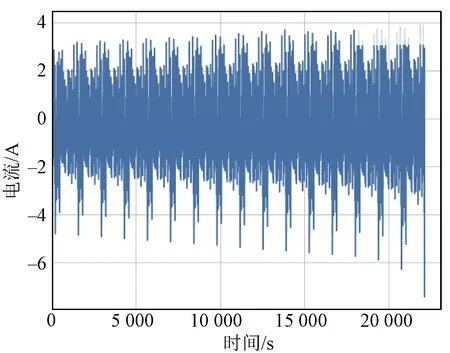
图6 模拟工况2电流Fig.6 Current diagram of working condition 2

图7 模拟工况2电压Fig.7 Voltage diagram of working condition 2

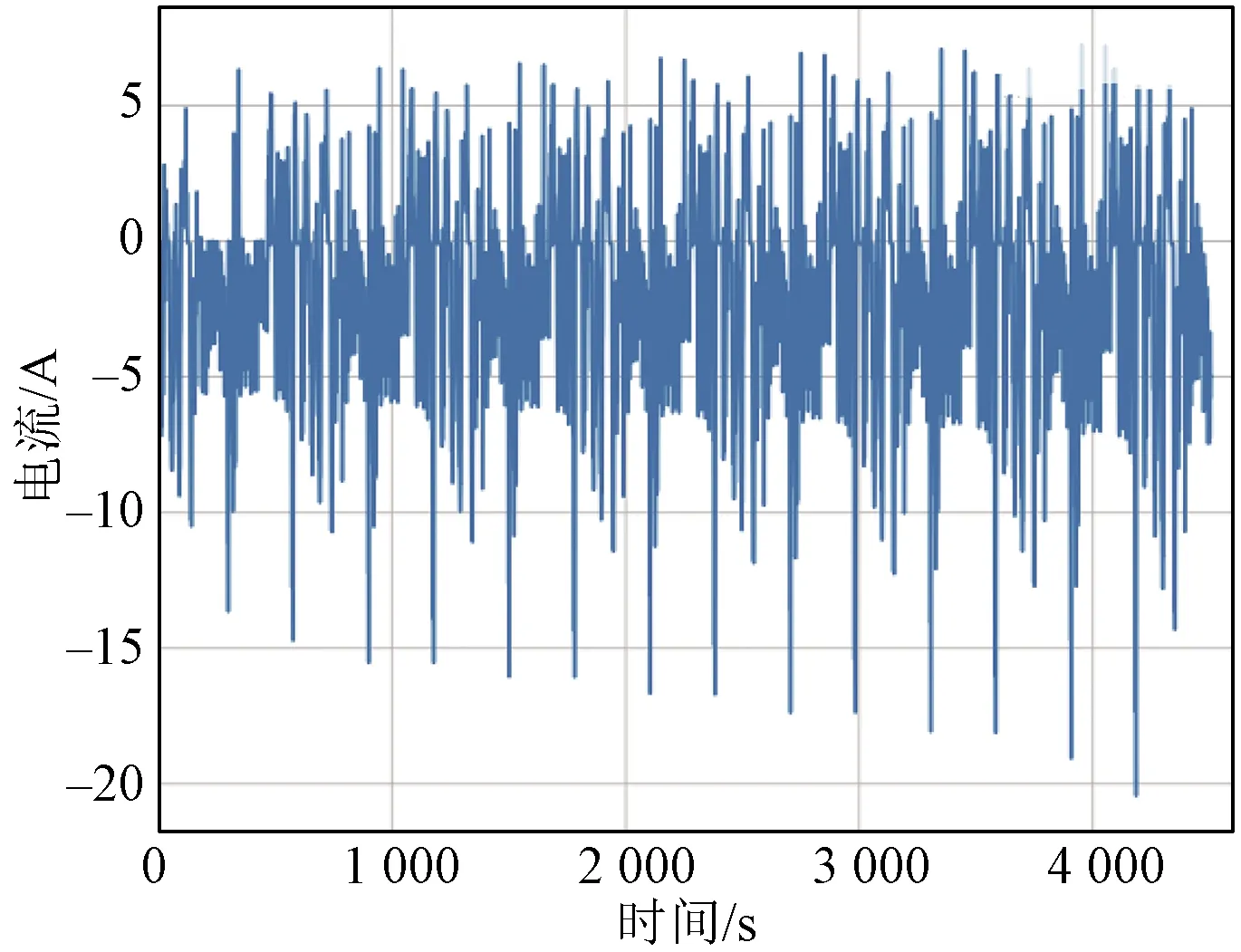
图8 模拟工况3电流Fig.8 Current diagram of working condition 3

图9 模拟工况3电压Fig.9 Voltage diagram of working condition 3

为了加快梯度下降并提升网络的质量，数据集X需要在训练之前进行标准化Xnorm。公式如下：

(11)

式中，Xmax与Xmin分别为X中的最大值与最小值。

当数据经过标准化之后，设置GRU-Dropout的超参数，包括数据长度大小与隐藏层节点数。这些超参数将在实验部分进行讨论。设置好模型的超参数后，使用Adam算法[22]作为优化器对模型进行训练。Dropout的概率设置为0.2。使用模拟工况1和模拟工况2对模型进行训练，经过1 000轮的训练后，批量大小设置为128，激活函数使用Tensorflow框架默认激活函数。使用模拟工况3对模型进行测试并评估精度。对于不同的电池类型，如磷酸铁锂电池，由于电池特性带来实验数据的差异，需要对模型进行重新训练与测试。

4 实验验证

4.1 不同数据长度下的SOC估计

数据序列长度表示输入数据的时间窗口大小，其对SOC的估算有重要的影响。本节讨论不同的数据长度对SOC估计精度的影响。通过分别设置数据长度L=[20,30,40,50]进行训练，并用MAE和RMSE评价估算的精度。模型在不同的数据序列长度下的估算精度见表1。当设置数据序列长度为40时，估算精度最优，其中MAE为1.38%，RMSE为1.66%，如图10所示。当数据序列长度值设置较小时，估算精度相对数据序列长度设置为40的估算精度有所下降。当不断增大数据序列长度值时，估算的精度却没有明显的增加，但是训练所需耗时却明显增加。例如，当数据序列长度为50时，模型的估算精度MAE仅比数据序列长度为40时高一点，RMSE还下降了。综上所述，数据长度不是越大越好，而是应该设置为一个合理的值。故4.2节的实验将L设为40。

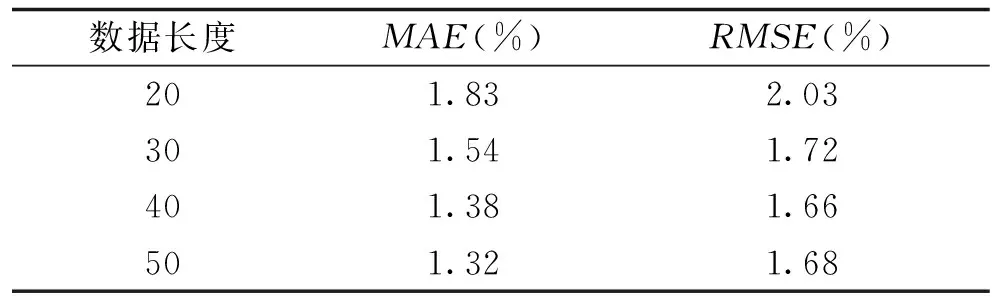
表1 不同数据序列长度的模型误差Tab.1 Model error of different data sequence lengths

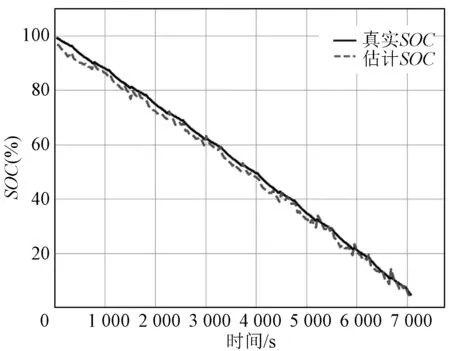
图10 L=40,c=16时的SOC估计Fig.10 SOC estimation at L=40, c=16

4.2 不同隐藏层节点数下的SOC估计

GRU-Dropout节点数是隐藏层状态的宽度。隐藏层的节点数对模型的估算精度有重要的影响。通过设置c=[16,32,64,128]对模型进行训练,然后评估节点数大小对估算精度的影响。c分别为[16,32,64,128]时的SOC估计误差见表2。模型在设置不同的节点数时的模型SOC估计如图11～图13所示。当c为64时，模型的估计精度最优，MAE与RMSE分别为1.38%与1.67%，体现了GRU-Dropout的估计准确性。当隐藏层节点数较小时，如隐藏层节点数为16或32时，估算精度较隐藏层节点数为64时明显降低。当设置隐藏层节点数较大时，会增加网络的过拟合风险。如当设置隐藏层节点数为128时，模型的MAE比隐藏层节点数为64时提升0.18%，但是RMSE却下降了，说明此时已经有过拟合的风险。

表2 不同网络节点数的模型误差Tab.2 Model error of different units

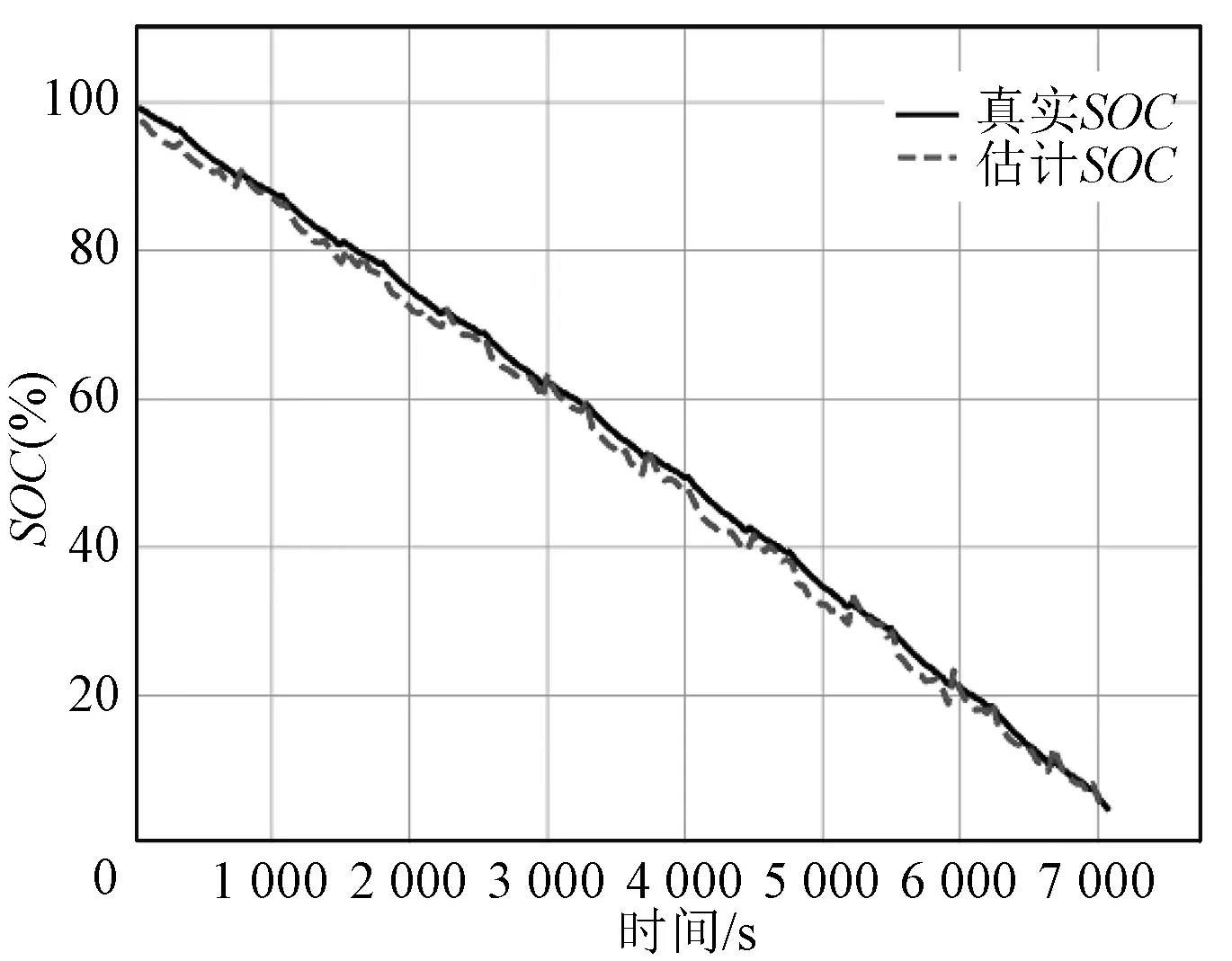
图11 L=40, c=32时的SOC估计Fig.11 SOC estimation at L=40,c=32

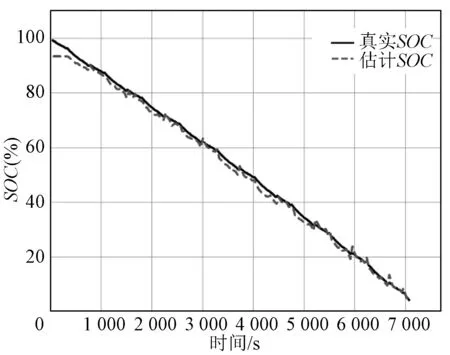
图12 L=40, c=64时的SOC估计Fig.12 SOC estimation at L=40, c=64

图13 L=40, c=128时的SOC估计Fig.13 SOC estimation at L=40,c=128

5 结论

本文提出使用门控单元结合Dropout的GRU-Dropout神经网络估计储能电站荷电状态的方法，通过GRU的拟合能力学习电压电流和温度与SOC的非线性关系。使用Adam算法作为模型的优化器，确保网络的训练速度和稳定性。与传统的方法相比，本文提出的方法不需要建模与参数辨识。与长短期记忆网络相比，GRU具有更小的过拟合风险，内部参数也比LSTM少，降低了计算复杂度。为了验证GRU-Dropout神经网络的估算效果，使用模拟工况1和模拟工况2进行训练，使用模拟工况3电池数据对GRU-Dropout神经网络进行测试。实验表明，本文提出的方法能准确地预测电池的SOC值，最优结果为平均绝对误差1.38%，均方根误差1.66%。