基于改进秃鹰搜索算法的变压器J-A模型参数辨识

莫仕勋， 杨 皓， 蒋坤坪， 梁振燊

(广西大学电气工程学院， 广西 南宁 530004)

1 引言

变压器作为电力系统中的关键设备，其建模方法一直是学者研究的热点，而目前电力系统各类设备的建模趋于精细化，对变压器的建模要求也越来越高[1，2]。

变压器建模的一个关键点在于磁滞现象的表示，由于磁滞特性在实际运行中会影响到波形形状，经过傅里叶变换后得出的各次谐波含量都会有很大差异，所以会对变压器保护的二次谐波判据等闭锁条件产生影响，可见，磁滞能否正确且准确地在变压器建模中得以表征，无论对于电力系统稳态暂态的精确计算，还是继电保护的准确整定都有较大影响。

在目前的研究中，磁滞模型也分为多种，而相比于SW(Stoner-Wolhfarth)模型，Preisach模型等[3]，J-A(Jlies-Atherton)磁滞模型具有参数较少、物理意义清晰等优点，在电磁材料磁特性模拟研究中被广泛应用[4]。

J-A模型由代数-微分方程组描述，其中有5个未知参数，未知参数的大小直接决定了磁滞回线的形状，从而影响到变压器模型的精确度[5]。无论是需要利用J-A建模还是在仿真软件中利用带磁滞的变压器，都需要用到这5个参数，而要得到这5个参数，就要通过已有的曲线数据进行参数辨识。

目前，智能算法在优化领域是研究的热点之一，使用智能优化算法对微分方程的参数进行辨识也具有优越性，在磁滞参数辨识领域，模拟退火算法(Simulated Annealing, SA)[6]及遗传算法(Genetic Algorithm,GA)等是较为常用的智能算法。利用智能优化算法进行参数辨识，或者将智能算法与传统的方法结合[7]具有更高的精度，所以得到了更广泛的应用。

虽然这些算法能基本辨识出所需的参数，但是精度依然不高，并且往往需要迭代多次，消耗很长时间才能寻找到最优解，也有可能陷入局部最优，精确度和实用性均达不到要求，在此基础上结合传统方法进行改进的文献[7]中算法复杂，步骤较为繁琐。针对这些问题，本文提出了一种改进秃鹰搜索(Bald Eagle Search， BES)算法，以实现对 J-A 磁滞模型参数的快速、精确辨识。该方法将Tent混沌映射、精英反向学习策略与自适应权重融入BES算法，将待求值快速收敛于全局最优值。结合实验数据，使用该算法对 J-A 磁滞模型参数进行辨识，然后基于所得到的参数对磁性材料的磁滞特性进行模拟，并将模拟结果与其他算法的模拟结果及实验结果进行了对比分析。结果表明，使用该算法辨识模型参数时收敛速度更快、辨识精度更高，基于该算法辨识参数的模拟磁滞回线与实测曲线吻合较好，验证了该算法的实用性和有效性。

2 J-A磁滞模型

磁滞模型有Preisach模型、J-A模型及SW模型等，其中由量子理论描述的J-A磁滞模型以其物理意义明确、参数易于获取等优点得到广泛应用[8]，J-A模型中，无磁滞磁化曲线由改进的Langevin函数表示：

(1)

式中，Man为无磁滞磁化强度；He为有效磁场强度；Ms为饱和磁化强度；a为无磁滞磁化曲线的形状参数；He和磁场强度H又有如下关系：

He=H+αM

(2)

式中，α为平均场参数，反应磁畴间的耦合程度；磁化强度M又可分为可逆磁化强度Mrev及不可逆磁化强度Mirr两部分：

M=Mrev+Mirr

(3)

可逆分量Mrev、不可逆分量Mirr与无磁滞磁化强度Man之间存在如下关系：

Mrev=c(Man-Mirr)

(4)

式中，c为磁化因数。

最终根据能量平衡方程可得：

(5)

式中，δ为方向系数，当dH/dt>0时取1，dH/dt<0时取-1；k为牵制系数；μ0为真空磁导率。

式(1)～式(5)即为J-A理论描述的磁滞现象，求出dM/dH后，由式(6)便可求得铁心磁导率μFe：

(6)

由以上分析可知，J-A磁滞模型共包含5个未知参数，分别为Ms，α，a，c，k。对于用于制造变压器铁心的硅钢片，已知的数据往往为此硅钢片的B-H或M-H磁滞回线，若需建模，需使用的是5个未知参数。如此问题便转化为微分方程组的参数辨识问题，以实测值与仿真值的均方根误差Fitness作为适应度函数，表达式如下：

(7)

式中，n为B-H磁滞回线所包含点的个数；g为其中的第g个点；Bmea为硅钢片已知的B-H曲线的磁感应强度；Bcal为通过已知的H数据由J-A模型计算得到的磁感应强度值。式(7)的值越小，说明计算出的点与实际的点越接近，磁滞曲线越吻合。此问题便转化为最小值优化问题，利用优化算法不断优化便能达到最优参数。

3 秃鹰搜索算法

秃鹰主要生活在美洲地区，有出色的视力和观察技能，主要选择鱼作为食物。在捕食猎物时，秃鹰会从各种方面评估狩猎的成本及成功概率，再进行移动与捕捉。其首先根据个体和种群对鲑鱼的集中程度选择搜索空间，向特定区域飞行;其次，在选定的搜索空间内对水面进行搜索，找到合适的猎物后，秃鹰逐渐改变高度，迅速俯冲，成功地从水中捕获鲑鱼等猎物[9]。

马来西亚学者Alsattar 受到秃鹰捕食过程的启发，于2020年提出了一种新型智能算法——秃鹰搜索优化算法, 此算法以上述秃鹰的捕食习惯为基础, 将秃鹰的捕食过程分为三个阶段[10], 数学模型为：

(1)确定搜索区域：秃鹰在栖息地通过判断猎物在各个区域的密度来确定最佳搜寻位置，便于搜索猎物,并通过观察结果来确定位置变更，更新由随机搜索的先验信息Pi,new乘以β来确定。该阶段的数学模型为:

Pi,new=Pbest+β·rand·(Pmean-Pi)

(8)

式中，β为控制位置变化参数，变化区间为(1.5,2)；rand为 (0,1) 间随机数；Pbest为当前秃鹰搜索确定的最佳搜索位置；Pmean为先前搜索结束后秃鹰的平均分布位置；Pi为第i只秃鹰位置。

(2)搜索空间猎物：在上一步选定的搜索区域中，秃鹰呈螺旋形状盘旋飞行，寻找最佳俯冲捕获位置，螺旋飞行数学模型采用极坐标方程表示,位置更新公式如式(9)～式(12)所示:

θ(i)=Pbest+bπ·rand

(9)

r(i)=θ(i)+R·rand

(10)

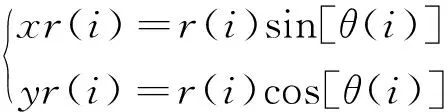
(11)

(12)

式中，θ(i)与r(i)分别为螺旋运动方程的极角与极径；b、R控制螺旋运动轨迹，变化区间分别为(0,5)、(0.5,2)；x(i)与y(i)为极坐标中秃鹰位置。秃鹰位置按式(13)更新：

Pi,new=Pi+x(i)(Pi-Pmean)+y(i)(Pi-Pi+1)

(13)

(3)向猎物发起猛扑：确定猎物位置后，秃鹰从搜索空间的最佳位置快速俯冲飞向目标猎物, 此时种群其他个体也跟着向最佳位置移动并攻击猎物, 这一阶段的运动方程为式(14)～式(16)、式(12)。

θ(i)=bπ·rand

(14)

r(i)=θ(i)

(15)

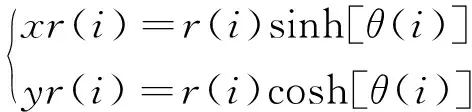
(16)

俯冲中秃鹰位置更新公式如式(17)、式(18)所示：

(17)

Pi,new=rand·Pbest+δx+δy

(18)

式中，c1与c2为秃鹰向最佳与中心位置的运动强度，取值范围均为(1,2)。

根据多个测试函数表明，BES算法具有较强的全局搜索能力, 能够有效地解决各类复杂数值优化问题，因此可以式(7)作为适应度函数，不断寻优，理论上可以得到J-A磁滞模型参数。但同时，标准的BES算法和其他元启发式算法一样，存在收敛速度慢、解的搜索精度相对较低且容易陷入局部最优值的缺点[11]，需要针对这些缺点对算法进行改进。

4 BES算法的改进

4.1 Tent混沌映射

混沌是自然界中的一种现象，智能算法初始化种群时使用rand函数随机生成种群个体，无法保证种群个体分布在各个位置，即无法保证种群的多样性，降低了算法的效率，且更容易陷入局部最优。而采用混沌映射方法可以解决这一问题。在多种混沌映射方法中，Tent混沌映射各方面性能优于其他一些常用混沌映射方法，如Logistic 混沌映射[12]，可以用于产生优化算法的混沌序列[13]。Tent映射结构简单，且映射呈现的结果分布密度比较均匀，具有很好的遍历性，因此本文采用Tent混沌映射增加BES算法的初始种群多样性。

Tent 混沌映射的表达式如式(19)所示：

(19)

式中，sn为第n次运算求出的混沌序列值；are用于调整范围，对are与s的初始值进行调整，就可以得到在不同范围内的按Tent混沌分布的随机值，从而增加BES 算法的初始种群多样性，求出Tent混沌序列后，利用混沌序列对初始种群进行映射，即将式(19)产生序列的集合载波到待求解空间，最终的种群生成公式如式(20)所示：

odim,new=omin+(omax-omin)odim

(20)

式中，dim为混沌序列的维度；odim,new为混沌序列载波到待求解空间后的新值；odim为式(19)产生的混沌序列；omax和omin分别为序列中变量的最大值、最小值。

使用 Tent混沌映射得到的新值xdim,new作为 BES算法初始种群的分布，增加了种群的多样性，提高了BES算法的全局搜索能力。

4.2 精英反向学习

即便BES算法能有不错的效果，也存在一定的局限性[10]，秃鹰选择搜索空间利用上个阶段的可用信息来确定下个搜索区域, 在随机选择另一个搜索区域时, 会依据之前的搜索域来确定相应的邻域进而完成本次秃鹰第一阶段的搜索过程, 因此针对秃鹰选择搜索空间而言, 如果秃鹰群体在上一次的迭代过程陷入了局部最优状态, 那么便无法跳出此局部最优，整个寻优过程便无法更为准确, 即无法在某类特定优化问题中求得最优解, 降低了启发式智能优化算法的最优化效果。

反向学习机制(Opposition-Based Learning，OBL)可以有效增加种群的多样性和质量，目前已被较好地应用于多种算法的改进中[14，15]，反向学习机制首先计算当前解的反向解，然后从当前解和其反向解的种群中选取最优解更新个体。反向学习策略的定义如下：

反向学习的原理为，对于一个解来说，其自身和其反向解总有一个更接近最优解，反向解的引入，可以扩大算法的搜索区域，但是反向学习存在其生成的反向解可能比当前搜索空间更难搜索到最优值的问题，并且对那些原解适应度值大于反向解适应度值的个体，对其进行反向区域的搜索，则相当于在做无用功，而对原解适应度值小于反向解适应度值的个体，对其进行反向区域的搜索价值要高于其领域的开发价值。

针对反向学习的缺点，精英反向学习(Elite Opposition-Based Learning，EOBL)被提出，由前文分析可知，精英个体比普通个体携带更多有效信息，EOBL利用这一特点，通过种群中精英个体形成反向种群，然后从反向种群和当前种群中选取优秀个体构成新的种群[16]，避免了对低价值信息的反复计算及利用，所以相对于反向学习来说，精英反向学习提高了效率。精英反向学习在每次迭代中增加了种群多样性与局部搜索能力，可以有效地避免算法落入局部最优解。

精英反向解的定义如下：

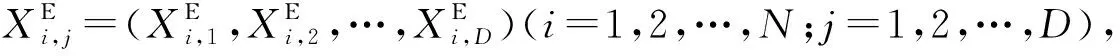
(21)

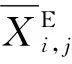
4.3 自适应权重

惯性权重是智能算法改进的重要方法，迭代初期，为了快速达到最优解附近，对全局搜索能力的要求高些；迭代后期，需要对区域进行精细的搜索，所以对局部搜索能力的要求高些。如果按照基础的智能算法，每一步的搜索方式都是一样的，无法达到以上要求，降低了算法的效率。借鉴惯性权重的思想，在秃鹰位置更新方式中继续引入动态权重因子，使其在迭代初期具有较大的值，能够更好地进行全局探索，在迭代后期自适应地减小，从而更好地进行局部搜索，同时提高收敛速度[17]。

自适应权重的公式如式(22)所示：

(22)

式中，t为算法本次迭代的迭代次数；max_iter为算法的最大迭代次数。

改进后的位置更新由式(18)变为式(23)所示：

Pi,new=rand·Pbest+ω(δx+δy)

(23)

经过以上三点改进得到新算法，在此命名为改进秃鹰搜索(Improved Bald Eagle Search，IBES)算法。

5 J-A模型参数辨识及比较

5.1 J-A模型参数辨识流程

根据上文所提算法改进，可得以下具体步骤：

(1)初始化参数，如种群数量、最大迭代次数等，并利用Tent混沌映射初始化秃鹰种群。

(2)结合自适应权重因子计算每只秃鹰的适应度值，找出当前最优适应度值和最差适应度值，以及相对应的位置。

(3)从适应度值较优的个体中，选取部分作为精英个体。

(4)对精英个体求其反向解，计算精英反向解所对应的适应度值及相应的位置。

(6)将反向解对应的适应度与原来的解进行比较与排序，更新出较优的解。

(7)判断是否达到结束条件，若是，则进行下一步，否则跳转步骤(2)。

(8)程序结束，输出最优结果。

J-A模型参数辨识流程图如图1所示。

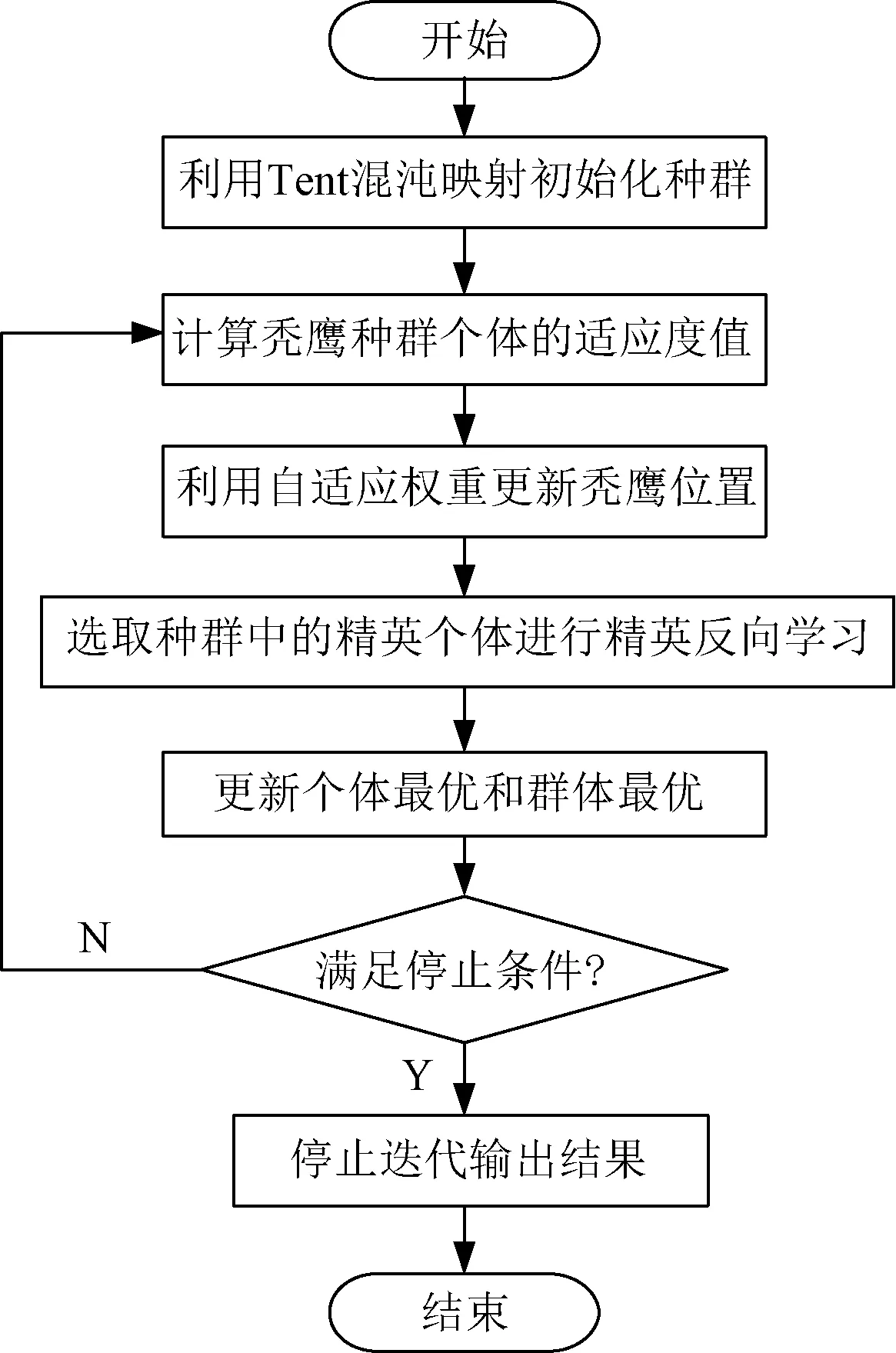
图1 IBES算法流程图Fig.1 IBES algorithm flow chart

5.2 参数辨识及算法的比较

为验证IBES算法在 J-A 磁滞模型参数辨识问题上的正确性与有效性。本文使用文献[5]的参数生成一条仿真曲线作为基准磁滞曲线，包含500个数据点。

SA是J-A模型参数辨识的常用方法，本文采用SA、BES、IBES分别对磁滞回线进行参数辨识并进行对比，IBES和BES种群数量为30，迭代次数为100次，SA算法最大温度为100，最大容忍度为10-8。

本仿真测试环境为：操作系统 Windows 10，CPU为AMD A10-9630P RADEON R5, 2.60 GHz，内存为4 GB，仿真软件为Matlab2018b。

比较智能算法J-A参数辨识主要参考几方面：磁滞曲线吻合程度、迭代次数、迭代时间、最小适应值以及具体辨识出参数的相对误差。

三种方法辨识得到参数计算出的磁滞曲线与待辨识磁滞曲线的对比如图2所示。

图2 各算法辨识参数生成的磁滞回线与基准磁滞回线的对比Fig.2 Hysteresis loops generated by parameters identified by each algorithm as compared with reference hysteresis loops

由图2可见，几种算法所辨识的结果计算出的曲线基本与实际磁滞曲线相吻合。证明了利用IBES算法对J-A模型参数进行辨识的有效性。

三种算法的均方根误差(适应度函数)随迭代次数的变化如图3所示。

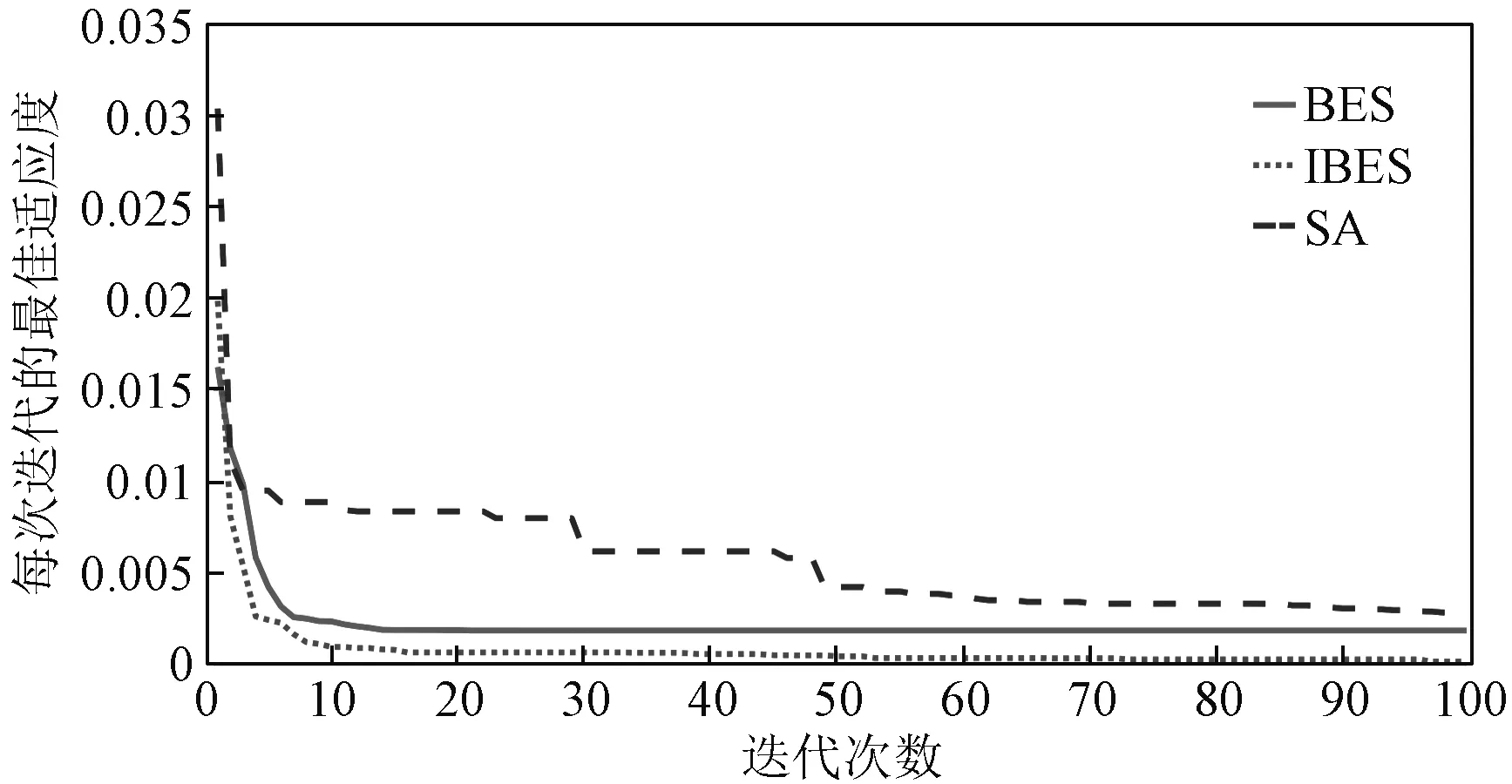
图3 各算法均方根误差随迭代次数的变化Fig.3 Change of root mean square error of each algorithm with number of iterations

由图3可见，SA算法经过多次迭代后依然未收敛至全局最优值，收敛速度最慢。BES算法快速收敛于全局最优值附近，但是从第6代开始收敛速度减慢，在第20代收敛于局部最优值；而IBES算法在10代前收敛速度均高于BES算法，收敛至相同结果附近所用的迭代次数远少于BES和SA，最终得到的适应度值也优于其余两种算法，三种算法的最终均方根误差见表1。

表1 IBES与BES、SA算法辨识结果比较Tab.1 Comparison of identification results between IBES and BES and SA algorithms

由表1可见，根据仿真结果，IBES算法的均方根误差优于SA与BES算法，适应度函数越小，说明曲线对应的点距离越近，即辨识出参数所计算的曲线与实际曲线越吻合，而由于使用IBES算法所辨识参数与理论值较为贴近，所生成的仿真B-H曲线和基准曲线的吻合度较高。

各个算法辨识出的5个参数见表2，参数辨识所花时间见表3。

表2 IBES与BES、SA算法辨识结果比较Tab.2 Comparison of identification results between IBES and BES and SA algorithms

表3 IBES与BES、SA算法辨识耗时比较Tab.3 Comparison of identification time consuming between IBES and BES and SA algorithms

由表2展示的辨识结果可见，SA算法在每个参数的辨识上误差都最大，其中参数c的相对误差达到了9%，其余参数的误差均在5%以上，表明J-A参数辨识所使用的传统智能算法的精度不高；未改进的BES算法优于SA，同样以参数c为例，相对误差为2.5%，其余参数的相对误差基本为1%～2%左右；IBES算法辨识参数c的相对误差为0.19%，参数a的相对误差为0.25%，其余参数的相对误差也均为0.2%以下，最为精准地辨识出了各种参数。

由表3可见，SA算法耗时最长，达到了2 912 s，BES算法1 714 s，IBES算法由于需要进行精英反向学习过程，耗时稍长于BES算法，达到了1 833 s，但是达到相同的适应度值所需要的时间更短，并且最终能收敛于更优的值，实际应用中，通常不需设置这么高的迭代次数来进行参数辨识，所以时间相差会更短，如迭代20次左右，BES和IBES已到达最优解附近，时间仅相差16 s，而IBES达到了更佳的目标函数值，能避免算法陷入局部最优，综合来看，IBES算法具有更高的效率。

在实测中，测量结果常常受到仪器、人为观测误差等方面的影响，与理论曲线有一定的偏差，为了验证本文在误差影响下是否仍具有有效性，本文对噪声曲线进行参数辨识。

在曲线中加上信噪比为50 dB与70 dB的噪声，局部图如图4所示。再对曲线进行参数辨识，可得辨识结果见表4。

图4 带噪声曲线Fig.4 Curves with noise

表4 利用IBES算法辨识含噪声曲线结果Tab.4 Using IBES algorithm to identify curve containing noise

由表4可见，加噪声后辨识出的5个参数依然与原参数接近，各参数误差基本在1%以内，几乎不受噪声影响，本文方法可以正确辨识带噪声数据，这也更加证明了方法的实用性。

6 结论

智能优化算法求取J-A模型参数是常用的方法，但是传统的方法如SA、GA、粒子群优化算法存在求解速度慢、算法后期种群多样性和搜索能力均有所下降等缺陷，使得其应用起来效率不高。本文使用最新的智能算法——秃鹰搜索算法，并且在此基础上采用Tent混沌映射，自适应权重与精英反向学习，形成IBES算法，提高了BES算法的各方面性能，解决了现有智能算法求J-A模型参数易陷入局部最优、求解精度与计算效率较低的问题。为J-A磁滞模型的参数辨识提供了新方法。得到以下结论:

(1) IBES算法具有求解精度高、收敛速度快的特点，对求解 J-A 磁滞模型参数这一工程问题有较好的效果，且不受噪声影响，具有很强的实用性。

(2) 无论与传统的J-A模型参数辨识方法，还是与未改进的BES算法相比，IBES均具有更高的效率与精确度。