基于社交网络影响力的连锁故障关键线路辨识

郭 琦， 郝乾鹏， 刘 军， 孟凡成， 胡 博， 薛艳军

(1.内蒙古电力(集团)有限责任公司电力调度控制分公司， 内蒙古 呼和浩特 010020； 2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)， 重庆 400044； 3.北京清大科越股份有限公司， 北京 100084)

1 引言

近二十年来各国电网的多数大停电事故均涉及输电系统的连锁故障，例如，印度大停电事故和南澳大停电事故中均出现了线路的连锁跳闸，造成大规模电力负荷的长时间停运[1,2]。为了有效降低大停电事故风险，准确辨识电力系统的薄弱环节是非常有必要的，通过运行或规划手段来降低可能诱发连锁故障的输电元件故障率。

为有效识别电力系统的关键线路，现有研究分别从多个角度提出了输电元件的排序方法。一方面，部分文献采用电网介数等结构指标衡量元件的重要性。文献[3]通过分析电源与负荷的潮流路径构建加权电气介数，用于量化线路对系统最大输电能力的影响。文献[4]建立了潮流转移度指标，可以量化分析输电容量的安全裕度。为了进一步考虑连锁故障中的频率稳定和电压稳定，文献[5]采用动态潮流推导了线路元件的安稳影响指标。另一方面，为更全面地考虑连锁故障的传播机理，部分文献采用线路故障传播信息构建相关性网络，然后基于复杂网络理论辨识关键线路。文献[6-8]在采用潮流转移模拟连锁故障后，将故障链组合成故障网络，通过统计故障网络中各元件的出入度等网络参数辨识薄弱环节。

以上研究均为辨识连锁故障中的关键线路提供了有效思路，但在分析中没有考虑输电元件对连锁故障的重叠影响。由于调控资源有限，电网运行人员通常希望所考虑的关键线路集合能够最大化体现连锁故障的总影响。如果所辨识的关键线路对故障传播过程的影响重叠度过高，关键元件的代表性会大幅降低。为此，本文基于社交网络的最大影响力分析理论，建立了连锁故障的故障传播网络，从中选取最具影响力的关键线路集合，可更全面地代表连锁故障的风险源，为大停电风险管控提供决策参考。

2 输电线路的连锁故障模型

电力系统的连锁故障涉及到潮流转移和稳定分析等多种复杂机理[9,10]。目前，大多数的连锁故障模型在故障传播过程中主要刻画潮流转移的风险，其中由ORNL、PSerc和Alaska三个机构提出的OPA(ORNL-PSerc-Alaska)模型最为经典[11]。OPA模型的核心是从重载线路中随机抽取后续故障，模拟输电网的连锁故障。本文采用OPA模型生成连锁故障的样本集合，用于构建连锁故障的社交网络图及辨识关键线路。生成连锁故障样本的过程主要如下：

步骤1：随机模拟负荷状态，其中每个节点的负荷Di随机生成如下：

(1)

步骤2：根据随机抽样后的负荷水平，采用直流最优潮流确定系统运行状态。

步骤3：采用初始故障概率P0，随机抽取初始故障元件。

步骤4：跳开故障线路后，采用直流最优潮流更新系统运行状态。

步骤5：若出现重载线路(负载率大于阈值β)，采用故障概率P1跳开重载线路。

步骤6：若步骤5生成新的线路故障，返回步骤4；否则，至步骤7。

步骤7：输出故障事件记录，统计负荷损失。

需要说明的是，除了以OPA模型为代表的稳态机理模型外，现有研究还提出了考虑电网安全稳定的动态机理模型。由于在不同的机理模型中，输电元件的停运均是多数大停电事件的主导因素，在将停运元件划分为不同的故障阶段后，本文所提出的方法同样适用于考虑更加复杂机理的连锁故障模型。例如，进一步考虑无功特性和信息系统的影响机理后[12,13]，所提方法仍可根据样本分析故障传播影响，辨识关键线路。

3 基于社交网络影响力的关键线路辨识

3.1 连锁故障的社交网络图

为分析媒体广告、病毒等在社会群体内的传播模式，国内外学者们提出了多种社交网络的信息传播模型，如独立级联模型和线性阈值模型等[14]。独立级联模型凭借通用性较好、可解释性高等优点而被广泛采用。因此，本文采用独立级联模型构建连锁故障的社交网络图。

独立级联模型主要包括三个要素：节点、有向边和激活概率。其中，节点之间通过有向边连接，而每条边的首节点被激活后，末节点有一定概率被进一步激活。以边(u,v)为例，当节点u被激活后，节点v被已激活节点u激活的概率为p(u,v)。图1给出了一个含4个节点的独立级联模型，图中每条边上标注的数值即为激活概率。

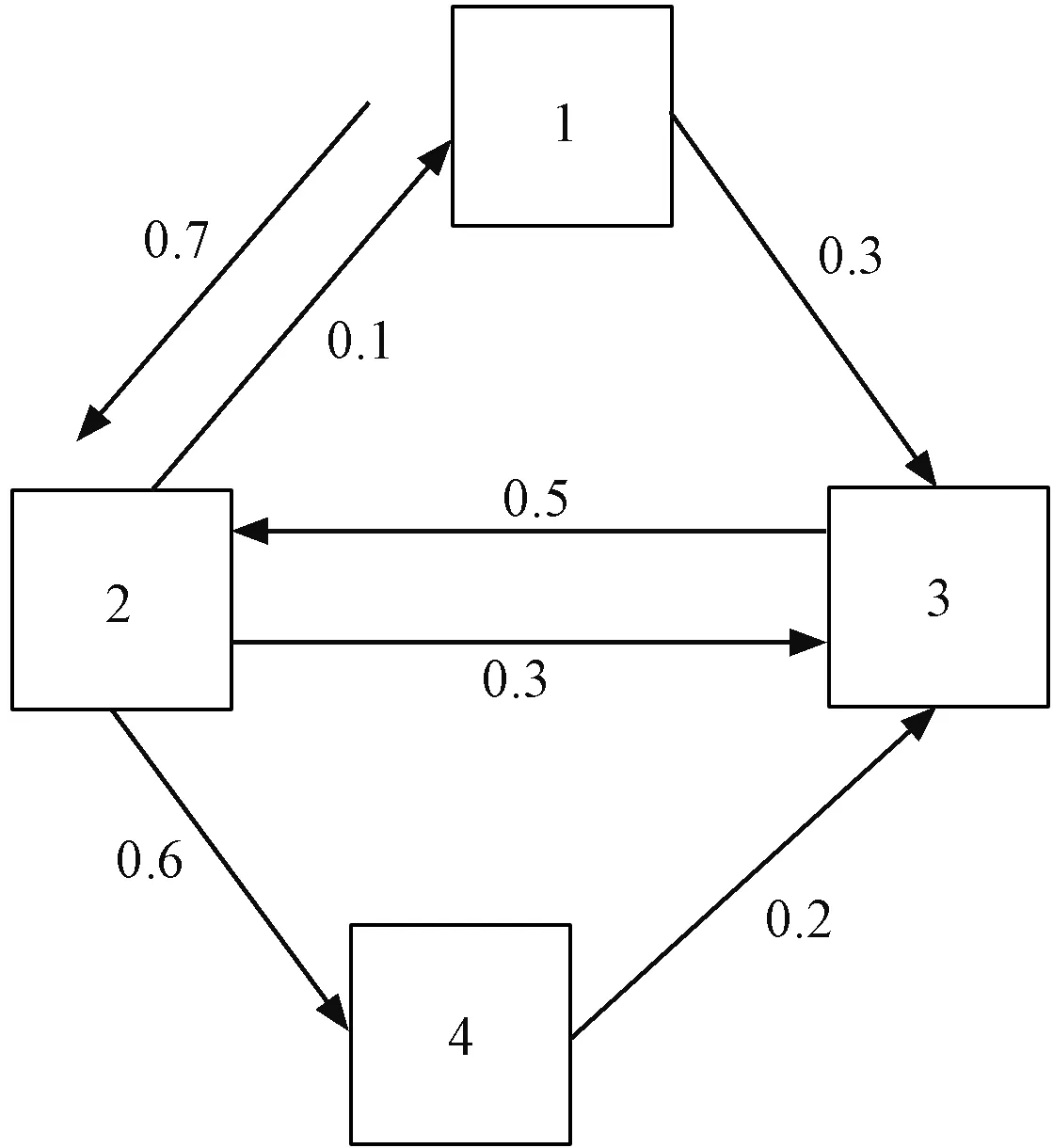
图1 独立级联模型示意Fig.1 Illustrative diagram of independent cascade model

当采用社交网络分析连锁故障的传播影响时，独立级联模型的节点对应于线路元件，而有向边则对应于连锁故障的传播方向。为了估计不同线路元件之间的故障传播概率，本文采用文献[15]的参数估计方法，从OPA模型生成的连锁故障链中，估计线路u的故障激活线路v发生故障的概率，表示为p(u,v)。在社交网络中，根据不同个体被激活的时间顺序，可将广告、病毒等媒介的传播过程划分为不同的代，并在分析传播影响时，一般假设每一代的个体仅被其上一代的个体所影响[14]。因此，本文中也根据连锁故障的传播过程将输电元件划分为不同阶段，估计前后阶段中不同元件之间的故障传播概率，具体步骤可参见文献[15]，此处不再赘述。

根据所估计的连锁故障传播概率p(u,v)，即可构建连锁故障的社交网络图，用于线路故障的影响分析。不同于文献[6]中的连锁故障图，本文的连锁故障网络并不假设故障链的每个环节仅包括1个线路故障，具有更好的通用性。

3.2 基于最大影响力的关键线路辨识

基于社交网络的影响力分析可识别信息传播的关键个体，实现最优的影响力控制，如最大化媒体广告的推广效果，或最小化病毒的传播范围[14]。类似地，为了更有效地控制连锁故障的传播，可选择在连锁故障传播网络中影响力最大的线路元件集合。因此，本节提出了一种基于最大影响力分析的关键线路辨识方法。

首先，在连锁故障传播网络中，计算线路u对线路i的影响力I(u,i)。在社交网络中，广告信息、病毒等媒质的传播概率一般均较低，所以在社交影响力的分析中多考虑二跳的情形。类似地，考虑到输电系统的连锁故障为小概率事件，故障链的发生概率随着传播长度迅速降低，因此本文综合考虑故障链的传播长度和发生概率，计算影响力I(u,i)为：

(2)

式中，ωu和ωi分别为线路u和线路i的权重系数；N为输电线路的总数量；式(2)右侧的第一项为线路i直接被线路u激活的概率；第二项为线路j受线路u影响下经二跳传播后被激活的概率。

为描述线路u对传播连锁故障的作用，可进一步定义线路u的总影响力R(u)为：

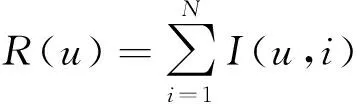
(3)

记连锁故障传播中的关键线路集合为S。在选定集合S时，若不考虑关键线路的影响力重叠效应，可采用式(4)计算集合S在连锁故障社交网络上的总影响力f(S)：

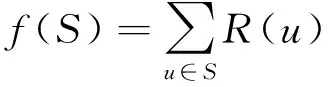
(4)

由于社交网络的最大影响力分析属于非决定性多项式(Non-deterministic Polynomial，NP)问题[14]，在选择令f(S)最大化的关键线路时，常采用贪心算法求解。具体地，首先初始化S为空集，然后采用贪心策略逐个添加线路至S，在每次选择线路时，均保证使当前S的总影响力f(S)增长量最大，即表示为：

(5)

由于式(2)～式(5)的计算过程不考虑影响力的重叠，关键线路辨识结果易出现“富人俱乐部效应”，即影响力较大的线路容易存在紧密连接，导致集合S中的关键线路可能发生聚集，使得S无法更有效地表征连锁故障的传播，进而影响故障阻断的决策效果。

为考虑连锁故障传播中线路影响的重叠性，本文提出一种新的影响力计算方法，具体如下：

首先，根据当前的关键线路集S更新线路k(k不属于S)的权重为：

(6)

式(6)表示根据当前集合S内线路的影响范围，降低线路k的权重值ωk。其含义为：当S内的线路对线路k存在较高影响时，可以通过集合S等效控制连锁故障中线路k的故障。以一种特殊情况为例，若在连锁故障样本集中线路k的所有故障均由集合S内的线路传播导致，那么根据式(6)计算的ω′k近似为0。这使得在选择新的线路时，即使线路k的故障频率很高，也不会优先考虑线路k加入S。

同时，在计算线路k对其他线路的影响时，对集合S内的线路u，更新相应的传播概率为：

p′(k,u)=(1-α)p(k,u) ∀u∈S

(7)

式中，α为取值在[0,1]的影响折扣因子。

式(7)表示当选择线路u加入集合S后，在社交网络上降低附近线路对线路u的影响能力，以保证最终选择的关键线路具有更全面的代表性。

每次选择新的线路后，分别根据式(6)和式(7)更新线路的权重系数和故障传播概率。采用贪心策略[16]重复k次以上线路选择过程，可得到对连锁故障传播影响最大的Top-k线路集合，同时大幅降低Top-k线路的影响范围重叠。

3.3 关键线路辨识算法流程

基于3.1节的社交网络和3.2节的影响力分析，即可选择电力系统连锁故障的关键线路集合。图2给出了基于社交网络影响力分析的连锁故障关键线路辨识算法流程。

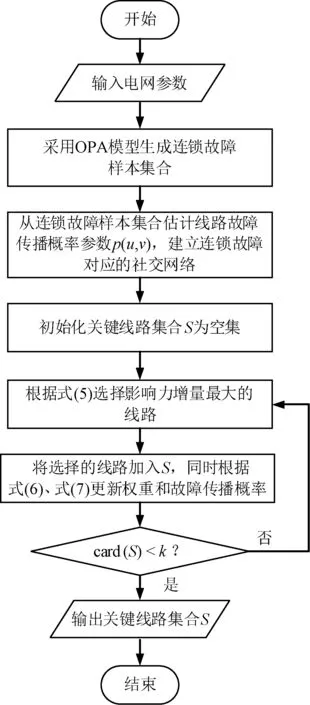
图2 基于社交网络影响力的连锁故障关键线路辨识流程Fig.2 Flow chart for critical branch identification of cascading failure based on influence analysis of social network

4 算例分析

本节采用某省级电网验证所提出算法的有效性。该省级电网共有110 kV以上线路904条。采用OPA模型生成200 000个连锁故障样本。其中，参照文献[13]，第2节中OPA模型的参数γ、β、P0和P1取值分别为2.0、0.90、0.001和0.30。在计算影响力时，所有线路的权重ω均设为1。

4.1 连锁故障的社交网络图及关键线路辨识

首先，考虑该电网的某典型运行场景A，其中负荷水平为28 862 MW，新能源出力为3 416 MW。采用连锁故障的样本集合生成连锁故障的社交网络，如图3所示。图3中，每个顶点均对应于电力系统的一个输电线路，而每一条有向边均对应于一种故障传播链接，即在该有向边的首端顶点故障后，末端顶点发生连锁故障。

图3 某实际电网连锁故障的社交网络Fig.3 Social network for cascading failure of actual grid

从图3中可见，尽管连锁故障涉及到大量的线路，只有少量线路处于社交网络的中心，对连锁故障的传播起关键作用。分别采用以下4种方法辨识连锁故障的关键线路集合：

方法1：考虑不同线路的影响重叠性，采用所提方法辨识影响力排序前20的关键线路，其中折扣因子设为0。

方法2：不考虑不同线路的影响重叠性，采用所提方法辨识影响力排序前20的关键线路。

方法3：参考文献[6]，以激活概率p(u,v)为权重，采用加权出度选取排序前20的关键线路，即易影响周边元件的关键线路。

方法4：参考文献[6]，同样以激活概率p(u,v)为权重，采用加权入度选取排序前20的关键线路，即易受周边元件影响的关键线路。表1对比了不同方法辨识的关键影响线路。

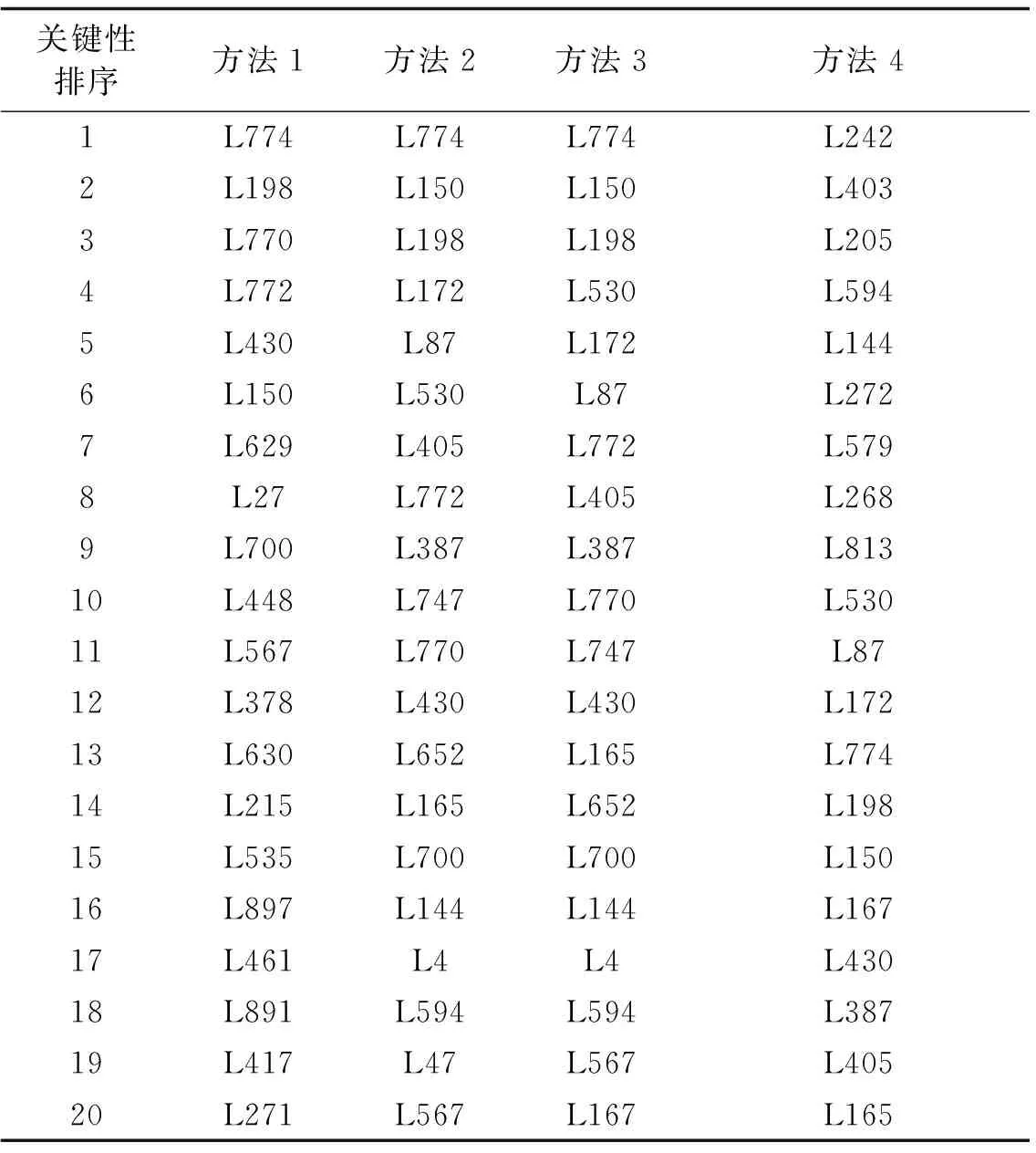
表1 关键线路辨识结果对比Tab.1 Comparison of identified critical branches

从表1中可见，在所辨识的关键线路中，方法2和方法3的重合度较高，且结果与方法4差异较大。这是因为方法2和方法3均主要量化线路对其他输电元件的故障影响，而方法4主要辨识易受其他元件影响的关键线路。另一方面，虽然方法1也量化线路对其他元件的故障影响，但由于计及了线路影响的重叠，方法1的影响力排序相较于方法2发生明显变化。

为了对比方法1和方法2的结果差异，图4和图5分别给出了所辨识关键线路在图3所示的社交网络上的连接关系。

图5 方法2所辨识关键线路在社交网络上的连接关系Fig.5 Connection of critical branched identified by method 2 on social network

对比图4和图5的网络连接关系可以发现，方法1所辨识关键线路之间的耦合关系相对稀疏。其中，连接到图4的每个节点的平均边数为3.10，而图5则为9.95。结果表示：方法2的辨识结果中存在明显的“富人俱乐部效应”，即由于紧密连接关系的存在，激活图5中所有节点所要求的故障数量远低于图4。同时，图4中线路L417、L535和L629与其他17条关键线路之间不存在连接关系，这表明在故障传播中，其余17条线路的故障对这3条线路产生的影响较小。

以方法1中排序前20的关键线路为例，图6对比了考虑重叠性前后的关键线路影响力。从图6中可见，计及影响重叠效应时，排序靠后的线路影响力有所降低，且降低幅度差异较大。例如，若不计及重叠性，线路L150的影响力排序为第2，但由于L150与排序第1的L774的影响范围重叠度较高，在计及L774后L150的重要程度会有较明显的降幅，线路L198的关键性会超过线路L150。

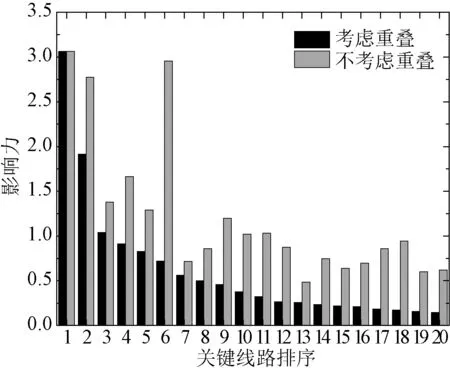
图6 考虑影响重叠性前后的关键线路影响力对比Fig.6 Comparison of influence of critical branches before and after consideration of influence overlapping

最后，为验证所辨识关键线路的有效性，依次选取前k(k=1，2,…，20)个关键线路作为连锁故障的初始故障，模拟连锁故障的传播情况。对每个初始故障集，均模拟1 000次连锁故障，并统计平均线路停运数量作为影响力衡量指标。图7给出了对应的平均线路停运数量结果。

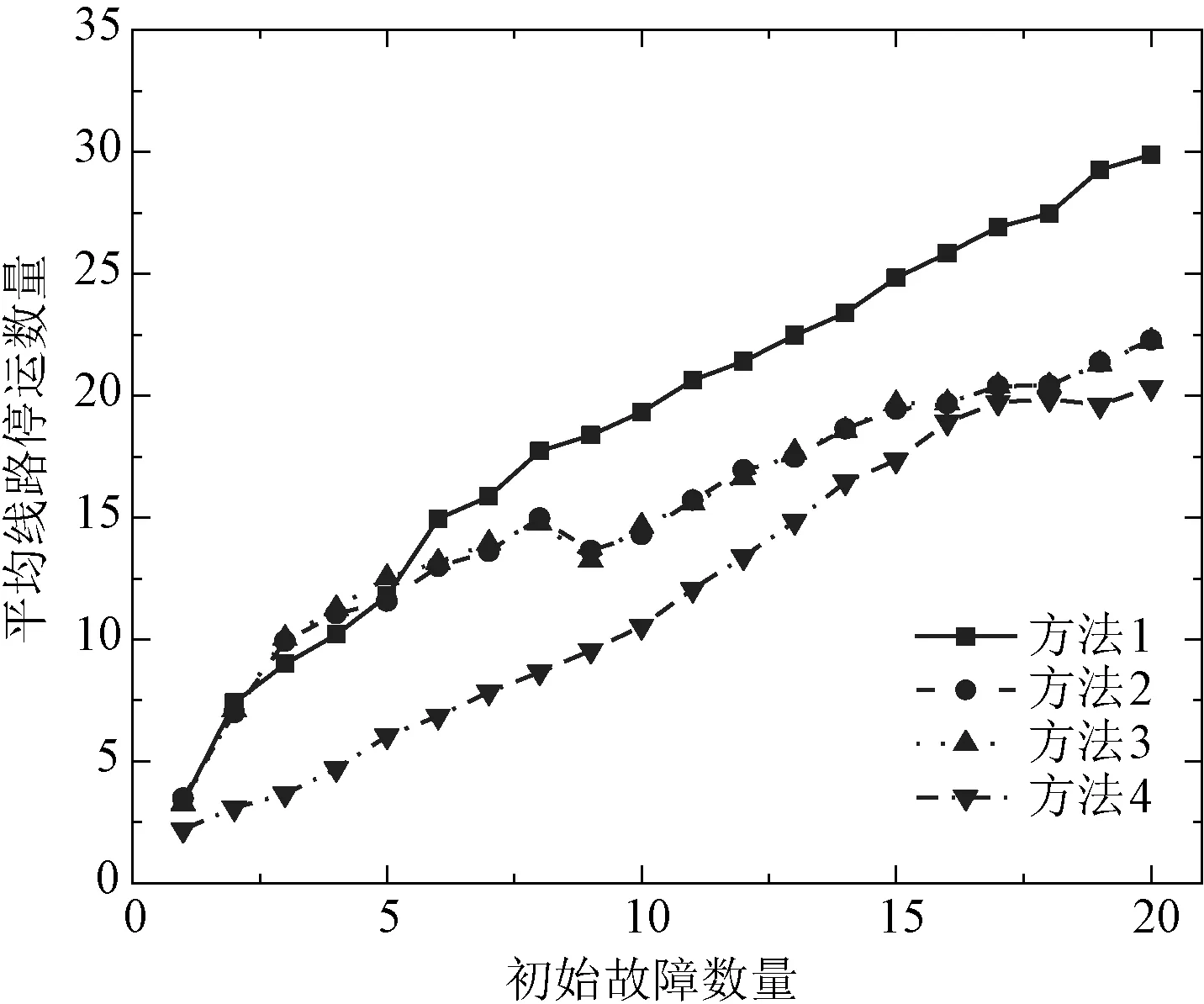
图7 关键线路作为初始故障引起的平均线路停运数量Fig.7 Average number of branch outages with critical branches as initial outages

从图7中可见，当初始故障选择的关键线路数量较少时，方法1、方法2和方法3所诱发连锁故障的数量比较接近，均高于方法4诱发的线路停运数。这是因为方法4识别的线路更易受其他故障影响，而非诱发新的线路停运。但是，当初始故障数量大于10以后，所提方法诱发的线路停运数量明显高于其余方法。特别地，当初始故障数量为20时，方法2和方法3所引起线路停运总数也接近20，而方法1则为30。这表明由于“富人俱乐部效应”的存在，方法2和方法3的关键线路构成紧密联系，这些线路内部存在较高的故障传播概率，仅部分线路故障即可激活这些关键线路，但是对系统内其余线路的影响则并非最大。方法1考虑了影响重叠性对关键线路辨识的遮蔽效应，可更全面地辨识连锁故障传播网络的关键线路集合。

4.2 影响折扣因子的灵敏度分析

为分析影响折扣因子α对关键线路辨识结果的影响，分别将α设为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1.0。在不同的折扣因子取值下，依次辨识关键线路，并按照4.1节的方法验证所辨识关键线路的有效性。将以上11个场景依次记录为场景1～场景11。另外，为了说明式(6)更新线路影响权重对关键线路辨识的影响，在折扣因子α设为1.0的前提下，去除式(6)的计算过程，并将其记为场景12。

图8中对比了结果中对应的平均线路停运数量。从图8可见，当考虑α取不同值的时候，由于场景1～场景11均采用式(6)更新了线路权重，各个场景下诱发的连锁故障数量较为接近，而且α取较大的折扣系数时连锁故障数量更加稳定。这是因为在更新线路权重后，场景1～场景11所辨识的线路集合重合度很大，主要体现为线路之间的相对排序发生小幅换位。

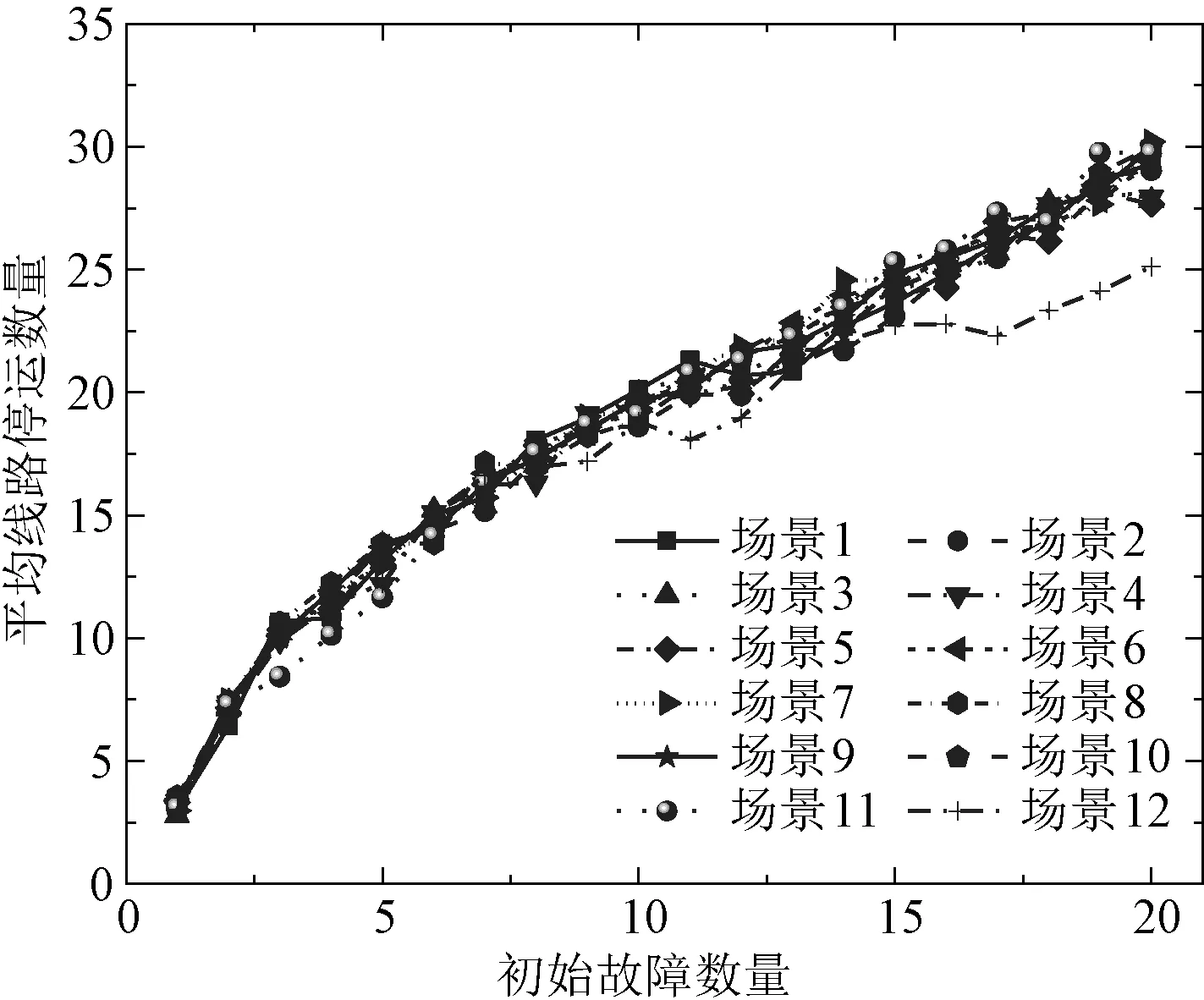
图8 不同折扣因子下平均线路停运数量Fig.8 Average number of branch outages under different discount factors

进一步结合场景12的结果可以发现，如果不考虑式(6)对线路影响权重的更新，最后的连锁故障数量明显低于场景11。同时，场景1～场景12中所有的连锁故障数量均高于图7中不考虑影响重叠性的情形。这表明所提出的线路影响量化策略可以有效地提升薄弱环节的辨识效果。

4.3 多运行场景下的电网关键线路辨识分析

为分析新能源渗透率、负荷水平等典型运行场景差异的影响，除了4.1节中的运行场景A外，考虑另外两个典型场景B和场景C。其中，场景B和场景C的负荷水平分别为24 828 MW和29 506 MW，新能源出力水平则分别为2 273 MW和10 560 MW。

对场景A、场景B、场景C分别生成连锁故障样本后，在α设为0的前提下，依次辨识关键线路集合。图9中对比了不同运行场景下关键线路诱发的平均线路停运数量。

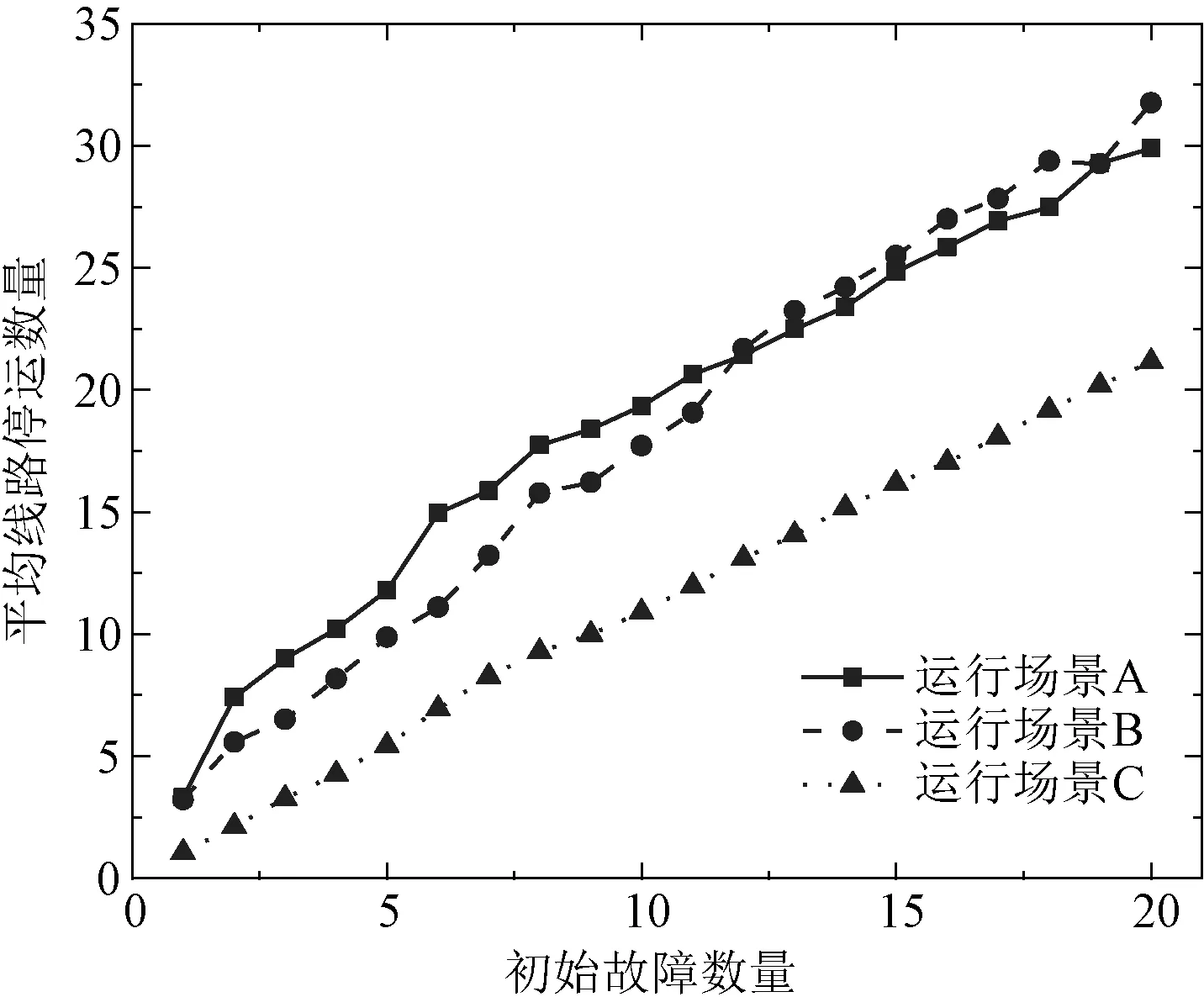
图9 不同运行场景下平均线路停运数量Fig.9 Average number of branch outages under different operation scenarios

由图9可见，三个运行场景下发生连锁故障的风险明显不同。这是由于关键线路的辨识不仅由电网的电气结构决定，还与电网的实时运行状态相关。特别地，场景C中平均线路停运数量分布的斜率近似为1，即对应的初始故障未诱发新的连锁故障。这是因为尽管场景C的负荷水平最高，但新能源处于大发状态，系统可调度电源充裕度明显高于场景A和场景B，而在OPA模型中，每次故障后调度全网机组实现功率再平衡，因此场景C的输电网潮流分布更均匀，降低了连锁故障风险。此外，场景A和场景B的新能源出力接近，但场景A下的负荷水平高于场景B，因此多数情况下场景A的连锁故障风险高于场景B。

5 结论

为有效分析输电系统连锁故障的传播特性，本文基于社交网络理论建立了连锁故障的传播网络，通过计及重叠效应的社交网络影响力分析，提出了一种关键线路辨识方法。以某实际电网为例，基于OPA模型的连锁故障样本建立连锁故障传播网络，关键线路的辨识结果表明：在连锁故障的传播过程中，仅少量的线路对故障传播存在支配性影响；在考虑不同关键线路影响的重叠性后，所提方法可以更全面地表征故障的传播模式，有效降低“富人俱乐部效应”导致的遮蔽效应。

下一步研究将考虑建立多样化的折扣指标和更复杂的连锁故障机理，在连锁故障关键线路辨识中更全面地刻画输电元件的影响力。